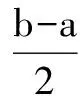高考中常见的对称问题

叶 炼

(广东省鹤山市第一中学,广东 江门 529700)

高考中常见的对称问题

叶 炼

(广东省鹤山市第一中学,广东 江门 529700)

笔者结合高考题就点关于直线l对称、曲(直)线关于直线l对称、曲(直)线关于y轴的对称、曲(直)线关于y=x轴的对称、曲(直)线关于y=-x轴的对称、曲线关于一般直线Ax+By+C=0对称、函数图象本身的对称问题以及函数间的图象对称问题，进行了案例分析解析.

高中数学 对称问题 案例解析

对称问题是中学数学的重要内容之一，也是高考的热点内容.本文结合高考题，阐明常见对称问题的解法.

一、关于直线对称

1.点关于直线对称

例1 原点关于直线8x+6y=25的对称点坐标为( )

2.曲(直)线关于直线l对称

(1)曲(直)线关于x轴的对称

例2 . 和直线3x-4y+5=0关于x轴对称的直线方程为 ( )

A.3x+4y-5=0 B.3x+4y+5=0

C.-3x+4y-5=0 D. -3x+4y+5=0

分析 由曲线f(x,y)=0关于x轴的对称曲线为f(x,-y)=0知：将原方程的y换成 -y即答案B.

(2)曲(直)线关于y轴的对称

例3 如果l与直线x+y-1=0关于y轴对称，那么直线l的方程是

分析 由曲线f(x,y)=0 关于y轴的对称曲线为f(-x,y)=0知：将原方程的x换成-x得-x+y-1=0，即x-y+1=0.

3.曲(直)线关于y=x轴的对称

例4 已知直线l1、l2的夹角的平分线为y=x，如果l1的方程为ax+by+c=0(ab>0)，那么l2的方程为( )

A.bx+ay+c=0 B.ax-by+c=0

C.bx+ay-c=0 D.bx-ay+c=0

分析 此题实质是求：l1关于直线y=x的对称直线.

由曲线f(x,y)=0关于直线y=x的对称曲线为f(y,x)=0知:将原方程的x和y对换即得答案A.

4.曲(直)线关于y=-x轴的对称

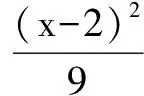
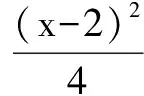
再整理即选A.

5.曲线关于一般直线Ax+By+C=0对称

求已知曲线C1关于直线l的对称曲线C2的方程，在C2上任取一点P(x,y)，可求出它关于l的对称点坐标，再代入C1中，就可求得C2的方程.

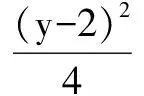
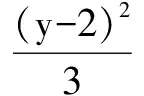
二、函数图象本身的对称问题

例7 如果函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t)，那么( ).

A.f(2)

C.f(2)

三、函数间的图象对称问题

例8 设函数y=f(x)定义在实数集上，则函数y=f(x-1)与y=f(1-x)的图象关于( ).

A.直线y=0对称 B.直线x=0对称

C.直线y=1对称 D.直线x=1对称

综上所述，求对称问题这里仅仅列举的几例，在平时的教学中，我们要举一反三，有重点地进行针对性的训练.只有善于观察，勤于思考，不断总结经验，才能达到熟能生巧的程度.

[1]叶炼.高考对称问题八例[N].广东招生报.2003，1.

[2]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2013.

[3]夏钰钦.实现数学课堂教学有效性的五大要领[J].课程·教材·教法，2012(8):38-42.

[责任编辑：杨惠民]

2017-05-01

叶炼(1968-)，男，汉族，广东阳江人，中学高级教师，硕士学历，研究方向：数学教学.

G632

B

1008-0333(2017)19-0053-02