浅谈几类数学思想在高考中的运用

王恩泽

(华中师范大学第一附属中学高三(21班)，湖北 武汉 430000)

浅谈几类数学思想在高考中的运用

王恩泽

(华中师范大学第一附属中学高三(21班)，湖北 武汉 430000)

本文重点总结了我们在高中数学学习过程中比较重要的，也是各种考试中容易考到的几类典型的数学思想，并以具体的例题展示了在解题过程中如何灵活运用这些思想，希望通过本文的总结，能对我们数学解题能力的提升有所帮助.

高中数学；数形结合；函数与方程；转化与化归；分类与整合

高考着重于专题知识点的巧妙结合与对数学技巧、思想方法、数学运算能力的考查，同时也考核了学生对基础知识的精准理解以及综合运用.在高中数学学科的学习与复习中，同学们应该在整体把握各部分基础知识的同时，优化思维、求同存异、知一反三，全面提升自身的数学学习、认知和考试能力，而数学的精髓所在即是数学思想的提炼和技巧的整合．在此我和大家一起分享以下几种常见的数学技巧与方法：

一、数形结合在于“数”与“形”的桥梁搭建

“数”与“形”是最古老的数学形式，也是数学学习中最重要的两块基石.“数” 具有严密性和抽象性，而“形”则具有直观性和表达性，由“数”解“形”和以“形”助“数”是数形结合最基础的运用.

1. 以数解形

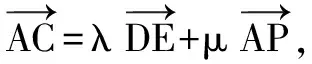
分析 可通过建立直角坐标系引入三角函数，化“形”为“数” 进而技巧运算.

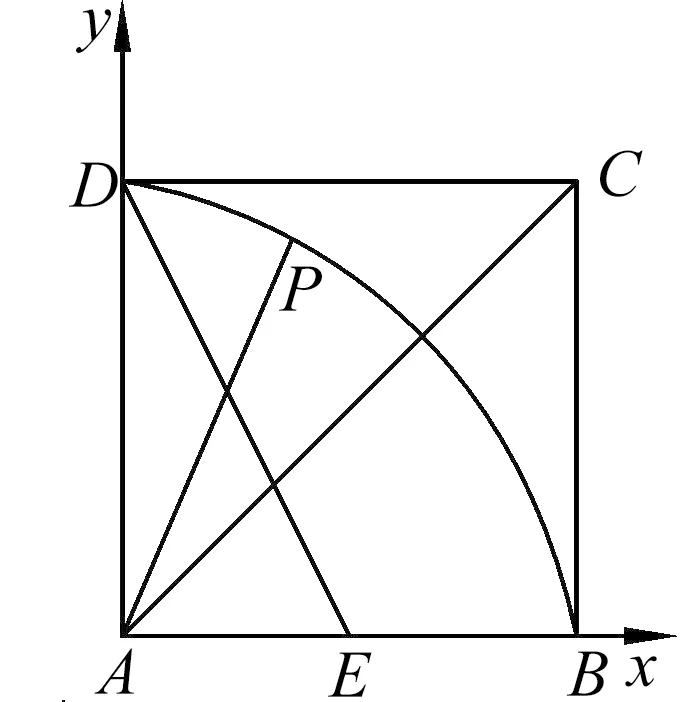
解 以A为坐标原点，以AB，AD为x轴和y轴的非负半轴，建立如图所示的直角坐标系.

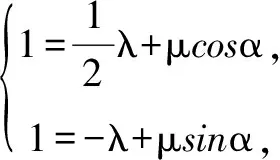
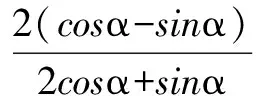
2.以形助数

例2 若实数a,b,c,d满足(b+a2-3lna)2+(c+d+4)2=0，则(a-c)2+(b-d)2的最小值为______.

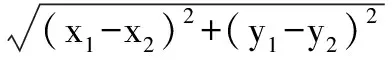
解 因为(b+a2-lna)2+(c-d+4)2=0，

所以b=3lna-a2,

①

且d=c+4.

②

将①②转换为两个函数表达式，即y=3lnx-x2,

③

y=x+4.

④

记③为C1曲线，同时记④为C2直线，那么这个时候，我们可以构造成“形”的问题，即在C1和C2上存在两动点，这两动点距离的最小值即我们题目要求的备案，而此时的两动点，可再次转换为将C2平移至与C1相切，求出切点到C2的距离：

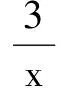
二、函数与方程思想

函数是运动和变化的，方程是静止和确定的.所谓函数与方程思想即是化“动”为静，变“静”为“动”，“静”难则“动”易.两者相辅而成，重点在于研究“动静”之间的数量关系.

1.函数思想的运用

例3 在等差数列中，已知ap=q且aq=p，p≠q，求ap+p.

分析 关于等差数列中an的通项公式可记为an=An+B(其中A不为0)，我们可以把an理解为一个一次函数表达式.

解 记an=An+B为f(n)=An+B，因为ap=q，且aq=p，即(p,q),(q,p)两点在f(n)=An+B的图象上，此时有

q=pA+B,

①

p=qA+B.

②

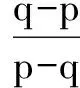
所以ap+q=0.

2.方程思想的运用

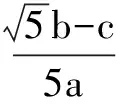
三、分类与整合思想用于解含参数类题型

“分而拾之，各个击破”是分类与整合思想的核心，我们常常把一个带有参数的数学问题按照题设中已有(或隐含条件)数据进行有条理的讨论，分析与计算，从而一步步接近答案，解决这一整个题目.

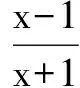
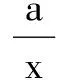
(Ⅰ)当a≥0时，f(x)>0恒成立，f(x)在(0,+∞)上为单调递增；

四、转化与化归思想让题目简单化

化难为易是转化与化归的最终目的.一般地，我们通过转化和化归的方式将困难和陌生的问题化为简单和熟悉的问题，往往题设中会有以前见过的“影子”知识点，所以转化与化归思想的第一步是快速找到转化点.

例6 设不等式2x-1>m(x2-1)对满足|m|≤2的一切实数m都成立，求实数x的取值范围.

分析 二次函数的参数问题，所以换元是解该题的重点所在.

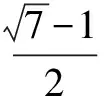
从以上看来，我们已经看到了数学思想解题的重要性，它不仅仅涉及某个题，并且在学习过程中也能很好的启迪思维，所以掌握好数学里的几类数学思想，用思想指导解题，往往可以起到事半功倍的效果.

[1]杨永海.高考数学复习的方法和技巧[J].数理化学习(教育理论版),2010(01):11-12.

[2]盛军.数形结合方法在高中数学教学中的应用评价[J].赤字(上中旬),2016(08).

[责任编辑：杨惠民]

2017-05-01

王恩泽(1998.10-)，男，湖北武汉人，高中在读.

G632

B

1008-0333(2017)19-0013-03