尝试分析典型古建筑构件—斗拱的力学原理

2017-09-03黄宇扬

数理化解题研究 2017年19期

关键词：斗拱泰安力学

黄宇扬

(山东省泰安英雄山中学高一16班，山东泰安 271000)

尝试分析典型古建筑构件—斗拱的力学原理

黄宇扬

(山东省泰安英雄山中学高一16班，山东泰安 271000)

斗拱是最能代表中国古代建筑艺术的构件.本文通过查找相关资料，请教专业技术人员，建立了简单的斗拱模型，分析了斗拱的力学原理，明确了斗拱的承重功能.并提出应在现代建筑的设计中充分借鉴中国古代建筑智慧，建造出更多独具中国特色的建筑.

斗拱;梁、荷载;模型

一、论题的由来

在我很小的时候，父母就经常带我在祖国各地游览，参观当地古老的建筑，熟悉当地的民俗文化.北京城内气势恢宏的故宫、曲阜书香氛围浓厚的孔庙、开封城内肃穆严明的开封府、大理古城中壮丽又不失精致的崇圣寺以及藏区“圣地”大昭寺，这些在悠久的岁月长河中沉淀下来的古老建筑无一不散发着一种古朴典雅的气息，吸引着我的目光，而渐渐地我也发现，在这些古建筑的华美壮丽之下，斗拱总是不可或缺的.本以为斗拱只是带有民族特色的装饰罢了，可父亲却告诉我斗拱是古代建筑中的重要构件，担负着荷载与抗震的作用.这个答案很意外，也引发了我的好奇心，不大又显得有些脆弱的斗拱是如何支撑起整个屋顶的呢？这其中又隐含了哪些我所不知道的知识呢？

二、研究方法和思路

明确研究主题——查阅相关资料——利用软件建立模型——进行力学分析——得出结论

三、关于斗拱的结构

图1 古建筑中斗拱图样

斗拱是中国古代建筑中特有的一种结构，它位于古代建筑的柱顶、房檐间，具有不同的形式.主要由“拱”和“斗”组成，拱是从枋上向外延伸的一层层成弓形的承重结构，斗是拱与拱之间连接的方形木块，后来随着发展又增加了升、翘、昂等构件，如图1.据史书和出图的碑刻上记载，最早的斗拱出现在西周至南北朝，至唐朝应用最为广泛，也被当时的皇权政府规定民间不得使用.到明清以后不再起到维持构架整体性和增加出檐的作用，用料和尺度比宋式有很大缩小.斗拱是最能代表中国古代建筑艺术的构件，中国建筑学会的会徽上就是一个抽象的斗拱图案.

四、建立斗拱的简单模型

未来对斗拱的结构有更直观的感受，笔者试着对典型斗拱模型进行了安装，如图2.

图2 笔者拼接斗拱模型

由于笔者为高中学生，所学物理知识有限，因此在分析斗拱的受力结构时请教了结构专业的专家，选取的是最简单的模型和力学分析，建立的模型为立柱直接承载梁和只有一层的斗拱承载梁，通过对两种模型中的横梁两端施加相同的载荷，比较出对横梁的尺寸要求.通过控制横梁尺寸相同，比较两种模型中横梁所能承受的最大载荷，如图3、图4.

图3 立柱直接承载梁模型图4 一层的斗拱承载梁模型

五、分析斗拱的力学原理

这里我们通过控制梁两端所加载荷相同比较对梁的尺寸要求、控制尺寸相同比较最大载荷两个方面来比较.

1.模型计算中用到的尺寸和常量

梁和斗拱选用木材的杨氏模量：E=12.5Gpa

梁和斗拱选用木材的许用应力：[σ]=10Mpa

梁和斗拱选用木材的密度大小：ρ=0.5×103kg/m3

重力加速度：g=10.0kg·m/s2

2.常用基本量

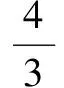
由梁自重带来的均匀载荷分布：g=bhg=gb2⑵

3.两对称支点支承梁的模型的计算分析

模型如图5所示.计算得：

梁的弯矩方程：

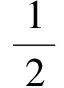
图5 梁模型

梁的弯矩图：

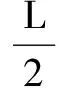
以a为常数，L为变量讨论得：

1)当a、L的关系满足：

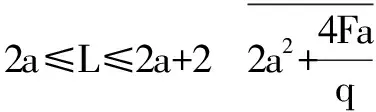
弯矩绝对值的最大值为：

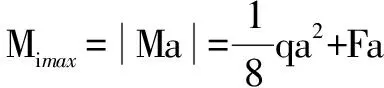
2)当a、L的关系满足：

弯矩绝对值的最大值为：

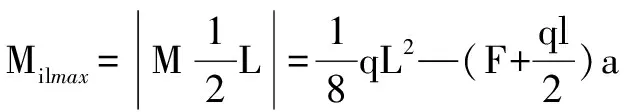
4.仅用立柱承载梁的情形

如图2所示，令：L=2.00m，b=7.00cm；梁两端加载载荷Fp=1.0KN.(8)

计算：梁截面惯性矩：

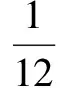
梁自重的均匀载荷分布：q=32.67N/m；

弯矩绝对值最大处是立柱支承处：

则梁中最大正应力绝对值为：

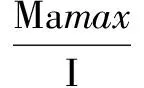
5.只有一层的斗拱承载梁的情形，如图6

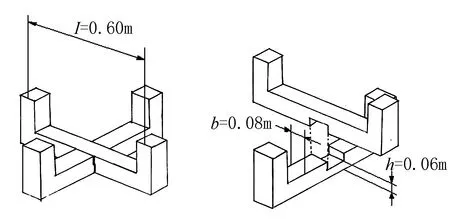
图6 只有一层的斗拱承载梁模型

对斗拱计算：

弯矩方程：Mx=-Fx

得出弯矩绝对值最大处：

最大弯矩处斗拱正应力绝对值最大值：

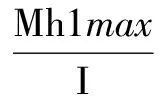
去除量纲，求出以载荷F为变量的数值解：

Mh1max=0.3F；σv=208.3F；σh1=6250F(12)

考虑许用应力[σ]=10MPa，则求出F的最大值：Fh1max=1.6KN (13)

对斗拱承载的梁计算：

a、令梁两端载荷大小一定，梁宽b为变量：

L=2.00m；梁两端加载载荷；

当梁对称摆放时，a=0.70m

计算最大弯矩处的最大正应力：

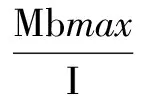
将各量去除量纲并代入数据，利用关系：σbmaxσ得到：

107b3-5512.5b2-3307.50(15)

解出唯一可行解：b0.06934(16)

这时，斗拱两垫木分别承担的载荷大小为：

b、令梁宽b大小一定，梁两端承载载荷大小为变量：

L=2.00m；梁宽b=0.060m；当梁对称摆放时，a=0.70m

利用⑷、⑹两式对L和a的值进行检验得：弯矩绝对值的最大值在x=a处取到，大小如⑸式所示，即：

计算最大弯矩处的最大正应力：

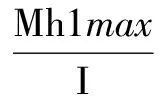
代入数据，利用关系：σbmaxσ

得到：Fp0.91KN

这时，斗拱两垫木分别承担的载荷大小为：

六、结论

通过专业人员的技术分析，我们可以看出：在梁的尺寸相同的情况下，使用斗拱可以使梁两端可承受载荷的大小明显增加.斗栱不但具有装饰功能，同时具有很重要的承重功能，它在中国古代建筑中起着承上启下，传递荷载的作用.它是古代人民在建设中不断摸索出来的智慧的体现.

七、现实意义

类似斗拱的建筑构件不但能用在中国古代建筑中，对现代建筑设计也具有很强的借鉴作用.在现代建筑设计中可以利用古代建筑构件和符号体现出民族性、传统性，也可以借鉴传统建筑构件作出现代建筑结构，如获得被誉为建筑学界诺贝尔奖——普利兹克奖的王澍设计的中央美院象山校区的建筑就用了斗拱结构，成为了建筑界不朽的经典，如图7.