等效思维在高中物理解题中的应用

李 娜

(山东省肥城市第一高级中学2015级21班,山东 肥城 271600)

等效思维在高中物理解题中的应用

李 娜

(山东省肥城市第一高级中学2015级21班,山东 肥城 271600)

等效思维就是将某些繁杂抽象的问题等效成一些简单、形象的问题来进行求解，它涵盖了等效变换、等效替代、等效假设、等效类比等.求解问题是能达到事半功倍的效果.

等效思维；变换；替代；假设；类比

等效思维本身是一种科学的思维方法，其可以将某些繁杂、抽象的问题等效成一些简单、形象的问题来进行求解，同时也有助于强化学生对于某些物理知识、规律和原理等的记忆，尤其适用于电学、动力学以及力学等物理类型题目的求解中.本文基于等效思维，探讨了其在高中物理解题中的具体应用.

一、巧用等效思维，进行等效变换

等效变换就是通过借助等效思想来变换某些问题中的条件、添加图线、添加一对平衡力、变换图形或者参数等来达到简化问题的目的.比如，将那些比较繁杂的电路等效变换成一些具有明显串并联关系的电路.简言之，等效变换就是在不破坏问题“本质”的基础上，将相关的问题变成一些高中生比较熟悉的物理问题模型，借此来简化相关计算题，降低解题难度.

例1 已知共点的三个分力F1、F2和F3之间互成120°(图1(1))，且三者的大小依次为20N、30N和40N，试求三者合力大小及方向？

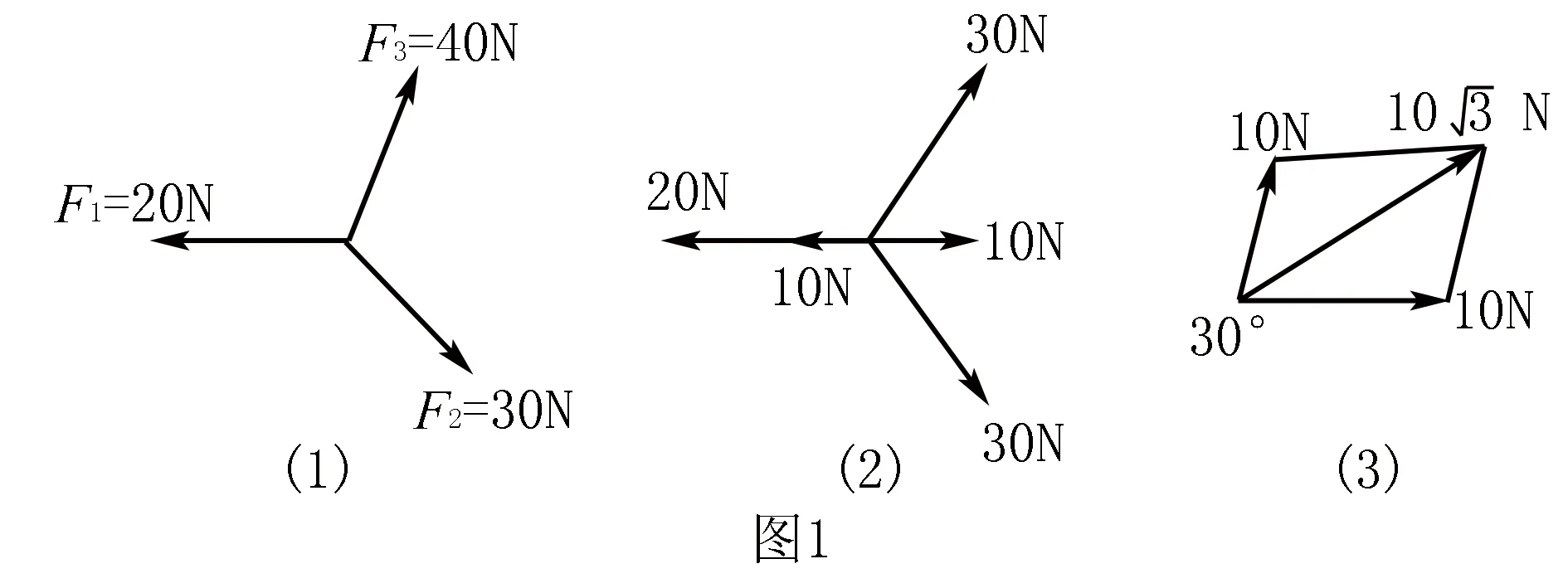
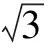
二、巧用等效思维，进行等效替代

等效替代也是等效思维方法中常见的一种形式，其主要是不破坏问题本质的基础上，采用替代法来将问题题干中的某部分或者某个组合来进行替换，借此来达到简化和解决复杂物理问题.但是需要注意的是在运用该法进行问题求解期间，必须要注意结合物理问题的实际情况来确定替代内容，避免违反问题的本质，否则很容易影响解题的准确度.

例2 如下图2，已知等臂杠杆AB两端配置有同种类材料构成的圆板，A段固定圆板半径为R，在其上部挖一个半径为R/2的r，已知OA=2R，试求保持杠杆平衡状态下B端圆板的半径值？

解析 如果按照常规的解题思路进行求解，那么需要先求解出A端圆板重心位置所在，但是这种计算方法比较繁琐，难度比较大，此时如果可以采用等效替代法，那么可以有效地简化计算流程，提高解题效率.考虑到A端圆板本身上挖有一个圆孔，此时可以假设没有挖孔，假设该部分出作用有一个大小等于挖取部分重力F作用于孔心C位置处，此时再继续按照传统方法进行求解即可达到快速解决问题的目的，具体等效替换之后的问题求解如下图3所示.

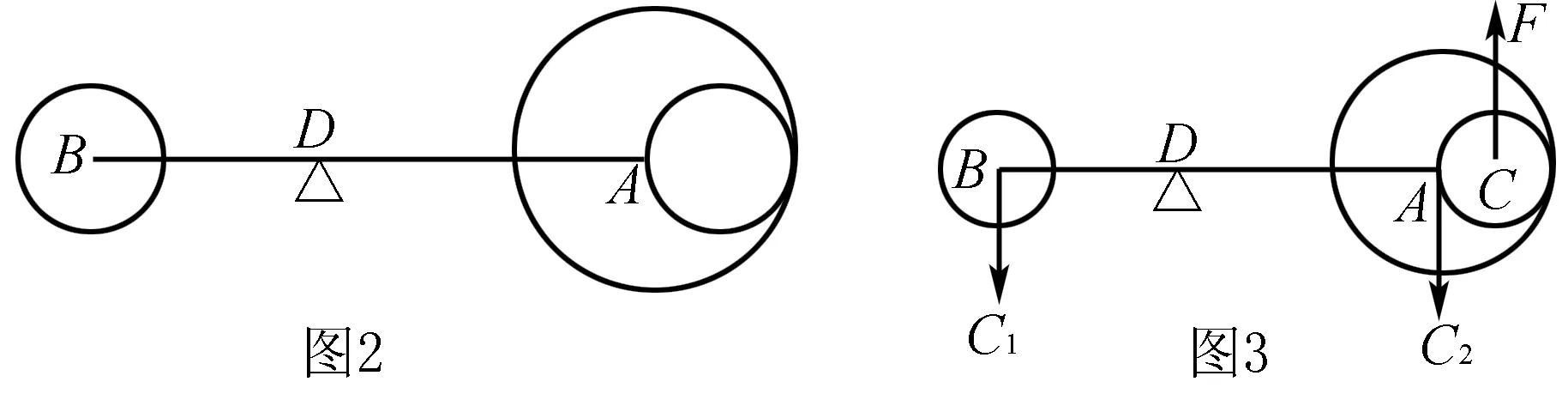
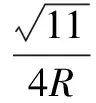
三、巧用等效思维，进行等效假设

所谓的等效假设实际上就是基于效果统一性，显著凸显出某些问题的隐含条件，借此来达到简化繁杂问题，快速求解物理问题的目的.该种等效思维的的重点在于“化隐为明”，将那些潜在的问题条件挖掘出来，确保解题期间可以有充足的解题条件.

例3 如图4所示电路图，电源电动势、内电阻、定值电阻、变阻器分别为ε、r、R1和R2，试求变阻器消耗的电功率最大值为？

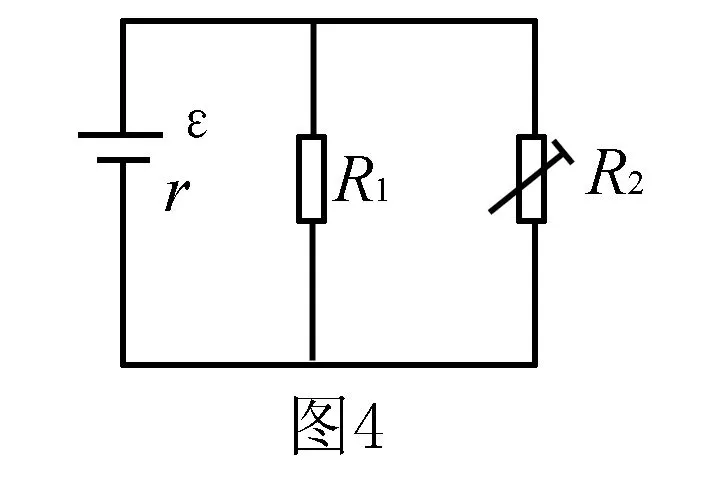
四、巧用等效思维，进行等效类比

除了上述几种等效思维思想之外，等效类比也是比较常见的一种等效思维思想和方法，其主要是通过类比的方式来扩展解题思路，比如可以通过类比以往与相关问题求解类似的具体求解过程来达到求解问题，是一种非常实用的问题求解方法.

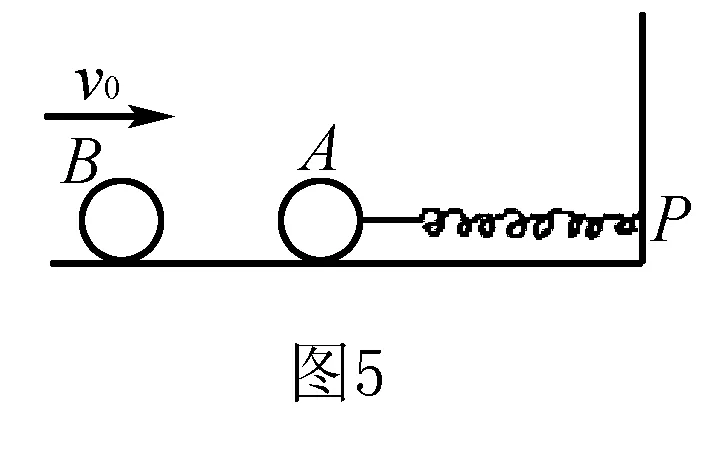
例4 如图5所示，已知在一端P点固定有强度系数为K的轻质弹簧，另一端连接有质量为m的A球，B球(m)以V0的速度和A球发生碰撞，之后二者共同在光滑面上进行滑动，之后又继续做一往回运动，试求A球和B球相互脱离时刻所持续的时间？

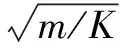
综上所述，等效思维在高中物理解题中的应用包含了诸多方面，涵盖了等效变换、等效替代、等效假设和等效类比等等，但是实际的应用本质均是要在不违背“等效”原则的基础上来对原有条件或者等式进行变换，借此来达到简化问题的目的，所以在实际的解题中必须要重视等效思维应用时刻的等效条件是否满足，确保可以借助等效思维来解决高中物理问题.

[1]李宝银.高中物理“探索在前,教材在后”的教学实践[J].教育理论与实践，2010(20).

[2]陈永建.提高高中物理实效性教学策略探究[J].科技资讯,2012(35).

[责任编辑：闫久毅]

2017-06-01

李娜(1999-)，女，山东人，爱好广泛，擅长数学和英语学习.

G632

B

1008-0333(2017)19-0086-02