例谈向量在立体几何中的应用

曾石明

(江西省赣州市于都中学，江西 赣州 342300)

例谈向量在立体几何中的应用

曾石明

(江西省赣州市于都中学，江西 赣州 342300)

立体几何是高中数学中重要的组成部分，高中的立体几何主要是学习在三维空间中空间图形的形状以及大小.线线位置关系，线面位置大小关系，点线位置及其距离关系，面面距离位置关系.而空间向量是将抽象的立体几何转化成了函数，代数的数量关系.以下内容主要是对于向量在立体几何的一些主要类型的实际应用进行论述.

向量；立体几何；位置关系

一、向量求点线位置关系

公式 点M(x0，y0)到直线l：Ax+By+C=0的距离

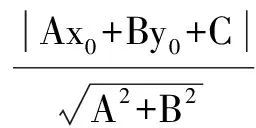
例1 经过点A(-1，2)，且平行于向量a=(3，2)的直线方程是________．

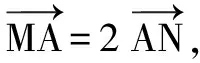
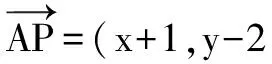
(2)设N(x，y)，M(x0，y0)．

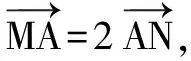
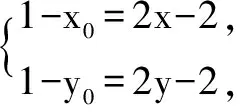
所以(x0-3)2+(y0-3)2=4，所以(2x)2+(2y)2=4，即x2+y2=1.所以点N的轨迹方程为x2+y2=1.

二、向量求点面位置关系

利用向量法求空间距离问题是空间向量的重要应用，也是立体几何的重要考点.我们解决这类问题时，可选取恰当的空间直角坐标系，把所需线转化为相应向量.

主要步骤如下：

(1)建立空间直角坐标系;(2)求平面的一个法向量的坐标；(3)找出平面外的点与平面内任意一点连接向量的坐标;(4)代入公式求出距离.

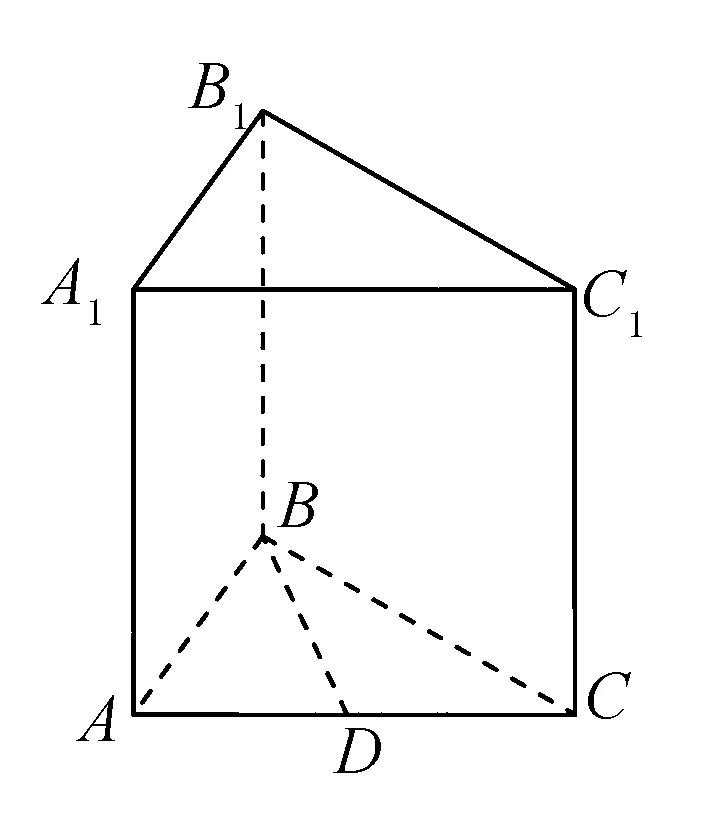
例2 在直三棱柱ABC-A1B1C1中AB=BC=5,AC=8,AA1=6，D为AB的中点.

求：点B到面AB1C的距离.

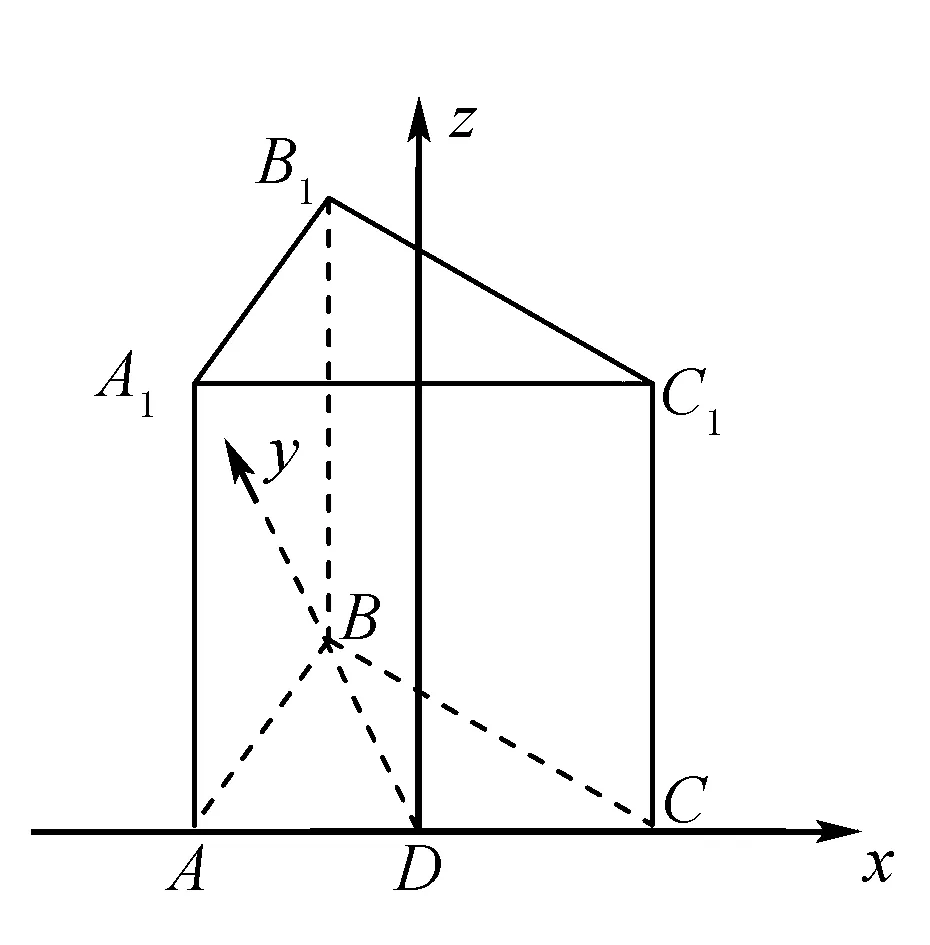
解 如图所示建立空间直角坐标系，点D为坐标原点，依题意可得A(-4,0,0)，B(0,3,0),C(4,0,0),B1(0,3,6).易得

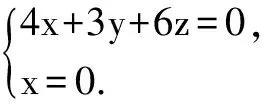
即n=(0,-2,1).令点B到面AB1C的距离为d,

则d=

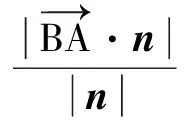
三、向量求线线位置关系

(1)恰当的构建空间直角坐标系；

(2)正确求得所对应点的坐标，空间向量的坐标表示及其数量积；

(3)代入空间向量的夹角公式，求得其余弦值；

(4)根据题意，转化为几何结论.

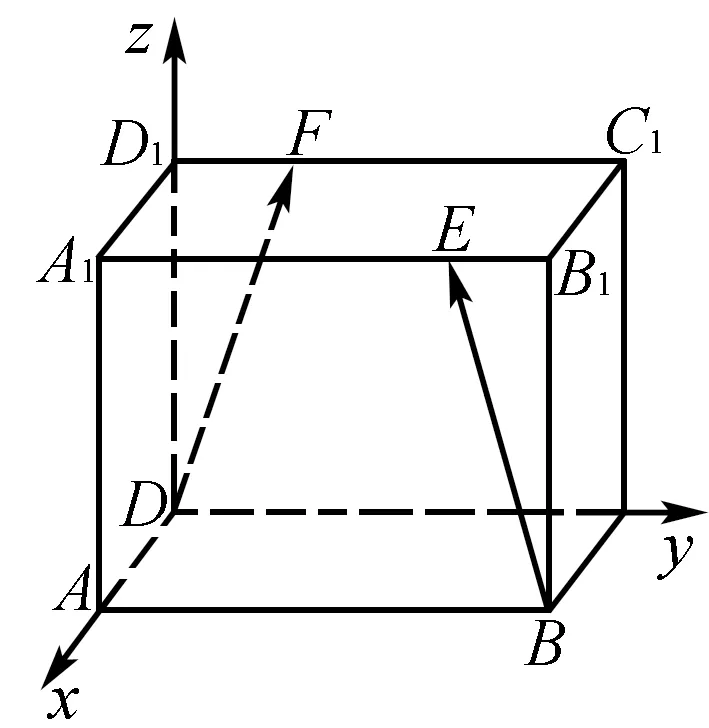
例3 在正方体ABCD-A1B1C1D1中，点E1、F1分别为A1B1，C1D1的一个四等分点，求DF1与BE1所成角的余弦值.

解 以点D为坐标原点建立空间直角坐标系如图所示.

设DD1=4,则D(0,0,0),F1(0,1,4),B(4,4,0),E1(4,3,4).

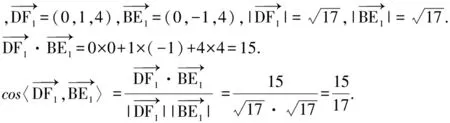
所以DF与BE所成角的余弦值为15/17.空间向量在立体几何中的应用十分广泛，其主要思想就是将立体图形放在合适的坐标系中，将图形量化，函数化.从而达到图形与函数结合，抽象问题具体化，系统化.

[1] 冯峰.分类例说空间向量在立体几何解题中的应用[J].高中数理化,2013.

[2] 杨建筑.例谈运用空间向量法解立体几何题[J].中学生数理化:高考版,2011.

2017-05-01

曾石明(1990-)，男，江西赣州人，大学本科，中学二级教师，主要从事高中数学教学研究.

G632

B

1008-0333(2017)19-0056-02