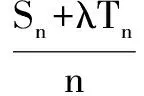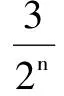谈数列中的数论问题
2017-09-03陈飞
陈 飞
(江苏省如皋市长江高级中学,江苏 南通 226500)
谈数列中的数论问题
陈 飞
(江苏省如皋市长江高级中学,江苏 南通 226500)
在高中数学《数列》中,经常出现满足一定条件下的数列项的存在问题,或求解涉及到整数n的不定方程,可以归纳为数论的基本问题.在近几年全国各省市的高考数学中,也时常出现上述问题.下面结合具体实例,谈谈对这类问题的处理方法.
高中数学;数列
一、利用合数的分解定理
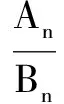
A.2 B.3 C.4 D.5
解 通过
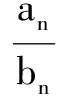

二、奇偶性分析
例2 已知{an}前n项之和为Sn,满足Sn=2an-3n(n∈N*).
(1)求证:{an+3}为等比数列,并求{an}通项公式;
(2)数列{an}中是否存在三项,使它们按原顺序可以构成等差数列?若存在,求出一组适合条件的项;若不存在,说明理由.
略解 (1)an=3(2n-1) (n∈N*).(2)假设存在{an}中三项ar、as、at(r ∴6(2s-1)=3(2r-1)+3(2t-1),∴2s+1=2r+2t①. ①中两边除以2r,∴2s+1-r=1+2t-r②. ∵r,s,t∈N*,且r ∴②中左边为偶数,右边为奇数. ∴假设不成立.即不存在三项,使它们成等差数列. 例3 已知{an}前n项和Sn满足Sn+1=kSn+2,又a1=2,a2=1.(1)求k值;(2)求Sn; (3)假设存在,m、n∈N*,满足条件, ∴2<(4-m)·2n<6,又m,n∈N*,(4-m)·2n为偶数,∴(4-m)·2n=4=2×2=1×4. ⟹(p-r)2=0⟹p=r矛盾.∴假设不成立.即原命题成立. (1)求{an}通项公式; (2)d∈{a1,a2,a3,…,an}∩{b1,b2,b3,…,bn},则称d为数列{an}与{bn}的公共项,将这些公共项按它们在原数列中顺序排成一个新数列{dn},求{dn}的通项公式. (1)令bn=an+1-an-1,求证:{bn}是等比数列; (2)求{an}通项公式; Sn+λTn=An2+Bn①. [1] 卓水鑫.高中数学解题中构造法的巧妙运用[J].新课程学习,2014(4):75—77. [责任编辑:杨惠民] 2017-05-01 陈飞(1984-),男,江苏如皋人,中学一级,大学本科,从事高中数学教学. G632 B 1008-0333(2017)19-0051-02三、利用在某一范围内整数的有限性


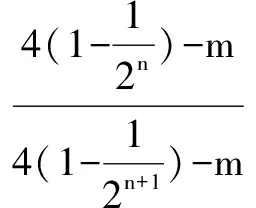
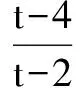

四、利用反证法证明某些问题
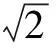
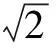
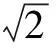

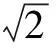
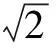
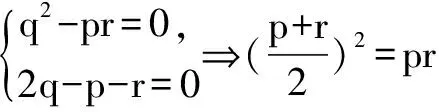
五、利用二项式展开定理


六、利用{an}是等差数列⟺an=An+B(A、B为常数)