例谈高中三角函数求值题的解题技巧

张新艳

(山东省济南市平阴县第一中学，山东 济南 250400)

例谈高中三角函数求值题的解题技巧

张新艳

(山东省济南市平阴县第一中学，山东 济南 250400)

三角函数是高中数学教学的重要组成部分，具有高度抽象性的特点，对学生的逻辑分析能力、归纳总结能力要求较高.而且三角函数也是高考的重要考点，题型多变.鉴于此，为了减少学生的学习难度，提高学生的解题速度，高中数学教师应当重视从多方面、多层次培养学生的三角函数解题技巧.本文主要针对常见的三角函数解题方法进行讨论.

三解函数；解题；技巧

一、角转化求值

在一些三角函数求值题目中，正余弦、正余切以及正余弦角度之间的求值虽然简单，但是形式多变对学生的思维能力要求较高.对于此类题型，学生应当懂得万变不离其宗这一道理，并灵活运用三角函数公式，进行快速化简.需要注意的是学生在进行化简时应当认真仔细，避免出现遗漏、丢失情况，以致于出现思路正确，而结果错误的现象.

例如这样一道题目：求sin20°cos70°+sin10°sin50°的值.显然，题目中给出的并非是常见特殊角.为此，在求解时可以根据积和化差公式sinαsinβ=-[cos(α+β)-cos(α-β)]/2，sinαcosβ=[sin(α+β)+sin(α-β)]/2 两个公式进行转化.将sin20°cos70°转化为sin20°sin20°；sin10°sin50°转化为-[cos(10°+50°)-cos(10°-50°)]/2，再进一步进行化简可得到：(1-cos60°)/2=1/4.从中能够看出，角的转化是相当灵活的，学生在应用时也要适当地灵活应用.这样才能快速解题，节省解题时间.

上述例题是正余弦之间的转换，而在实际的三角函数题目中还包含正余弦、正余切之间的转化.如这样一道题目：已知tanα=2，求(4sinα-2cosα)/(5cosα+3sinα)的值.显然，这道题目并没有给出具体角度，而只是给出了正切值，来求解一个复杂的正余弦三角函数值.对此，可以灵活应用tanα=sinα/cosα这一公式，将所求式子的分母、分子同除以cosα.经过化简可得到：(4tanα-2)/(5+3tanα)=10.从上述两道题目中能够对于这种需要相互转化的三角函数题目来说，学生应先完全把握住转化公式，并根据已知条件，求解式子罗列出相应的公式，并择其优者而用之，最终完成转化求值，缩短解题时间.

二、数形结合求值

有一些三角函数求值题目与图形息息相关.单纯依靠学生的想象力找寻解题思路比较困难.对此种题目，教师就可以引导学生学会如何结合图形，快速完成题目求解.而且在日常教学中，教师还可以采用多种多样的教学方法逐步培养学生的画图习惯，一旦遇到能够通过图形解决的题目便可以充分发挥出图形的优势.但是有一部分题目既可应用数形结合方法，也可应用化简求值方法，学生可以根据自身的学习水平适当选择.

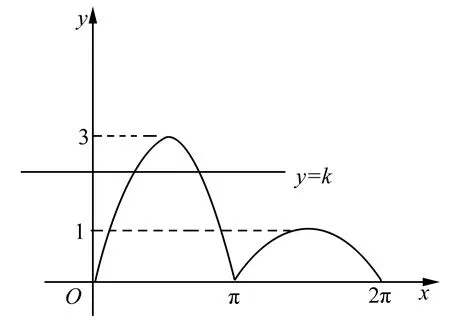
图1

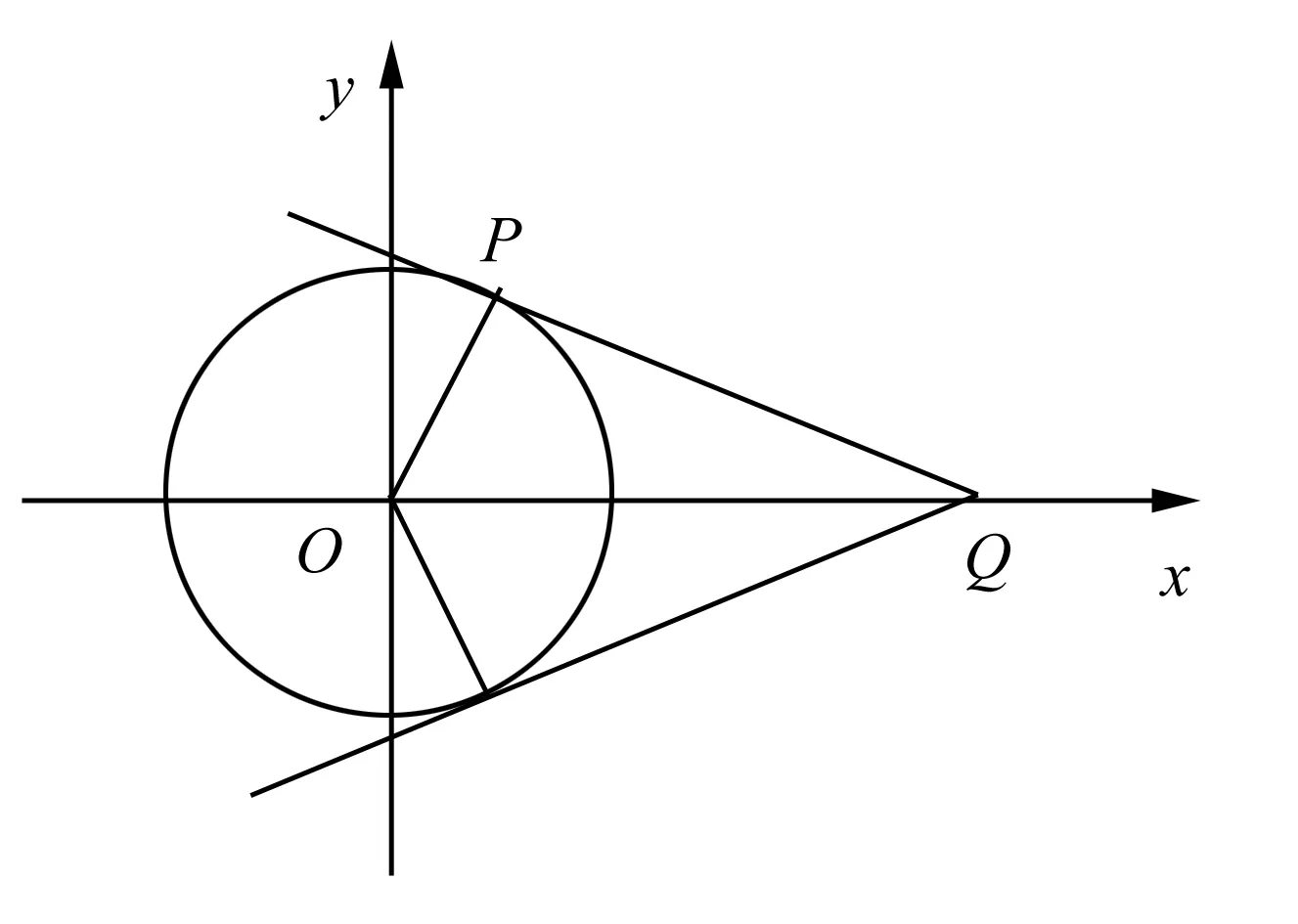
图2

三、升幂降幂

利用升幂降幂可以将高次幂的三角函数进一步进行化简.这种类型在三角函数求值题目中也比较常见.通常在解决这种问题时需要结合公式，如2cos2α-1=1-2sin2α=cos2α-sin2α=cos2α等公式.也就是说学生不仅要能够熟背这些公式，还能够结合题目加以应用.这样才能快速解决三角函数求值问题.当然，学生在化简的过程中，要尽可能地保证准确率，有时很可能会因为一丁点的错误得到错误结果，浪费解题时间.

例如这样一道题目：化简(1-cos4α-sin4α)/(1-cos6α-sin6α).解决这道题目最简单的思路便是通过将题目转化成为形式更加简单的题目，也就是说要尽可能地降低题目中的高次幂，以方便求解.但是明显题目中的幂数并不统一，若要进行化简就要选择升幂或者降幂.根据公式sin2α+cos2α=1，可将题目中的1进行适当的转化.如1-cos4α-sin4α可转化成为与之幂数相对等的(sin2α+cos2α)2-cos4α-sin4α.而在1-cos6α-sin6α中，再次提高sin2α+cos2α的幂数，简单的说是将原式子转化为(sin2α+cos2α)3-cos6α-sin6α.这样便能够整体将式子进行转化.而后经过加减运算，便能够得到最终的化简结果：原式子=2cos2αsin2α/3cos2αsin2α(sin2α+cos2α)=2/3.从中能够看出，升幂降幂选择的关键在于根据题目中原有的幂数，并灵活应用1这一关键数字.在三角函数中，sin2α+cos2α=1这一公式在多种求值题目中均可应用.总的来说，高中数学教师应重点培养学生的灵活性思维，能够根据题目进行适当的转化，从而提高三角函数解题速度.

三角函数既是高中数学的重点、难点，也是数学抽象性的集中体现.为此，教师在教学时应重视采用灵活的教学方法，加深学生对三角函数公式的记忆，并结合各种练习题目，提高学生的实践能力，最终提高学生的解题效率.总之，是在新课改逐渐深入的背景下，数学教师在教学时应当摒弃传统的灌输式教学模式，避免学生对数学产生厌恶情绪.尤其是三角函数求值题目较难，需要学生花费较长的时间钻研、熟知、掌握，教师应当充分发挥自身的引导作用，帮助学生真正掌握三角函数求值题的解题技巧.

[1]黄婵.三角函数求值的分类辨析[J].教育教学论坛,2015(10)：174-176.

[2]彭万雷.例析三角函数求值题的解题技巧[J].华夏教师,2016(12):37.

[责任编辑：杨惠民]

2017-05-01

张新艳(1980.01-)，女，山东济南人，平阴一中，中学二级，本科，高中数学教学.

G632

B

1008-0333(2017)19-0015-02