浅谈应用向量解决高中几何习题的方法

邓卫和

(江苏省阜宁中学,江苏 盐城 224000)

浅谈应用向量解决高中几何习题的方法

邓卫和

(江苏省阜宁中学,江苏 盐城 224000)

向量，是一种具有几何、数量、方向性质的数学概念，它经常应用于坐标图形上，进行空间、数量及方向的计算.本文对此进行了分析研究.

向量；解决；高中；几何；习题

谈到向量的概念，很多同学对向量概念的理解局限为数量和方向这两个要素上.实际上，向量具有数量、几何、坐标三重性质.如果同学们能够灵活的应用这三重性质，就能应用向量公式高效的解出数学习题.

一、应用向量将几何变为方程

很多同学在解方程的时候，没有想过向量就是一个方程.即使现在谈到向量就是一种特殊的方程，可能部分同学们还是难以理解.向量，不是表示方向和大小的吗？它怎么会是一种方程呢？同学们要看到，在坐标图形上，一元一次方程，代表着向某一个方向无限延伸的直线；向量，在坐标图形上代表着向某一个方向无限延伸的直线.那么在坐标图上，方程不是和向量有着共通性吗？如果同学们在解方程的时候，应用向量的计算公式，可以不可以简化方程的计算呢？现用习题1为例.

习题1：已知在△ABC中，三个顶点分别为A(0，-4)、B(4，0)、C(-6，2)，而点E、F、D分别为AB、AC、BC的中点，求直线FD、EF、DE的方程.

同学们要了解，在坐标图形上，向量具有方程的性质，同学们在解方程的时候，如果遇到计算方程的问题，可以把方程问题变成向量问题，应用向量平移、向量座标计算的方法求取方程.

二、应用向量确定立体几何关系

同学们在做几何习题的时候，有时需要证明图形和图形之间的几何关系.一般地，同学们会用几何图形的性质来证明.然而有时同学们在证明的时候会遇到几何求证的条件不全，同学们难以应用几何图形的性质.向量既具有空间图形中指示方向的特性，又有空间图形中指示数量的特性，同学们在证明几何图形时，可以把几何图形变成向量，就用向量数的特征来转换空间图形的数与量.现用习题2为例.

习题2 在正方体ABCD-A1B1C1D1中E是棱DD1的中点.请问在棱C1D1上是否存在一点F，使B1F∥平面A1BE？请证明.

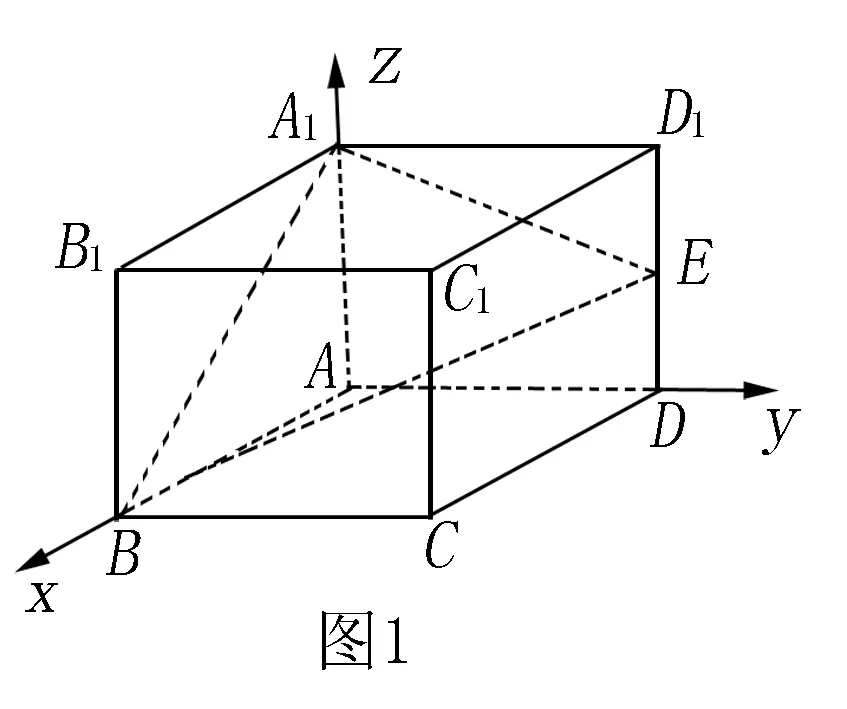
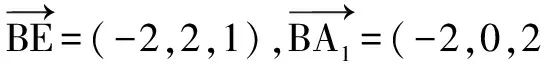
同学们看到，习题2给出的证明条件非常抽象，如果同学们要用几何性质来证明，过程会非常繁琐.现在，将几何问题变为解析几何问题.应用特殊取值法，取出空间几何中的数值，应用向量计算坐标.同学们再将计算出的坐标还原成几何证明问题，就能轻易地证明出几何问题.

同学们要意识到，同学们在证明几何问题的时候，如果可以应用特殊取值法来证明几何问题，就可以将几何问题变为坐标图形，应用向量的方式计算出几何图形的座标位置确定几何图形，再应用几何性质来证明.

三、应用向量求取几何夹角

同学们在解决几何问题的时候，有时需要处理几何图形的边、角问题，有时同学们应用几何性质来解析几何，解题的过程会比较繁琐.如果同学们把向量图形的方向特性，与数的特性结合起来，便能用数、形、方向三重特性来呈现几何图形，同学们可以应用这种方法，灵活的转换几何图形的边长、图形、角的性质，获得需要的几何图形数值.现用习题3为例.

习题3 已知正方体的棱长为1，求它的对角线与它任何一个面的对角线的夹角.

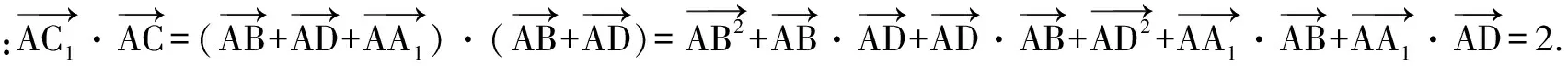
同学们可以看到，这一题就是把空间几何图形变为坐标图形，又将解析几何图形变为向量计算，应用向量公式计算出几何图形的边长，求取几何图形角的案例.习题3里，已经给出了正方体的棱长，同学们可以直接应用几何图形性质来解析这道题.然而应用解习题2的思路来看，应用解析几何的方式来解这道习题，会让解题的过程变得简单.

[1]张凤莲.高中数学中的向量研究[D]. 华中师范大学,2007.

[2]彭勇.关于向量及其教学研究[D]. 华中师范大学,2006.

[责任编辑：杨惠民]

2017-05-01

邓卫和(1970.10-)，男，江苏阜宁人，中学一级教师，大学本科，从事高中数学研究.

G632

B

1008-0333(2017)19-0042-02