构造等差数列解无理方程组

张邹黄

(江苏省如皋市长江高级中学,江苏 南通 226500)

构造等差数列解无理方程组

张邹黄

(江苏省如皋市长江高级中学,江苏 南通 226500)

本文主要讨论如何构造等差数列解读某些非数列的无理方程组问题，供师生教学参考.

高中数学；等差数列；方程组

①

②

思路分析 本题若用平方法，对①式进行两次平方去掉根号求解，不仅运算复杂，而且也很困难.然而注意到①式的特征“两数之和是第三数”.应用构造等差数列的方法求解，化繁为简、变难为易.

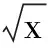
③

④

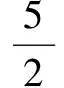
⑤

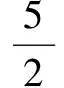
⑥

将⑤和⑥同时代入②中化简整理，得

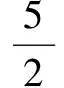
⑦

再将⑦代入⑤和⑥中，即可得到

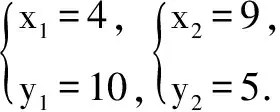
点评 本题解法的巧妙之处在于通过构造等差数列，避免了传统解法中脱根号的繁琐运算.

①

②

思路分析 本题可根据等式①的结构特征，通过构造等差数列求解，这样可使运算简化.

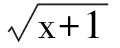
③

④

所以③2、④2,得

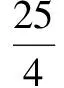
⑤

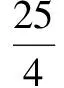
⑥

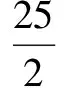
⑦

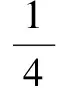
例3 解方程组

①

②

③

④

由③2、④2得

⑤

⑥

故⑤+⑥,得

⑦

而由②将8拆成3和5可得

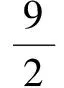
⑧

再将⑧代入⑤、⑥中，可得到

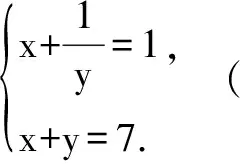
经检验上述四组解都是原方程组的解.

综上所述可知：上述三例均是从方程组中第①式入手，通过构造等差数列，设公差为d，将方程组中第②式变形为关于d的二次方程，求出d的数值后，进而求得方程组的解.

[1]李传军.证明数列不等式容易被“遗忘”的几种策略[J].才智,2009(12).

[2]翟佳妮.高中数学竞赛和高考中数列不等式的问题研究[D].西北大学,2015.

[责任编辑：杨惠民]

2017-05-01

张邹黄(1983-),男,江苏如皋人,中学一级，大学本科，从事高中数学教学.

G632

B

1008-0333(2017)19-0037-02