基于本质找视角 一题多解得方法

何建东

(浙江省绍兴市越州中学,浙江 绍兴 312075)

基于本质找视角 一题多解得方法

何建东

(浙江省绍兴市越州中学,浙江 绍兴 312075)

问题是数学的心脏，数学问题不仅包含了重要的数学知识与思想，还常蕴藏着数学最核心的素养.因此，寻求数学问题的解决办法时，需要我们“基于本质”去找视角，方能得“一题多解”的方法.本文就如何基于数学本质，多视角解答试题进行剖析.

数学本质；一题多解；高考

命题说明 这个问题以含双参数a,b的二次函数模型为基础，结合函数图象与零点存在情况，设置了求解两个参数a,b的代数式取值范围.应该说问题涉及的数学知识与思想是中学阶段最重要的内容之一，问题类型既有常见的感觉，亦有常新的味道，相信广大师生们一定会仁智互见，各有办法.但，如果能从数学本质与核心素养出发，对问题进行多视角的剖析，可为数学教学带去更大的价值.

追本溯源 函数与方程是中学数学两块重要内容，其中蕴含着方程思想、函数思想和数形结合思想和化归思想等.基于此，我们可以从方程等式的角度寻找变量与参数之间的内在联系；也可以从函数图象的结构特征寻找条件与结论的内在属性；还可以通过“规划型”问题的数形结合解法求得结果.

视角一：函数零点视角

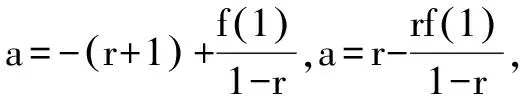
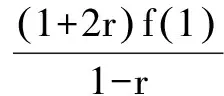
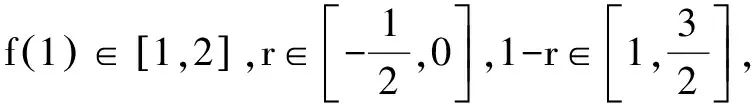
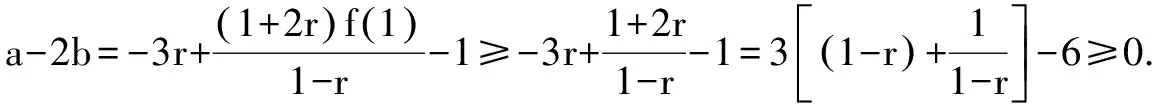
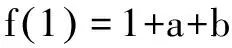
视角二：方程实根视角

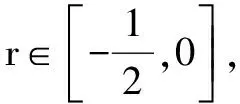
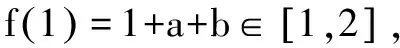
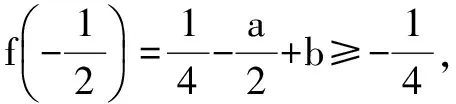
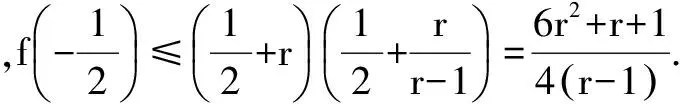
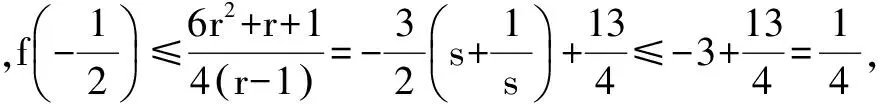
综上所求，有0≤a-2b≤1.

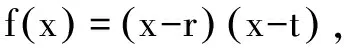
视角三：规划问题视角

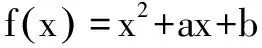
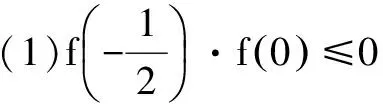
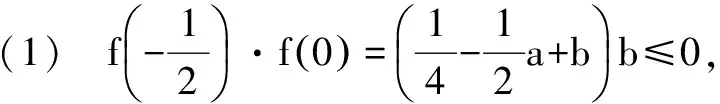
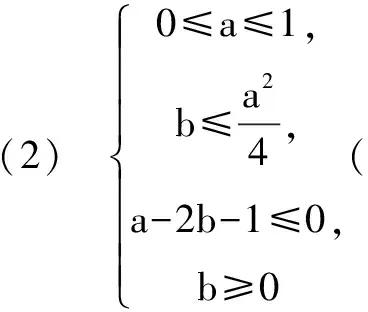
又因为条件：0≤a+b≤1(※※※)，

可以平面直角坐标系aOb中作图进行求解.

因此，a-2b的取值范围为0≤a-2b≤1.

[1]浙江省教育厅.浙江省新高考学科教学指导意见[Z]，2014．

[责任编辑：杨惠民]

2017年3月17日

何建东(1975.11-)，男，浙江诸暨人，高级教师，数学教育硕士，从事适应浙江新课改考改的高中数学有效教学.

G632

B

1008-0333(2017)19-0027-02