Theory of Quantum Dissipation in a Class of Non-Gaussian Environments

Rui-xue Xu,Yang Liu,Hou-dao Zhang,YiJing Yan

Hefei National Laboratory for Physical Sciences at the Microscale and Department of Chemical Physics and Synergetic Innovation Center of Quantum Information and Quantum Physics andiChEM,University of Science and Technology of China,Hefei 230026,China

(Dated:Received on June 17,2017;Accepted on June 27,2017)

Theory of Quantum Dissipation in a Class of Non-Gaussian Environments

Rui-xue Xu,Yang Liu,Hou-dao Zhang,YiJing Yan∗

Hefei National Laboratory for Physical Sciences at the Microscale and Department of Chemical Physics and Synergetic Innovation Center of Quantum Information and Quantum Physics andiChEM,University of Science and Technology of China,Hefei 230026,China

(Dated:Received on June 17,2017;Accepted on June 27,2017)

In this work we construct a novel dissipaton-equation-of-motion(DEOM)theory in quadratic bath coupling environment,based on an extended algebraic statistical quasi-particle approach.To validate the new ingredient of the underlying dissipaton algebra,we derive an extended Zusman equation via a totally different approach.We prove that the new theory, if it starts with the identical setup,constitutes the dynamical resolutions to the extended Zusman equation.Thus,we verify the generalized(non-Gaussian)Wick’s theorem with dissipatons-pair added.This new algebraic ingredient enables the dissipaton approach being naturally extended to nonlinear coupling environments.Moreover,it is noticed that, unlike the linear bath coupling case,the in fluence of a non-Gaussian environment cannot be completely characterized with the linear response theory.The new theory has to take this fact into account.The developed DEOM theory manifests the dynamical interplay between dissipatons and nonlinear bath coupling descriptors that will be speci fied.Numerical demonstrations will be given with the optical line shapes in quadratic coupling environment.

Non-Gaussian environment,Quantum dissipation,Dissipaton theory

I.INTRODUCTION

Quantum dissipation plays crucial roles in many fields of modern science.Exact theories include the Feynman-Vernon in fluence functional path integral approach [1],and its differential equivalence,the hierarchicalequations-of-motion(HEOM)formalism[2–6].However,almost all existing quantum dissipation theories exploit the Gaussian-Wick’s thermodynamical statistics[7–9],which is strictly valid only for linear bath couplings.Intrinsically,a linear bath coupling implies a weak backaction of system on environment. The lowest non-Gaussian environment in fluence requires a quadratic bath coupling.

In this work,we extend the dissipaton equation of motion(DEOM)theory[10,11]to treat the linearplus-quadratic bath coupling environment.This theory goes with a statistical quasi-particle(“dissipaton”) description for the hybrid environment that can be either bosonic or fermionic or excitonic.Dynamical variables in DEOM are the dissipaton density operators (DDOs),for both the reduced system and the hybrid bath dynamics[10,11].The latter could also be measured experimentally,via such as the Fano interference[12–16],vibronic spectroscopy with non-Condon polarized environment[17],and transport current noise spectrum[18].

Dissipaton algebra plays essential roles[10,11].It consists of the generalized(non-Gaussian)Wick’s theorem and the generalized diffusion equation.This noval algebra leads to the rules on how the DDOs evolves in time,and further on their relations to experimental measurable quantities that involve explicitly the hybrid bath dynamics[14–18].From the algebraic construction point of view,the new DEOM theory in quest amounts to the establishment of the generalized Wick’s theorem with dissipatons-pairs added.This will be the new ingredient of the dissipaton algebra for treating the quadratic bath coupling in study.

Another important issue is concerned with the characterization of nonlinear coupling bath.On top of the interacting bath correlation function description[7–9], additional information would be needed.This is a general concern in any non-Gaussian environment theories. To address this issue,we propose a polarization model to determine both the linear and nonlinear bath coupling strengths.This model resolves this issue,with a single additional parameter,on top of the conventional linear response theory.

In this work,we construct the DEOM formalism,via the dissipaton algebra,including the aforementioned new ingredient for treating quadratic bath coupling. We validate this new ingredient,the generalized Wick’s theorem with dissipatons-pairs added.To do that we derive an extended Zusman equation via a totally different approach.We prove that the DEOM formalism, if it started with the same setup,constitutes the dynamical resolutions to the extended Zusman equation.Therefore,as the algebraic construction is concerned, we would have also con firmed the DEOM formulations. The linear and quadratic bath coupling strength parameters,will be discussed on the basis of the nonlinear polarization model.Numerical DEOM demonstrations are then carried out on the optical line shapes in the nonlinear coupling environment.

II.DISSIPATON DYNAMICS THEORY

A.Statistical quasi-particle description

Let us start with the total composite Hamiltonian,

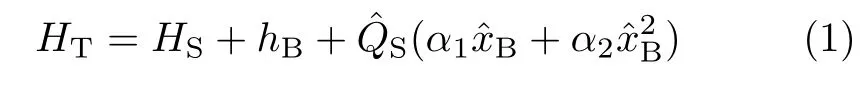
The system Hamiltonian HSand dissipative operator ˆQSare arbitrary.The latter is set to be dimensionless.The bath Hamiltonian and the hybridization bath operator(solvation mode)are given,respectively,

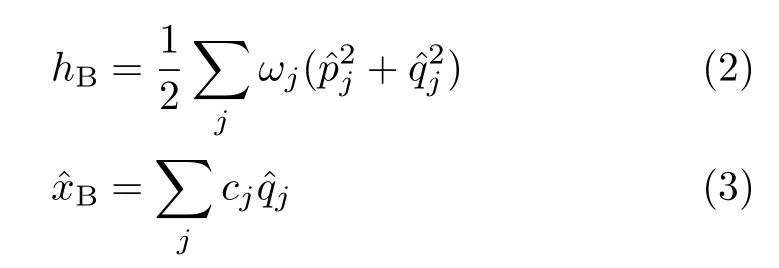
Throughout this work we set ħ=1 and β=1/(kBT),with kBand T being the Boltzmann constant and temperature.Letbe the bare bath ensemble average.De fineSet hereafter t≥0 for the time variable.We have[7,9]

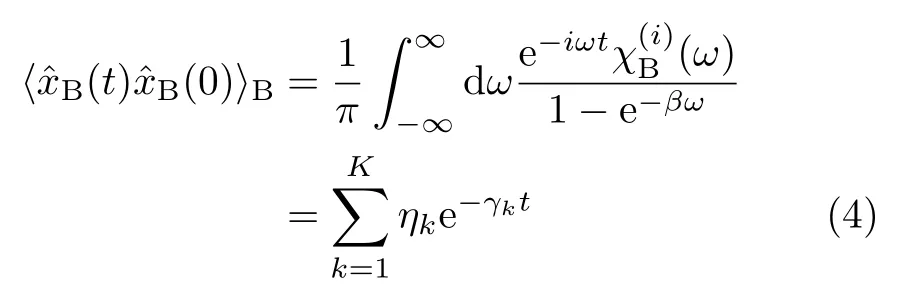
The first expression in Eq.(3)is the fluctuationdissipation theorem[7,9],withbeing the imaginary part of

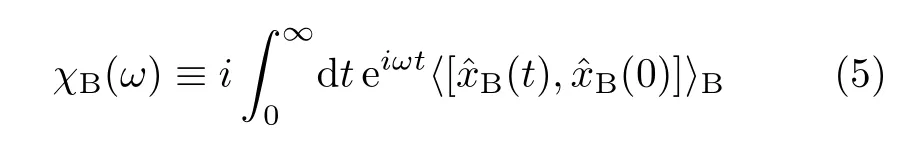
The second expression of Eq.(4)presents an exponential series expansion of the linear bath correlation function.Set hereafterˆxBto be dimensionless,so that the bath coupling parameters,α1and α2in Eq.(1),are of frequency unit.It is well known that,for a complete characterization of the nonlinear environment in fluence (α2≠0),additional information,on top of Eq.(4),is needed.We will address this issue latter.

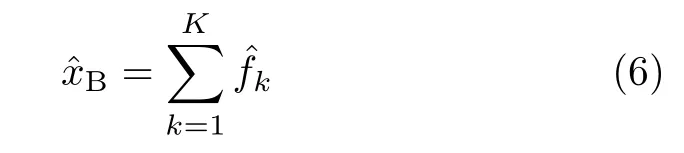
with

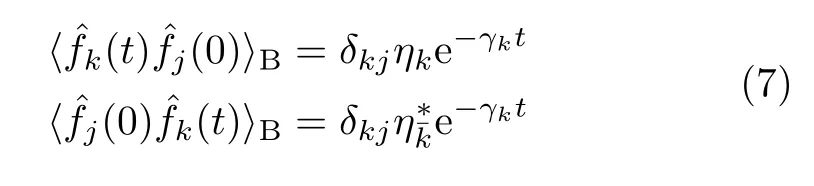
As de fined in Eq.(7),dissipatonsare statistically independent quasi-particles.Each of them is a macroscopic linear combination of bath degrees of freedoms. Individualis characterized by a single damping parameter,γk,that can be complex,and a joint-pair of interacting strength parameters,

B.Dissipaton algebra and DEOM formalism

Dynamical variables in DEOM are dissipaton density operators(DDOs)[10,11]:

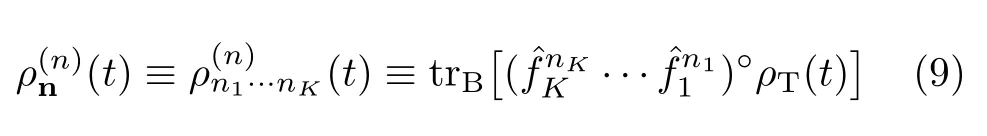
The dissipatons product inside(···)◦is irreducible,such that(c-number)◦=0.Bosonic dissipatons satisfy the symmetric permutation,(ˆfkˆfj)◦=(ˆfjˆfk)◦.Physically, each DDO of Eq.(9)stands for a given con figuration of the total n=n1+···+nkdissipatons.Denote for the use below the associated DDO’s index,n±k,which differs from n≡n1···nKat the speci fied nkby±1. Similarly,n±±kjdiffers from n at the speci fied nkand njthat are replaced by nk±1 and nj±1,respectively.

The DEOM formalism can be easily constructed via the algebraic dissipaton approach[10,11].The construction starts with applying the Liouville-von Neuman equation,˙ρT(t)=−i[HS+hB+HSB,ρT(t)],for the total density operator in Eq.(9).The bath hB-action and the system-bath coupling HSB-action are then readily evaluated with the generalized diffusion equation and the generalized Wick’s theorem,respectively.

The generalized diffusion equation arises from the single-damping parameter characteristic,as shown in Eq.(7),for both its forward and backward correlation functions.This feature leads to[10,11]

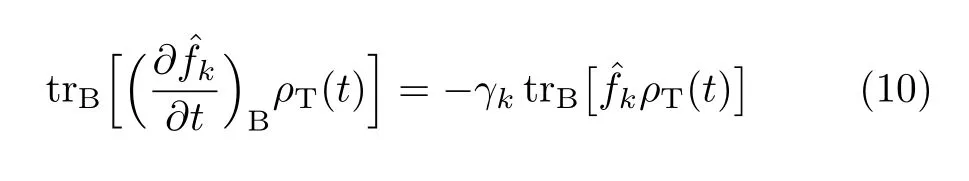
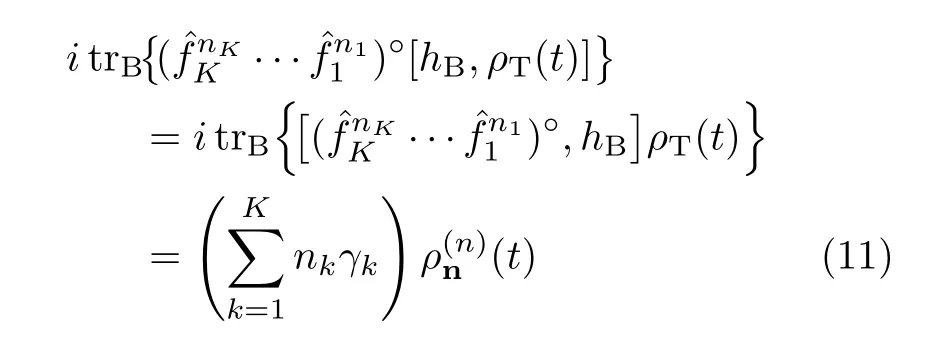
This is the bath hB-action contribution to the DDOs dynamics.The generalized diffusion Eq.(10)or Eq.(11), with an arbitrary total composite ρT(t),has been validated previously[10,11].

The generalized Wick’s theorem(GWT)deals with the system-bath coupling HSB-action[10,11].In this work this theorem has two ingredients,GWT-1 and GWT-2,in relation to the linear and quadratic bath couplings,respectively.The GWT-1 reads[10,11]

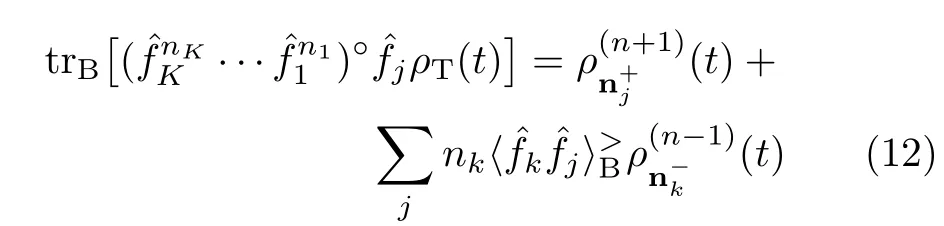
The GWT-2 is concerned with the quadratic bath couplings,where a pair of dissipatonsparticipate in simultaneously without time-ordering.This new ingredient of dissipaton algebra would read

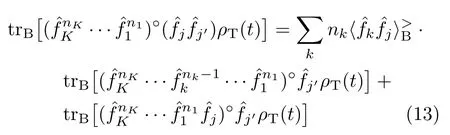
with the last term being evaluated as

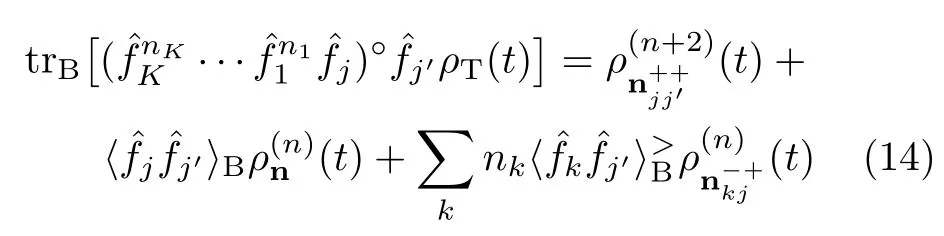
Together with the first term in Eq.(13)being evaluated via GWT-1,we obtain

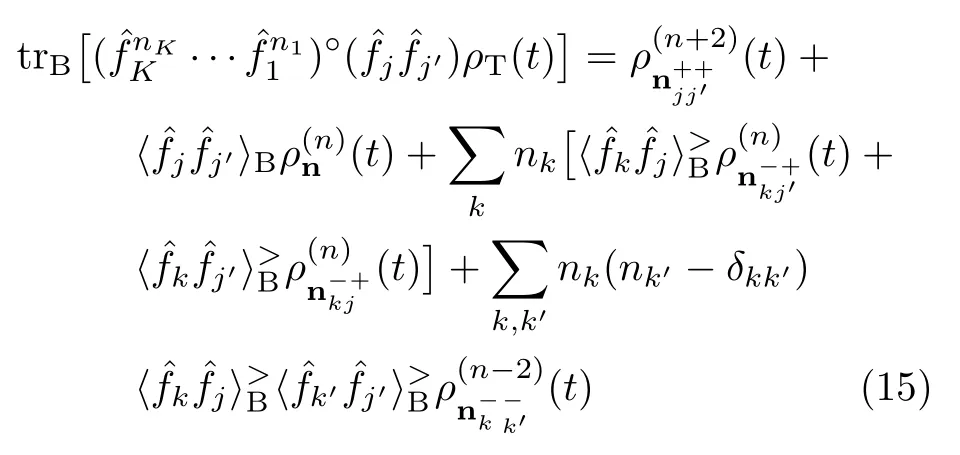
The DEOM formalism in the presence of both linear and quadratic bath couplings can now be readily constructed via the above dissipaton algebra.The final results read

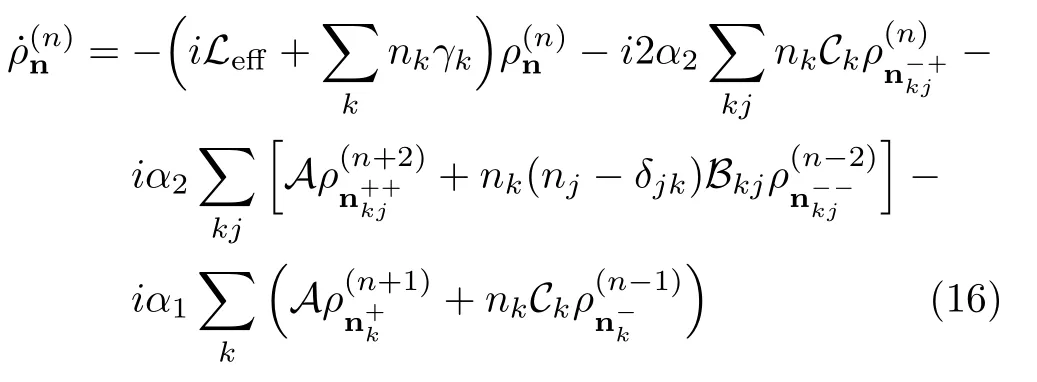
Here,

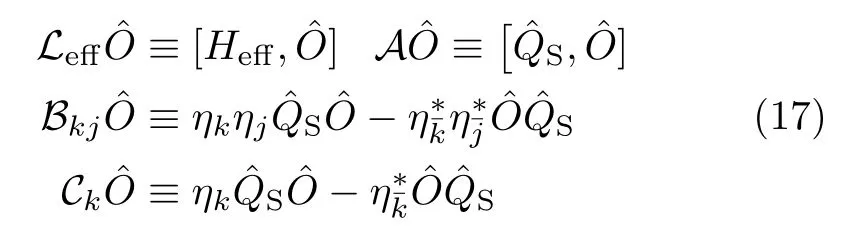
with

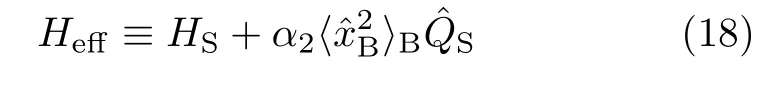
Evidently,the dissipatons de fined in Eqs.(4)−(7)are strictly based on the linear bath coupling part that satis fies Gaussian-Wick’s statistics[7–9].The quadratic non-Gaussian bath in fluences are treated via the GWT-2,Eq.(15).This is the virtue of the DEOM theory that includes the powerful dissipaton algebra[10,11].In general,Eqs.(10)−(15)are all non-Gaussian operators in the system subspace.

III.VALIDATION ON DISSIPATON ALGEBRA WITH EXTENDED ZUSMAN EQUATION

This section is devoted to validating the GWT-2, Eqs.(13)and(14),the new ingredient of the dissipaton algebra presented above.It together with the wellestablished Eqs.(10)and(12)lead immediately and unambiguously to the extended DEOM(Eq.(16)).Therefore,from the algebraic construction point of view,the required validation can be made with the dissipaton basis set of size K=1.This amounts to the formal setting Eq.(4)with

The dissipaton index n can be omitted;i.e.,ρ(n)n(t)= ρ(n)(t)≡ˆρn(t),for the basis set size K=1 case,in which the DEOM(Eq.(16))readsThe involving superoperators A,B and C,are the same as those in Eq.(17),but without dissipaton indexes.

In the following,on the basis of Eq.(19)which will be called the Zusman setup,we construct the extended Zusman equation via a totally different approach.By showing that the extended Zusman equation is identical to Eq.(20),we validate the dissipaton algebra and thus the extended DEOM theory,Eq.(16).The proof here is rigourous,due to the nature of the algebraic construction,despite of the fact that the Zusman setup,Eq.(19), itself could even be a bad approximation.

It is well known that the Zusman setup,Eq.(19),is equivalent to the combination of the high-temperature (HT)and the Smoluchowski limits.The HT limit is characterized with

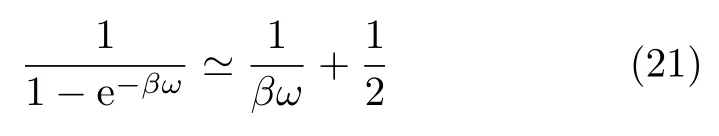
In this case,the solvation mode is a classical Brownian motion in the secondary bath environment.The latter exerts a stochastic forceand friction constant ζ on the solvation mode.The corresponding Langevin equation reads

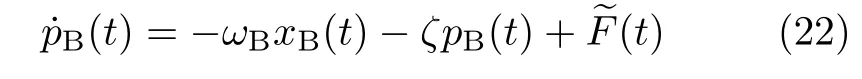
with

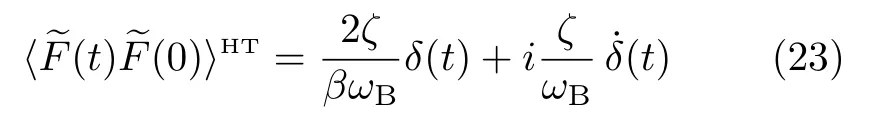
This is the high-temperature fluctuation-dissipation theorem. The resultant Caldeira-Leggett’s equation reads[19–21]

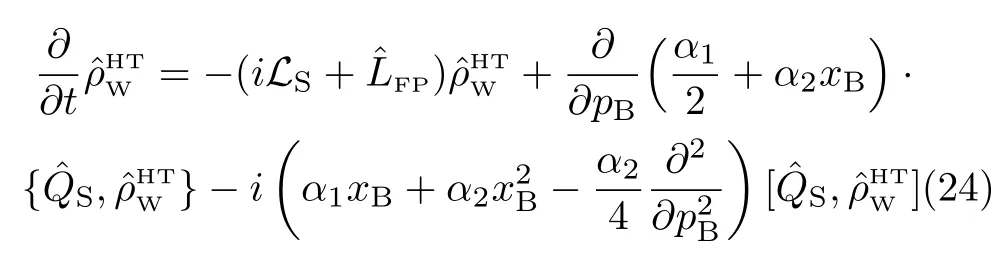
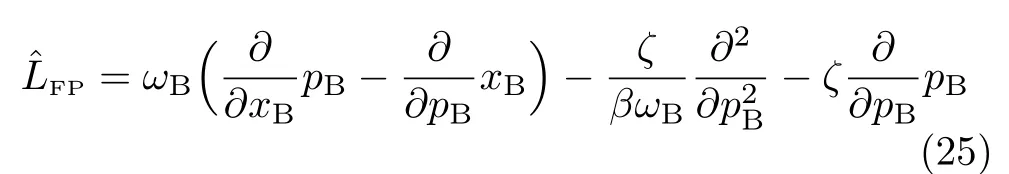
To complete the Zusman setup,Eq.(19),consider further the Smoluchowski(or strongly-overdamped)limit; i.e.,ζ≫ωB,whereas ω2B/ζ=γ remains finite to be the exponent in Eq.(19).Moreover,it is easy to show that〈x2B〉B=〈p2B〉B→ (βωB)−1,in the high-temperature limit.The identities here will be used in eliminating the appearance of βωBin the formulations below.The pre-exponential coefficient in Eq.(19)reads then

In the strongly-overdamped limit, the momentum pBwould no longerbe a correlated dynamical∫variable. Theequation ofmotion forwhich is closed now, can be obtained via the standard Fokker-Planck-Smoluchowski algorithm[22].

Another equivalent but much simpler approach is the so-called diffusion mapping method[23];i.e.,mapping each individual pB-space variable to its limiting diffusive xB-space correspondence.This method makes a simple use of the Langevin equation Eq.(22),which in the strongly-overdamped limit reduces to

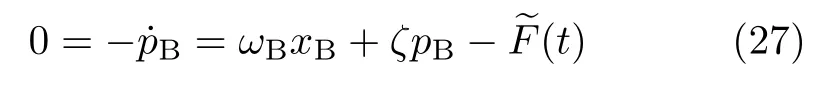
Consider further the following two thermodynamic relations,

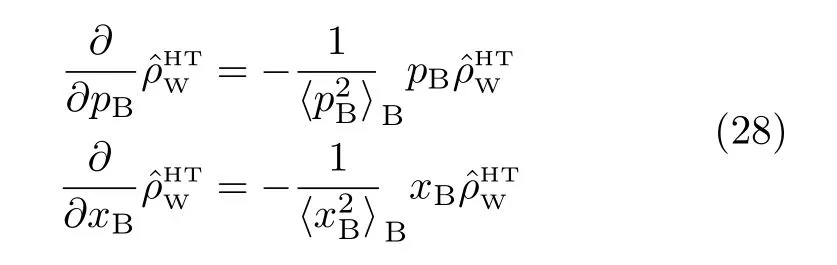
Together with pB/xB≃−ωB/ζ,as implied in Eq.(27), and〈x2B〉B=〈p2B〉Bin study here,we would have then

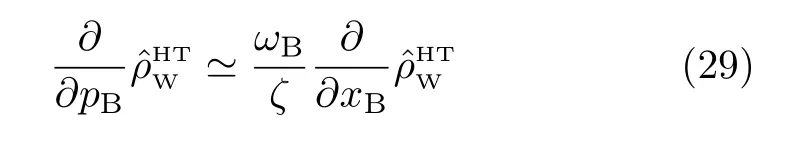
The above results of the Zusman setup lead to the following rules of diffusion mapping[23],

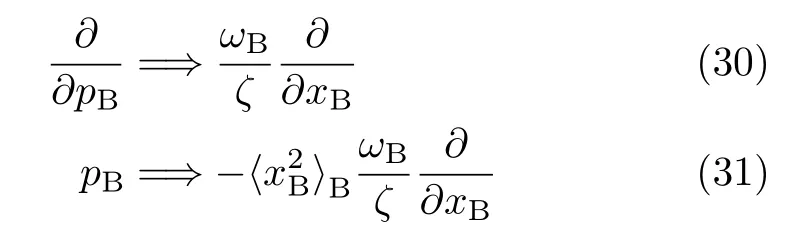
The Smoluchowski limit to the Calderia-Leggett’s master equation is now readily obtained by replacing all those pB-dependent operators in Eq.(24)and Eq.(25). In particular,the Fokker-Planck operator becomes the Smoluchowski or diffusion operator,

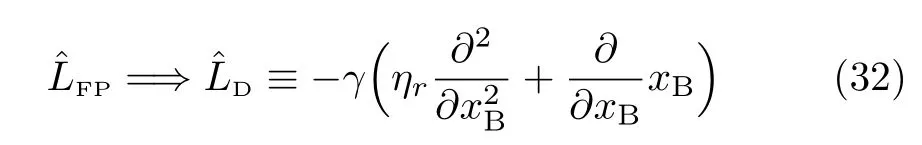
While ηr=〈x2B〉Bwas de fined in Eq.(26),γ=ω2B/ζ assumes the diffusion constant here.The Smoluchowski limit of Eq.(24)has an extended Zusman equation form,

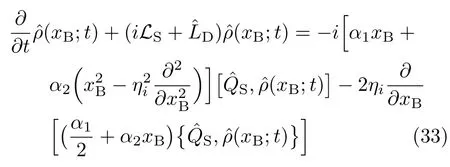
ThisrecoverstheconventionalZusman equation [24−26],in the absence of the quadratic bath coupling (α2=0).

We have also derived Eq.(33)via the standard Fokker-Planck-Smoluchowski approach[22];however, the derivations are too mathematical and tedious,see Appendix for details.The present universal diffusion mapping approach with Eq.(30)and Eq.(31)is much simpler and physically more appealing.

It is easy to verify that the DEOM formalism, Eq.(20),is just the dynamical resolution to the extended Zusman Eq.(33).More precisely,

or

where Hn(x)is the nth-order Hermite polynomial,and

We have thus validated the dissipaton algebra, Eqs.(10)−(15). This is the purpose of the above comparisons between the dissipaton approach and the present system-and-solvation composite description. The dissipaton algebra,including the new ingredient, Eq.(13)and Eq.(14),the generalized Wick’s theorem with dissipatons-pairs added,is also by de facto established.Therefore,the extended DEOM Eq.(16)for general cases is also validated,due to its algebraic construction nature.

IV.INTERPLAY BETWEEN DISSIPATONS AND ENVIRONMENT PARAMETERS

Turn to the issue on the bath coupling parameters, α1and α2.It is crucial to have a physical support on the nonlinear coupling bath descriptors.This issue is directly related to the extended DEOM theory,which should describe the dynamical interplay between dissipatons and nonlinear bath couplings.Erroneous descriptors of α1and α2would result in unphysical DEOM dynamics.

In the following,we propose a polarization model to determine both α1and α2.For clarity,we consider a chromophore system,with its ground|g〉and an excited |e〉states being engaged in optical excitations.The total system-and-bath composite Hamiltonian in the presence of external classical laser field E(t)assumes

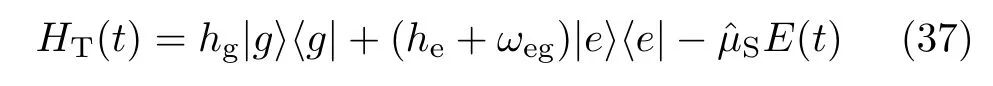
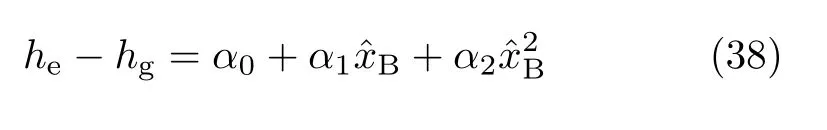
Here,hgand hedenote the bath Hamiltonians associating with the ground and excited system states,respectively.Eq.(37)assumes the form of Eq.(1);i.e.,

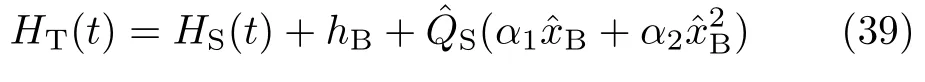
with the system Hamiltonian and dissipative mode,

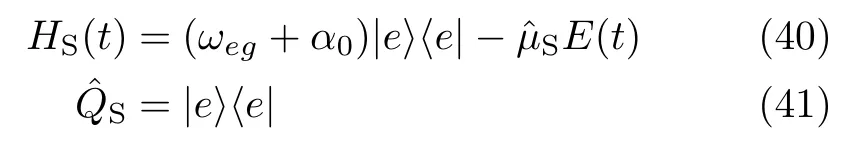
In Eq.(39)the bath Hamiltonian goes with hB=hg.

The polarization model assumes

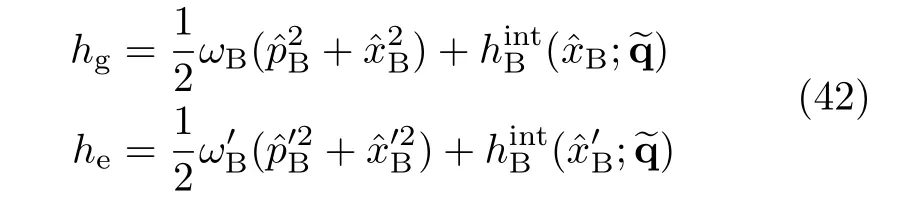
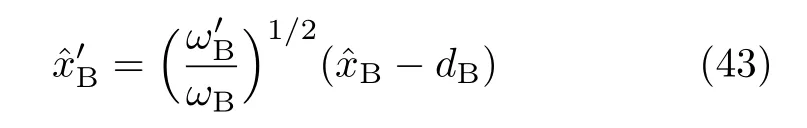
and

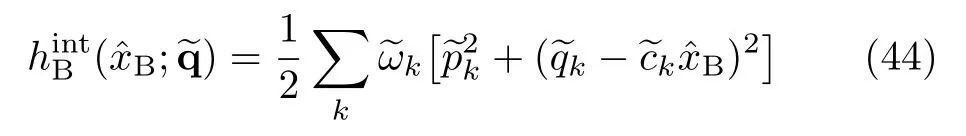
The physical picture of this model is as follows.The system is initially in the ground|g〉state,withˆxBdescribing its first solvation shell of frequency ωB.Upon excitation,the system in the excited|e〉state experiences different solvation environment.The reorganized first-shell solvation is described withIt has different frequency,and is also linearly shifted by dB, with respective to the ground-state solvation shell.The secondary environmentremains unchanged,as described by the samefor its interacting with eithersolvation mode.Apparently,the quadractic bath coupling vanishes when

The coupling strength of secondary bath with the solvation mode is given by

The renormalized frequencies forwould be

respectively.

To proceed, we consider first the linear–displacement–mapping (LDM)ansatz. Leth(1)ebe the special case of heat ω′B=ωB.The LDM ansatz assumes h(1)e−hg,due to a linear displacement dB,be the result within linear response theory.That is[9]

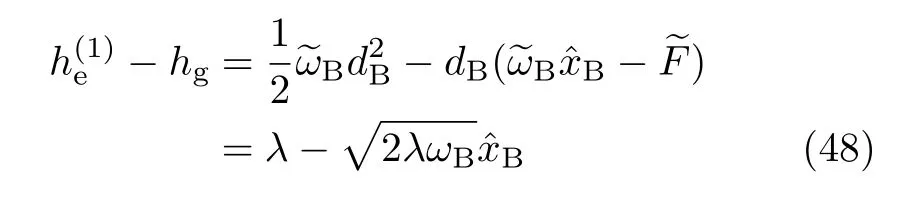
Here,

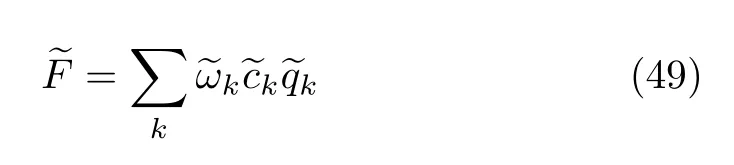
Consequently,

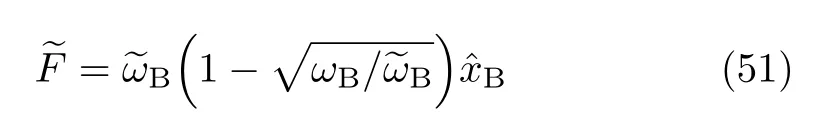
This relates the secondary bath,of Eq.(49),to the solvation coordinate

Substituting Eqs.(42)−(51)for Eq.(38),followed by some elementary algebra,we obtain

where

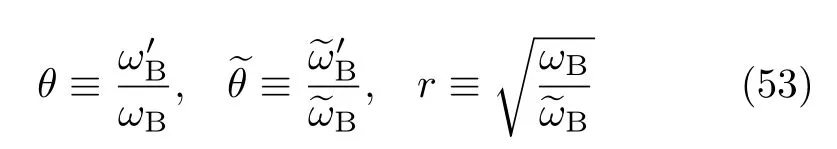
Moreover,the bath coupling α-parameters of Eq.(52) should go along with the underlying interplay with the dissipatons de fined in Eqs.(4)−(7).Given the temperature,dissipatons are determined byOn the other hand,the α-parameters in Eq.(52)are functions ofand λ.While the latter two are free variables,are dictated by the samethat determines the dissipatons.For the secondary bath coupling strength parameter(Eq.(45)),we have[9]

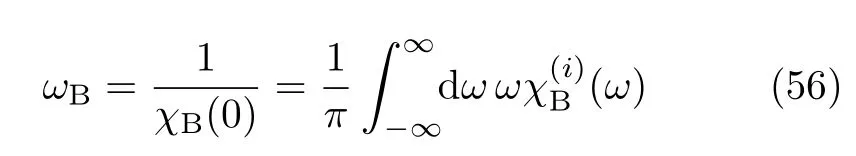
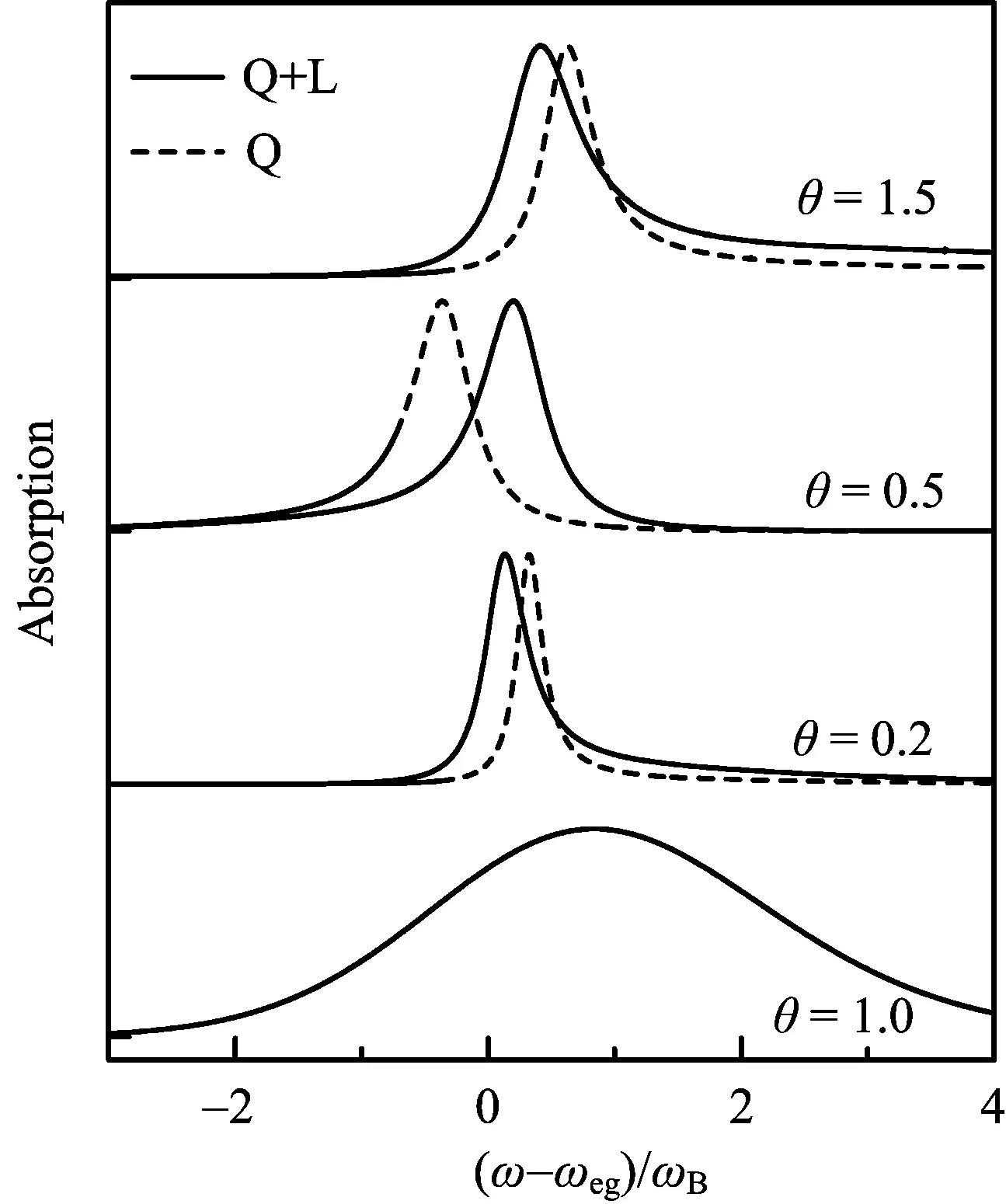
FIG.1 Evaluated absorption lineshapes.See text for the details.

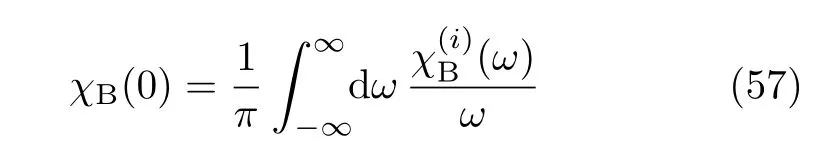
The above identities describe the determination of ωBvia any given χ(i)B(ω).Actually,Eq.(56)follows in line with the de finition of χB(ω)in Eq.(5).

For numerical illustrations,we adopt the Drude model for the secondary bath.The resultant χB(ω), which supports Eqs.(54)−(57),reads

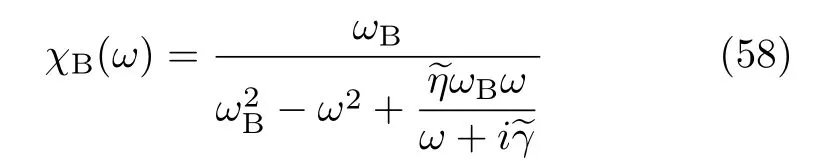
We set the parameters(in unit of ωB)andand also λ=1 for nonzero linear bath coupling strength.FIG.1 depicts the evaluated linear absorption spectra,at four representing values ofWhen θ=1 there is only the linear bath coupling.The other three(solid)curves with θ≠1 are of both the linear and the quadratic bath couplings,which are presented in parallel with their linear-free(thin) counterparts. In contrast with the pure linear bath coupling(θ=1)case,the spectrum lineshape is generally asymmetric.The observed skews in individual lineshape pro files,which show non-monotonic dependence on θ,are all in qualitative agreements with the secondary-bath-free but analytical results[27].

V.CONCLUSION

Evidently,the dissipaton algebra leads readily to the DEOM formalism.The key contribution of this workis the establishment of the generalized Wick’s theorem with a pair of dissipatons added;i.e.,the GWT-2,Eq.(13)and Eq.(14).The other ingredients of the dissipaton algebra had all been well established in our previous work[10,11].

The new ingredient,Eq.(13)and Eq.(14),which is now veri fied unambiguously,can be used consecutively to treat further higher-order nonlinear bath couplings.For example,the GWT-3,illustrated with the dissipaton-basis-set size of one,would go with[cf. Eq.(13)]

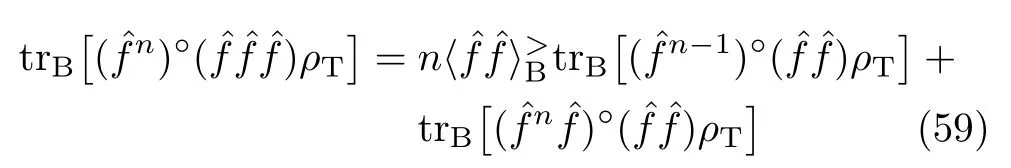
While the first quantity is evaluated by using Eq.(13) and Eq.(14),the second quantity would be

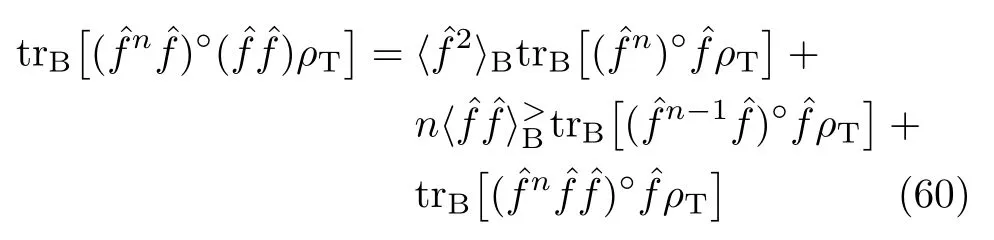
The first two quantities are evaluated via the GWT-1 and the GWT-2 of Eq.(14),respectively.The last quantity above goes with

The GWT-3 is then completed.The GWT-n follows the same recursive procedure.Thus,the present work represents a major advancement in the DEOM theory, with the speci fied class of non-Gaussian coupling environments that could be physically characterized,as illustrated in this work.

VI.ACKNOWLEDGEMENTS

This work was supported by the Ministry of Science and Technology of China(No.2017YFA0204904 and No.2016YFA0400904),the National Natural Science Foundation of China(No.21633006 and No.21373191), and the Fundamental Research Funds for Central Universities(No.2030020028).

APPENDIX A:The Smoluchowski limit:Conventional approach

This appendix utilizes the standard textbook approach of Ref.[22]to derive the extended Zusman Eq.(33).This is the application of the Smoluchowski limit to the Caldeira-Leggett’s equation(Eq.(24)),and derive the closed equation for

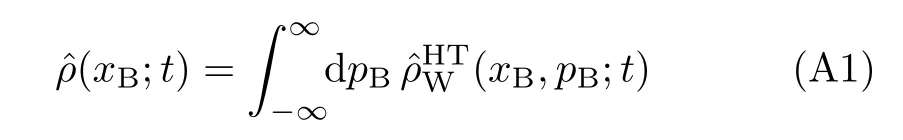
We start with the FP operator,Eq.(25),which has the coherent and incoherent contributions:

where

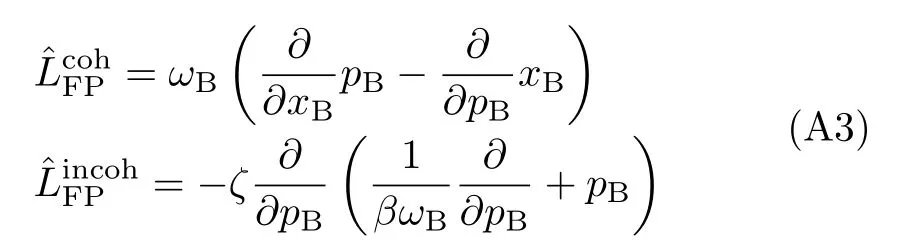
It is easy to obtain[22]

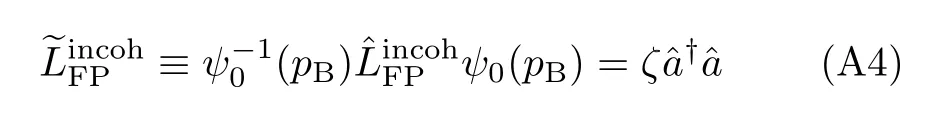
where

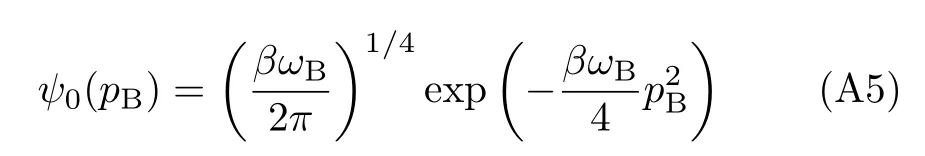
and

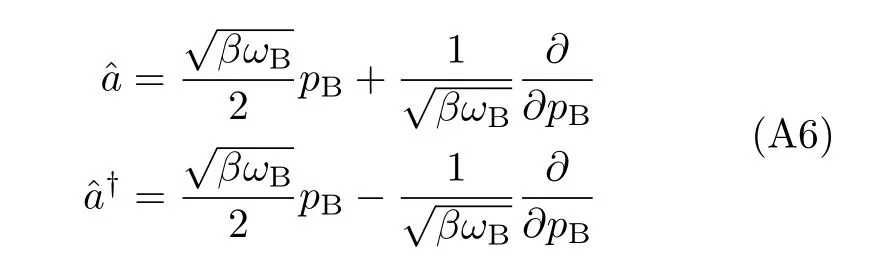
These are the bosonic annihilation and creation operators,satisfyingThe normalized eigen solutions to Eq.(A4)are therefore

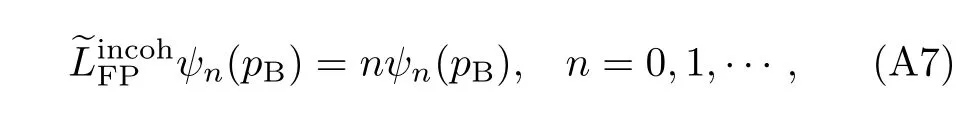
with the ground state ψ0(pB)of Eq.(A5)and

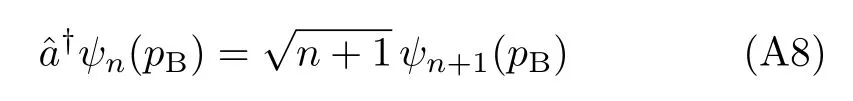
Apparently,{ψn(pB)}are all real.

On the other hand,from Eq.(A6),we evaluate

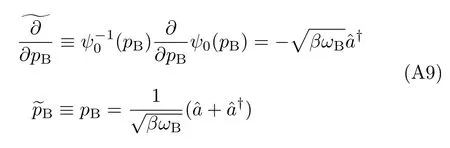
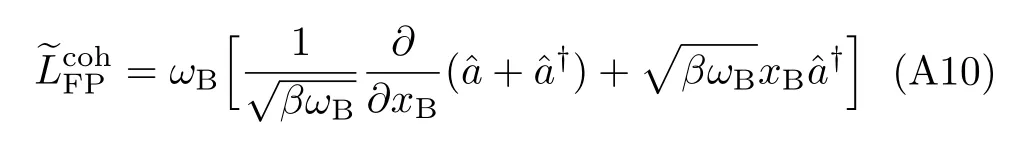
We have also

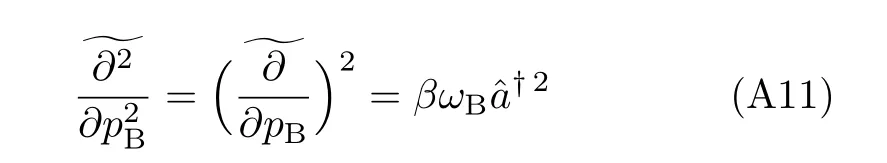
Turn now to the transformed Caldeira–Leggett’s equation(Eq.(24)),

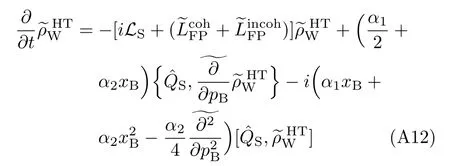
for

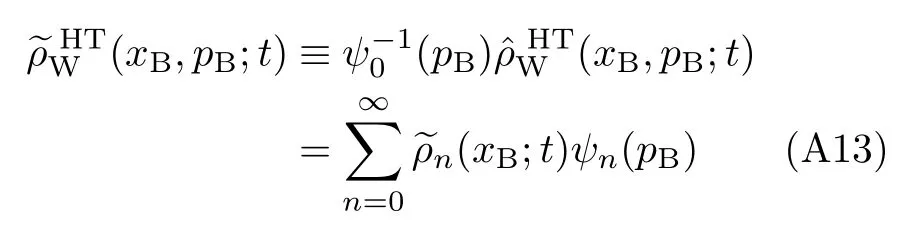
The second expression goes with the complete and orthonormal basis set of{ψn(pB);n=0,1,···}.Therefore,

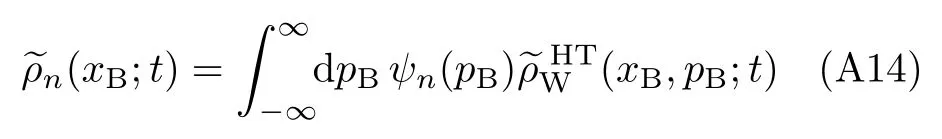
Together with Eqs.(A4)–(A11),we obtain

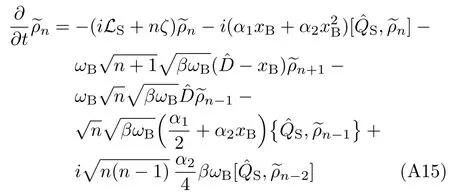
where

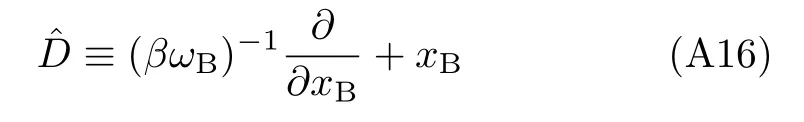
Consider now the Smoluchowski limit,where ζ≫ωB. To derive a single closed equation in this limit,it requires further[22](i)the core Hamiltonian,HS+,could be neglected compared to the friction,as the bath coupling is considered up to the quadratic level,cf. Eq.(A15).Consequently,while

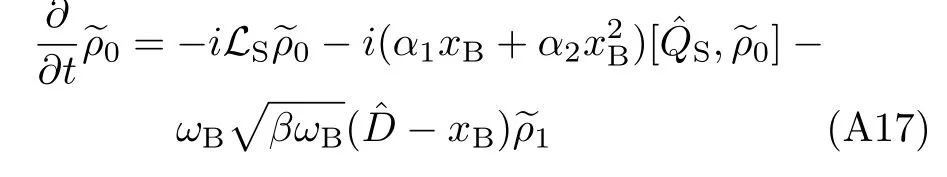
Eq.(A15)with n=1 and 2 becomes,respectively,

The latter two,together with Eq.(A16)and γ≡ω2B/ζ, result in

The second expression is obtained by considering the Smoluchowski limit where ζ≫ωB. Note also(cf. Eqs.(32)and(A16))

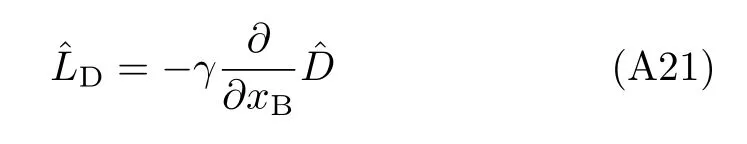
and(cf.Eq.(26))

The high-temperature relation is used here;see comments after Eq.(25).Substituting Eqs.(A20)–(A22)into Eq.(A17),followed by some simple algebra,we obtain

On the other hand,from Eq.(A1),Eq.(A13),and Eq.(A14),we have

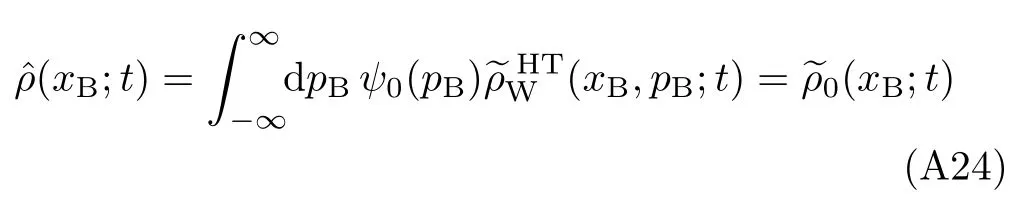
Therefore,Eq.(A23)is equivalent to Eq.(33). We have thus completed the standard Fokker–Planck–Smoluchowski approach[22]to the construction of the extended Zusman equation. Apparently,the novel method of construction,on the basis of Eqs.(27)–(29) that result in the rules of diffusion mapping,Eq.(30) and Eq.(31),is much simpler and physically more appealing.

[1]R.P.Feynman and F.L.Vernon Jr.,Ann.Phys.24, 118(1963).

[2]Y.Tanimura,Phys.Rev.A 41,6676(1990).

[3]Y.Tanimura,J.Phys.Soc.Jpn.75,082001(2006).

[4]R.X.Xu,P.Cui,X.Q.Li,Y.Mo,and Y.J.Yan,J. Chem.Phys.122,041103(2005).

[5]Y.A.Yan,F.Yang,Y.Liu,and J.S.Shao,Chem. Phys.Lett.395,216(2004).

[6]J.S.Jin,X.Zheng,and Y.J.Yan,J.Chem.Phys.128, 234703(2008).

[7]U.Weiss,Quantum Dissipative Systems,3rd Edn., Series in Modern Condensed Matter Physics,Vol.13, Singapore:World Scienti fic,(2008).

[8]H.Kleinert,Path Integrals in Quantum Mechanics, Statistics,Polymer Physics,and Financial Markets,5th Edn.,Singapore:World Scienti fic,(2009).

[9]Y.J.Yan and R.X.Xu,Annu.Rev.Phys.Chem.56, 187(2005).

[10]Y.J.Yan,J.Chem.Phys.140,054105(2014).

[11]Y.J.Yan,J.S.Jin,R.X.Xu,and X.Zheng,Frontiers Phys.11,110306(2016).

[12]U.Fano,Phys.Rev.124,1866(1961).

[13]A.E.Miroshnichenko,S.Flach,and Y.S.Kivshar,Rev. Mod.Phys.82,2257(2010).

[14]H.D.Zhang,R.X.Xu,X.Zheng,and Y.J.Yan,J. Chem.Phys.142,024112(2015).

[15]R.X.Xu,H.D.Zhang,X.Zheng,and Y.J.Yan,Sci. China Chem.58,1816(2015).

[16]H.D.Zhang,Q.Qiao,R.X.Xu,and Y.J.Yan,Chem. Phys.481,237(2016).

[17]H.D.Zhang,Q.Qiao,R.X.Xu,and Y.J.Yan,J. Chem.Phys.145,204109(2016).

[18]J.S.Jin,S.K.Wang,X.Zheng,and Y.J.Yan,J. Chem.Phys.142,234108(2015).

[19]A.O.Caldeira and A.J.Leggett,Physica A 121,587 (1983).

[20]A.Garg,J.N.Onuchic,and V.Ambegaokar,J.Chem. Phys.83,4491(1985).

[21]M.Thoss,H.B.Wang,and W.H.Miller,J.Chem. Phys.115,2991(2001).

[22]H.Risken,The Fokker-Planck Equation,Methods of Solution and Applications,2nd Edn.,Berlin:Springer-Verlag,(1989).

[23]H.D.Zhang,J.Xu,R.X.Xu,and Y.J.Yan,“Modified Zusman equation for quantum solvation dynamics and rate processes,”in Reaction Rate Constant Computations:Theories and Applications,edited by K.L. Han and T.S.Chu,Ch.13,RSC Theoretical and Computational Chemistry Series No.6,London,(2014). http://dx.doi.org/10.1039/9781849737753-00319.

[24]L.D.Zusman,Chem.Phys.49,295(1980).

[25]L.D.Zusman,Chem.Phys.80,29(1983).

[26]D.Y.Yang and R.I.Cukier,J.Chem.Phys.91,281 (1989).

[27]Y.J.Yan and S.Mukamel,J.Chem.Phys.85,5908 (1986).

∗Author to whom correspondence should be addressed.E-mail: yanyj@ustc.edu.cn