运城市城区土层剪切波速与埋深关系分析

霍魁 曾金艳 丁学文

(山西省地震局， 太原 030006)

运城市城区土层剪切波速与埋深关系分析

霍魁 曾金艳 丁学文

(山西省地震局， 太原 030006)

根据运城市城区地震小区化建设项目中72个土层的剪切波速测试资料，采用幂函数模型对粉土、粉砂、粉黏土、细砂的土层剪切波速与埋深进行加权回归分析，得到不同土类的模型参数及拟合优度指标。将土层剪切波速预测值与实测值进行对比，验证了回归关系式的合理性和适用性。土层剪切波速与埋深呈较好的幂函数关系，拟合优度均在0.9以上。

运城市城区； 土层埋深； 回归分析； 剪切波速

土层剪切波速是岩土地震工程中的一个重要物理量，在场地土类划分、地基饱和土液化判别、土层地震反应分析等方面得到了广泛应用[1-2]。通常采用现场原位测试方法确定土层剪切波速，现场原位测试方法分为单孔检层法、跨孔法和表面波法。其中，单孔检层法能直接给出土层的准确位置、厚度及波速，很少受测试场地环境限制，是目前应用最广泛的方法[3]。受土体本身固有的变异性及测试技术水平等影响，测试结果具有较大的变异性，误差甚至可能超过30%[4-5]。本次研究中，将利用实测土层剪切波速资料建立土层剪切波速的统计关系，并对统计估计值、现场实测值和土层特征进行对比分析，综合确定土层剪切波速值。

1 城区工程地质条件

根据土层剪切波速与埋深及其标准贯入值的相关研究[6-11]，可知：

(1) 除土层埋深外，影响土层剪切波速的因素还包括土质类别、形成条件、天然重度、物理性质等。

(2) 土层剪切波速与埋深的关系可通过线性模型、一元二次多项式模型、幂函数模型进行拟合。总体上，一元二次多项式或幂函数模型的拟合精度较高。

(3) 不同地区土层剪切波速与埋深的经验关系具有较大差异，表现出很明显的地域性。

(4) 以土层动力性质基本一致的工程地质单元为统计单元，可得到较好的土层剪切波速与埋深经验关系。

运城市城区主要建设规划用地位于具巨厚松散沉积物的断陷区，覆盖层厚度多为74～76 m。总体上来看，场地内第四纪松散层厚度较稳定，土层厚度变化明显受断裂控制：层序也比较稳定，地层比较连续，呈近水平状，不同时代地层为整合接触。覆盖层厚度涉及地层自上而下有第四系全新统、上更新统、中更新统地层[12]。

全新统沉降中心主要在运城市区以南的盐池一带，厚度为10～30 m，中条山北麓断裂和盐湖北岸断裂全新世时期活动强烈。岩性下部为深灰、灰绿色粉砂质黏土，上部为黑色粉砂质黏土，多呈淤泥状，并出现多层石盐晶体，湖积成因。盐池外市区全新统厚度约0～10 m，地层为褐黄色 — 浅黄色粉土，稍密，含白色菌丝、钙核，湖积成因；上更新统在盐池一带厚度约30～60 m，为一套灰绿色粉砂质黏土，具有水平层理，含有丰富的盐类矿物，呈沉积旋回，湖积成因。盐池外市区上更新统湖相沉积较薄，厚度约5～30 m，地层为褐黄色-浅黄色粉土、粉质黏土，稍密-中密，可塑，土质不均匀，含少量细砂、云母碎片；中更新统以河湖相地层为主，为湖相的粉砂质黏土、粉土层，浅灰、褐灰色，中密-密实，可塑，含少量细砂、云母碎片、锈斑点，偶见蜗牛壳。运城市城区土层水平范围内变化不大，垂直范围内结构简单，可作为一个工程地质单元，用于确定土层剪切波速与土层埋深的统计关系。

2 分析资料收集

本次工作中，收集了运城市地震小区化建设项目中72个钻孔，图1为工程场地位置分布图。从图中可以看出，场地均匀分布于运城市区主要建设用地规划范围，保证了本次工作统计结果的适用性。每个钻孔波速测试深度按《工程场地地震安全性评价》(GB 17741 — 2005)、《岩土工程勘察规范》(GB 50021 — 2001)等相关规范要求，达到假想基岩面。结合土层结构测点垂直间取2 m， 分析各数据测试点。选取72个钻孔和5个收集钻孔共2 160个测点的剪切波数据，各土类测试点深度间隔为10 m，其分布情况见表1。

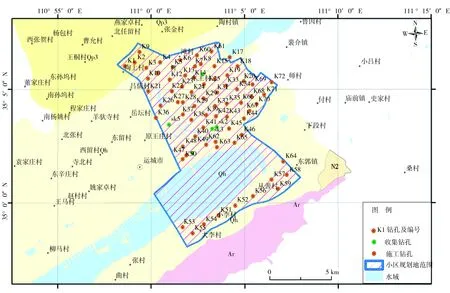
图1 运城市小区化工程场地位置分布示意图

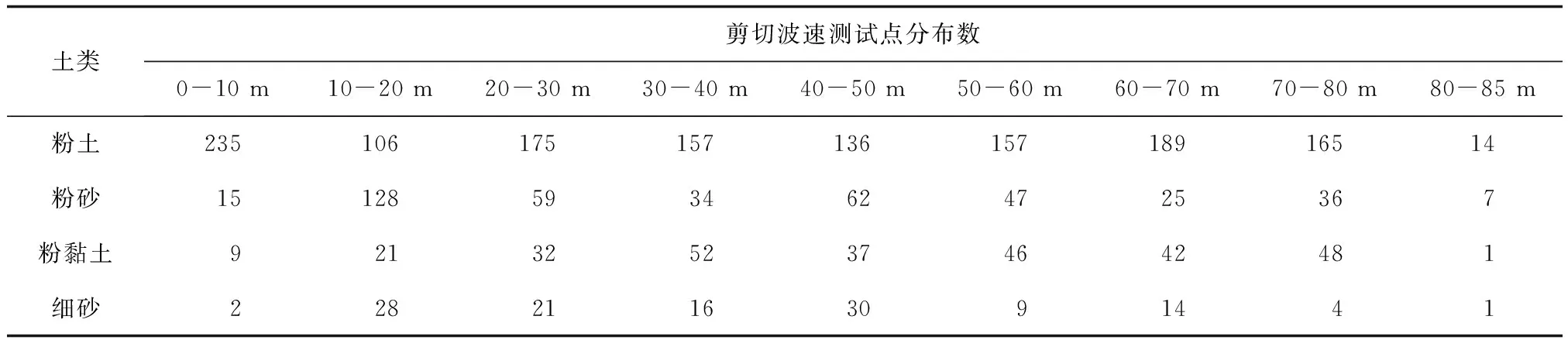
土类剪切波速测试点分布数0-10m10-20m20-30m30-40m40-50m50-60m60-70m70-80m80-85m粉土23510617515713615718916514粉砂151285934624725367粉黏土9213252374642481细砂22821163091441

3 回归分析

根据收集到的剪切波速测试资料，分别对粉土、粉砂、粉黏土、细砂进行了回归分析。首先绘制了各类散点图(图2)，从图中可以看出呈非线性规律，参照以往研究成果，采用幂函数模型Vs=a*Hb+c(Vs为剪切波速，H为土层埋深，a、b、c为回归系数)表示土层剪切波速与埋深的关系。

首先，以埋深分档样本数量的倒数作为加权平均数相对值wr；然后，为了估计剪切波速的变化，对加权系数进行标准化处理，即wn=wrmean(wr)；式中wn为向量平均值；最后，利用Matlab软件提供的nlinfit和nlpredci函数进行加权回归分析，分别计算出粉土、粉砂、粉黏土、细砂回归参数，判定系数R2、误差标准差及95%预测区间。图2中虚线表示95%预测区间，实线为预测函数Vs=a×Hb+c，式中各参数见表2。

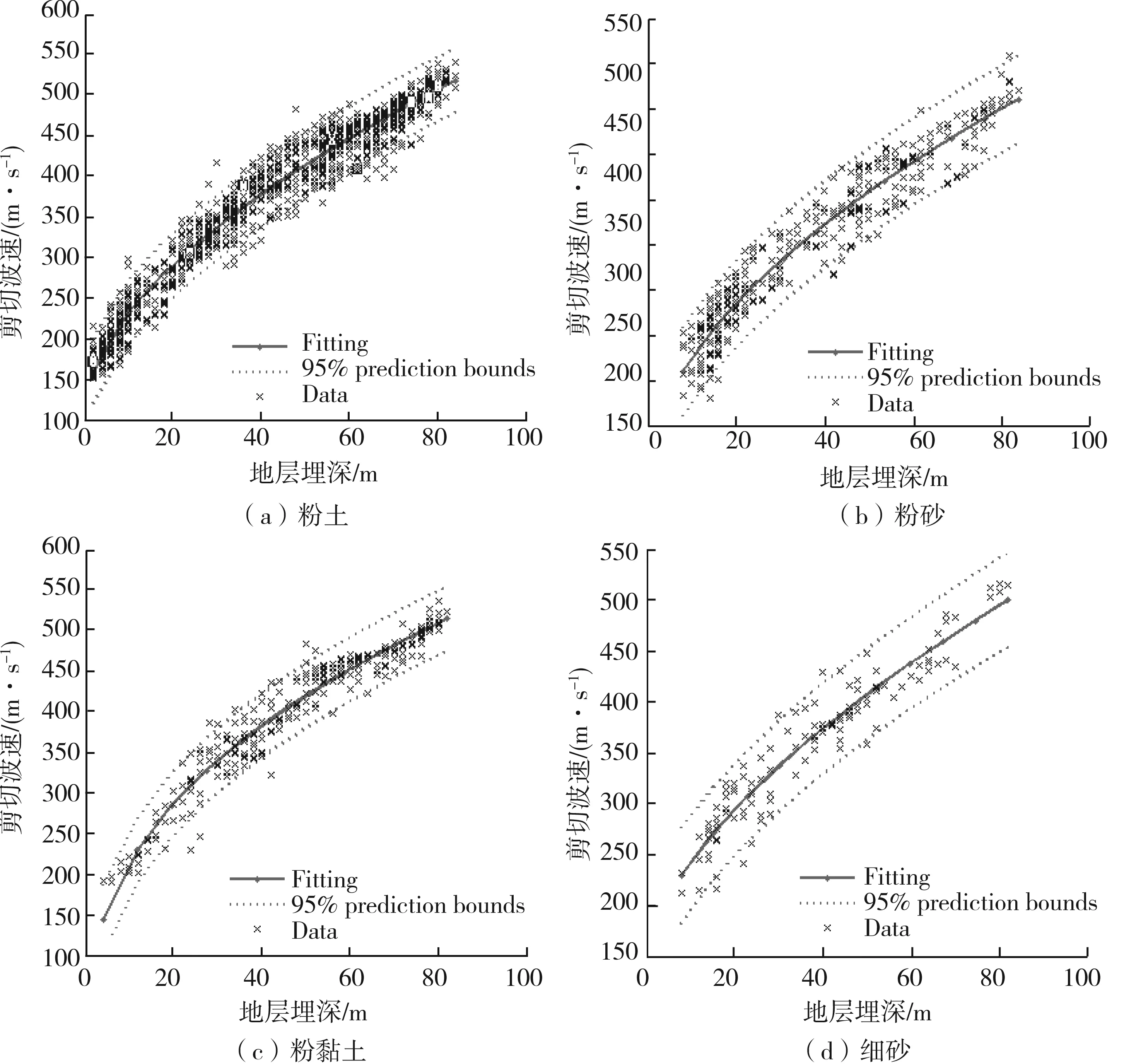
图2 土层剪切波速与埋深关系拟合曲线

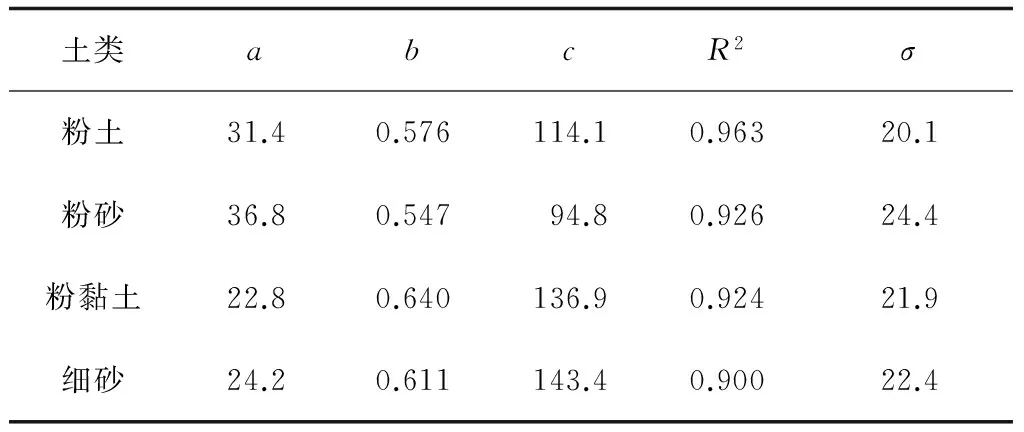
土类abcR2σ粉土31.40.576114.10.96320.1粉砂36.80.54794.80.92624.4粉黏土22.80.640136.90.92421.9细砂24.20.611143.40.90022.4

4 工程检验

选取运城市城区几个工程场地的钻孔，利用上述回归关系式进行剪切波速预测，计算其相对误差，验证所得关系式的预测精确度。具体对比结果见表3。可以看出，土层剪切波速推测值相对误差均小于7.8，15个测试点中只有4个测试点的相对误差超过了5%。这表明，此回归关系式可以较准确地预测该地区的土层剪切波速。

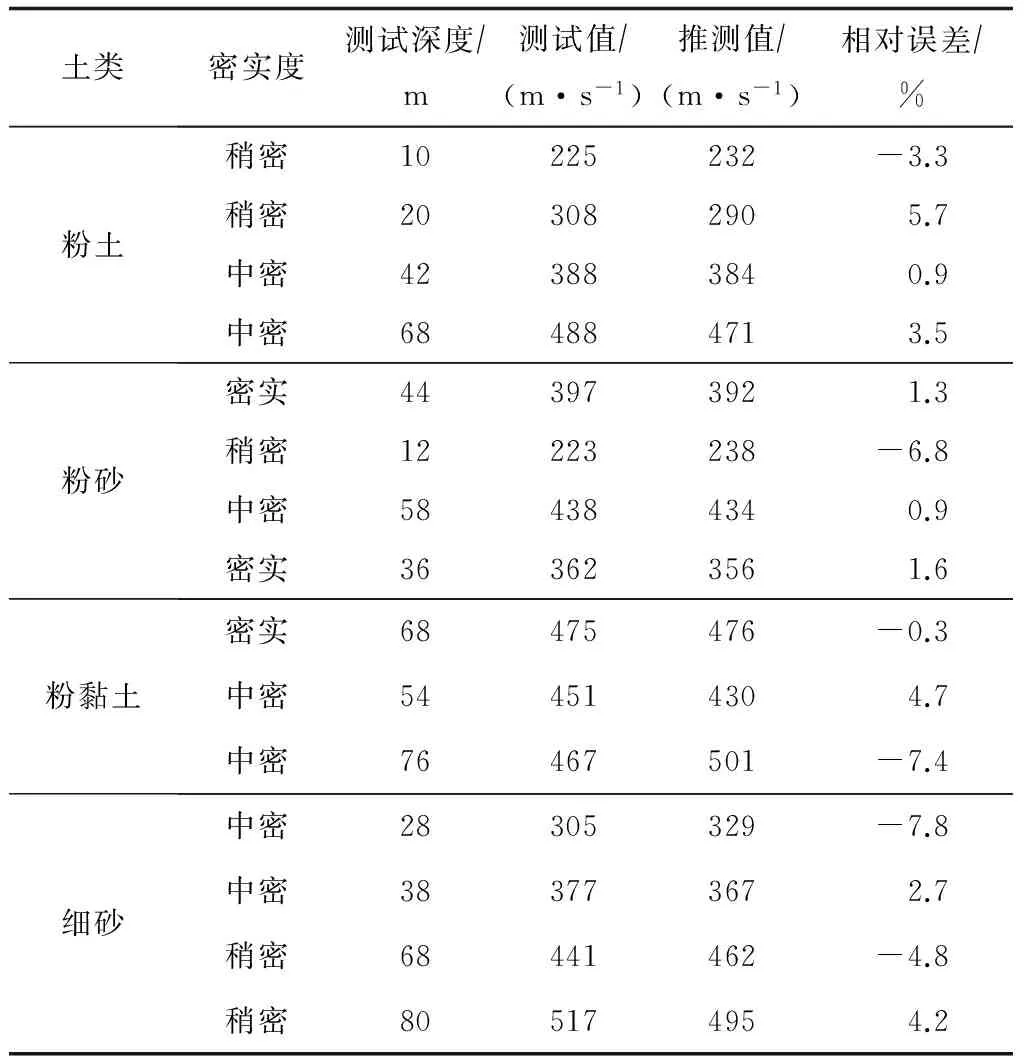
表3 土层剪切波速预测值与实际值对比

5 结 语

(1) 根据城区场地土层结构分析，认为城区土层结构相对简单，水平变化不大，可将其作为一个工程地质单元，并确定土层剪切波速与埋深具有关联性。

(2) 通过对回归方法和回归系数的显著性检验，得到幂函数模型Vs=a*Hb+c，可以较好地拟合出城区粉土、粉砂、粉黏土、细砂土层剪切波速与埋深关系。

(3) 通过某工程场地剪切波速实测值对比分析，认为本次所给出的回归公式可较准确地预测该地区土层剪切波速。

[1] 廖振鹏.地震小区划：理论与实践[M].北京：地震出版社，1989：5-12.

[2] 周锡元，王广军，苏经宇.场地·地基·设计地震[M].北京：地震出版社，1990:57-61.

[3] 汪闻韶.土工地震减灾工程中的一个重要参量：剪切波速[J].水利学报，1994，25(3)：80-84.

[4] 孙锐，刘红帅，刘德东.土体动力参数不确定性及影响研究[G].哈尔滨： 中国地震局工程力学研究所，2009：22-30.[5] 刘红帅，郑桐，薄景山，等.黏性土剪切波速不确定性的统计分析[J].世界地震工程，2010，26(增刊1)：99 -103.

[6] 李凡，李大华.天津软土剪切波速影响因素的灰色关联分析[J].勘察科学技术，2004(3)：9-11.

[7] 程祖锋，李萍，李燕，等.深圳地区部分岩土类型剪切波速与深度的关系分析[J].工程地质学报，1997，5(2)：163-168.

[8] 陈国兴，徐建龙，袁灿勤.南京城区岩土体剪切波速与土层深度的关系[J].南京建筑工程学院学报，1998，45 (2)：32-37.

[9] 李存志，李向新，姚明波.昆明盆地剪切波速与地基特性相关分析研究[J].昆明冶金高等专科学校学报，2006，22(3)：1-5.

[10] 齐文浩，刘德东，兰景岩，等.西安阎良区土层剪切波速统计分析[J].防灾科技学院学报，2008，10(4)：10-12.

[11] 张忠利，袁媛 ，罗云. 北海市土层剪切波速与埋深的关系[J].华南地震，2015,9(3)：40-45.

[12] 王乃樑. 山西地堑系新生代沉积与构造地貌[M]. 北京：科学出版社, 1996：206-217.

Relationship Between Soil Shear Wave Velocity and Soil Depth in Urban Areas of Yuncheng City

HUOKuiZENGJinyanDINGXuewen

(Earthquake Administration of Shanxi Province, Taiyuan 030006, China)

Based on data of shear wave velocities measured from 72 Yuncheng districts, the paper does the weighted regression analysis for shear wave velocity and depth of soils with various of soil type, including silt, silty sand, silty clay, fine sand, by using the power function model, and gets the model parameters of different soil types and goodness of fit index. Finally, the paper verifies the rationality and applicability of the regression equations via comparing measured values with the predicted values. The results show that there is power function relation between the sheaf wave velocities and the depths of soils in Yuncheng, and the goodness of fit is over 0.9.

Yuncheng City; soil depth; regression analysis; shear wave velocity

2017-05-02

山西省地震局科研项目“运城市土层剪切波速与埋深的关系”(SBK-1633)

霍魁(1987 — )，男，硕士，助理工程师，研究方向为岩土地震、强震台网。

TU411

A

1673-1980(2017)04-0112-04