“四有心人”催开数学教育之花
2017-09-03曾宪梅
文︳曾宪梅
“四有心人”催开数学教育之花
文︳曾宪梅

我大学读的是数学专业,觉得数学博大精深,它的神奇魔力就好比诺瓦列斯所说“纯数学是魔术家真正的魔杖”。数学的本质在于它的自由,人的心总是向往自由的美好。在数学学习里,我得到了这样的满足与宽慰。毕业后又与数学有缘,很荣幸成了一名小学数学老师。刚参加工作时,我认为小学数学容易教,自己有点大材小用,每天按照自己的理解进行教学,结果就是你在台上“激情四射、对牛弹琴”,学生在台下“漫不经心、目中无人”,往往在“怒火中烧”后师生两败俱伤。我觉得数学那么有趣,为什么学生却毫不领情呢?原来数学教育不只是单纯地传授数学知识,课堂教学不可能在一厢情愿中发生。我得努力去追求和谐的、幸福的数学课堂。非常神秘与高深的数学课堂,不用心岂能轻而易举就得要领?于是我每天认真阅读相关专业书籍,更重要的是扎根数学课堂教学实践,从一点一滴做起,改变正在悄然发生,我的数学教学迎来了温暖的春天。
精心挖掘教学内容
小学数学教材上的知识简单,练习题也容易,大部分孩子学有余力。如果仅仅教书本上的知识,按部就班地完成书上的练习题,对学生来说没有多大的挑战性。为了能够让学生体会到思维的乐趣,我们需要好好研读教材,创造性地使用教材,深入地挖掘教学素材。我在执教时,都会精心设计有层次、有思维含量的教学内容,让学生在学习中总能有新意,有收获。
人教版数学教材三年级上册中有一道这样的“年龄问题”(如图1所示)。学生很快就能解决这两个问题:(1)今年爸爸的年龄:6×6=36(岁)。(2)去年爸爸的年龄:36-1=35(岁),小丽的年龄:6-1=5(岁),爸爸的年龄是小丽的倍数:35÷5=7。

图1

图2
教学如果就此划上了句号,就不圆满了。还记得二年级上册教材中的年龄问题(如图2所示),我在处理这道题时,拓展到“两个人的年龄差不变”这样的深度。于是再次教学“年龄问题”时,我利用“两个人的年龄差不变”迁移出问题:两个人的年龄倍数会怎样?为什么?学生不假思索地回答:“两个人的年龄倍数不变。因为两个人的年龄差不变。”如此想来,这样的教学设计挺有意思。我继续质疑:“两个人的年龄倍数真的也不变吗?”学生满脸困惑,进而产生想办法求证自己想法的冲动。我及时引导学生通过表格列举进行验证。
爸爸比小丽大多少岁?
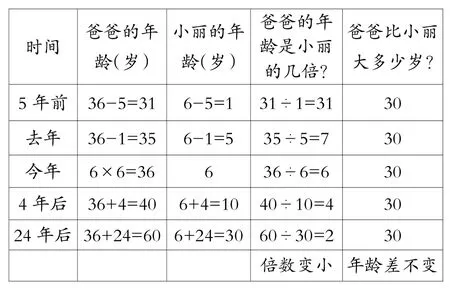
带着学生经历这样深入的研究过程,学生体会了科学解决问题的方法,并得出与自己猜想完全不同的结论:两个人的年龄倍数会越来越小。这也许就是数学常常给人的惊喜吧!可我并没有就此止步,而是趁热打铁:“爸爸年龄和小丽年龄的倍数越变越小,会小到1倍甚至更小吗?”学生再次脱口而出:“会。”在老师异样的神情中,学生这次变得更加慎重了,有的继续列举计算,有的开始讨论。不一会儿,一个孩子说:“不会小到1倍,因为爸爸永远比小丽大30岁,他们的年龄永远不会相等,倍数一定大于1。”此时孩子们恍然大悟。我顺势出示一组爸爸的年龄是小丽年龄倍数的数据:31、7、6、4、2、1.75、1.6、1.5……与1越来越接近。数学的魅力不用我多说,孩子们一定在这样的体验中刻骨铭心了。
真心地实现生本理念
《数学课程标准》提出“学生是学习的主人,教师是学习的组织者、引导者和合作者”。它的意图是要告诉老师们课堂教学中要尊重学生、理解学生、关爱学生,让教育像呼吸一样自然,让教育像春雨润物一样无声。
执教三年级“买票中的数学问题”一课,为了很好地实现生本教学理念,整节课我只给学生出示了一个问题情境:下表是植物园的票价。3位老师带50名学生去参观植物园,怎样买票最合算?

学生们先独立思考,写下自己的方法,然后在小组内进行交流,最后全班交流。3位学生主动板书了3种不同的购票方法:①分开买:3×10+5× 50=280(元);②全买团体票:53×6=318(元);③凑买一张团体票:(3+7)×6+(50-7)×5=275(元)。在比较中,学生得出第③种方法最合算。千金难买回头看,为了激励学生进行更加深入的研究,我提出挑战性的问题:“通过计算我们知道凑买一张团体票是最合算的,可我就是想知道都是买53张票,为什么凑买一张团体票会最省钱呢?”学生的思维马上就像开了闸的洪水般活跃起来。他们发现:如果成人买团体票就能省钱,儿童买团体票就会多花钱,只要比较成人节省的钱和儿童多花的钱的关系就能得出怎样买票最合算:①成人节省的钱>儿童多花的钱——凑买团体票;②成人节省的钱<儿童多花的钱——分开买;③成人节省的钱=儿童多花的钱——凑买团体票或分开买。在这样活泼、民主、自由的教学过程中,学生深刻体会了列举、比较、变与不变这些重要的数学思想与方法的内涵。每一位数学教师在课堂教学中都要给学生足够的时间与空间,把学习的主动权还给学生,在生本教育中点化和润泽生命。
尽心沟通数学与生活的联系
《数学课程标准》十分强调数学与现实生活的联系,要求“重视从学生的生活经验和已有知识中学习数学和理解数学”。因此,在教学中,我们必须架起数学与生活的桥梁,不但要把生活引进课堂,促其生活化,更要让学生带着数学走进生活,理解生活中的数学,体会数学的价值,促其数学化。
在“买票中的数学问题”一课的最后,我又让数学回归生活,就买票问题提问:“如果我不拿7位学生与3位老师凑买一张团体票,还可以怎样凑团体票?”在生活中,我们还可以找身边的7位陌生人一起凑买团体票,或者先买一个10人团体票,再把多余的票卖给别人或者去退票,50名学生都是买的学生票,不用多花钱,这样做还可以节省更多的钱。学生解决问题的数学方法与真实的生活经验再一次沟通对话,以至于下课时一位孩子说他这一节课的收获为:“以后我们学数学不能死记呆背,要灵活运用,不仅仅是为了考试,而是为了创造更加美好、幸福的生活。”全场听课的老师给孩子们致以最热烈的掌声,这也是对我本节课的教学最高的赞扬与嘉奖。数学到后来越来越抽象,离生活中的家长里短渐行渐远,只有当它回归生活、创新生活时才能凸显它的英雄主义,学生也会更爱数学。

倾心处理预设与生成
课堂教学难免会有未曾预料的情况发生,我们要根据教学目标做出机智处理,不能视而不见,也不能穷追不舍,恰如其分才是美。一堂课成也“课堂中学生的生成”,败也“课堂中学生的生成”,处理得好可以锦上添花,处理得不好就会弄得“满盘皆输”。把握好这个度也许要倾尽一生的精力,不断地反思总结。这也好比无限思想,没有完美的课堂,但我们可以努力去追求它,无限地逼近它,完美在路上,完美在心中。
在上二年级上册“排数”时,我让学生先独立思考:用1、2、3组成两位数,每个两位数的十位数和个位数不能一样,你能组成几个两位数?学生在汇报交流时出现了以下几种情况:
①12、32、23、21;
②12、21、13、31、23、32;
③12、13、21、23、31、32;
④21、31、12、32、13、23。
师生在对比辨析中总结:第①种方法有遗漏;第④种方法无序。于是我把黑板上的第①种、第④种方法擦掉,引导学生重点研究第②种和第③种,得出排数的一般方法:交换法(第②种)和固定法(第③种)。
②12、21、13、31、23、32;
④12、13、21、23、31、32。
在方法优化的过程中,我以为很尊重学生,让每个孩子都说了自己的想法,可快下课的时候,做出第④种方法的孩子很委屈地说:“老师,我用的方法也是固定法呀,我是固定个位,不信,您认真看看。”
②12、21、13、31、23、32;
③12、13、21、23、31、32;
④21、31、12、32、13、23。
我这时才恍然大悟,后悔上课时武断地擦掉了他的方法,应该给他发表自己想法的机会。幸好我最后让他在全班做了交流,弥补了预设的不足。有了它的生成,我的教学“更上一层楼”了,学生的思维也更加灵动了。
有一句话这样说:“只要用心做一件事,全世界都会帮助你。”我愿意用心做教育,把它当作我生命的事业用一辈子来爱它。任何一个教育工作者,只要用心去做教育,那么你的心一定会波澜壮阔。“心”比天高,比海阔,除了我文中所说的“精心、真心、尽心、倾心”这“四心”以外,应该还有很多诸如此类的“心”可以成就教育之美,比如“童心与爱心”。教育人应该有一颗童心,童心比爱心更重要。爱心需要培养,而童心只需要保持。可能因为多年的研究与实践,如今我的数学课堂已成了孩子们最喜欢的小天地,每次下课总有小粉丝围着我,要么向我提出数学难题公然挑战,要么公开表白我字写得太漂亮,要么渴盼我赶紧更新“有趣的数学故事”……通过自己的努力,我已催生了一丛数学教育之花。花开了,我愿更努力地做它们的护花使者,犹如那春天里勤劳的小蜜蜂:“不论平地与山尖,无限风光尽被占。采得百花成蜜后,为学生辛苦为学生甜。”
(作者单位:长沙市芙蓉区东郡小学)
