基于三维DLT理论的架空导线弧垂测量
2017-09-03郭军科王璋奇于香英
叶 芳,郭军科,田 锰,王璋奇,张 星,于香英
(1.国网天津市电力公司电力科学研究院, 天津 300384;2.华北电力大学 能源动力与机械工程学院, 河北 保定 071003; 3.天津市电力科技发展有限公司, 天津 300384)
基于三维DLT理论的架空导线弧垂测量
叶 芳1,郭军科1,田 锰2,王璋奇2,张 星2,于香英3
(1.国网天津市电力公司电力科学研究院, 天津 300384;2.华北电力大学 能源动力与机械工程学院, 河北 保定 071003; 3.天津市电力科技发展有限公司, 天津 300384)
架空导线作为电力系统的重要组成部分,肩负着传输电能的重要使命,弧垂直接影响输电线路的安全稳定运行。提出了一种三维DLT和二维DLT相结合的弧垂测量方法,采用三维DLT求解投影矩阵,然后运用二维DLT计算导线序列点的二维空间坐标。避免二维DLT方法标定点选取困难的问题,与三维DLT相比计算量大大减小。使用形态学方法处理导线边缘检测图像,避免出现双边缘和断裂现象,便于单根导线的提取。基于链码跟踪原理,提供了一种通过控制搜索方向在交叉情形下进行导线提取的方法。试验结果表明,在日常巡检时便可采用本文方法实现输电线路弧垂的快速测量,测量误差约为13 cm,具有较高的测量精度,且拍摄角度灵活、操作简单、成本低、效率高,具有重要的工程应用价值。
架空导线;弧垂测量;直接线性变换
0 引 言
电力系统是我国经济建设的基础,也是国民生活的重要保障。架空导线作为电力系统的重要组成部分,导线弧垂是输电线路设计和运行的重要指标,其合理性直接影响整个电力系统的安全稳定运行。弧垂过小,导线应力增加导致断线、断股和倒塔事故;弧垂过大,导致安全距离不够,出现放电现象[1,2]。此外,弧垂是限制架空导线输送容量的重要因素[3]。传统的弧垂测量方法有角度法、等长法和驰度板观测法等[4]。这些方法工作强度大、效率低,已不适应电网发展和科学管理的需求。
国内外许多学者对架空线路弧垂测量方法进行了多年的研究,出现了一些新的测量方法。文献[5,6]通过测量导线温度,结合输电线路状态方程进行测量,但传感器测量的只是导线表面温度,所以测量误差较大。Chris Menasha Bonus提出利用DGPS技术进行导线弧垂测量,该方法采用四个卫星定位Rover的位置,可以用于任意环境下架空导线固定点的弧垂测量。但是,这种测量方法的价格非常昂贵,功耗大[7]。美国EDM International,Inc.公司生产的Sagometer通过高精度图像,分辨导线上标靶的移动位置来测量弧垂[8]。美国The Valley Group Inc.公司生产的CAT-1通过测量导线应力来计算弧垂[9]。这些方法虽然在实际测量中取得了一定的成果,但是需要在导线上安装传感器,成本高,且不方便维护。文献[10]通过对部分段输电线图像的分析得到悬链段方法[11]的参数,进而确定导线的悬链线状态方程,并计算弧垂。这种方法简单方便,但需要在正视状态下采集图像,实际应用困难。文献[12]将导线间隔棒作为输电线特征点,并在航拍序列图像中进行图像匹配,然后采用计算机视觉方法计算特征点的空间坐标,最后拟合得到输电线的空间曲线。采用该方法测量弧垂时需要根据飞行器的飞行数据及GPS数据计算相机外参数,图像采集与相机外参数对应的时间存在时间差,引起不确定误差。
本文基于直接线性变换(DLT)理论提供了一种架空导线弧垂的图像测量方法。测量中只需要已知某些输电线路中铁塔的结构参数,然后对采集的图像进行分析处理,即可得到架空导线的弧垂参数。该测量方法可以在日常巡检时便可实现输电线路弧垂的快速测量,具有操作简单、成本低、效率高等优点,且很容易找到足够多的标识点,具有重要的工程应用价值。
1 架空导线弧垂测量原理
1.1 相机成像模型
相机成像模型是测量系统的重要组成部分,主要分为:垂直投影模型、弱透视成像模型、小孔成像模型等类型。其中小孔成像模型与实际情况最接近[13],所以本文选用小孔成像模型。
小孔成像模型原理如图1所示,空间点P的光线穿过光心O在投影平面的像点为p。空间点的相机坐标为(XC,YC,ZC),对应投影点的图像坐标为(x,y)。空间坐标系Ow-XwYwZw根据实际情况确定,用来描述空间点及相机的位置。

图1 小孔成像原理图Fig.1 Schematic diagram of pinhole imaging
图像像素坐标(u,v)是以图像左上角为原点的直角坐标系,u和v分别表示像素的列数和行数。图像物理坐标系o-xy是以光轴与投影图像交点为原点的直角坐标系,其x、y轴分别于图像像素坐标系的u轴和v轴平行。相机坐标系O-XCYCZC以相机的光心O作为原点,ZC轴与光轴重合,与成像平面垂直,取摄影方向为正方向,XC,YC轴与图像物理坐标x,y轴平行,且OO为相机焦距f。
1.2 DLT数学模型
直接线性变换是 Abdal-Aziz和 Karara 在 70 年代初提出的,主要用于图像校正与三维重建。直接线性变换是由像点、光心和空间点三点的共线方程得到的。
(1)
上式即为三维直接线性变换(DLT)的数学模型,Li为变换矩阵L的元素。由三维DLT模型可知,当空间场景中6个点坐标及其对应的像素点坐标均已知时,便可以对变换矩阵L进行求解。
DLT建立了图像坐标与空间坐标之间的转换关系,在计算时不需要相机的内参数和外参数,具有形式简单、求解稳定的特点。因此,特别适合用于非测量相机所拍摄图像的测量分析。
1.3 二维DLT数学模型
从三维DLT数学模型中可以很容易导出二维DLT的求解方法,设Z=0即可得到二维DLT数学模型:
(2)
由上式可知,二维DLT数学模型中只有8个未知量,而三维DLT数学模型中有11个未知量。所以,二维DLT所需要的标定点数量少,操作简单,计算量更小。
2 架空线序列点空间坐标计算
在进行空间点坐标的计算时,若采用二维DLT进行弧垂测量,则至少需要四个标志点。但是在猫头型、和酒杯型等杆塔中,很难在导线平面内找到具有明显特征的4个标志点。因此,本文对DLT算法进行了改进,首先采用三维DLT求解变换矩阵L,然后在计算架空导线空间坐标时进行降维处理,即将Z设为常数0,进而计算架空导线最低点弧垂。
与二维DLT算法相比,改进的DLT算法具有拍摄角度自由,在输电线路中很容易找到足够的标定点等优点,同时又避免了三维DLT算法计算量大的缺点。
2.1 变换矩阵求解
将式(1)变换为矩阵形式,有
(3)
当已知n个标志点的空间坐标及对应像点的像素坐标时,可得到2×n个方程:
(4)
其中,变化换矩阵表示为

(5)
为了计算变换矩阵L的11个未知数,需要至少已知6个标识点的空间坐标及对应的像素坐标。
2.2 物点空间坐标计算
本文对三维DLT算法进行改进,首先采用三维DLT求解变换矩阵L,然后在计算架空导线空间坐标时进行降维处理,即将Zn设为常数0,进而计算架空导线最低点弧垂。将式(4)进行处理后可得如下公式:
(6)
当已知投影变换矩阵及物点对应的像素坐标,可由下式计算该物点的空间二维坐标:
(7)

从杆塔中可以获得所需的标定点,方便起见,本文选取杆塔横担端点,在图2中用绿色“*”标记。至于导线序列点及导线挂点的像素坐标可以从图像中进行提取,由式(7)求得各点的空间二维坐标,此时便得到了架空导线的空间形态,进而可以对导线的各弧垂参数进行求解。

图2 标定点示意图Fig.2 Schematic diagram of calibration point
3 架空导线提取
3.1 架空导线图像的预处理
由于采集的图像易受光照等因素的影响,直接对图像进行特征提取的效果往往不理想,为了使输电线边缘特征的提取精度更高,需要对图像进行一定的预处理。这里的预处理主要包括滤波、边缘检测和膨胀腐蚀。
(1)图像滤波
在提取图像特征之前需要对图像进行滤波,以减小各种噪声的干扰和影响。本文采用中值滤波法,该算法在一定程度上避免了低通滤波造成的边缘模糊和高通滤波导致噪声增强的问题,且简单方便、易于实现。
(2)边缘检测
架空导线的提取可以归结为导线边缘的提取,本文采用Canny算子进行边缘检测,该算法对弱边缘和强边缘分别使用不同的阈值,因此错误率低,定位性高。但是,当图像分辨率较高时每根导线出现双边缘和断裂现象,且在两导线交叉位置出现“串线”的现象,如图3(b)所示。因此本文采用形态学方法进行处理,具体操作是,首先定义直径为2的圆盘结构元素,然后进行闭运算,处理前后效果如图3所示。图3(a)为经过形态学处理后的边缘检测图像,图3(b)、(c)分别为形态学处理前后导线交叉处的局部放大图。
经过形态学处理后,导线图像的双边缘、断裂现象以及“串线”现象消失,如图3(c)所示,为单根导线的提取打下了良好的基础。
3.2 基于链码跟踪的导线提取
链码跟踪是一种用来提取图像边缘点的提取方法,用具有一定长度和方向的连续线段来描绘图像的边界。常用的链码跟踪主要分为四向和八向两种,如图4所示,本文采用八向链码跟踪。
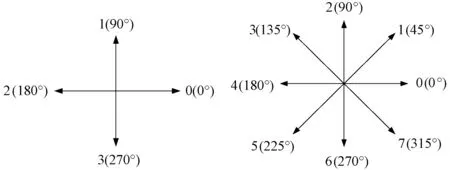
图4 四向和八向链码Fig.4 Four direction and eight direction chain code
在输电线路图像中,架空导线一般横贯整幅图像,不需要对每个方向进行搜索。因此,为了避免不必要的运算,只搜索八向中的2、1、0、7、6方向(起始点选择导线左端)。由于采集到的图像中会出现两导线交叉的现象,导线方向分为两种情形,情形一:向上,情形二:向下,如图5所示。针对两种情形,本文采用不同的搜索顺序,当方向向上时搜索顺序为:2、1、0、7、6;当方向向下时则为:6、7、0、1、2。此时在交叉处提取的导线会出现很小的偏离,但是对导线最低点弧垂的测量没有影响。

图5 导线交叉示意图Fig.5 Schematic diagram of cross wire
通过这种方法可以有效地判断导线的方向,进而实现单根导线的提取。在提取单根导线时,挂点附近的导线可能淹没在杆塔背景中,而这部分导线不影响测量结果,所以不必对该部分导线进行提取,只提取导线挂点即可。
具体实现步骤为:(1)手动选取导线起始点和终点;(2)判断导线方向;(3)从起点开始,按相应顺序搜索导线上的点,并记录各点坐标,直至终点;(4)手动选取导线对应的挂点,并记录其坐标。单根导线的提取结果如图6所示,图6(a)为架空线路原图像,示例中所提取的导线为图中所指的目标导线。图6(b)为单根导线的提取结果,绿色“+”标记为导线挂点,红色“x”标记为链码跟踪的起点和终点,导线挂点与链码跟踪起点、终点间的导线用红色直线代替。图6(c)为交叉处导线提取示意图,从图中可以看出该处提取的导线与真实情况不符,但是这段导线长度小,可以通过调节拍摄角度避免交叉情况出现在导线关键位置。由于使用形态学对导线边缘检测图像进行了处理,因此所提取的导线整体偏离了真实导线的中心。本文采用整体向下或向上移动所提取导线得到方法,将其移动到导线的中心轴处,移动像素值取计算目标导线纵向像素宽度的一半。

图6 单根导线提取结果Fig.6 Extraction result of single line
4 弧垂测量试验
4.1 试验研究
为了验证以上关于架空导线弧垂计算方法的可行性和精确度,本文进行了仿真试验。
试验对象选取现有等高悬挂110 V双回输电线路,建立的空间坐标系如图7所示。试验前使用经纬仪和激光测距仪测量了输电线路的相关参数,如各绝缘子挂点间的位置关系、档距、档距中央弧垂等参数,各测量值如表1所示。测量时,在红色“*”下方放置杆尺(该处为档距中央位置),使用本文算法计算该处导线的弧垂,试验测量数据如表2所示。
根据表1中的数据采用本文测量方法计算得到试验测量点及导线挂点的二维空间坐标,如表2所示。

图7 试验图像Fig.7 Experimental image

项目一号塔/cm二号塔/cm点1空间坐标(0,0,15)(16000,0,15)点2空间坐标(0,349 75992,60)(16000,349 75992,60)点3空间坐标(0,699 81701,15)(16000,699 81701,15)档距/m165中央弧垂/cm317

表2 输电线路参数计算值
经计算,图7中的试验测量点的弧垂为455.018 5-151.121 3≈304 cm,测量误差约为13cm,达到了实际工程中的要求。
此外,还使用本文算法计算得到了3.2.3节示例中所提取导线序列点的空间坐标如图8所示,通过这种方式计算得到导线最低点弧垂处的空间二维坐标为(8172.581 8,-455.825 7),该点对应的弧垂为455.825 7-151.121 3=304.704 4 cm,与单点测量的结果一致。因此,在实际测量中可首先采用本文方法计算导线序列点的空间坐标,然后实现架空导线的弧垂测量。

图8 架空导线序列点空间二维坐标Fig.8 Spatial coordinate of overhead line sequence point
由于拍摄方向与沿线方向的夹角较小,因此在图像远端塔附近很小一段距离在空间中对应的距离很长,因此图像采集时应该尽量正视拍摄。
4.2 误差分析
为了验证本文测量方法的可行性,选取了4.1节所示线路中17不同位置的弧垂进行了测量,最大误差不超过15 cm,达到了较高的精度。影响测量精度的因素主要包括以下几点:
(1)在使用经纬仪测量输电线路参数时引起的测量误差。
(2)标定点提取误差,由于图像分辨率有限,提取标定点像素坐标时不可避免会出现偏差,可以将图像放大后再提取标定点,以减小误差。
(3)相机畸变误差,在相机镜头生产装配过程中的误差,导致采集到的图像存在各种畸变,这会影响标定点像素坐标的精度。
(4)图像采集易受光照等不利因素的影响,应避免光照过强或过暗的情况。
5 结 论
(1)针对二维DLT测量方法的不足,提出采用三维DLT和二维DLT结合的测量方法,有效避免二维DLT方法标定点寻找困难的问题,与三维DLT方法相比,只需一张照片图像便可测量导线弧垂计算量大大减小。
(2)运用形态学方法处理边缘检测图像,可以消除导线图像的双边缘和断裂现象,便于提取导线。
(3)通过控制链码跟踪的搜索方向,实现了导线交叉情况下单根导线的提取。
(4)试验结果表明,测量结果与实际情况相符,试验测量误差不超过15 cm,具有较高的测量精度,达到了工程实际应用的要求。
[1] 裴玉龙.输电线路航拍图像处理及故障定位的研究[D].北京:华北电力大学,2011.
[2] 李俊芳. 基于计算机视觉的输电线路弧垂测量[D].北京:华北电力大学,2009.
[3] 王红斌,陈扬,高雅,等.输电线路弧垂对动态增容的影响[J].华北电力大学学报(自然科学版)2014,41(2):41-46.
[4] 赵新卫.线路弧垂的观测方法[J].技术应用,2009,(6):28-30.
[5] 王孔森,孙旭日,盛戈皞,等.架空输电线路导线弧垂在线监测误差分析及方法比较[J].高压电器,2014,50(4):27-34.
[6] 聂耸,程养春,戴沅,等.基于导线温度的架空线路弧垂新算法[J].华北电力大学学报(自然科学版),2013,40(6):27-32.
[7] MENSAH-BONSU C,KREKELER U F,HEYDT G T,et al. Application of the global positioning system to the measurement of overhead power transmission conductor sag[J]. IEEE Transactions on Power Delivery,2002,17(1):273-278.
[8] RAMACHANDRAN P,VITTAL V. On-Line Monitoring of Sag in Overhead Transmission Lines with Leveled Spans[J]. Power Symposium,2006. NAPS 2006,38th North American 17-19 Sept. 2006:405-409.
[9] 黄小龙.基于嵌入式图像处理的输电线弧垂在线检测系统研制[D].北京:华北电力大学,2015.
[10] 高强,文瑶.基于部分图像分析的输电线弧垂计算方法[J].电力建设,2010,31(11):38-42.
[11] 张震陆,陈本贤.柔索分析的“悬链段”方法研究[J].工程力学,1990,7(4):41-49.
[12] 仝卫国,李宝树,苑津莎,等.基于航拍序列图像的输电线弧垂测量方法[J].中国电机工程学报,2011,31(16):115-120.
[13] 黄增浩.基于双目立体视觉技术的导线脱冰跳跃轨迹监测研究[D].北京:华北电力大学,2016.
Sag Measurement of Overhead Lines Based on 3D Direct Linear Transformation Theory
YE Fang1, GUO Junke1, TIAN Meng2, WANG Zhangqi2, ZHANG Xing2, YU Xiangying3
(1. Electric Power Research Institute, State Grid Tianjin Electric Power Company, Tianjin 300384, China;2. School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China;3. Tianjin Electric Power Science and Technology Development Co., Ltd., Tianjin 300384, China)
As an important part of the power system, overhead lines play an important role in transmitting power. The sag exerts decisive effects on the transmission line operation. This paper proposed a method of sag measurement that combined three-dimensional direct linear transformation (DLT) and two-dimensional DLT. Three-dimensional DLT was applied to solve the projection matrix, and the two-dimensional space coordinates of the conductor point were calculated by two-dimensional DLT. This method can cope with the problem of selecting calibration points by using two-dimensional DLT method as well as reducing calculation compared with the three-dimensional DLT. In order to avoid double edge and fracture, this paper adopts morphological method to deal with the image of the conductor edge detection, and the single conductor is easy to extract by using this method. Based on the theory of chain code tracking, this paper provides a method of line extraction by controlling the direction of searching in the case of conductor crossing. The results of test show that the method proposed in this paper can rapidly measure sag in daily inspection, and the error is about 13cm, which is of high accuracy. In addition, this method is flexible to shoot and easy to operate with low cost and high efficiency, which is of great significance in engineering practices.
overhead lines; sag measurement; direct linear transformation
10.3969/j.ISSN.1007-2691.2017.04.11
2016-10-14.
TM73
A
1007-2691(2017)04-0071-07
叶芳(1986-),女,中级工程师,研究方向为输电线路工程、图像处理及计算机视觉。
