500kV 紧凑型线路导线脱冰跳跃计算分析

李 辉 梁盼望 侯长健

（中国能源建设集团湖南省电力设计院有限公司，湖南长沙410007）

0 引言

随着经济社会快速发展，输电线路走廊日益紧张，在路径走廊拥挤地区采用紧凑型输电方案具有巨大的社会效益和经济效益[1]，因紧凑型线路通过压缩导线相间距离来压缩输电线路走廊，因此存在相间距离小于常规输电线路的固有缺陷，导线脱冰跳跃后相间距离尤为紧张。因此，本文针对500 kV垂直排列双回紧凑型线路开展舞动不平衡张力计算，对铁塔进行安全校核，确保线路在舞动区的安全运行。

1 计算模型

1.1 边界条件

本文研究以500 kV紧凑型线路为例，气象条件为27 m/s，10 mm覆冰、15 mm覆冰、20 mm覆冰，导线采用等腰倒三角布置，如图1所示，顶部边长取6.7 m，腰长取7.2 m。

图1 导线布置方式

1.2 导线参数

500 kV紧凑型线路导线采用6分裂导线型式，考虑的导线型号如表1所示。

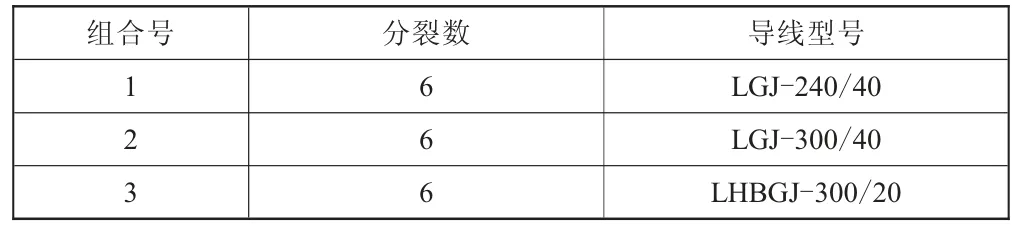
表1 导线分裂数及型号

1.3 导线相间最小空气间隙

根据《110 kV～750 kV架空输电线路设计规范》（GB 50545—2010）：海拔500 m以下，500 kV工频电压下，相对地的最小空气间隙为1.20 m。

则500 kV输电线路，导线相间最小空气间隙为：1.2×≈2.079 m。

根据《500 kV紧凑型架空输电线路设计技术规定》[2]（Q/GDW 110—2003），500 kV操作过电压下，档距中央的相间最小间隙取为3.85 m。

2 架空线路导线力学计算模型

架空输电导线的悬链线方程为（坐标原点取为悬链线的最低点）：

式中：σ0为导线最低点应力（MPa）；g为架空导线的比载（即单位长度导线所承受的载荷与导线截面积的比值，MPa/m）；l为档距（m）。

导线在不同气象条件A和B下的应力满足如下的状态方程式：

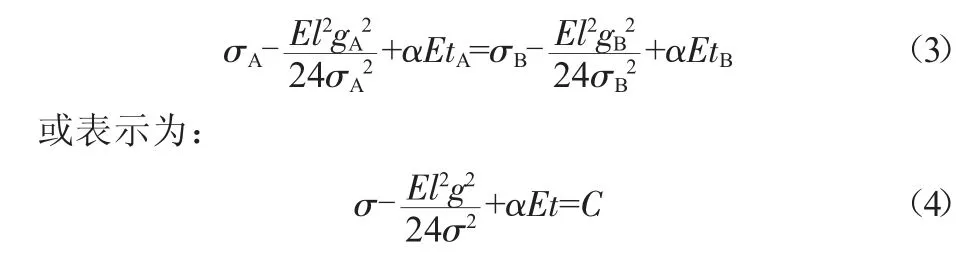
式中：E为架空导线的弹性模量（MPa）；l为档距（m）；g为架空导线的比载（即单位长度导线所承受的载荷与导线截面积的比值，MPa/m）；σ为导线应力（MPa）；t为温度（℃）。

3 导线脱冰动力计算

3.1 导线脱冰运动过程

覆冰脱落条件下导线动力计算，是模拟在设计覆冰的条件下（气温-5 ℃，风速0 m/s，覆冰厚度15 mm），初始状态三相导线均为100%覆冰，t=0时刻，下相导线（导线2）的全档覆冰的50%（以全部覆冰的冰重计）脱落，引起下相导线（导线2）跳起的动态过程。

3.2 脱冰时悬垂串摆动

设计覆冰不均匀脱落条件下，绝缘子串沿Z（导线走向）方向摆动。当架空输电线路的导线发生覆冰脱落时，除了覆冰脱落导线将向上垂直跳起外，由于覆冰量减小，导线张力将同时减小，将会导致悬垂绝缘子串两侧张力出现不平衡量，使悬挂点绝缘子串发生摆动，另一方面绝缘子串的摆动，将加大导线跳起的高度。

如图2所示，悬垂绝缘子串两侧分别连接相邻两档导线，在两侧导线张力的共同作用下达到平衡。当两侧导线的覆冰状况发生变化时，两侧导线的张力也发生变化，悬垂绝缘子串沿Z方向摆动，直至达到新的平衡。

图2 悬垂绝缘子串的受力及平衡

根据受力平衡原理，导线悬挂点处所受合力为0，即两侧导线张力及绝缘子串的拉力的总合力为0，可得：

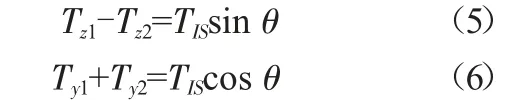
式中：TIS为绝缘子串的拉力（N）；θ为绝缘子串与垂直方向的偏转角。

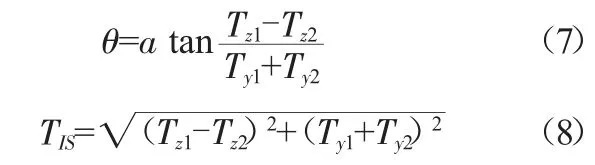
3.3 连续档导线脱冰计算模型

为了准确分析覆冰脱落情况下的导线运动规律，有必要建立多档导线模型。如图3所示，考虑2N+1档的导线模型，2N+1档导线为一个耐张段，两侧由耐张串悬挂，内部档间由悬垂串悬挂。

假定多档导线模型中，各悬挂点间无高差，且假设串1～N及N+2～2N+1共2N档的档距均为400 m，第N+1档为脱冰档，档距为300～1 000 m。

4 计算结果

导线不同脱冰率下脱冰跳跃计算结果如表2、表3所示。

由表2、表3计算结果可见：

（1）导线发生覆冰脱落后，由于不平衡张力，导线及悬垂绝缘子串将会发生Z向偏移。

（2）3种型号导线LGJ-300/40、LGJ-240/40、LHBGJ-300/20，在相同的覆冰脱落条件下，大档距时，就最大跳起高度而言，LGJ-300/40小于LGJ-240/40，LGJ-240/40小于LHBGJ-300/20，即LGJ-300/40抗脱冰跳动性能最好。

（3）两种脱冰工况，严重程度排序为：50%覆冰瞬时脱落＞25%覆冰瞬时脱落。

图3 多档导线模型

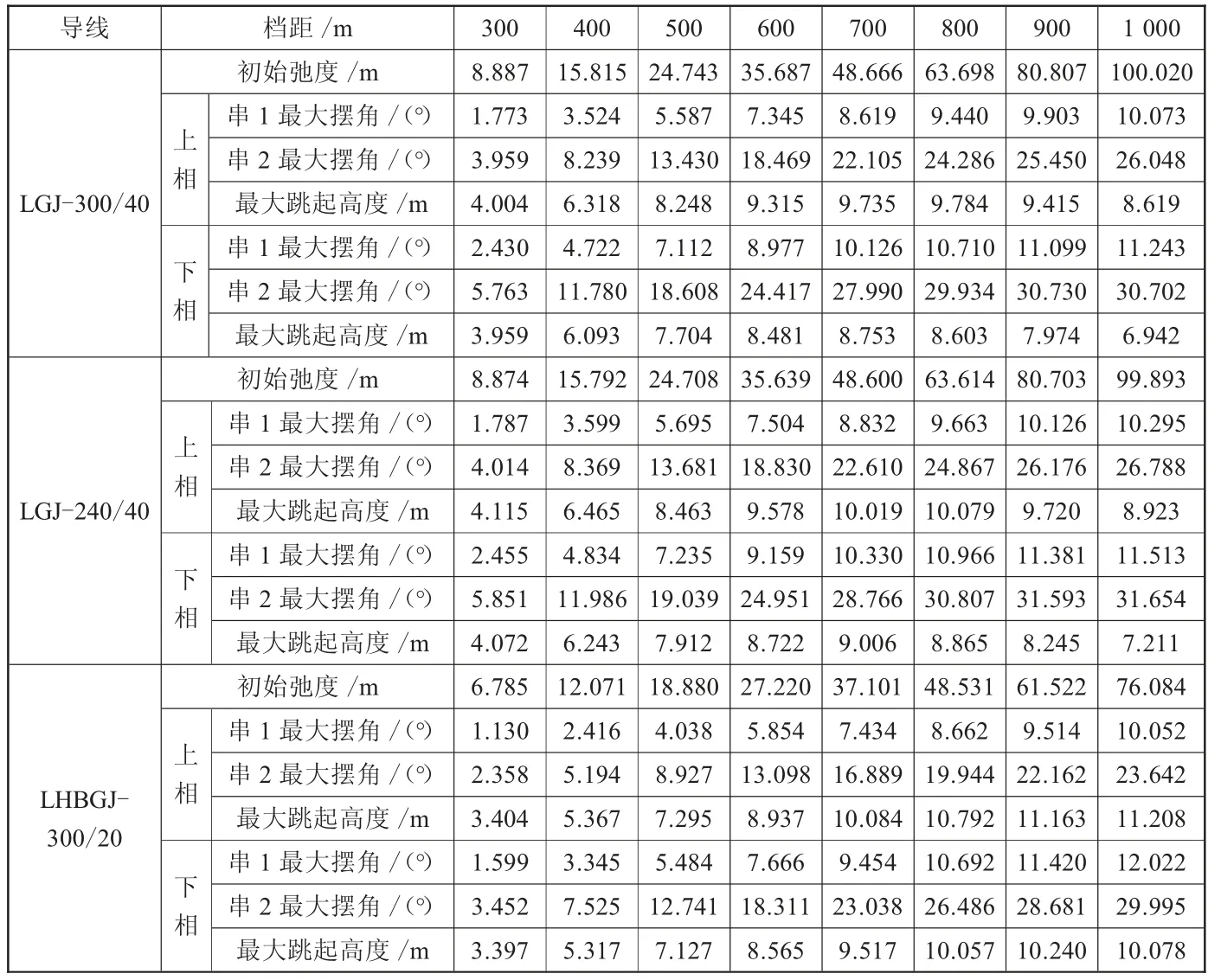
表2 50%覆冰瞬间脱落的动力计算结果（5档）

表3 25%覆冰瞬间脱落的动力计算结果（5档）

5 结语

本文针对500 kV紧凑型线路开展导线脱冰跳跃计算分析，结果表明，导线发生覆冰脱落后，由于不平衡张力，将会使导线及悬垂绝缘子串发生偏移，不同导线的脱冰跳跃特性存在一定差异，脱冰率越高，脱冰跳跃越严重。