多机电力系统TCSC新型自适应backstepping鲁棒控制
2017-09-03孙丽颖
赵 岩,孙丽颖
(辽宁工业大学 电气工程学院,辽宁 锦州 121001)
多机电力系统TCSC新型自适应backstepping鲁棒控制
赵 岩,孙丽颖
(辽宁工业大学 电气工程学院,辽宁 锦州 121001)
将含TCSC (Thyristor Controlled Series Compensation) 的多机电力系统等值为两机系统,在考虑参数不确定性和外部干扰的情况下,基于backstepping方法,结合浸入和不变(I&I)自适应控制、自适应滑模控制以及L2干扰抑制理论,设计了一种新型的非线性自适应鲁棒TCSC控制器。该TCSC控制器不仅对不确定参数具有较强的自适应能力,而且可以有效地抑制外部干扰对系统的影响。另外,把虚拟控制量的导数看作不确定项,应用滑模项补偿其不确定性,来避免backstepping方法中存在的“系数膨胀”问题。仿真结果表明,所设计的TCSC控制器具有较强的鲁棒性和自适应性,可以保证区域互联电力系统的静态和暂态稳定性。
浸入和不变自适应控制;backstepping方法;TCSC; 鲁棒控制;多机电力系统
0 引 言
现代电力系统通过区域互联取得较好的经济效益的同时,也给电网的稳定运行带来了新的挑战。自从柔性交流输电系统(Flexible Alternating Current Transmission System,FACTS)被美国学者N. G. Hingorani提出以来,越来越多的FACTS设备已经在电网的稳定控制中得到应用[1-3]。其中,晶闸管控制串联电容补偿技术(Thyristor Controlled Series Compensation,TCSC) 作为柔性交流输电设备之一,可以既经济又高效地提高电力系统的输电能力[4]。
有关TCSC稳定控制器的研究,学者们大部分是将实际的电网等效单机-无穷大(SMIB)系统,所采用的控制方法主要有:反馈线性化方法[5]、最优预测控制[6]、神经网络控制[7]、模糊控制[8]、鲁棒控制[9]、backstepping方法[10]等。然而,把大电网看成单机-无穷大系统进行研究已不能较好地模拟其动态特性,因此有必要致力于研究含TCSC的多机电力系统,本文将研究含TCSC的两区域四机电力系统。至今,多机电力系统TCSC稳定控制器的研究也已经取得了一定的成果[11-13],其中文献[12,13]都是基于自适应back-stepping方法,并没有考虑backstepping方法的“系数膨胀”问题。对于“系数膨胀”问题,目前主要应用以下方法,包括:动态面控制[14]、非线性跟踪微分器[15]、自适应滑模控制[16]等。其中,文献[14]和[15]采用的方法需要额外引入滤波器或微分器,这使控制器的设计过程更加复杂。相比之下,文献[16]的方法具有明显的优势,该方法不仅设计过程简单,而且具有较强的鲁棒性。综上所述,本文将基于backstepping方法,结合文献[16]提出的自适应滑模控制,设计一种效果较理想的互联电力系统TCSC控制器。并且,一方面,在设计不确定参数的自适应律时,采用浸入和不变(I&I)自适应控制[17],使自适应估计律更接近真实值;另一方面,考虑外部干扰对控制器的影响,对其应用L2干扰抑制理论,是控制器具有更好的鲁棒性。
本文将针对含TCSC的两区域四机电力系统模型,在含有不确定参数和外部干扰的条件下,基于backstepping方法,并结合浸入和不变(I&I)自适应控制、自适应滑模控制以及L2干扰抑制理论各自的优势,尝试设计一种非线性自适应鲁棒控制规律。最后,通过大、小干扰两种情况进行仿真研究,仿真结果表明:所设计的TCSC控制器对干扰有很强的鲁棒性,对不确定参数的估计值更接近真实值。
1 系统模型
图1为含TCSC的两区域四机电力系统,区域A和区域B通过弱联络线L7-9连接,其中,TCSC被串联在弱联络线的中点。区域内的发电机G1和G2以及G3和G4的电气联系紧密,并且受到扰动后动态行为类似,故我们可以将每个区域等值为一台发电机,即区域A、B分别被等值为E1∠δ1和E2∠δ2,则等值两机系统如图2所示[18]。

图1 含TCSC的两区域四机电力系统模型Fig.1 Two-area four-machine system with TCSC

图 2 含TCSC的等值两机系统Fig.2 Equivalent two-machine system with TCSC
在设计控制器时,做如下假设:发电机采用隐极机,且模型选用经典二阶模型;发电机采用暂态电抗使暂态电势E1和E2恒定;输入机械功率Pm1和Pm2恒定;考虑系统阻尼和外部干扰的影响;则可以建立系统的数学模型为
(1)
式(1)中,等值发电机的参数见表1,其中(i=1,2)。

表1 等值发电机参数
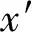
那么,弱联络线的有功功率为
(2)
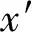
令Δδ12=δ1-δ2-δ0,Δω12=ω1-ω2。则,由式(1)和式(2)可得
(3)
假设θ=-D/H=-D1/H1=-D2/H2[20],则系统(3)中的Δ转化为
定义系统的状态变量为x1=Δδ12,x2=Δω12,选择控制变量u=1/(XTCSC+Xac)。则式(3)可变为
(4)
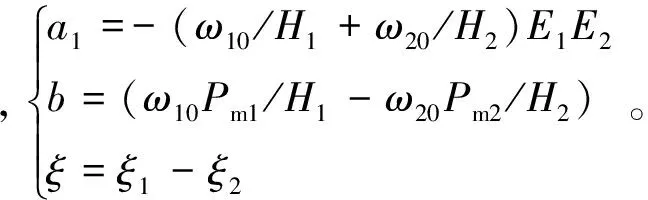
式(4)的调节输出取为z=[q1x1q2x2]T,其中,q1和q2为不小于零的权重系数,满足条件:q1+q2=1。其中,第一项q1x1的作用是使系统的功角差保持稳定,第二项q2x2可保证系统的转速差稳定。
注:本文研究的系统模型为:两区域四机电力系统。然而,对于更为复杂的网状网络(即多台发电机接在网状网络时),根据文献[18]可以把电气联系紧密且受扰后动态行为类似的发电机划分为一个区域,转化为两区域互联电力系统进行研究。
2 控制器设计
对于式(4),基于backstepping方法进行TCSC自适应鲁棒控制器的设计,需考虑两个原则,即(a) 当ξ=0时,可得到闭环系统是渐近稳定的; (b) 当ξ≠0时,先构造Lyapunov函数V(x),再递推设计反馈控制律u,使系统(4)对供给率:S=γ2‖ξ‖2-‖z‖2有耗散性,即令
(5)
在T>0时式(5)成立,使系统(4)的L2增益小于γ,其中,γ为干扰的抑制常数。
控制器的设计过程如下:
首先,定义如下误差滑模面:
(6)
式中:x2d为虚拟控制量。
Step1:由式(6)可知,s1的导数为
(7)
从式(7)可以看出,s2与状态变量x2有关,需要进一步地设计才能获得,因此把s2当作不确定项进行处理[16],并给出假设1如下:
假设1: 令‖s2‖≤α1,其中α1是未知且有界的正常数[16]。
取虚拟控制量x2d为
(8)
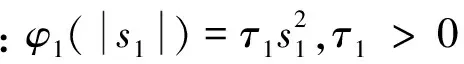
(9)
式中:ρ1>0 为自适应增益系数。
取Lyapunov函数为
(10)
其中,σ>0为一设计常数。
则V1的导数为
(11)
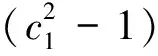
(12)
Step2:由式(6)可知,s2的导数为
(13)
扩展Lyapunov函数为
(14)
式中:ρ2>0为自适应增益系数。

(15)
其中,

取反馈控制量u为
(16)

(17)
然后,使用I&I自适应控制设计参数θ的自适应估计律。
令估计误差p为
(18)
对式(18)求导,得
(19)

(20)
将式(16)、(17)和(20)代入式(15)中,有
(21)
根据文献[21]可知:
(22)

(23)
令V(x)=2V2(x),则有
(24)
因为式(23)通过积分运算可变为耗散不等式(5),所以系统对干扰ξ是具有L2增益的。则,闭环系统的误差滑模面动态为
(25)
根据LaSalle’s定理[22]可知:对于系统(4),在反馈控制律(16)的作用下,闭环系统(25)是渐近稳定的,即当t→∞时,s1→0,s2→0。由x1、x2、x2d的定义知,x1收敛到0,x2也是有界的。

3 仿真研究
为了检验新型TCSC自适应鲁棒控制器的效果,通过MATLAB软件,选用图1所示的含TCSC的两区域四机电力系统模型进行仿真。发电机参数见文献[23],其他仿真数据如下:
小干扰仿真情况:假设在t=0时,发电机G1与G3的功角差δ130受到扰动后从15°突变为20°。仿真结果见图3和图4。
大干扰仿真情况:假设t=0.5 s时,输电线路L7-9中发生三相短路故障,0.1 s后切除故障。仿真结果见图5和图6。
下图中,NNARC-I为本文提出的新型非线性自适应鲁棒控制(NovelNonlinearAdaptiveRobustControl);NNARC-II为不考虑k类函数的情况;Ab为自适应backstepping方法。
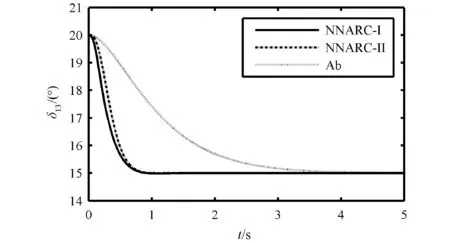
图 3 G1-G3相对功角响应曲线Fig.3 Response of G1-G3 power angle
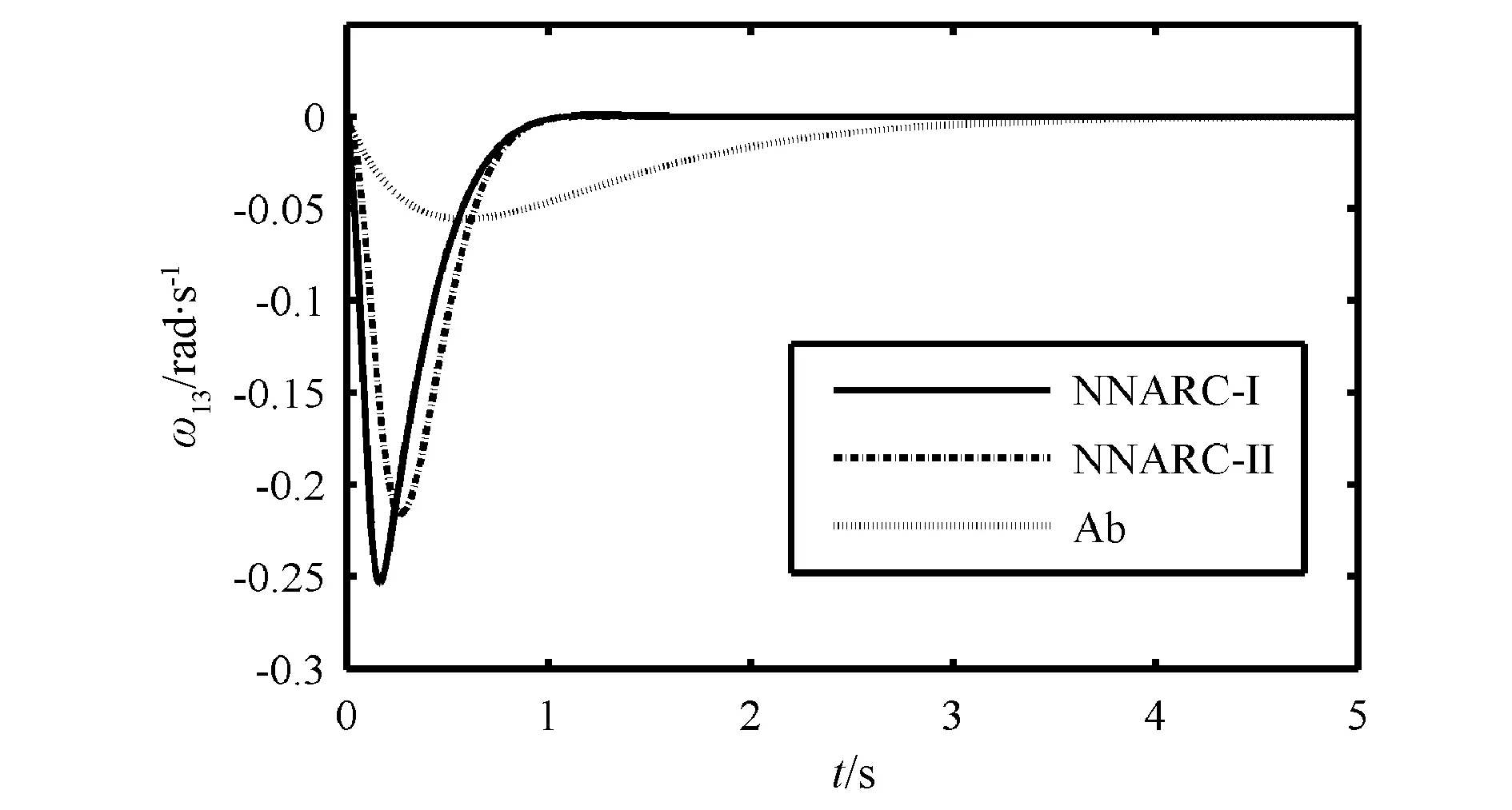
图 4 G1-G3相对转速响应曲线Fig.4 Response of G1-G3 rotor speed

图 5 G1-G3相对功角响应曲线Fig.5 Response of G1-G3 power angle

图 6 G1-G3相对转速响应曲线Fig.6 Response of G1-G3 rotor speed
从仿真图3至图6可以得出:相比Ab控制器,NNARC-II控制器对系统受到的大、小扰动都具有较强的鲁棒性,使故障时间缩短了大约75%,可以减少一定的经济损失。当系统受到大扰动时,NNARC-II控制器的超调量变得更小,曲线收敛速度更快了。另外,考虑k类函数作用的NNARC-I控制器在没有增加控制器设计复杂性的前提下,加快了系统趋于稳定的速度,减小了曲线的振荡范围,而且可以避免暂态响应和控制器增益之间的失衡。

图 7 参数θ的自适应估计律比较Fig.7 Comparison of adaptive estimators of θ
为了对比I&I自适应控制和传统自适应控制的自适应能力,给出了图7所示的仿真图。通过计算,我们知道参数θ的真实值为-0.46。从图7的仿真结果可以明显看出:I&I自适应控制设计的自适应估计律几乎等于参数θ的真实值,具有更强的自适应能力。
4 结 论
本文将含TCSC的两区域四机电力系统等值为两机系统,考虑阻尼系数的不确定性和外部干扰,基于backstepping方法,并结合浸入和不变(I&I)自适应控制、自适应滑模控制以及L2干扰抑制理论各自的优势,设计了一种新型的互联多机电力系统TCSC控制器。通过I&I自适应控制设计了参数θ的自适应估计律,增强了控制器的自适应能力。本文还采用自适应滑模控制处理了backstepping方法中存在的“系数膨胀”问题。仿真结果表明,所设计的TCSC控制器对干扰具有很强的鲁棒性,且对不确定参数的估计值更接近真实值。另外,由于该算法设计过程简单且效果显著,很容易推广到其他类似电力系统这种存在不确定参数和外部扰动的系统。
[1] 孙丽颖,冯佳昕,赵军.STATCOM的非线性鲁棒控制器设计[J].东北大学学报(自然科学版),2009,30(4):466-470.
[2] 殷婷,王杰.Lagrange力学在含TCSC电力系统Hamilton实现中的应用[J].电网与清洁能源,2013,29(12):30-35+49.
[3] 雷邦军,费树岷,翟军勇,等.静止无功补偿器(SVC)的一种新型非线性鲁棒自适应控制设计方法[J].中国电机工程学报,2013,33(30):65-70+11.
[4] 刘婷,井元伟,姜囡,等.TCSC系统的自适应minimax干扰抑制控制器设计[J].控制与决策,2013,28(12):1894-1897.
[5] 郑旭.基于反馈线性化的TCSC非线性PID控制[J]. 电力自动化设备,2006,26(9):86-88.
[6] 蒋铁铮,陈陈,曹国云.TCSC非线性最优预测控制器的设计[J].继电器,2005,33(20):45-48+72.
[7] 李志民,韩绪鹏,孙勇,等. 可控串联补偿的神经滑模控制器设计[J].电力系统及其自动化学报,2010,22(1):101-105.
[8] 解建宝,宁联辉,张靠社,等.可控串联补偿的非线性模糊PID控制[J].西安理工大学学报,2006,22(4):386-389.
[9] 孙丽颖,赵军.TCSC的自适应鲁棒H∞控制[J].东北大学学报(自然科学版),2008,29(1):13-16.
[10]ZHANGChao,ZHANGHang,LIJungang,etal.BacksteppingsildingmodecontrolofnonlinearTCSCSystembasedonadaptiveobserver[J].JournalofDiscreteMathematicalSciencesandCryptography,2015,18(1-2):157-175.
[11] 王宝华,邹德虎.TCSC自适应Terminal滑模稳定控制器设计[J].电力系统及其自动化学报,2011,23(4):111-114.
[12] 王宝华,杨成梧,张强.多机系统TCSC逆推鲁棒控制器设计[J].电工技术学报,2005,25(1):108-111.
[13] 朱林,蔡泽祥,兰洲,等.TCSC鲁棒自适应控制器的非线性逆推设计[J].控制理论与应用,2007,24(3):385-390.
[14]SWAROOPS,HEDRICKJK,YIPPP,etal.Dynamicsurfacecontrolforaclassofnonlinearsystems[J].IEEETransonAutomaticControl,2000, 45(10):1893-1899.
[15] 甄红涛,齐晓慧,夏明旗,等.四旋翼无人机鲁棒自适应姿态控制[J].控制工程,2013,20(5):915-919.
[16] 朱凯,齐乃明,秦昌茂.BTT导弹的自适应滑模反演控制设计[J].宇航学报,2010,31(3):769-773.
[17]ASTOLFIA,ORTEGAR.Immersionandinvariance:Anewtoolforstabilizationandadaptivecontrolofnonlinearsystems[J].IEEETransactionsonAutomaticControl, 2003, 48(4):590-606.
[18] 顾卓远, 汤涌, 孙华东,等.区域电网内弱联机群摆动对互联系统功角稳定性的影响[J].中国电机工程学报,2015,35(6):1336-1343.
[19] 屠竞哲,张健,王建明,等.大规模直流异步互联系统受端故障引发送端稳定破坏的机理分析[J]. 中国电机工程学报,2015, 35(21):5492-5499.[20] 卢强,梅生伟,孙元章.电力系统非线性控制(第二版)[M].北京:清华大学出版社,2008.
[21] 张蕾,张爱民,韩九强,等.基于系统浸入和流形不变自适应方法的静止无功补偿器非线性鲁棒自适应控制方法[J]. 控制理论与应用,2013,30(1):1-7.
[22] KHALIL H K.Nonlinear system [M].Third Edition.Beijing:Publishing House of Electronic Industry, 2011.
[23] KUNDER P.Power system stability and control [M].New York,USA:McGraw-Hill,1994.
NewAdaptiveBacksteppingRobustControlforMulti-machinePowerSystemwithTCSC
ZHAOYan,SUNLiying
(SchoolofElectricalEngineering,LiaoningUniversityofTechnology,Jinzhou121001,China)
The multi-machine power system with TCSC is equivalent to the two-machine system. With the consideration of parametric uncertainties and external disturbance, a new nonlinear adaptive robust TCSC controller is designed based on the backstepping method and combined with immersion and invariance (I&I) adaptive control, adaptive sliding mode control andL2interference suppression theory. The TCSC controller not only has well adaptive ability to the uncertain parameters, but also can effectively restrain the influence of external disturbance on the system. The derivative of the virtual controller is taken as an uncertain term, the uncertainty is compensated by the sliding mode term aiming at avoiding the “coefficient expansion” problem in the backstepping method. The simulation results show that, the designed TCSC controller has better robustness and self-adaptability, which can ensure the static and transient stability of the regional interconnected power system.
immersion and invariance (I&I) adaptive control; backstepping method; TCSC; robust control; multi-machine power system
10.3969/j.ISSN.1007-2691.2017.04.07
2016-10-09.
辽宁省自然科学基金项目(2015020076).
TM
A
1007-2691(2017)04-0044-06
赵岩(1992-),男,硕士研究生,研究方向为电力系统稳定性分析与控制;孙丽颖(1972-),女,教授,硕士生导师,研究方向为电力系统稳定性分析与控制。
