基于dSPACE双层隔振试验及其仿真研究
2017-09-03何其伟高伟鹏
黄 驰,何其伟,高伟鹏,苏 航
(海军工程大学 动力工程学院,武汉 430033)
基于dSPACE双层隔振试验及其仿真研究
黄 驰,何其伟,高伟鹏,苏 航
(海军工程大学 动力工程学院,武汉 430033)
由于控制系统中控制器输出到误差信号之间存在功率放大器、作动器以及误差传感器等,误差通道可能会使信号的幅值和相位发生改变,甚至改变信号的频率。运用FxLMS自适应控制算法,基于误差通道离线辨识,进行控制系统的仿真。基于dSPACE半实物仿真系统搭建试验平台,完成单频和双频信号的自适应主动控制,取得显著控制效果。
振动与波;Fx LMS;离线辨识;dSPACE
水下航行器因其隐蔽性和机动性,在现代战场上有着巨大威慑力。但是在水下航行器内部,各种动力机械产生的低频机械振动与噪声所引起的水下声辐射具有明显的线谱特性,严重影响其隐蔽性。传统的被动隔振对高频振动效果明显,但对低频振动的隔振效果很不理想。近年来,随着电子器件的微型化和数据处理的快速化,主动控制成为国内外专家研究的重点。其原理为通过传感器采集振动信号,然后通过作动器产生一个与振源信号幅值、频率相同、相位相反的信号来抵消振动信号,其对低频振动有着较好的控制效果。由于振源信号的时变性,需要对控制参数保持更新以确保控制效果[1]。
振动主动控制中,控制算法处于研究的核心地位。自适应控制可通过实时监测被控对象和扰动激励,实时更新控制参数以保持系统性能指标的最优。自适应控制可分为自适应滤波控制、自校正控制等。其中,自适应滤波控制在振动控制领域应用较多[2]。应用最广泛的是前馈FxLMS(filtered-x least mean square)算法。该方法基于均方性能函数最小化,寻优性能函数最小值,实现振动抑制。自适应前馈控制主要以滤波自适应前馈控制为主,还包含自适应前馈抵消方法(adaptive feedforward cancellation,AFC)等[3],文中采用FxLMS算法。
dSPACE是一套由德国dSPACE公司开发的控制开发及半实物仿真系统,其用虚拟控制器对实物进行控制,可以排除大多数早期设计中引入的错误和缺陷;用实际控制器对虚拟对象进行控制,可以模拟真实条件下进行的极端实验,缩短实验周期和费用。因为其在设计上的便利性,在机器人仿真如腕关节仿真器的开发和控制系统研究如挖掘机的挖掘环节控制等方面都有广泛运用。
采用FxLMS算法与dSPACE控制器相结合的控制平台,在保证稳定性的前提下调整滤波器的参数,控制器采用simulink对其编程,完成数据采集、数据处理、系统参数辨识、控制等一系列操作,提高控制速度,并在双层隔振实验台架上进行实验,取得不错的控制效果。
1 误差通道和FxLMS算法
1.1 误差通道
实际控制中,控制器输出信号y()n到误差信号e(n)之间存在功率放大器、电线、传感器等仪器,这些因素可能会使信号的幅值和相位产生变化,即误差通道。为了获得误差通道的传递函数,将横向滤波器作为误差通道的未知模型,根据滤波器的输入输出信号和辨识算法对横向滤波器的权向量进行迭代更新,使其不断逼近最优解。将此时滤波器的加权系数S()
z作为误差通道的辨识参数,虽然结构和参数不尽相同,但是其具有相同的输出特性。此时误差通道的计算公式变为

1.2 FxLMS算法
将标准的LMS算法用于主动控制系统很可能造成系统不稳定,这是由于次级通道传递函数S(z)的存在,使得参考传感器的信号与误差传感器的信号在时间上不对等。有两种方法来解决这一问题[4]。第一种是将S(z)的倒数1/S(z)置于误差反馈回路与S(z)串联,这样S(z)的影响被抵消;第二种方法是在参考传感器到LMS算法的权值更新之间加入S(z)的估计,这样人为给参考信号加入延时使得二者在时间上对等,这就是FxLMS算法。对于第一种方法,由于s(n)的倒数可能不存在,从而无法实现,因此FxLMS算法是一种更为有效的方法[3]。
图1是FxLMS主动控制算法的系统图,在k时刻的误差信号可以表示为

FIR滤波器的输出控制量为

其中w(k)为滤波器在k时刻的N×1阶加权系数向量,x(k)为N×1阶参考信号向量。

图1 基于滤波Fx-LMS算法的主动控制系统
在振动主动控制系统中,滤波器输出的控制信号不是所需要的直接控制量,它还需要经过误差传感器和控制器之间的误差通道得到,权向量s()k可表示为

由表达式

则误差传感器的输出可以写成

误差信号的平方近似均方差为

权值系数矩阵的梯度为

权值系数的更新公式为

其中μ为收敛系数
2 双层试验系统的建模与仿真
2.1 双层试验系统建模
如图2所示,M1、M2分别为被隔振设备质量和中层隔振平台质量,k1、k2分别为上下层隔振器刚度,c1、c2分别为上下层隔振阻尼。f0、f分别为振动激励力和主动控制力,y、ẏ 、ÿ、x、ẋ、ẍ分别为被隔振设备和中层台架的位移、速度和加速度。

图2 控制平台简化图
由此可建立如下动力学方程

拉氏变换后,令F0s=0、Fs=0可获得位移x与主动控制力f和激励力f0间的传递函数,具体如下所示

2.2 仿真
基于辨识得到的初级通道与误差通道的估计模型,建立simulink试验模型,并在计算机上进行单频激励信号的控制仿真。效果见图3、图4、图5。
从仿真结果可以看出,该主动控制系统对40 Hz、100 Hz、150 Hz三个频率的单频激励振动有着明显的隔振效果。误差信号收敛速度快,稳态误差小,表明了自适应控制算法的有效性和辨识准确性。在40 Hz的激励振动仿真时,采用300阶的滤波器,最小均方算法步长为10-4,效果明显,但是在100 Hz和150 Hz的仿真时,出现了收敛速度变慢,稳态误差变大的问题,这是由于滤波器阶数和步长设置不当造成的。在系统稳定的前提下,步长决定了算法的收敛速度和稳态误差,阶数反映了计算的复杂程度。减小步长和阶数,都会使控制效果减弱。前者会减小收敛速度,但减小稳态误差;后者可减小计算的复杂程度[5]。所以,经过计算,取128阶的滤波器和10-5的步长可以取得良好的仿真效果。
3 实验
3.1 试验台架搭建
图6为被控对象,中层隔振板四个角各有一个自主研发设计的主被动一体化电磁隔振器,此隔振器底层的橡胶充当了被动隔振设备,下层橡胶亦可简化为弹簧阻尼系统,详见图7,所以该被控对象可整体简化为弹簧-阻尼双层隔振实验平台,以中层隔振平台的加速度信号作为振动控制的评价指标。

图3 40 Hz单频激励控制效果图

图4 100 Hz单频激励控制效果图

图5 150 Hz单频激励控制效果图

图6 双层隔振平台实物

图7 主动隔振用作动器和下层隔振橡胶

图7 初级通道辨识
被控对象为双层隔振平台,振源为上层的作动器,由dSPACE输出参考信号到上层作动器,经功率放大器驱动作动器。控制器为dSPACE半实物仿真系统,由MIT和Hewlett-Packard Labs合作研发,以内容管理发布为设计目标,可以采集、存储、索引、保护和重新发布任何数字格式和层次结构的研究数据,与Matlab、Control Desk等软件配套使用。
在Simulink中设计FxLMS控制算法,配合控制器输出信号和中层加速器传感器测得的误差信号,以白噪声作为控制器输出信号,进行误差通道的离线辨识。用FxLMS算法计算出控制器输出电流的大小,经直流电源供给的功率放大器驱动中层主被动一体化作动器,减小中层隔振平台的加速器。
3.2 初级通道与误差通道的离线辨识
误差通道激励信号为随机白噪声,通过实际误差通道得到理想的输出信号,通过横向滤波器得到实际输出信号,将两者叠加产生的误差信号反馈到辨识算法中,完成横向滤波器的权向量叠加。此时的权向量即是误差通道的传递函数[6]。
图7为初级通道的辨识结果,图8为误差通道的辨识结果。

图8 误差通道辨识
在试验中初级通道的辨识采用600阶横向滤波器,误差通道的辨识采用700阶横向滤波器,辨识结果良好。
3.3 单频激励和双频激励主动控制试验
在仿真取得不错效果的基础上,进行单频和双频激励控制的实验台架试验,将Simulink中的数据输入输出用一件接口替换,保留逻辑关系和控制模块至ConrtolDesk,将传感器对应相应的输入输出,将150 Hz的激励信号作为振源进行输入,进行单频控制试验,将55 Hz和155 Hz的混合激励信号作为振源进行输入,进行双频控制试验。效果图见图9、图10、图11、图12。
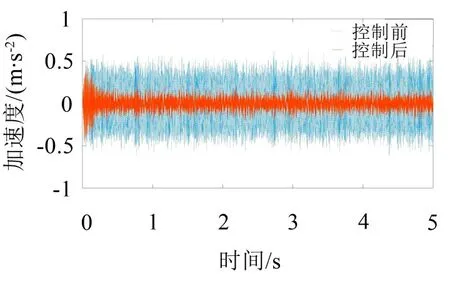
图9 单频激励控制前后误差信号

图10 单频激励控制前后频谱图
由试验结果可见,控制后的误差信号相较于控制前有较大减弱,在频谱图上(见图10)可以看见,控制后的线谱幅值有极大下降,降噪幅度达到近25 dB,隔振效果良好。
由试验结果可见,控制后的误差信号相对于控制前的误差信号有明显减弱。图12为双频激励控制前后的频谱图,在未开启主动控制前,其55 Hz和155 Hz两根线谱十分明显,在开启控制之后,两根线谱振动基本被完全抑制,降噪幅度达到20 dB。

图11 双频激励控制前后误差信号

图12 双频激励控制前后频谱图
4 结语
主要介绍了基于dSPACE的双层隔振试验平台,研究了FxLMS算法和Simulink编程仿真。文中首先推导FxLMS算法的理论公式,在Simulink中进行单频激励仿真,效果良好,并对滤波器阶数和迭代步长对控制性能的影响进行讨论。在双层隔振试验平台中进行单频和双频隔振试验。单频隔振试验中对150 Hz的激励信号隔振效果良好,双频隔振试验中对55 Hz和155 Hz两根线谱控制效果明显,基本实现了隔振平台的自适应控制,为下一步的研究奠定了基础。
[1]陈丽萍.振动主动控制技术的研究进展[J].现代机械,2005(2):35-39.
[2]高伟鹏,何其伟,闫政涛.一种应用FxLMS算法的双层隔振试验装置[J].噪声与振动控制,2016,36(4):70-75.
[3]齐海超.基于LMS自适应滤波算法的振动主动控制仿真软件开发及实验研究[D].哈尔滨:哈尔滨工程大学,2012.
[4]朱石坚,何琳.船舶机械振动控制[M].北京:国防工业出版社,2006.
[5]KUO S M,MORGAN D R.Active Noise Control:A Tutorial Review[J].Proceedings of the IEEE,1999,87(6):943-973.
[6]ESHGHI M,BOROUJENY S G,JALALI A.A hardware design for an online active noise control system[C]//MED'07.Mediterranean Conference on Controland Automation.IEEE,2007:1-5.
Test and Simulation of Double Layer Vibration Isolation Based on dSPACE
HUANG Chi,HE Qi-wei,GAO Wei-peng,SU Hang
(Power Engineering College,Naval University of Engineering,Wuhan 430033,China)
Since there are power amplifiers,actuators and error sensors between the controller output and the error signals in control systems,the error channel may cause the amplitude,phase and frequency change of the signals.In this paper,Fx LMS adaptive control algorithm based on the error channel off-line identification is used for simulation of the control system.Based on dSPACE hardware-in-the-loop simulation system,a self-adaptive active control system for singlefrequency and dual-frequency signals is built,and a significant control effect is achieved.
s:vibration and wave;FxLMS;off-line identification;dSPACE
TH113.1
:A
:10.3969/j.issn.1006-1355.2017.04.010
1006-1355(2017)04-0047-05
2017-01-16
国家自然科学基金资助项目(51579242);国家自然科学基金青年基金资助项目(50509203)
黄驰(1993-),男,湖北省汉川市人,研究生,主要研究方向为主动控制算法。
E-mail:1436163504@qq.com
