不同删失比例下AFT模型与Cox模型表现比较的模拟研究*

昆明医科大学公共卫生学院流行病与卫生统计学系（650500） 肖媛媛 陈 莹 何利平 喻 箴 许传志

不同删失比例下AFT模型与Cox模型表现比较的模拟研究*

昆明医科大学公共卫生学院流行病与卫生统计学系（650500） 肖媛媛 陈 莹 何利平 喻 箴 许传志△

目的 评价当生存数据出现不同删失比例的条件下，AFT模型和Cox模型的表现优劣。方法 采用自编SAS宏程序模拟不同参数设置、不同比例均匀删失的Weibull分布，分别采用AFT模型和Cox模型对模拟产生的数据进行拟合，并从偏倚、准确性和覆盖程度三个指标对两个模型的表现进行评价。结果 在分布参数和自变量效应值固定的情况下，AFT模型在参数估计偏倚和准确性两方面的表现却始终优于Cox模型。删失比例越大，AFT模型的表现相对而言越优异。而在覆盖程度方面，对于相同参数设置及删失比例的模拟数据，两个模型的表现相似。结论 AFT模型的总体表现优于Cox模型，当删失生存数据同时满足两类模型的应用条件时，应该优先选择偏倚更小、准确性更高的AFT模型进行分析。

AFT模型 Cox模型 删失比例 表现 模拟研究

作为最为常见的两类生存分析模型，Cox模型与AFT模型在不同条件下的表现比较是一个引人关注的问题，也有部分学者曾经探讨过，但大都集中在参数估计的准确度及数据拟合优度的比较方面。如Orbe等采用随机数据模拟的方法比较了一类半参数AFT模型和Cox模型的拟合优度，发现半参数AFT模型得到的结果更为准确［1］；Qi在运用AFT模型和Cox模型拟合同一真实数据后发现AFT模型的拟合优度要高于Cox模型［2］；Sayehmir等［3］，Ponnuraja等［4］，Nawumbeni等［5］将AFT模型和Cox模型同时运用于真实数据，发现AFT模型的预测表现明显优于Cox模型等。但目前尚无研究讨论在应用条件同时满足时，不同删失数据比例下AFT模型和Cox模型的表现比较。本研究拟采用随机数据模拟的方法对这一问题进行初步探讨。

对象与方法

1．选择模拟分布

要对AFT模型和Cox模型的表现进行对比，就必须采用同一模拟数据集。因此，模拟的数据集必须同时满足AFT模型和Cox模型的应用条件，即比例风险和恒定加速失效因子。常见的生存分布类型中，只有两种分布同时满足上述两个应用条件，指数分布（exponential distribution）和Weibull分布（Weibull distribution）。考虑到指数分布是Weibull分布的特例，为不失一般性，本研究选择Weibull分布为模拟分布。

2．模拟设计

（1）模拟条件设定

为了集中讨论不同参数条件下删失比例对两类模型表现的影响，在数据模拟前，我们对模拟数据的其他特征简化设定如下：只研究单一自变量，且为了兼顾统计效能，该自变量取值定义为满足参数为B（1，0．5）的二项分布；所有模拟组别均为大样本（N＝1000），不考虑样本含量对结果的影响；只考虑随机删失，且删失分布定义为均匀分布；考虑到Weibull分布中尺度参数λ的作用仅为拉伸或压缩原始分布，并不改变其形状，因此总可以用固定系数将其还原为原始分布，故模拟研究中不再考虑它的变化对结果的影响，所有模拟组均设置为1。

（2）产生生存时间

目前在随机模拟产生满足比例风险假定的生存时间分布，即指数分布、Weibull分布和Gompertz分布时，经常采用的是Bender等于2005年提出的模拟方法［6］。本次研究也采用上述方法随机产生生存数据，具体步骤为：①采用SAS统计分析软件产成［0，1］上均匀分布的随机变量U，样本含量为N；②根据预先设定的分布参数λ、γ以及协变量的回归系数向量β，结合生成的随机变量U的取值，利用公式1转换得到生存时间T，样本含量同样为N。

（3）生成含特定比例删失的生存数据

在进行生存数据的随机模拟研究时，删失数据的生成远比完整数据复杂得多，尤其是含特定比例删失的数据。除非特别说明，本文所指代的删失均为随机删失。在前期对相关领域文献进行细致检索和梳理后，我们发现：虽然有学者已经提出了一些含特定比例删失生存数据的模拟方法，但这些方法或是在逻辑架构上就存在欠妥之处，或是经实际验证无法得到设定删失比例的生存数据。正是由于现有研究存在上述不足，在当前研究中，我们采用自行编制的SAS宏程序随机模拟产生含特定比例删失的生存数据。该宏程序的编制思路、步骤及具体的程序步骤我们已在前期发表的一项研究中进行过详细描述［7］。

（4）模拟策略

前面已经述及，根据研究目的，模拟所需的部分非重点关注参数和特征已经设置为恒定。在设置模拟策略时，只重点关注Weibull分布形状参数γ，比例风险效应系数β和删失比例设定值P的变化对两类生存分析模型表现的影响。因此，最终确定执行如下4组模拟，其中，每组模拟均执行删失比例分别为10%、20%、30%、40%、50%、60%、70%、80%、90%的9小组模拟（表1）。

在进行模拟研究时，依据所要达到的估计值准确度的大小，可以采用公式（2）计算单次模拟的模拟次数［8］：

上式中，σ是所估计参数的标准差，δ是预先设定的参数估计精度，可用标准差的百分位数表示，Z1-（a／2）是标准正态分布下第1-（a／2）百分位数的取值，1-θ为检验效能。

本次研究中，δ取σ的15%，检验效能定为90%，由此计算得到的模拟次数为467次。为方便起见，每小组模拟重复次数统一取500次。

3．模型表现评价指标

随机数据模拟研究在评价特定模型拟合变现时，通常采用如下三个方面的指标：偏倚（bias）、准确性（accuracy）和覆盖程度（coverage）［8］。本次研究中将每次通过完整数据得到的参数估计值作为金标准，也从上述三个方面出发设定如下评价指标：

（1）偏倚：评价指标为采用删失数据得到的模型参数估计值＾β与使用完整数据拟合模型得到的参数估计值＾β0相比的相对绝对偏差，其计算公式参见公式（3）：

（2）准确性：评价指标为采用删失数据得到的模型参数估计值＾β的标准差＾S与使用完整数据拟合模型得到的参数估计值＾β0的标准差＾S0的比值，其计算公式参见公式（4）：

（3）覆盖程度：覆盖程度是指用模拟数据得到的效应估计值多大程度覆盖了真实效应值。本次模拟研究采用显著性一致率来评价覆盖程度，定义为使用完整数据得到的参数估计值＾β0显著（P＜0．05）的模拟次数（N）中，采用删失数据得到的参数估计值＾β也同样显著的次数（Nacco）所占的百分比。其计算公式参见公式（5）：

结 果

1．偏倚

（1）两模型总体比较

从图1可以看出，在四组模拟策略下，不论生存分布的形状参数γ及自变量X的效应系数β如何设置，随着删失比例的增加，Cox模型和AFT模型的偏倚都逐渐加大，但在任何删失比例下，AFT模型的偏倚均小于Cox模型的偏倚。

在四组模拟策略下，随着删失比例的增加，AFT模型和Cox模型的偏倚之差逐渐增大。删失比例在70%以下时，两模型偏倚之差增速较缓；当删失比例超过70%时，偏倚之差陡增。此外，在删失比例小于70%时，模拟数据参数设置对两类模型偏倚之差的影响不大，而当删失比例大于70%时，随着形状参数γ的增大，或效应系数β的减小，AFT模型和Cox模型的偏倚之差迅速增大（图2）。

（2）不同形状参数下两类模型的偏倚变化

从图3可以看出：对两类模型而言，当删失数据比例小于60%时，形状参数γ的变化对偏倚的影响不大；而当删失比例大于60%时，随着删失比例的增加，γ对偏倚的影响逐渐增大。尤其是Cox模型，大约在缺失比例50%时，γ对偏倚的影响开始显现，到缺失比例90%时，γ＝2时的偏倚比γ＝0．5时的偏倚大约9%（35．2%和26．2%）。对AFT模型而言，偏倚的增幅不明显，同样在缺失比例90%时，γ＝0．5和γ＝2的偏倚差距仅为不到2%（13．0%和11．2%）。

（3）自变量不同效应参数下两类模型的偏倚变化

从图4可以看出：在任一删失比例下，当研究因素X的效应逐渐减弱时，Cox模型和AFT模型的偏倚均逐渐增大。偏倚的增加速度也随删失比例的增大而增大，尤其当删失比例大于70%时，效应参数越小的组别偏倚的增大越快。如删失比例从70%上升至90%、γ＝2、β＝0．2时，Cox模型偏倚的增加达到了1．1倍（43．3%到91．9%），虽然AFT模型在偏倚绝对值方面的表现明显优于Cox模型，但其偏倚增速却与Cox模型接近，为0．9倍（34．2%到65．7%）。

图1 不同参数及删失比例下Cox模型和AFT模型偏倚

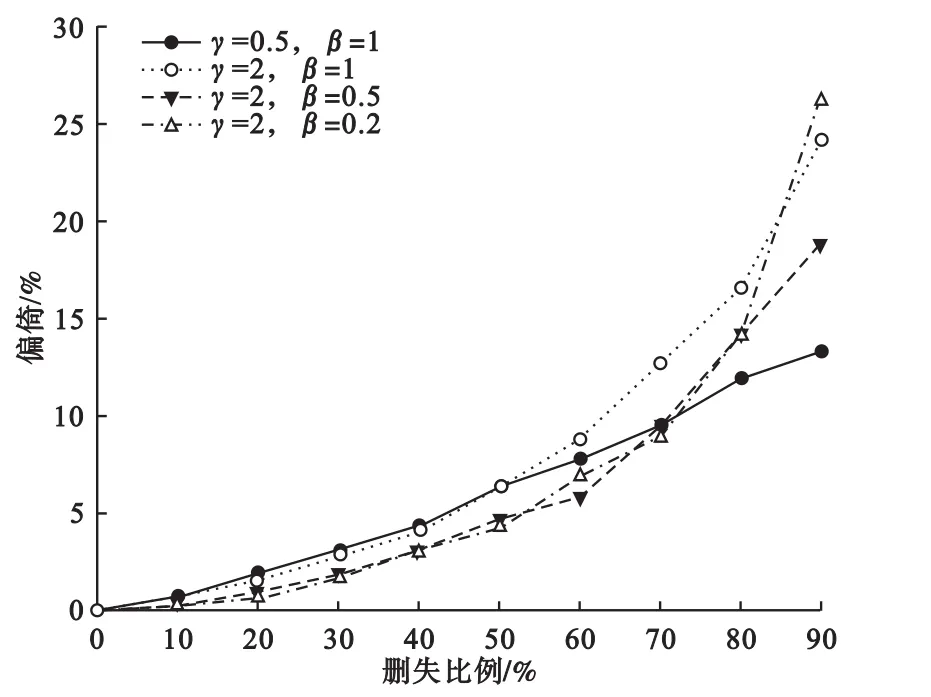
图2 不同参数及删失比例下Cox模型和AFT模型偏倚之差

2．准确性

对于Cox模型和AFT模型，随着删失比例的增加，其参数估计的标准差与通过完整数据得到的标准差之间的比值逐渐增大，意即其参数估计的准确性逐渐降低。尤其是在删失比例大于70%后，准确性加速降低。生存时间形状参数γ和自变量X效应系数β的变化对两类模型参数估计的准确性无明显影响：以四组模拟中删失比例30%为例，Cox模型得到的准确性估计值皆为1．2，AFT模型得到的准确性估计值皆为1．14；再如删失比例70%时，Cox模型得到的准确性估计值依次为1．85、1．84、1．83、1．83，AFT得到的准确性估计值依次为1．63、1．56、1．57、1．56。

在四组模拟数据中，在任一删失比例下，AFT模型参数估计的准确性表现始终优于Cox模型，且差距随删失比例的增大而增大。当四组模拟数据删失比例达到90%时，采用Cox模型计算得到的参数标准差是完整数据参数标准差的约3．2倍，而AFT模型介于2．4～2．7倍（图5）。

3．覆盖程度

不同删失比例下Cox模型和AFT模型得到的显著性一致率如表2所示。不难看出，在自变量X的效应较强时（β＝1），删失比例的变化对两种模型的显著性一致率无影响，均为100%。而当自变量的效应逐渐减弱时，随着删失比例的增加，两种模型在显著性一致率方面的表现逐渐下滑，且下滑速度相当。如当β＝0．2，γ＝2时（组号＝4），对应Cox模型中X所导致的风险比为1．2，AFT模型中X加速失效因子为0．9，删失数据比例为50%及以下时，两种模型的显著性一致率均大致高于80%。当删失比例高于50%时，显著性一致率加速下滑，特别当删失比例达到90%时，两种模型的显著性一致率均仅为30%左右。

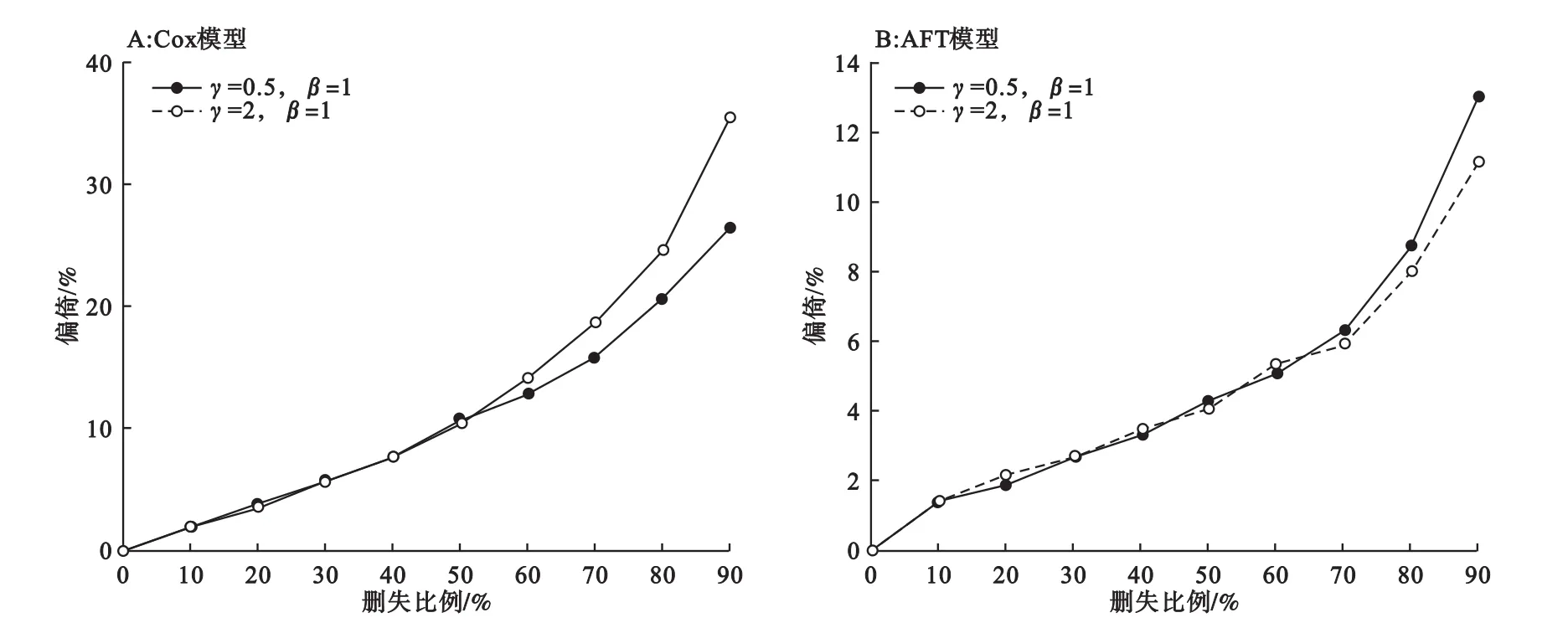
图3 形状参数γ不同时Cox模型和AFT模型偏倚随删失比例变化趋势

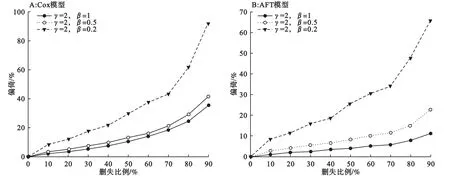
图4 自变量X效应系数β不同时Cox模型和AFT模型偏倚随删失比例变化趋势

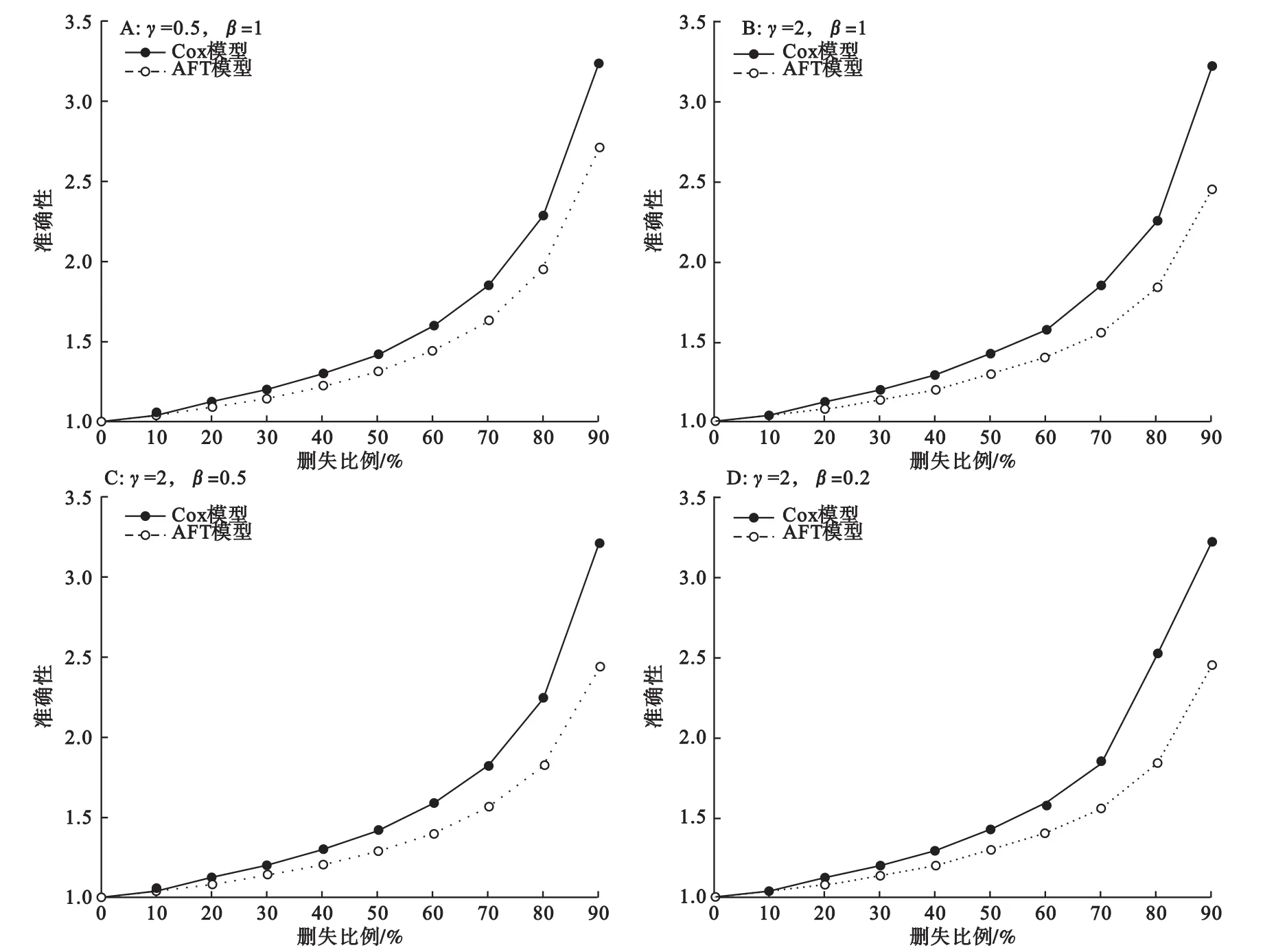
图5 不同参数及删失比例下Cox模型和AFT模型准确性

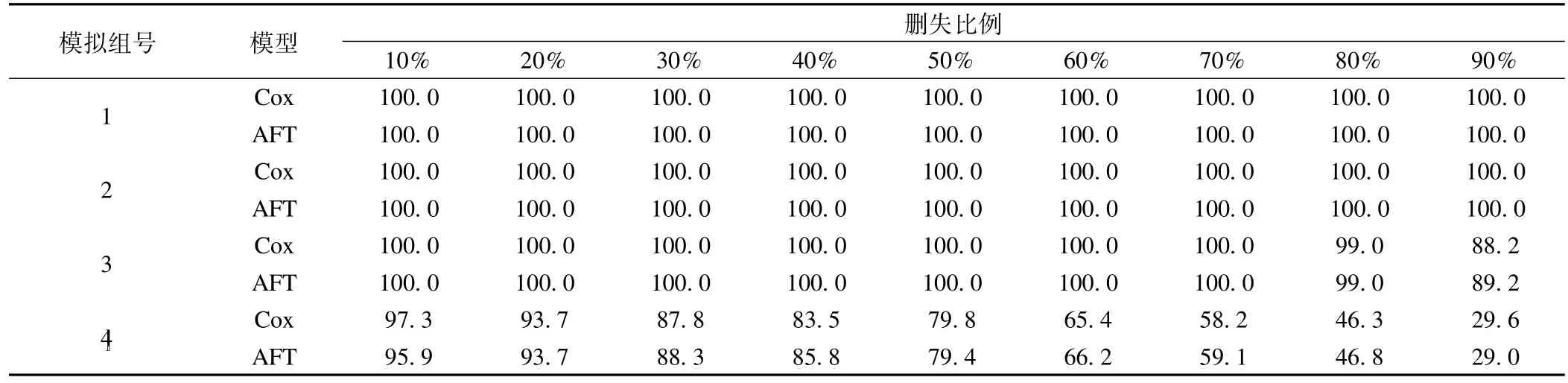
表2 不同参数及删失比例下Cox模型和AFT模型显著性一致率（%）

讨 论

本研究以Weibull分布为模拟分布，讨论了在分布参数和自变量效应值取值不同的情况下，生存时间删失比例对Cox模型和AFT模型表现的影响。研究发现：在分布参数和自变量效应值固定的情况下，随着生存时间删失比例的增加，Cox模型和AFT模型在参数估计方面的偏倚均增大，准确性均降低，尤其是在删失比例大于70%时，两类模型在偏倚和准确性方面的表现更是加速下滑。其中，删失比例对Cox模型表现的影响与前文提到的一项研究结果一致［8］，而生存数据删失比例对AFT模型表现的影响则尚未查见既往文献报道。

尽管随着删失比例的增加，两类模型在偏倚和准确性方面的变化趋势一致。但对于特定删失比例的生存数据，在分布参数和自变量效应值固定的情况下，AFT模型在参数估计偏倚和准确性两方面的表现却始终优于Cox模型。删失比例越大，AFT模型的表现相对而言越优异。以偏倚方面的表现为例，当生存分布的形状参数γ＝2，自变量X的效应参数β＝1时，删失比例为40%时，Cox模型的偏倚约为AFT模型的2倍，而当删失比例增加至90%时，Cox模型的偏倚约为AFT模型的3倍。再从准确性方面来看，同样的形状参数和自变量效应参数情况下，删失比例为40%时，Cox模型的参数标准差为金标准的1．3倍，AFT模型的参数标准差为金标准的1．2倍，当删失比例增加至90%时，Cox模型的参数标准差增至金标准的3．2倍，而AFT模型的参数标准差却只增至金标准的2．5倍。

在医学研究中，生存分析一般都运用于纵向研究所获取的数据。受限于研究的成本投入及伦理学标准，纵向研究的时间往往比较有限。正是因为如此，医学领域所涉及的生存分析一般会包含较大比例的删失数据。在Web of Science中随机搜寻新近发表的肿瘤生存分析文献就不难发现这一现象。如Heemskerk-Gerritsen等发表的一项关于乳腺癌的生存分析研究有88%的删失［9］，再如Cardwell等发表的另一项关于乳腺癌生存分析的研究中，删失数据占92%［10］。考虑到医学研究中生存数据的特点和本次模拟研究所得到的结果，当生存数据同时满足Cox模型和AFT模型的应用条件时，应该优先选择偏倚更小、准确性更高的AFT模型进行参数估计。

当研究因素真实效应较弱时，如果生存时间删失比例同时过高，则不论AFT模型还是Cox模型，其正确判断真实效应显著性的能力均受到较大影响。本次模拟中，研究因素HR＝1．2，即加速失效因子＝0．9时，若删失比例为80%以上，则正确判断的比例低于50%。因此在运用AFT模型或Cox模型进行生存分析时，一旦预判某一研究因素的真实效应较弱，同时生存时间删失比例较大时，对分析结果的解读需谨慎。

［1］Orbe J，Ferreira E，Núñez-Antón V．Comparing proportional hazards and accelerated failure timemodels for survival analysis．Statistics in Medicine，2002，21（22）：3493-3510．

［2］Qi J．Comparison of proportional hazards and accelerated failure time models［D］．University of Saskatchewan，2009．

［3］Sayehm iri K，Eshraghian MR，Mohammad K，et al．Prognostic factors of survival time after hematopoietic stem cell transplant in acute lymphoblastic leukem ia patients in Shariati hospital，Tehran．Journal of Experimental＆Clinical Cancer Research，2008，27：74．

［4］Ponnuraja C，Venkatesan P．Survivalmodels for exploring tuberculosis clinical trial data-an empirical comparison．Indian Journal of Science and Technology，2010，3（7）：755-758．

［5］Nawumbeni DN，Luguterah A，Adampah T．Performance of Cox proportional hazard and accelerated failure timemodels in the analysis of HIV／TB co-infection survival data．Research on Humanities and Social Sciences，2014，4（21）：94-102．

［6］Bender R，Augustin T，Blettner M．Generating survival times to simulate Cox proportional hazardsmodels．Statistics in Medicine，2005，24（11）：1713-1723．

［7］肖媛媛，许传志，赵耐青．含特定比例均匀随机删失生存数据的SAS模拟实现．中国卫生统计，2016，33（6）：1058-1059．

［8］钱俊．生存分析中删失数据比例对Cox回归模型影响的研究．南方医科大学，2009．

［9］Heemskerk-Gerritsen BA，Rookus MA，Aalfs CM，et al．Improved overall survival after contralateral risk-reducingmastectomy in brca1／2 mutation carriersw ith a history of unilateral breast cancer：a prospective analysis．International Journal of Cancer，2015，136（3）：668-677．

［10］Cardwell CR，Hicks BM，Hughes C，et al．Statin use after diagnosis of breast cancer and survival：a population-based cohort study．Epidemiology，2015，26（1）：68-78．

（责任编辑：邓 妍）

国家自然科学基金（81460519）；云南省自然科学基金（2013FZ064）

△通信作者：许传志，E-mail：xuchzhi＠qq．com