基于LASSO类方法的Ⅰ类错误的控制*

山西医科大学卫生统计教研室（030001） 许树红 王 慧 孙红卫 王 彤

基于LASSO类方法的Ⅰ类错误的控制*

山西医科大学卫生统计教研室（030001） 许树红 王 慧 孙红卫 王 彤△

全基因组关联研究（genome-w ide association studies，GWAS）是在全基因组范围内同时研究上百万个单核苷酸多态性（single nucleotide polymorphism，SNP）位点与疾病或某些性状之间的关联，从而筛选出可能的致病SNP位点，进而对这些位点进行人群验证和实验分析。在GWAS研究中比较传统的分析方法是针对每个SNP和结局变量间关联进行单因素分析的假设检验，而待分析的SNP数量有几十万甚至上百万个，使得检验次数十分巨大，如果不采用合适的方法进行多重性校正来妥善控制Ⅰ类错误，会产生许多假阳性结果，对这些结果进行验证将耗费很多时间和财力，造成不必要的损失。针对全基因组测序数据进行多因素建模常采用的分析策略为降维和变量选择。变量选择的方法包括经典方法和惩罚类方法，惩罚类方法在GWAS研究、测序数据分析中应用广泛且发展迅速，它假定模型具有稀疏性即真实情况下许多未知候选变量的回归系数为0或者接近0，因此自变量的选择问题转化为确定正确的子模型问题，且在选择变量的同时给出模型参数的估计。LASSO（least absolute shrinkage and selection operator）作为一种常用的惩罚类方法，部分研究者指出其选出的变量存在较高的假阳性问题［1-3］。针对该类问题，在多重校正以及变量选择方法的基础上，发展了一些控制Ⅰ类错误的同时筛选出正确变量的方法。本文主要对多重检验中控制Ⅰ类错误的方法进行总结并且对基于LASSO的Ⅰ类错误的控制方法进行综述。

多重检验中控制Ⅰ类错误的策略和方法

经典的多重检验校正是建立在多个检验之间或P值之间相互独立的假设上［4］，然而在针对基因数据的多个假设检验中得到的P值之间往往是不独立的，目前处理这种不独立情况的方法大致分为三类：第一种是不做任何假设；第二种是假设P值之间存在PDS假设（positive dependence through stochastic ordering，PDS）［5-7］，PDS假设有弱PDS假设和强PDS假设两种，前者为：对每一个成立的H0对应的P值qi，及所有qi的不减函数f，在qi＝u的条件下，E [f（q1，…，qm0）｜qi＝u]是不减的，后者为：对每一个H0对应的P值pi及其不减函数f，在qi＝u的条件下，E [f（p1，…，pm）｜qi＝u]是不减的；第三种是基于排列抽样的方法。目前常用的控制Ⅰ类错误的方法有两大类，分别是控制FWER（family-w ise error rate，FWER）和控制FDR（false discovery rate，FDR）。

设进行m次假设检验，原假设为H0，i，i＝1，…，m，对应的P值表示为pi，i＝1，…，m。将成立的H0对应的P值定义为qi，i＝1，…，m0。表1是各种可能的检验结果，m0和m1分别是检验中成立的H0及不成立的H0的个数。V是检验中成立的H0被错误拒绝的个数。π0＝m0／m，是m次假设检验中成立的H0所占比例。

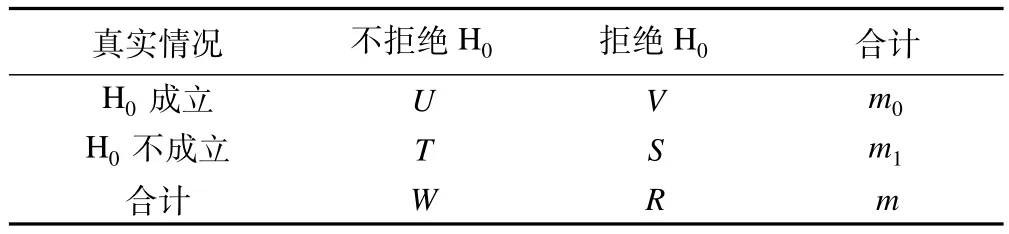
表1 多重检验的结果

1．控制FWER

FWER定义为至少犯一次Ⅰ类错误的概率，FWER＝P（V≥1），是传统的多重检验中广泛应用的控制Ⅰ类错误的指标。控制FWER的方法有经典的Bonferroni方法，当pi＜α／m时，拒绝相应的假设，公式1证明了Bonferroni方法可将FWER控制在π0α水平。

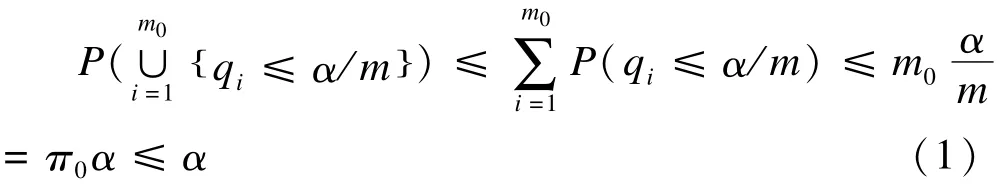
由此，当真实的H0全部成立时控制FWER是弱控制，此时FWER被控制在α水平；当真实的H0部分成立时控制FWER是强控制，且若不成立的H0的个数很多，FWER将被控制在远低于α的水平，此时Bonferroni方法便会很保守［7］。因此Holm在1979年提出Holm方法［8］，在Bonferroni方法基础上，迭代进行检验，第一步拒绝pi＜α／h0的假设，h0＝m；第二步排除掉第一步已经拒绝的假设，剩余没有被拒绝的假设数为h1，拒绝pi＜α／h1的假设；以此类推，直到没有假设被拒绝为止。Holm证明该方法能将FWER控制在α水平。Holm方法的另一种解法是首先将P值从小到大进行排序即p（1）≤p（2）≤…≤p（m），将p（i）与α／(m-i+1)进行比较，得到最小的j满足p（j）＞α／(m-j+1)，然后拒绝所有j-1假设。Bonferroni和Holm方法都没有对P值之间的关系做假设，即对P值的联合分布没有假设。Hochberg［9］利用成立的H0满足弱PDS假设，在Holm方法基础上进行了修改，Hochberg方法是首先将P值从小到大进行排序即p（1）≤p（2）≤…≤p（m），将p（i）与α／(m-i+1)进行比较，得到最大的j满足p（j）＜α／(m-j+1)，然后依次拒绝所有j假设。Westfall＆Young［10］利用排列抽样方法来控制FWER，其原理是在H0假设成立条件下，样本来自相同的总体，可以对原始样本进行重新抽样，得到统计量的分布并进行检验。排列抽样方法应用很广，不仅可以用来控制FWER，也可以控制FDR等。Westfall＆Young的方法虽然在P值之间不独立时效能比前面提到的方法高，但是排列抽样对原假设间的一致性有要求。

随着基因工程和下一代测序技术的迅猛发展，产生庞大的生物信息数据，通过在多重检验中控制FWER来控制Ⅰ类错误，对于探索性研究而言结果太过保守，FWER将每个假设检验的可信度控制在1-α水平，这只能识别出少数有意义的基因或者变量，且在严格控制Ⅰ类错误的同时其Ⅱ类错误偏大。它的优势在于对每一个假设都严格控制Ⅰ类错误，在其选出的基因集中任意子集都对Ⅰ类错误有很好的控制，适用于对每个假设均有要求的验证性研究。

2．控制FDR

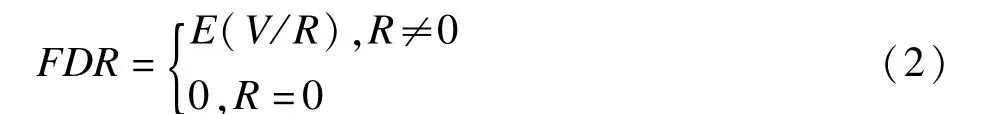
FDR与FWER之间的关系为：当m0＝m时，即全部原假设均成立，此时FDR的控制与FWER的控制等价；当m0＜m时，FDR小于或者等于FWER，因此，FDR相当于弱控制FWER［11-12］。

B-H方法可简单表述为：先将P值从小到大进行排序即p（1）≤p（2）≤…≤p（m），然后将p（i）与iα／m进行比较，将FDR控制在α水平，定义j＝max {i：p（i）≤iα／m}，然后拒绝所有j假设，若没有满足条件的i存在，则没有假设被拒绝。Benjamini＆Hochberg已证明当P值间相互独立的时候，B-H方法能将FDR控制在π0α水平而不是α水平，故其结果有些保守。大量文献在B-H的方法基础上进行了改进，如将iα／m换为iα／（π＾0m），其中π＾0是π0的估计值，并针对π0的估计提出很多方法，该类方法为“自适应”方法［13-14］。原始的B-H方法要求P值间相互独立，而当P值间不独立时，许多研究者提出了相应的改进方法以及一些基于重抽样的方法，如Yekutieli提出了ssBH方法［15］，Benjam ini＆Yekutieli提出基于排列抽样的方法但是没有完全证明该方法能控制FDR［16］，Joseph［17］等以及Troendle［18］提出了基于bootstrap的方法也能渐近控制FDR，但bootstrap的方法要求真实H0对应的P值的联合分布的极限满足可交换性［19］。除了控制FDR，还有一类方法是对选出的结果集的FDP（false discovery proportion）进行估计。FDR控制与FDP的估计是有区别的。例如：某个研究者重复一个实验z次，采用控制FDR的方法进行分析，那么可能得到z个不同的结果集Ri，i＝1，…，z，每一个结果集都有其未知的FDP，记为Qi。当Z很大时，Qi的期望将接近FDR的控制水平。Q＾i为第i个结果集的FDP的估计值［7］。FDP的估计方法大多是从贝叶斯角度解释，几个代表性的方法是Storey 2003年提出的q-value法、Tusher 2001年提出的SAM（significance analysis ofm icroarray）方法、Efron 2001年提出的基于经验贝叶斯的方法等，2012年刘晋等对这类方法进行了比较详细的介绍［12］。在P值间不独立的情况下，Fan等［20-21］在Storey［22］和Friguet［23］基础上，提出PFA（principal factor approximation）法，该方法在进行多重检验校正时，通过因子分析将变量间相关关系考虑在内，提出适用于任意不独立情况的FDP的近似公式和一致估计。除此之外，一些文献对FDP的置信区间进行了估计［24-25］，如Meinshausen基于排列抽样的方法。

目前在基因数据分析领域的多重比较问题中，FDR已经成为一个标准有效的反映Ⅰ类错误的指标，适用于探索性研究，在整体上控制Ⅰ类错误的同时能筛选出更多有意义的基因。然而FDR也存在一定的局限性，其一是FDR是随机变量Q的期望值，当P值间不独立时或者一些FDR估计方法的假设不满足时，分析结果中Q＾的变异可能会增大［7，12］；其二是控制FDR的条件下得到的分析结果是从整体上控制了Ⅰ类错误，无法保证控制了每个假设或者每个结果的子集的Ⅰ类错误。因此研究者在解释其结果时需要注意保持结果集的完整性［7］。

基于LASSO类方法的控制Ⅰ类错误的策略和技术

随着生物信息技术的快速发展、大数据时代的到来，高维数据分析问题不断涌现（本文中高维数据是指p＞n的情况，p和n分别表示自变量个数和样本量），面对复杂数据建模时如何更加准确的筛选变量成为很重要的问题。随着计算能力的提高和算法的不断改进，惩罚类方法因其通过好的算法能执行较大维度的变量选择过程、得到稀疏解而逐渐受到重视，是目前比较流行的变量选择方法。该类方法假定模型具有稀疏性，即真实模型中很多自变量的回归系数为0，其思想是在最小化损失函数或者最大化似然函数的同时增加一个惩罚项来筛选变量并估计其回归系数，将回归系数不为零的变量直接选入结果集中。常见的惩罚类方法有：LASSO、SCAD（smoothly clipped absolute deviation）、弹性网（elastic net）、MCP（minimax concave penalty）等。

1．LASSO中关于调整参数选择的传统方法

基于LASSO的变量选择及回归系数的估计，在很大程度上受调整参数λ的影响，因为调整参数值的大小影响着模型的复杂程度及模型的收敛速度，因此选择合适的调整参数十分重要［26-27］。传统的选择调整参数的方法大致分为两类：交叉验证（cross validation，CV）和信息准则（information criteria）。

（1）交叉验证

最常用的交叉验证是K折交叉验证（K-fold cross-validation），K为整数，1＜K≤n。该方法的过程是：首先将原始样本Γ拆分成K个相同大小的子样本，将其中一个子样本选为验证数据集Γv，其余K-1个子样本为训练数据集Γ-Γv，利用训练数据集来建立模型，然后用拟合模型来预测验证数据集，计算验证集的预测值与真实值间的偏差，重复以上过程K次，计算平均偏差，选择平均偏差最小时对应的调整参数值。

基于最小二乘的K折交叉验证的目标函数为［28］：

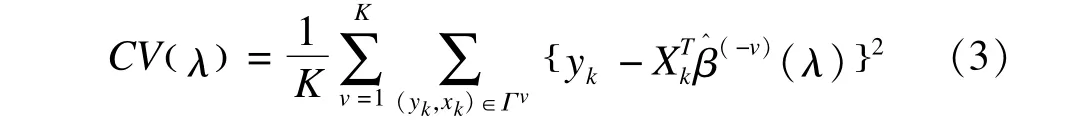
其中，β＾（-v）（λ）表示去掉（yk，xk）∈Γv后的回归系数估计值，使CV（λ）取得最小值时对应的λ为最终模型的调整参数。

基于对数似然函数的K折交叉验证的目标函数为［27］：

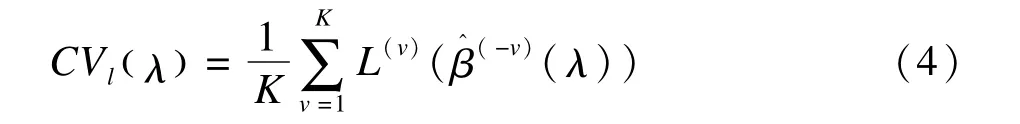
其中，β＾（-v）（λ）表示去掉第v份数据后的回归系数估计值，L（v）（β＾（-v）（λ））表示第v份数据为验证集时求得的对数似然函数值，使CVl（λ）取得最大值时对应的λ为最终模型的调整参数。

当K＝n时的交叉验证称为留一法（leave-oneout），该方法是对真实的预测误差的渐近无偏估计，但是该法方差很大且计算量庞大［26］。Tibshirani1996年使用广义交叉验证（generalized cross validation，GCV）选择调整参数，GCV在CV的基础上将有效参数的个数考虑在内估计预测误差。

（2）信息准则

信息准则一般包括模型拟合程度的测量（如似然函数或损失函数）以及对模型复杂程度的惩罚（惩罚乘子an）两部分［29］。对于一个给定的统计模型如线性模型、生存模型，不同的信息准则方法的主要区别在于如何对模型的复杂程度进行惩罚，然而，对于选择真实的模型而言，如何通过对模型复杂程度进行合理的惩罚来优化信息准则十分关键［30］。常用的信息准则有：AIC（Akaike information criterion）、BIC（Bayesian information criterion）、RIC（Risk inflation criterion）［31-33］等。an＝2和an＝log（n）分别对应的是AIC和BIC，an＝2log（p）为RIC，其中n为样本量，p为非零回归系数的个数。Yang和Wang指出CV以及GCV类似于传统的AIC，三种方法在高维数据情形下均易出现过拟合，且AIC不是一致的信息准则［34-36］。Wang［36］的研究表明针对SCAD，BIC能一致的选择真实的模型，但是随着样本量增大，BIC得到的结果可能会太保守，易遗漏一些重要的变量［37］。

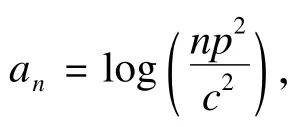
2．线性模型中基于LASSO类方法的控制Ⅰ类错误的方法

假设有n个样本，y表示研究的反应变量，X为n ×p维的自变量矩阵，β是回归系数，z是随机误差，z～N 0，σ2

()I。线性模型为：

基于LASSO的目标函数为：

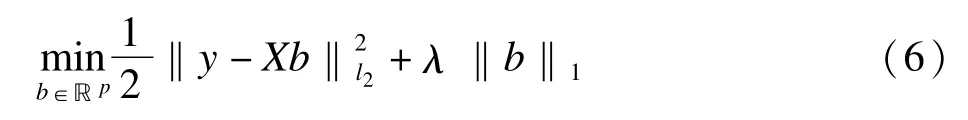
其中b是β的估计值，λ是调整参数。

（1）平稳选择（stability selection）

平稳选择法是将变量选择算法和再抽样技术相结合的方法，由Meinshausen和Bühlmann［42］提出，通过计算机对样本进行随机无放回抽样得到样本量为n／2的子样本I，然后利用LASSO等惩罚回归方法进行变量选择，选入模型的变量估计为β＾λj()I，选入模型的变量集为：

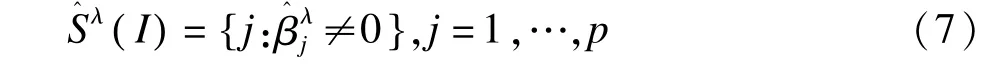
对不同的λ，每个变量j被选入模型的概率为：

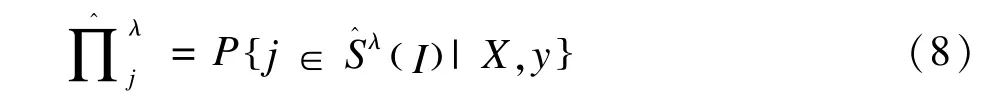
平稳选择法将其中被选取概率大于阈值的变量选入最终模型，最终变量集为：

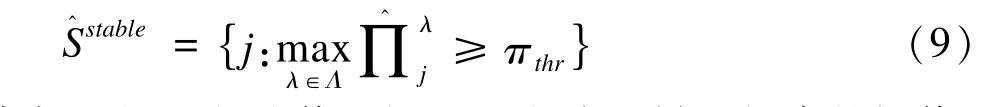
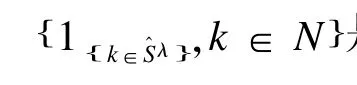
平稳选择法在R软件中可以实现。一般随机抽取子样本数达到500到1000即可，其计算成本较交叉验证相差不多甚至更低［43-45］。该方法不单独使用，而是与其他变量选择方法结合使用，应用于不同模型中。该法通过再抽样技术降低了模型结果对调整参数选择的敏感性，并达到了控制Ⅰ类错误的目的。但是由于基因之间往往存在一定的关联，其选择变量集可交换的假设不一定成立，且有文献报道在真实有意义的变量数极少的情况下，该方法的FDR值有时会很高，失去其控制Ⅰ类错误的作用［37］。

（2）SLOPE

SLOPE（sorted L-one penalized estimation）方法［3，46-48］，该法是在LASSO的基础上结合控制FDR的B-H方法提出的。其模型是：

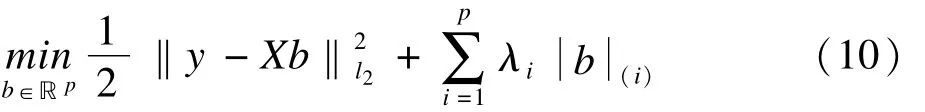
其中λi表示第i个变量的调整参数值，b（i）表示第i个变量的回归系数绝对值，λi满足λ1≥λ2≥…≥λp≥0降序排列，且λi的顺序根据λBH（i）来决定，相应的

SLOPE方法首先在X是正交矩阵的条件下（XTX＝Ip），根据线性模型公式5构造y～，模型为：

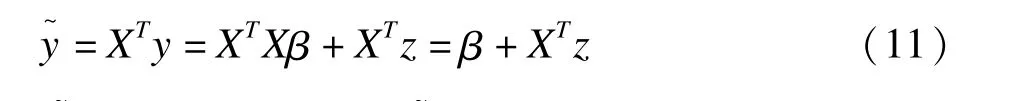
其中y～∈N(β，σ2Ip)，当时拒绝原假设。其次，在处理高维数据的LASSO方法基础上进行改进，不同效应的变量对应的调整参数值不同，令λBH（i）＝z（1-i·α／2p），其中z(α)为标准正态分布的分位数，λi＝λBH（i）·σ，根据λi来选择估计变量。Bogdan等证明在X满足正交矩阵的条件下SLOPE方法能将FDR控制在α水平内。

当X不满足正交矩阵的条件时，Bogdan等对λBH（i）进行了调整，在计算某一变量的λBH（i）时将其他变量的影响考虑在内，提出λG(i)：

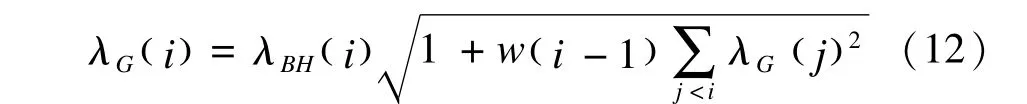
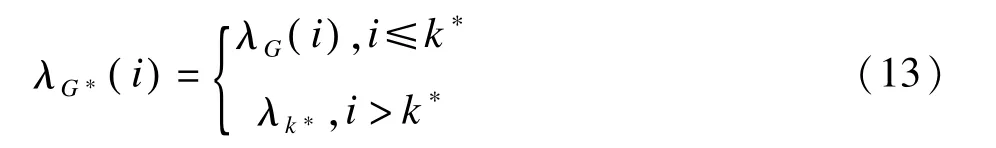
其中k*＝k( n，p，q)为最小的λG(i)的位置，λk*为λG(i)的最小值。

SLOPE借鉴多重检验校正中B-H方法的思想（B-H方法对P值从小到大排序，越小的p（i）其对应的检验水准iα／m值越小即检验水准越严格）改进LASSO，对不同效应的变量检验水准不同，效应越大的变量相应的检验水准越严格，其目的是为了控制FDR。SLOPE与LASSO的共同点在于两者对β＾i的估计均为有偏估计，不同点在于LASSO法只选择一个合理的λ值，根据估计β，Zi不为0，不同变量受到相同的惩罚。SLOPE根据λi来选择估计变量，不同的变量受到的惩罚不同，值越大的变量λi越大。鉴于SLOPE是有偏估计的方法，Bogdan等在其文章中并不推荐利用SLOPE对进行直接估计，而是建议使用两阶段法，第一阶段采用SLOPE法筛选出有意义的变量，第二阶段对筛选出的变量利用普通最小二乘法估计其回归系数。SLOPE方法在R、Matlab软件中可以实现。

（3）Knockoffs filter

Barber和Candès［49］提出一种新的在有限样本情况下筛选变量的方法，对任何自变量矩阵X∈Rn×p，n≥p，构造相应的knockoff变量矩阵X～，并将其与原始变量一同放入线性模型中，通过构建关于原始变量Xj与knockoff变量X～j的统计量Wj、确定统计量的界值T来控制线性模型中的FDR。

Knockoffs filter方法的过程分为三部分：

①对每一个原始变量Xj，j＝1，…，p构造knockoff变量X～j，要求knockoff保持原始变量之间的相关结构，即满足XTX＝X～TX～＝∑，XTjX～k＝XTjXk，j≠k，且假设∑矩阵可逆，同时要求knockoff变量X～j与原始变量Xj间相似程度尽可能地低，即对于XTX～＝∑－diag()s尽量选择大的s值。

②每对原始变量Xj和knockoff变量X～j构建一个统计量Wj。Barber和Candès在2014年的文章中给出很多种构建统计量Wj的方式，本文只详述其中之一说明Wj的意义。在LASSO公式（6）基础上，将自变量矩阵X换为增广矩阵X X[]～，定义Zj为原始变量Xj首次进入模型时的λ值，Zj＝supλ：β＾j()λ≠{

}0，相应的Z～j为变量X～j首次进入模型时的λ值，对于每对原始变量Xj和knockoff变量X～j，构建统计量Wj：

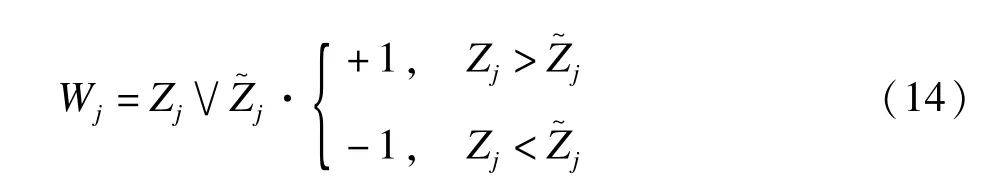
当Zj＝Z～j时，Wj＝0，若Wj为正并且值越大，说明原始变量Xj比knockoff变量X～j越早进入模型，则越有理由拒绝原假设。

③定义统计量的界值T，将满足Wj≥T的自变量选入模型。设FDR控制水平为q，在原假设βj＝0成立情况下，原始变量Xj与knockoff变量X～j两者谁先进入模型是随机性的，即Wj的正负号是随机的，那么对于任意的t，＃｛j：βj＝0 and Wj≥t｝＝d＃｛j：βj＝0 and Wj≤－t｝，其中＝d代表同分布。因此在t时，FDP的knockoff估计值为：

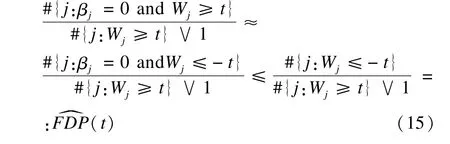
根据FDP的knockoff估计值定义T，T＝m in｛t∈W：FDP＾（t）≤q｝，最终界值T为：

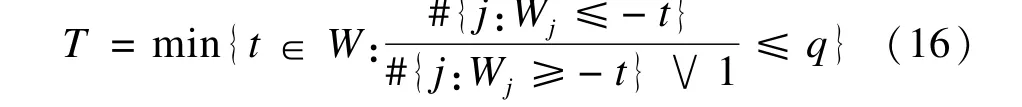
Knockoffs filter方法的关键之一在于knockoff变量的构造，当样本量n≥p时，Barber和Candès描述了如何构造X～以及如何选择合适的s值，但是当样本量n＜p时，∑矩阵可逆的假设不再满足，该方法不能直接使用，Barber和Candès［49］建议可以先使用一些降维的方法，再使用Knockoffs filter方法。Reid和Tibshirani［50］首先使用聚类处理自变量间相关的问题实现降维，然后用每个类别中选出的代表性的变量建模通过Knockoffs filter方法控制FDR。Barber和Candès［51］新提出一种分析策略应用于样本量n＜p的情况，该策略将观测分成两组，第一组观测的数据用于筛选潜在的有意义的自变量，其次在筛选出的变量基础上用第二组观测的数据，通过Knockoffs filter方法进行统计推断。目前Knockoffs filter方法可以通过R软件实现。

3．Cox模型中基于LASSO的控制FDR的方法

基于Cox模型的LASSO，其最大化目标函数为：

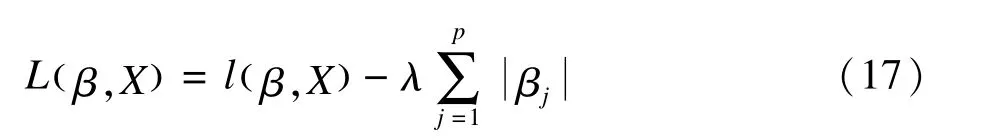
其中lβ，()X是Cox模型的对数似然函数，p为自变量个数。LASSO作为生存分析领域中常用的处理高维数据的方法之一，筛选的变量结果中存在FDR过高的问题，而调整参数的选择很大程度上影响了LASSO的变量选择和回归系数的估计。Ternès，Rotolo和M ichiels［37］针对传统的交叉验证法容易出现过拟合的问题，提出了一种改进的调整参数的选择方法，即pcvl（penalized cross-validated log-likelihood，pcvl），该方法主要在传统交叉验证的目标函数中加入惩罚项，以实现模型在满足拟合优度与模型稀疏程度两者之间的折中。

Ternès，Rotolo和M ichiels文章中传统K折交叉验证的目标函数是：

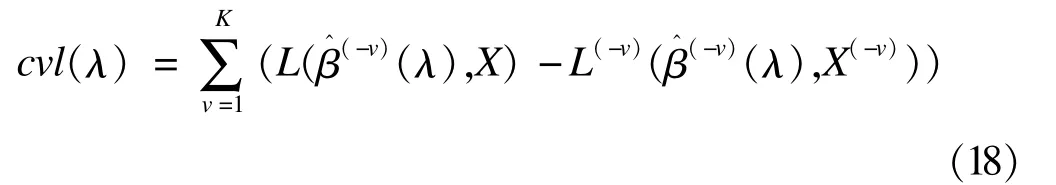
其中β＾（－v）（λ）表示去掉第v份数据后的回归系数估计值，L（β＾（－v）（λ），X）表示全部数据求得的对数似然函数值，L（－v）（β＾（－v）（λ），X（－v））表示去掉第v份数据时求得的对数似然函数值，使cvl（λ）取得最大值时对应的λ为模型的调整参数，记为λ＾cvl。该函数参考Verweij和van Houwelingen［52］文章中对生存分析中交叉验证法的介绍，与公式（4）的差别在于后者是利用全部数据的对数似然函数值与去掉第v份数据时求得的对数似然函数值之差来求第v份数据的对数似然函数，而且并没有取平均值。

令λ0表示没有变量进入模型时λ的最小值，即λ0＝minλ｜p{}＝0，惩罚项为：

Ternès，Rotolo和M ichiels将pcvl方法与传统CV法、AIC、RIC、自适应LASSO和平稳选择法进行了比较，模拟数据结果显示pcvl方法的优势在于控制FDR的情况下也能将假阴性率控制在较低水平。但是该方法是从适当增加λ值以减少LASSO筛选出的变量数的角度控制FDR，无法在建模时给定FDR的理想水平实现精确的FDR的控制。

表2 基于LASSO类方法的控制Ⅰ类错误方法的比较

展 望

本文首先回顾了多重假设检验中Ⅰ类错误控制方法，根据Ⅰ类错误控制指标的不同分为两大类：控制FWER的方法和控制FDR的方法，然而基因间不独立的问题对多重检验结果产生了一定的影响，同时在多变量情况下如何处理高维数据的问题也亟待解决，因此一些变量选择方法如惩罚类方法成为如今研究的热点。本文针对LASSO这一变量选择方法存在的FDR过高的问题，介绍了四种方法，分别为平稳选择法、SLOPE、Knockoffs filter和pcvl方法，已有一些研究分别将平稳选择法、SLOPE和pcvl方法与传统的调整参数选择方法进行了比较且结果显示平稳选择法、SLOPE和pcvl方法可以有效控制Ⅰ类错误，但这些方法各有优劣及适用条件，并非在任何数据情况下都有效，因此在应用这些方法时需注意适用条件是否满足。其中一些方法如平稳选择、Knockoffs filter等也可以扩展到其他惩罚回归模型中。LASSO惩罚估计是有偏的，不满足oracle的三个性质，未来如何将这些控制Ⅰ类错误的方法应用于其他惩罚类方法如SCAD、MCP等还需要进一步研究。

［1］Benner A，Zucknick M，Hielscher T，et al．High-dimensional Cox models：the choice of penalty as part of themodel building process．Biometrical Journal，2010，52（1）：50-69．

［2］Shojaie A，M ichailidis G．Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs．Biometrika，2010，97（3）：519-538．

［3］Bogdan M，Berg EVD，Su W，et al．Statistical estimation and testing via the sorted L1 norm．arXiv：1310．1969，2013．

［4］王彤，易东．临床试验中多重性问题的统计学考虑．中国卫生统计，2012，29（3）：445-450．

［5］Block HW，Savits TH，Shaked M．A concept of negative dependence using stochastic ordering．Statistics＆Probability Letters，1985，3（2）：81-86．

［6］Sarkar SK，Guo W．On a generalized false discovery rate．Mathematics，2009，37（3）：1545-1565．

［7］Goeman JJ，Solari A．Multiple hypothesis testing in genomics．statistics in medicine，2014，33（11）：1946-1978．

［8］Holm S．A simple sequentially rejectivemultiple test procedure Scandinavian Journal of Statistics，1979，6（2）：65-70．

［9］Hochberg Y．A sharper Bonferroniprocedure formultiple tests of significance．Biometrika，1988，75（4）：800-802．

［10］Westfall PH，Young SS．Resampling-Based Multiple Testing：Examples and Methods for P-Value Adjustment．NewYork：W iley-Interscience，1993．

［11］Benjam ini Y，Hochberg Y．Controlling the False Discovery Rate：APractical and Powerful Approach to Multiple Testing．Journal of the Royal Statistical Society，1995，57（1）：289-300．

［12］刘晋，张涛，李康．多重假设检验中FDR的控制与估计方法．中国卫生统计，2012，29（2）：305-308．

［13］Benjam ini Y，Hochberg Y．On the Adaptive Control of the False Discovery Rate in Multiple Testing w ith Independent Statistics．Journal of Educational And Behavioral Statistics，2000，25（1）：60-83．

［14］Benjam ini Y，Krieger AM，Yekutieli D．Adaptive linear step-up procedures that control the false discovery rate．Biometrika，2006，93（3）：491-507．

［15］Yekutieli D．False discovery rate control for non-positively regression dependent test statistics．Journalof Statistical Planning and Inference，2007，138（2）：405-415．

［16］YekutieliD，Benjam ini Y．Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics．Journal of Statistical Planning and Inference，1999，82（1-2）：171-196．

［17］Romano JP，Shaikh AM，Wolf M．Control of the false discovery rate under dependence using the bootstrap and subsampling．Test，2008，17（3）：417-442．

［18］Troendle JF．Stepw ise normal theory multiple test procedures controlling the false discovery rate．Journal of Statistical Planning and Inference，2000，84（1-2）：139-158．

［19］刘莉．两两多重比较的FDR控制．上海：上海交通大学，2015．

［20］Xu H，Gu W，Fan J．Control of the False Discovery Rate Under Arbitrary Covariance Dependence．arXiv：1012．4397，2010．

［21］Fan J，Han X，Gu W．Estimating False Discovery Proportion Under Arbitrary Covariance Dependence．Journal of the American Statistical Association，2012，107（499）：1019-1035．

［22］Leek JT，Storey JD．A general framework formultiple testing dependence．Proceedings of the National Academy of Sciencesof the United States of America，2008，105（48）：18718-18723．

［23］Friguet C，Kloareg M，Causeur D．A Factor Model Approach to Multiple Testing Under Dependence．Journal of the American Statistical Association，2009，104（488）：1406-1415．

［24］Goeman JJ，Solari A．Multiple testing for exploratory research．Statistical Science，2011，26（4）：584-597．

［25］Meinshausen N．False discovery control formultiple tests of association under general dependence．Scandinavian Journal of Statistics，2006，33（2）：227-237．

［26］Hastie T，TibshiraniR，Friedman J．The Elementsof Statistical Learning-Data M ining，Inference and Prediction，2nd edn．New York：Springer，2009，241-245．

［27］王慧．生存分析中半参数模型的变量选择方法及其模拟研究．太原：山西医科大学，2013．

［28］Arlot S，Celisse A．A survey of cross-validation procedures formodel selection．Statistics Surveys，2010，4（0）：40-79．

［29］Nishii R．Asymptotic Properties of Criteria for Selection of Variables in Multiple Regression．Annals of Statistics，1984，12（2）：758-765．

［30］Fan Y，Tang CY．Tuning parameter selection in high dimensional penalized likelihood．Journal of the Royal Statistical Society，2013，75（3）：531-552．

［31］Akaike H．A New Look at the Statistical Model Identification．Automatic Control IEEE Transactions on，1974，19（6）：716-723．

［32］Schwarz G．Estimating the Dimension of a Model．Annals of Statistics，1978，6（2）：15-18．

［33］Foster DP，George EI．The Risk Inflation Criterion for Multiple Regression．Annals of Statistics，1994，22（4）：1947-1975．

［34］Shao J．An asymptotic theory for linear model selection．Statistica Sinica，1997，7（2）：221-242．

［35］Yang Y．Can the strengths of AIC and BIC be shared？A conflictbetween model indentification and regression estimation．Biometrika，2005，92（4）：937-950．

［36］Wang H，LiR，TsaiCL．Tuning Parameter Selectors for the Smoothly Clipped Absolute Deviation Method．Biometrika，2007，94（3）：553-568．

［37］Ternes N，Rotolo F，M ichiels S．Empirical extensions of the lasso penalty to reduce the false discovery rate in high-dimensional Cox regression models．statistics in medicine，2016，35（15）：2561-2573．

［38］Bogdan M，Ghosh JK，Doerge RW．Modifying the Schwarz Bayesian information criterion to locate multiple interacting quantitative trait loci．Genetics，2004，167（2）：989-999．

［39］Bogdan g，M．？S，Ghosh JK．Selecting explanatory variables w ith themodified version of the Bayesian information criterion．Quality＆Reliability Engineering International，2008，24（6）：627-641．

［40］Chen J，Chen Z．Extended Bayesian information criteria formodel selection w ith largemodel spaces．Biometrika，2008，95（95）：759-771．

［41］Wang T，Zhu L．Consistent tuning parameter selection in high dimensional sparse linear regression．Journal of Multivariate Analysis，2011，102（7）：1141-1151．

［42］Meinshausen N，Bühlmann P．Stability selection．Journal of the Royal Statistical Society，2010，72（4）：417-473．

［43］勾建伟．惩罚回归方法的研究及其在后全基因关联研究中的应用．南京医科大学，2014．

［44］Bühlmann P，Kalisch M，Meier L．High-Dimensional Statisticswith a View Toward Applications in Biology．Annual Review of Statistics＆Its Application，2014，1（1）：255-278．

［45］赵俊琴．基于Lasso的高维数据线性回归模型统计推断方法比较．太原：山西医科大学，2015．

［46］Bogdan M，Berg Evd，Su W，et al．Statistical Estimation and Testing via the Ordered L1 Norm．arXiv：1310．1969，2013．

［47］Bogdan M，van den Berg E，SabattiC，et al．Slope-Adaptive Variable Selection Via Convex Optimization．Ann Appl Stat，2015，9（3）：1103-1140．

［48］Su W，Candes E．SLOPE is Adaptive to Unknown Sparsity and Asymptotically M inimax．Ann Appl Stat，2015，44（3）：1038-1068．

［49］Barber RF，Candès EJ．Controlling the false discovery rate via knockoffs．Annals of Statistics，2014，43（5）：2055-2085．

［50］Reid S，Tibshirani R．Sparse regression and marginal testing using cluster prototypes．Biostatistics，2016，17（2）：364-376．

［51］Barber RF，Candes EJ．A knockoff filter for high-dimensional selective inference．arXiv：1602．03574，2016．

［52］Verweij PJ，Van Houwelingen HC．Cross-validation in survival analysis．statistics inmedicine，1993，12（24）：2305-2314．

（责任编辑：郭海强）

国家自然科学基金项目（81473073）

△通信作者：王彤，E-mail：tongwang＠sxmu．edu．cn