基于Kernel_PCA算法的中医药项目执行情况综合评估*

湖北中医药大学信息工程学院（430065） 黄 瑶 肖 勇

基于Kernel_PCA算法的中医药项目执行情况综合评估*

湖北中医药大学信息工程学院（430065） 黄 瑶 肖 勇△

近年来，中央财政用于支持全国中医药事业发展的专项资金屡创历史新高，财政部等部门对中医药项目预算执行管理提出更高的要求［1-2］。中医药项目数据并不存在直接的线性关系，应用单一指标使用的评估方法很难直接和全面反映全国中医药项目总体执行情况。Kernel_PCA算法不是一种新型算法，它是由主成分分析法（principal component analysis，PCA）进一步发展而来，可处理非线性数据，通过非线性映射将初始数据空间投射到高维特征空间，然后在特征空间里进行主成分分析，把非线性问题转化为线性问题。本文基于Kernel_PCA算法，综合考虑全国各省份中医药项目的预算执行情况，运用多重填补法（multiple imputation，M I）对中医药项目数据进行预处理，采用多目标综合优化思想，凝炼得到综合评估，并将最终结果与现实情况对比验证［3］。

M I与Kernel_PCA概述

本文研究的中医药项目执行数据存在某些项目无预算而导致数据缺失，因此对中医药项目执行数据降维处理前需要进行预处理。本文采用M I法，其定义如下［4-6］：M I法是通过某种方法对每一个缺失值都构造m个插补值（m≥2）产生m个完整数据集，这些值也反映了缺失值的不确定性，然后用分析完整数据集的统计学方法进行研究，在得到目标变量的估计前对这些结果进行综合考量，使得出的结论更合理、可靠［7-9］。目前，M I法主要应用在社会科学、行为学和生物医学等领域［10］。PCA是最小均方误差意义上基于数据间的线性关系提取数据主要特征分量，是常用的高维数据降维算法之一，但PCA不能处理具有非线性性质的数据［11-14］。Kernel_PCA（Kernel Principal Component Analysis），也称核主成分分析，由Scholkopf等人提出，是一种非线性主成分提取方法，基本思想是构造一个满足Mercer条件的核函数，通过非线性映射将初始输入空间R的数据集投影到高维特征空间F，然后在高维空间对映射数据做PCA处理，这个新空间可以增加数据的线性可分性，具有很强的非线性处理能力［15-16］。Kernel_PCA的核心在于核方法对PCA的非线性推广，能有效捕捉数据的非线性特征，主要用于人脸识别、手写体数字去噪、机器学习、模式识别、数据压缩、图像去噪、语音信号处理和函数逼近等领域［11，17-18］。

Kernel_PCA算法的实现过程如下：

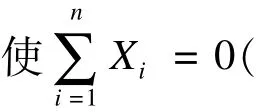
对于一般的PCA方法，即通过求解特征方程获得贡献率最大的特征值及与之相对应的特征向量：

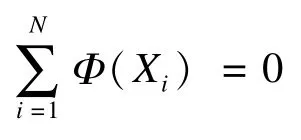
在特征空间中的PCA是求解下列方程的特征值和特征向量，代入式（2）中得：

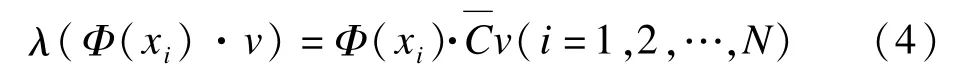
由于特征向量可以由数据集线性表示，则v可以由Φ（xk）（k＝1，2，…，N）线性表示，即：

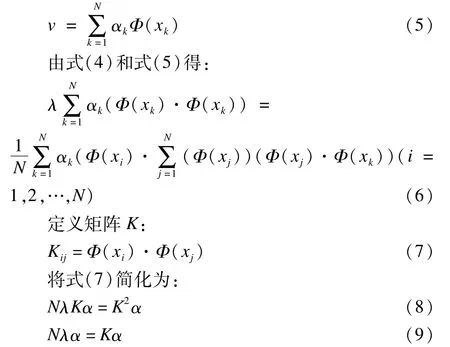
通过对式（9）的求解，即可获得要求的特征值和特征向量。

综合评估实现过程

1．实现步骤

根据上述思想路线，给出中医药项目的Kernel_ PCA算法综合评估方法和步骤：

Step 1.将全国15个省份按1，2，…，15依次编号，将2011年到2015年中医药项目的所有中医药子项目按1，2，…，8依次编号，表中数据项代表的是中医药项目的预算执行率（为方便数据处理，全部用0～1的数表示），将原始数据简化为5张只含有数值和编码的表。

Step 2.剔除所有项目都缺失的省份以及数据缺失大半的项目，将剩下省份、项目重新依次编号。通过多重填补法处理部分省份部分项目因无预算而缺失的数据，得到一系列完整数据集。

Step 3.将若干个完整数据集采用Kernel_PCA算法进行处理，得到相对应的若干组结果。

Step 4.为消除结果中正负值相互抵消的影响，根据每组结果进行评估排序，得到相应的若干组排序值（无正负）。

Step 5.经计算得到每组排序值的求和平均值，最终得到一组数据，再进行排序，则最后得到的一组数据就能反映全国各省中医药项目的综合评估情况。

2．数据处理

根据需要搭建相应的平台环境，利用Excel 2010、MATLAB（R2014a）和SPSS 19．0分析工具，对原始数据进行加工、处理等适当操作得到最终结果，如图1所示：

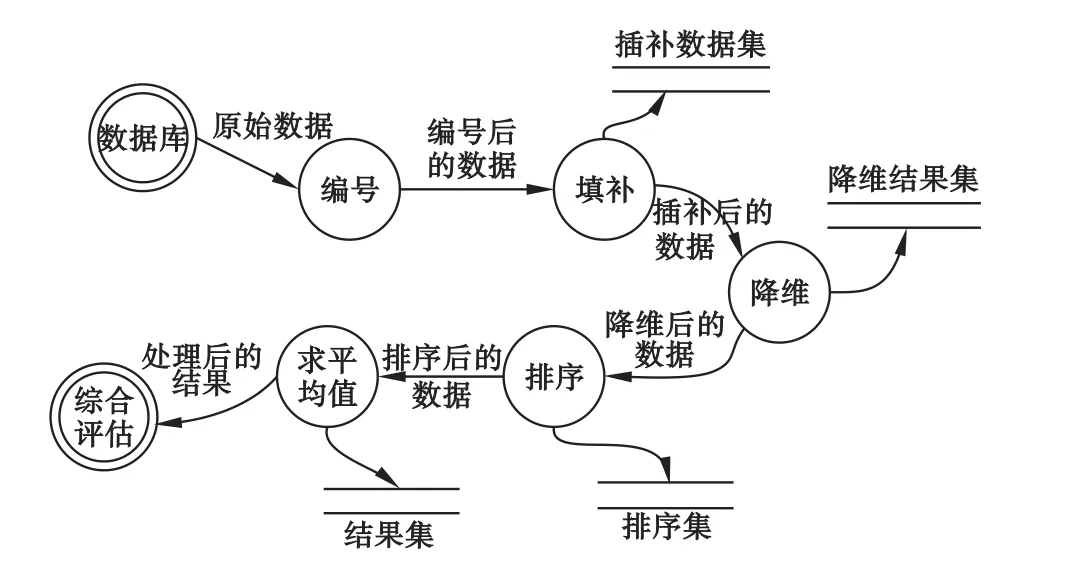
图1 数据流图

表1是利用SPSS 19．0分析软件来对编码后的数据进行多重填补，采用的是MCMC填补方法，根据对数据的分析处理以及其他学者对缺失值方法对比研究得出的一致结论：M I优于EM、回归插补法等方法，采用M I方法填补数据，再按照实现步骤中的step3～5，对每个由降维算法得出来的结果进行排序，得到结果如表2所示。

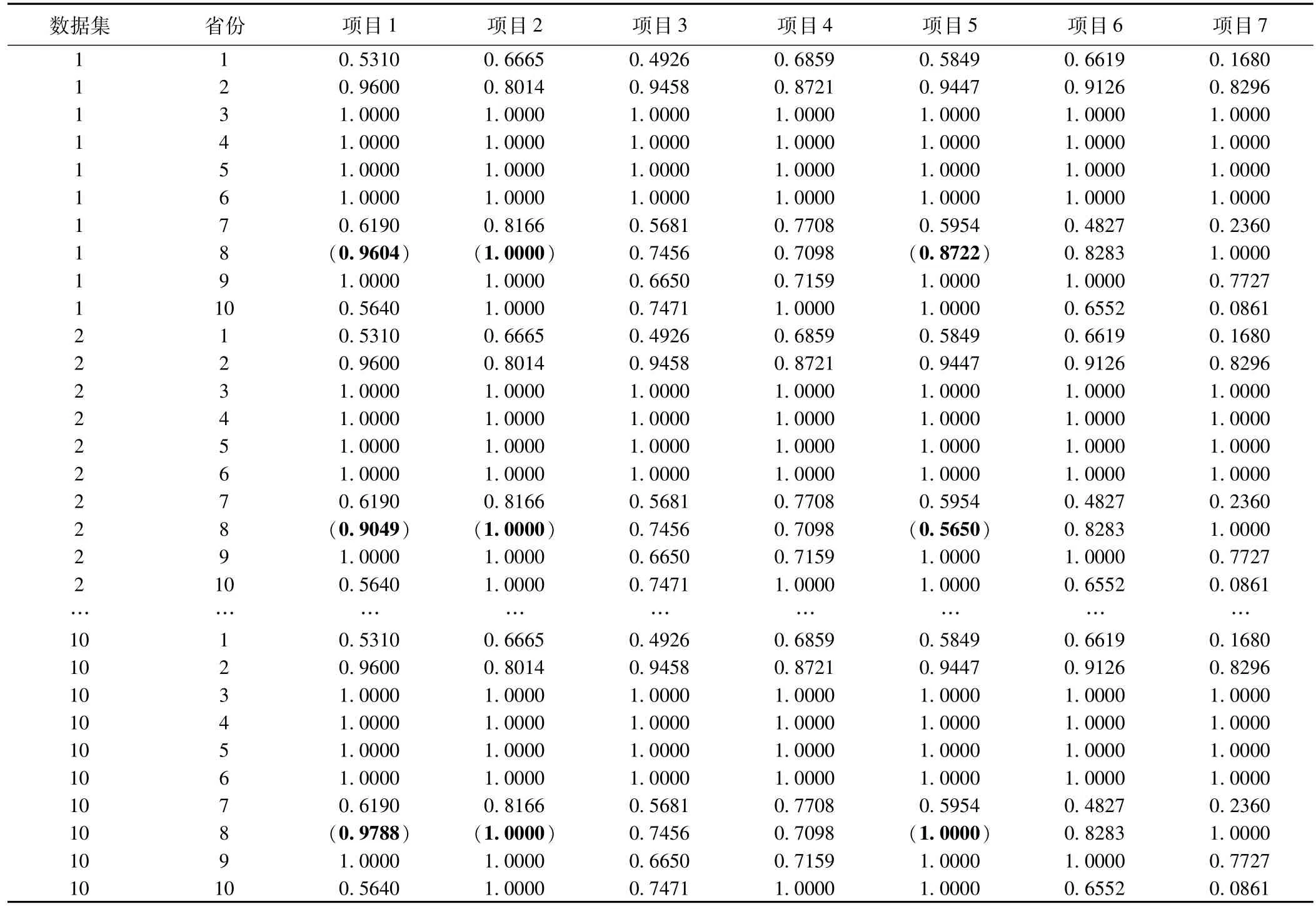
表1 2014年中医药项目插补数据集

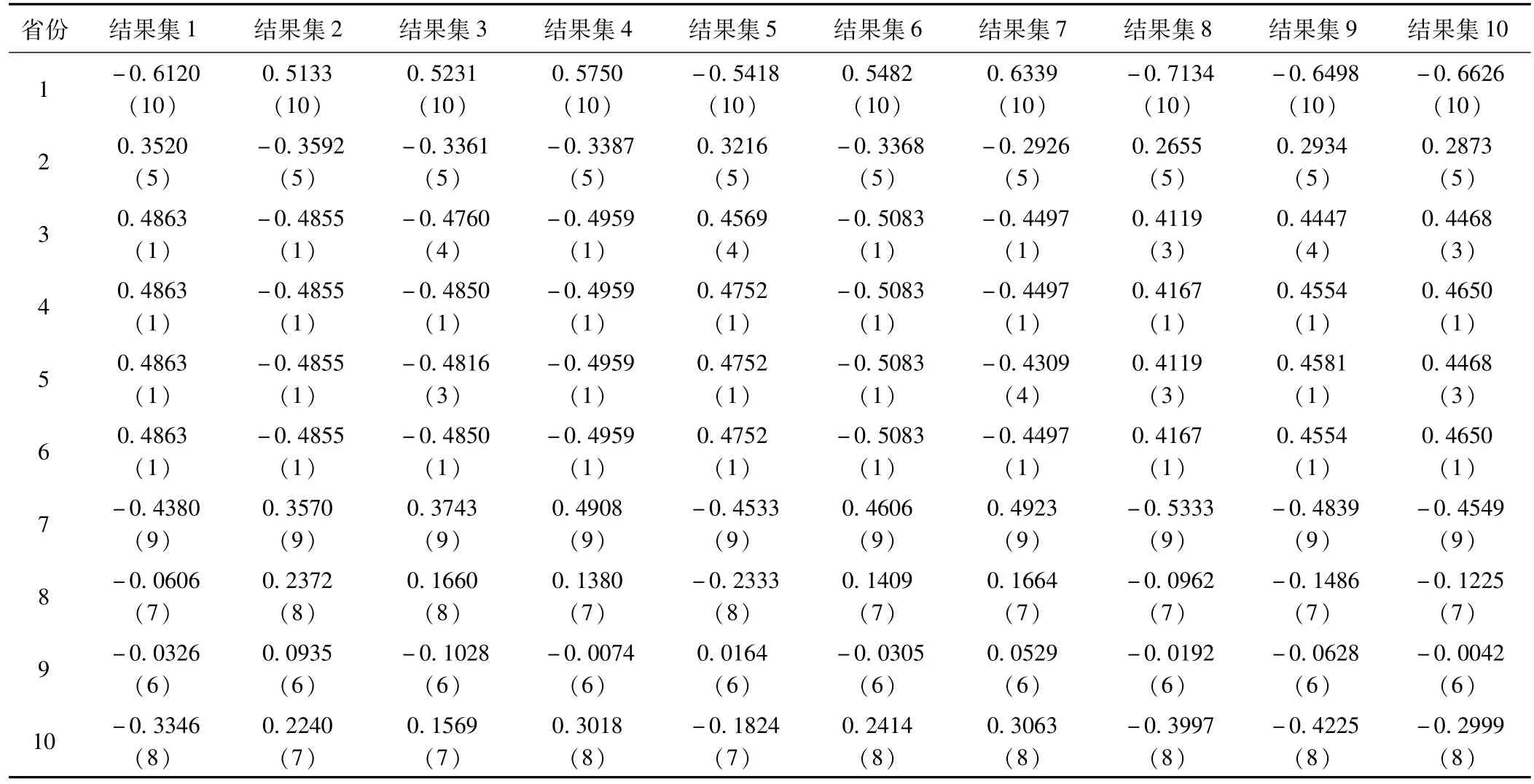
表2 2014年中医药项目降维结果集（排序集）

3．综合排名

根据表2计算出2014年各省总排名，同理可计算出其他年份各省总排名，得到最终结果如表3所示：

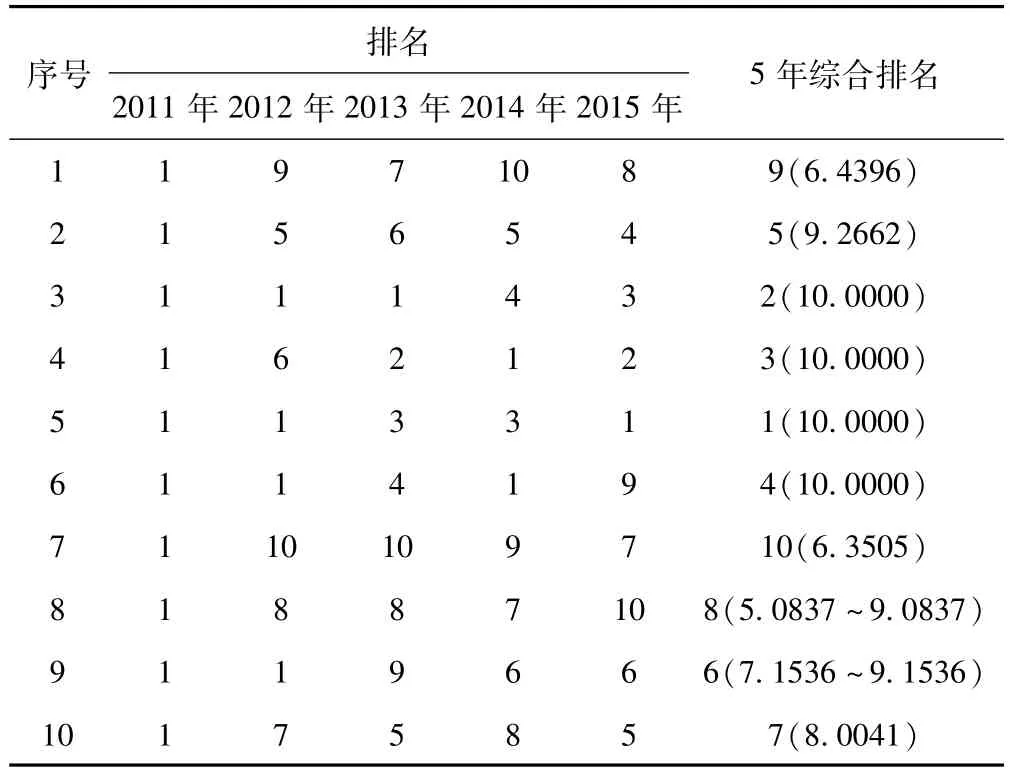
表3 2011-2015年中医药项目综合评估表

结 果

从表3可知，本文评估方法综合了所有中医药子项目的结果，最终认为编码为3、4、5、6省份的中医药项目综合执行情况较好，数据处理结果与现实情况（由执行率可知，编码3、4、5、6省份的执行率之和均为10．0000，执行情况较好；编码1、7省份执行情况较差）基本保持一致，证明了该研究思路的合理性、有效性和准确性［19-20］。

讨 论

本文提出基于Kernel_PCA算法的中医药项目综合评估，采用M I进行数据填补，这是经过处理分析选择的方法（笔者还采用了条目均数填补法、自身均数填补法等方法，比较而言，M I处理的结果更接近完整数据的分析结果，由于篇幅限制，本文对其他方法不展开过多阐述），然后利用非线性数据压缩特征空间维数的特性，综合了所有中医药子项目的复杂执行情况，能较好地全面反映全国各省中医药项目执行情况的差异和中医药项目整体情况，避免目前用于中医药项目评估的方法单一导致结果片面性较强，不利于对中医药项目的整体把握。因此本文探索新方法进行分析，更好地为中医药项目决策提供科学依据。基于Kernel_PCA算法综合评估的最终结果也与实际判断一致，表明该方法思路的有效性、可行性，可进一步推广到其他相关项目的综合评估。

［1］刘晶．中医药项目经费预算执行监控通报平台的分析与设计．湖北中医药大学，2012：82．

［2］黄橙紫，王振宇，田双桂，等．中医药项目绩效管理现状与对策探析．中医药管理杂志，2014，33（12）：1969-1971．

［3］田双桂．中央转移支付中医药项目预算执行分析和对策研究．湖北中医药大学，2014．

［4］Duan YJ，Lv YS，Kang WW，etal．A Deep Learning Based Approach for Traffic Data Imputation．Proceedings of 17th International IEEE Conference on Intelligent Transportation SystemsⅡ．2014．

［5］Wang Y，Zhang ZC，Tian ZX，et al．Preprocessing the M issing Data for Environmental Prediction Model Based on Multiple Imputation．Proceedings of 2012 International Conference on Power Electronics Engineering and Computer Technology（PEECT 2012）．2012．［6］Li L，Su XN，Zhang Y，et al．Traffic Prediction，Data Compression，Abnormal Data Detection and M issing Data Imputation：An Integrated Study Based on the Decomposition of Traffic Time Series．Proceedings of 17th International IEEE Conference on Intelligent Transportation SystemsⅠ．2014．

［7］帅平，李晓松，周晓华．缺失数据统计处理方法的研究进展．中国卫生统计，2013，30（01）：135-139．

［8］王睿，马修强，陆健．Epworth量表中缺失数据处理方法研究．中国卫生统计，2013，30（01）：72-73．

［9］佟昕，高强．统计学中的数据缺失及解决方法．辽宁经济管理干部学院（辽宁经济职业技术学院学报），2011（02）：15-16．

［10］邹莉玲，吴娟丽，李觉．多重填补法在任意缺失随访资料中的应用．中国卫生统计，2015，32（02）：221-223．

［11］薛冰．Kernel PCA中核参数优化及应用．西安工业大学，2011．

［12］徐涛，孙彤．基于KPCA的非线性ASM定位方法研究．微电子学与计算机，2010，27（12）：113-116．

［13］刘进，邓家刚，覃洁萍，等．基于红外光谱数据的中药药性识别研究．时珍国医国药，2010，21（03）：561-563．

［14］徐明亮，孙长海，王瑜等．基于主成分分析的决明子电化学振荡指纹图谱的评价研究．时珍国医国药，2011，22（08）：1858-1859．

［15］Ling A，Yi Z，Ye S．Model Reduction for Spatio-temporal Systems based on KPCA and LS-SVRM．第25届中国控制与决策会议论文集．2013．

［16］Peng HX，Wang R．Sensor Fault Detection and Identification using Kernel PCA and Its Fast Data Reconstruction．Proceedings of 2010 Chinese Control and Decision Conference．2010：3857-3862．

［17］沈徐辉，罗小平，杜鹏英．基于模糊的改进KPCA方法：第二十九届中国控制会议，中国北京，2010．

［18］赵英男，王水平，郑玉．一种基于数值逼近的KPCA改进算法．南京信息工程大学学报（自然科学版），2012，04（04）：362-365．

［19］赵小强，王新明．基于改进核主元分析的TE过程故障诊断．工业仪表与自动化装置，2010（03）：7-11．

［20］胡淼，董方，田丽娟，等．应用因子分析法探讨新型农村合作医疗绩效评价．中国卫生统计，2016，33（1）：24-26．

（责任编辑：邓 妍）

湖北省教育厅人文社会科学研究项目（17Q098）；中医药项目绩效考核数据分析关键算法研究

△通信作者：肖勇，E-mail：15327455586＠126．com