多组学联合缺失数据填补方法的评价*

南京医科大学公共卫生学院生物统计学系（211166） 董学思 林丽娟 赵 杨 魏永越 戴俊程 陈 峰

多组学联合缺失数据填补方法的评价*

南京医科大学公共卫生学院生物统计学系（211166） 董学思 林丽娟 赵 杨 魏永越 戴俊程 陈 峰△

目的 本研究旨在评价不同平台间“块缺失”数据的填补方法。如何在保证方差-协方差结构相对稳定的前提下提高多组学数据填补的精确度，对于后期数据挖掘有重要的意义。方法 利用癌症基因组图谱（TCGA）数据库的肺癌数据（甲基化数据、基因表达数据），构建不同缺失比例的数据集（缺失比例分别为5%、20%、35%、50%和65%）。采用统计学填补方法均值法，马尔科夫蒙特卡洛法（MCMC）和机器学习填补法［邻近法（kNN），随机森林法（RF），多层感知机法（MLP）］对缺失数据进行填补，填补后数据集与原数据集进行比较。评价指标包括估计偏差和矩阵-2-范数。根据评价指标和填补时间，比较出填补效果最优、填补时间较短的方法。结果 MLP和kNN算法在各种缺失比例下均比其他填补方法有更优的效果，填补时间也相对较短。均值法的时间最短，在数据集缺失比例较小时（≤5%），填补效果与其他填补方法相当，但在高比例缺失情况下表现较差。在数据集高比例缺失情况下，RF和MCMC的填补效果优于均值法，但填补时间过长，不适用于实际工作。结论 综合比较，机器学习填补方法中的MLP和kNN两法适合于甲基化数据和表达数据的填补。

多组学数据 块缺失 统计学填补 机器学习填补 效果评价

生物数据的获取受限于现阶段技术手段所存在的不足（测序过程中对比基因组测序误差、芯片划痕、图像污染等），缺失数据的产生不可避免［1］。高维生物数据研究中，由于样本数据往往存在不同平台的测量信息，在样本信息匹配时，经常存在有部分样本缺失某平台数据的情况——“块缺失”。

传统上，研究者在探索缺失值填补方面更侧重于统计填补法，该类方法虽简单易行，却难以挖掘数据之间的深层关系，填补效果并不理想［2］；国外近几年在机器学习领域的填补方法研究较多，该类方法对数据分布类型不敏感，通过计算机模拟的形式深入挖掘数据结构关系，填补效果较优［4］。现阶段，数据填补的主要手段均基于以上两大类方法（统计填补、机器学习填补），国内研究者进行过一系列统计填补方法的效果评价，但对统计填补方法和机器学习填补方法的比较并不多见。

本研究通过构建不同缺失比例的数据集，采用统计填补法和机器学习填补法进行填补，采用估计偏差和矩阵-2-范数作为评价指标，比较填补效果，选出优势方法。不同平台数据之间的填补将会提高信息利用率，提高检验效能，有助于研究者得到更可靠的结果。

数据与方法

1．数据

选择癌症基因组图谱（TCGA）公共数据库的肺癌甲基化、基因表达数据，将含有缺失变量的样本剔除，保留完整样本，便于填补效果比对。选择肺癌经典生物通路WNT通路中基因表达变量141个，甲基化位点3962个，样本782例，作为第一个研究数据集［5］；再按照同样的变量类型和变量数，从全基因组中随机抽取141个基因表达变量和3962个甲基化位点，保留完整样本880例，作为第二个数据集。将两个数据集按5%、20%、35%、50%、65%的样本缺失比例构造缺失，缺失部分样本的选择为完全随机，避免偶然性。其中，缺失的样本中50%样本的表达数据缺失，50%样本的甲基化数据缺失，即在不完整观测中，缺失甲基化数据的样本拥有完整的基因表达数据；缺失基因表达数据的样本拥有完整的甲基化数据。这样的缺失比例更加符合“块缺失”的数据情况。在接下来的填补工作中，笔者将用甲基化数据对表达数据进行填补，用表达数据对甲基化数据进行填补。

本研究利用这两个数据集，保证在相关结构和非相关结构数据集中填补方法的稳定性，这样构建的相关结构更贴近实际情况。将各种缺失比例的数据集进行5种填补方法的填补，每种方法填补100次，将填补后数据集与原数据集进行对比，并计算综合评价指标，评价填补效果。模拟试验流程见图1。

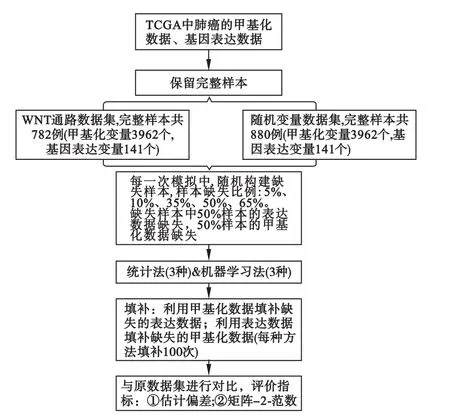
图1 模拟试验流程

2．方法

此次研究采用统计填补法和机器学习填补法：分别是均数法（mean）、马尔科夫蒙特卡洛法（Markov Chain Monte Carlo，MCMC）、随机森林法（random forest，RF）、K邻近法（k-nearest neighbor，kNN）和多层感知机法（multi-layer perceptron，MLP）。均值法是最经典的填补方法之一，简便易行。MCMC填补在之前研究中被广泛提及，因其能充分利用完整数据部分作为先验，因此填补的效果往往高于常见的统计方法填补。机器学习的三种填补方法在单一数据集填补的研究中有过报道，但尚未应用于多组学数据的填补中。

（1）统计填补

①均值法（mean）

采用缺失变量非缺失部分的均值对缺失部分进行填补，填补方法简单，填补时间极短，但未考虑到数据本身变异性，降低填补后数据方差，破坏原有数据结构。其步骤可以整理为：计算缺失变量中非缺失部分的均值；所计算均值代替缺失数据。

②马尔科夫蒙特卡洛填补（MCMC）

MCMC利用变量均值向量和方差-协方差阵作为先验信息，构建马尔科夫链，保证其元素的分布可以收敛到一个平稳分布，通过抽样反复模拟该马尔科夫链，得到平稳的后验分布，产生缺失数据的估计［6］。其步骤可以整理为：

a将数据集拆分为完整观测部分Xfull和不完整观测部分Xmiss。

μ＝［μ′1，μ′2］代表Xfull和Xmiss的均值向量；∑11、∑22分别代表Xfull、Xmiss的方差-协方差矩阵，∑12代表Xfull和Xmiss的方差-协方差矩阵；

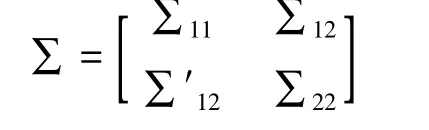
b给定Xfull＝X1，Xmiss的均向量为μ2．1＝μ2+∑′12∑′11（X1-μ1）；相应条件协方差矩阵为∑22．1＝∑22-∑′12∑-1

11∑12；c给定Xfull，从Xmiss的条件分布中随机抽取数值，对缺失部分进行填补；

d经过填补后，产生完整数据集，循环上述步骤，估算新产生的均向量和协方差矩阵进行填补，直至收敛。

（2）机器学习填补法

①随机森林填补（RF）

RF填补应用集成决策树的思维，完全分裂产生回归树，每一棵分类树代表一个多元非线性模型，产生缺失变量的加权平均值，对缺失数据进行填补［3］。其步骤可以整理为：

a将完整数据部分作为自变量，缺失数据部分作为预测变量；

b在数据集中采用Bagging的方法，随机抽取部分的样本作为单棵决策树的训练集；

c按照完全分裂构造决策树回归器，每棵树产生一批填补值，最后将各棵树的结果取平均值，作为填补值进行填补。

②K邻近填补（kNN）

kNN填补在样本数据集的特征空间中，按照马氏距离选取相近（即特征空间中邻近）的样本集，计算对应变量的加权平均值进行填补。相较均值填补，kNN考虑了样本间的变异，保持了数据结构的稳健性［7］。其步骤可以整理为：

a构建完整样本集的矩阵结构；

b计算含有缺失变量的样本集Xmiss与完整样本集Xfull中各样本的马氏距离；

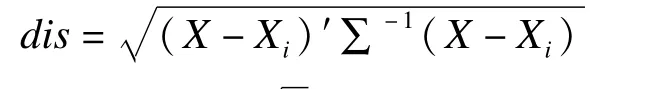
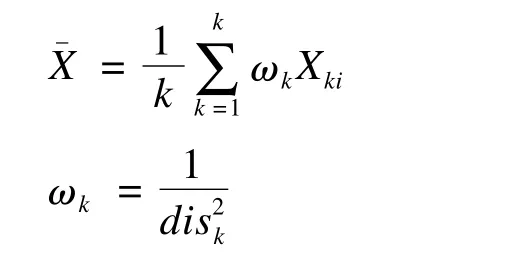
d所计算的均值代替缺失数据。

③多层感知机填补（MLP）

MLP是人工神经网络的重要分支，通过训练集样本训练神经网络结构，经多次层间映射，产生缺失变量估计值［8］。MLP尤其适用于混合分布数据库，在高维多平台数据中，可以综合不同平台信息训练构建人工神经网络结构，进行缺失数据填补。本次研究采用标准的三层单向神经网络结构：第一层为输入层，输入某样本完整部分的变量；第二层为隐藏单元；第三层为输出层，产生缺失数据的估计值，见图2。层间由权重矩阵连接，输入层经过隐藏单元层映射至输出层，产生填补值。其步骤可以整理为：

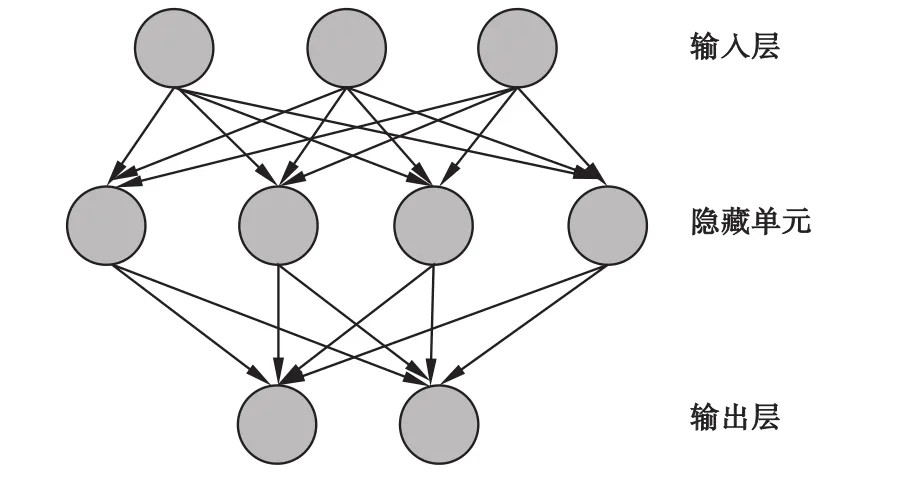
图2 多层感知机网络结构

a构建完整数据集矩阵Xfull，作为训练数据集，含有缺失变量的样本作为预测集Xmiss；

b采用剪枝算法，交叉验证，计算隐藏单元数目；

c采用共轭梯度法，计算层间权重向量；

d根据输入向量，通过映射函数映射至隐藏单元：

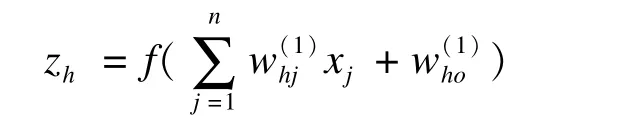
zh是隐藏单元，h＝1，…，h，hj是第一层权重矩阵，who是残差项，f（）为激励函数，通常为双曲正切函数或logit函数；

e隐藏单元再经过一次激励函数转化至输出层。yk是输出单元k＝1，…，k，wkh是第二层权重矩阵，wko是残差项，g（）为线性激励函数：

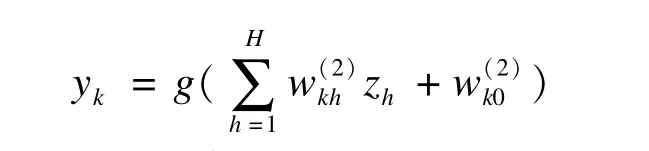
f产生神经网络结构；

g输入预测集样本Xmiss，估计预测集中缺失数据。

5种方法的填补效果用估计偏差和矩阵-2-范数来评价。估计偏差：原数据集中变量均数，与填补后数据集中变量的均数之差的绝对值之和，再取平均值。可定义为：

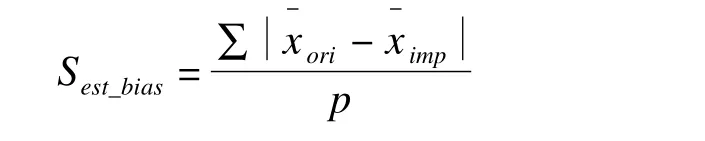
其中，x-ori为原数据集中各变量的均值，x-imp为填补后的数据集中各变量的均值，p为变量数。该指标反应填补的精确度，估计偏差越小，填补的精确度越高。

矩阵-2-范数：转置矩阵d’与原矩阵d的积的最大特征根的平方根值。几何意义指空间上两个矩阵（向量）的距离。待比较的两个矩阵作差得矩阵d，求得矩阵-2-范数，反映的是差值矩阵距离原点的距离，即：方差-协方差矩阵变化幅度，可定义为：

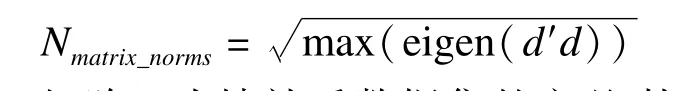
矩阵d为填补后数据集的方差-协方差矩阵与原数据集方差协方差矩阵的差，eigen（）函数分解矩阵特征根，max（）函数求得最大特征根。该指标反映的是填补数据集与原数据集的数据结构变化幅度，矩阵-2-范数越大，数据结构的变化越大，反之则小。

本研究模拟试验采用Linux shell进行数据整理，填补过程采用R语言编程实现，主要工具包为“RSNNS”和“missForest”。

结 果

1．估计偏差

图3和图4分别是WNT通路变量数据集和随机变量数据集填补之后的估计偏差。由图3和图4可知，5种填补方法在填补精度上均随着缺失数据比例的升高而降低，但MLP和kNN的稳定性较高，在各种缺失比例情况下均高于其他填补方法。RF和MCMC方法估计偏差接近，二者均高于均值法。均值法随着缺失比例的升高，对填补精度的损失比较大。

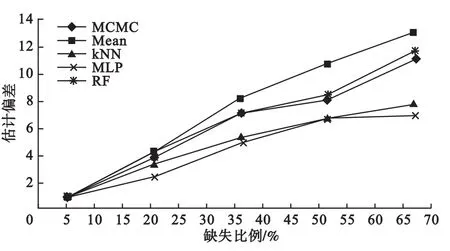
图3 5种填补方法在WNT通路数据集中的估计偏差

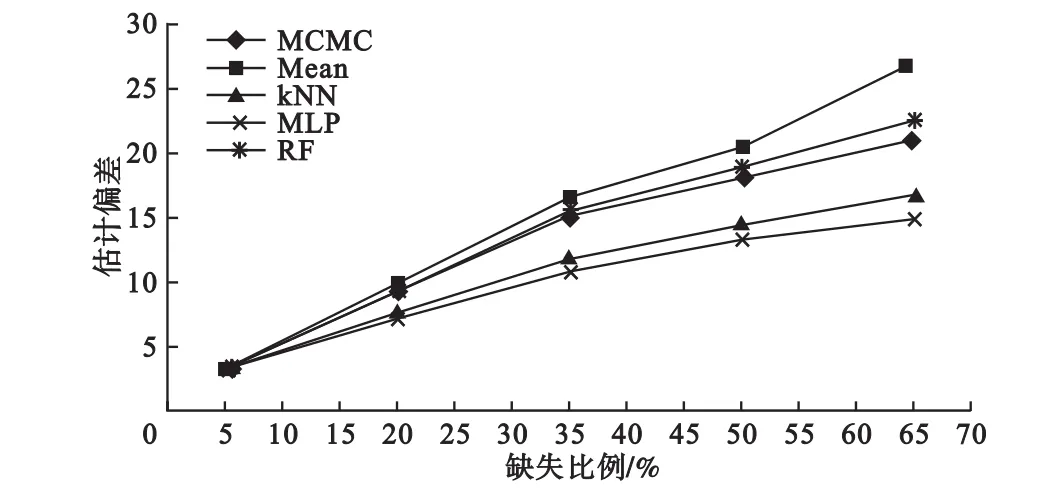
图4 5种填补方法在随机变量数据集中的估计偏差

2．矩阵-2-范数

由图5和图6可知，在WNT通路变量数据集和随机变量数据集中，MLP和kNN填补更加稳健，均值填补则倾向于破坏原有数据结构（变异被低估）。MCMC和RF填补在维持数据结构方面亦优于均值填补，但是不及MLP和kNN。

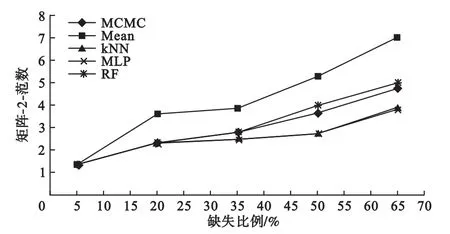
图5 5种填补方法在WNT通路数据集中的矩阵-2-范数

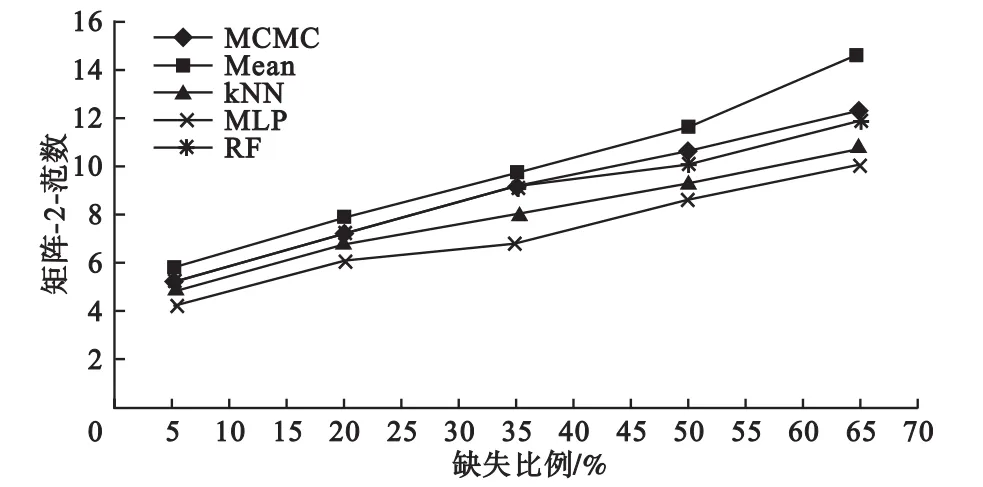
图6 5种填补方法在随机变量数据集中的矩阵-2-范数

估计偏差和矩阵-2-范数从两个方面评价填补效果，即填补精度和数据结构稳定性。然而，在实际高维数据挖掘工作中，对缺失数据的填补，还要考虑到填补效率的高低，见图7。MCMC和RF填补在5种填补方法中耗时最长，且效果不及MLP和kNN。因此，不推荐应用这两种方法。得益于填补值计算的简便，均值填补的填补时间最短。但均值填补的填补效果差强人意，亦不做推荐。MLP和kNN填补的填补效率高，以上两种方法无论在估计偏差还是矩阵-2-范数方面，均表现优异，同时，填补时间仅高于均值填补。

讨 论

本研究中，根据评价指标和填补时间，读者可以发现：kNN和MLP方法的填补效果要优于均值法、MCMC以及RF。究其原因，kNN和MLP方法对于数据的分布类型并不敏感，稳定性较好［8-9］，因此保证了在数据为多平台来源时，填补效果较为可靠。基于实际应用考虑，虽然RF和MCMC的填补效果优于均值法，但由于填补时间过长，不推荐RF和MCMC方法用于填补。均值法在数据缺失比例很低的情况下（≤5%）亦可以起到比较好的填补效果，同样值得应用。

在RF填补中，RF的每一棵树代表一个独立的非线性模型，多个模型组成的随机森林在抗过拟合方面较单个模型更加可靠，但在一些噪音较大的回归问题上，RF也会陷入过拟合，Weiss曾深入讨论过此问题［10］。MCMC过程依赖于反复的模拟，形成足够长的马尔科夫链，对于高维的非线性数据，其效果有待商榷［11］。笔者推荐的两种机器学习方法对于多平台生物数据，有较好的稳健性和容错性，能够在不依赖数据分布类型的情况下映射高维非线性复杂数据。MLP算法在层间权重矩阵的设定方面采用共轭梯度法，该方法不但克服了最速下降法收敛慢的弊端，也规避了牛顿法大量的矩阵运算过程，同时又不需要任何外来参数，是处理非线性高维数据最有效的方法之一。kNN算法通过属性空间距离的最相近，构造目标变量的候选集合，该方法对异常值不敏感，计算时间也相对较短。MLP和kNN两种方法不仅适用于数值拟合，在判别分类方面亦有稳定可靠的表现。鉴于以上两类方法分别在隐藏单元个数和k值方面不能自适应，需要预先设定，亦有研究者在MLP中采用隐藏单元个数等于训练集样本数，在kNN中k值等于训练集样本数的平方根的方法［12］。

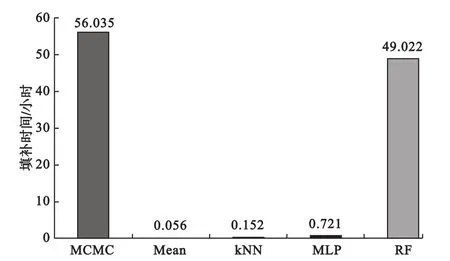
图7 5种填补方法填补时间对比

根据研究结果，不难发现，无论何种方法，在缺失比例升高的情况下，填补效果必然下降。当缺失比例高于70%时，填补效果较差，因此本研究未作更高缺失比例情况下的讨论。“块缺失”数据可分为两种情况：①测有某平台的变量数据的样本中，部分样本不含有另一平台的数据；②测有某平台的变量数据的样本中，所有样本完全不含有另一平台的数据。本研究主要讨论了第一种情况。在第二种情况中，几乎难以从现有数据中挖掘信息用于填补，此种情况下，只能从其他数据库获取先验信息，当获得信息足够充分时，填补效果才能可靠，此情况有待进一步研究。

多组学数据的“块缺失”也是完全随机缺失的一种形式，对于其他缺失机制，并未作讨论。矩阵-2-范数作为评价填补后数据集与原数据集中数据结构变化的指标，考虑了矩阵之间的差异度，但是矩阵-2-范数仅用到最大特征根，也是本指标的一个局限，有待后续继续研究。

［1］邱浪波，王广云，王正志，等．基因表达缺失值的加权回归估计算法．国防科技大学学报，2007，29（1）：111-115．

［2］张桥，李宁，张秋菊，等．任意缺失模式缺失数据不同填补方法效果比较．中国卫生统计，2013，30（5）：690-692．

［3］吴俊杰，赵鹏．非线性噪声数据集上基于随机森林的空缺值填补算法．计算机应用与软件，2013，30（7）：51-53．

［4］W illiam S，Chad E，Herman T．Machine learning data imputation and classification in amulticohorthypertension clinical study．BioinformBiol Insights，2016，9（3）：43-54．

［5］Han D，Cao C，Su Y，etal．Ginkgo biloba exocarp extracts inhibits angiogenesis and its effects onWnt／beta-catenin-VEGF signaling pathway in Lewis lung cancer．J Ethnopharmacol，2016，192（1）：406-412．

［6］M ikhchi A，Honarvar M，Kashan NE，et al．Assessing and comparison of different machine learning methods in parent-offspring trios for genotype imputation．JTheorBiol，2016，399（2）：148-158．

［7］Beretta L，Santaniello A．Nearest neighbor imputation algorithms：a critical evaluation．BMC Med Inform DecisMak，2016，16（3）：63-74．

［8］Jerez JM，Molina I，García-Laencina PJ，et al．M issing data imputation using statistical and machine learning methods in a real breast cancer problem．ArtifIntell Med，2015，50（2）：105-115．

［9］Bibault JE，Giraud P，Burgun A．Big Data andmachine learning in radiation oncology：State of the art and future prospects．Cancer Lett，2016，382（1）：110-117．

［10］Weiss GM．M ining with rarity：A unifying framework．JSIGKDD Explorations，2004，6（1）：7-19．

［11］RiviereMK，Ueckert S，Mentre F．An MCMC method for the evaluation of the Fisher informationmatrix for non-linearmixed effectmodels．Biostatistics，2016，17（4）：737-750．

［12］BrettL．机器学习与R语言．李洪成，许金炜，李舰译．机械工业出版社，2015：45-50．

（责任编辑：郭海强）

Evaluations on Several Im putation Approaches of Integrated Omics Data

Dong Xuesi，Lin Lijuan，Zhao Yang，et al（Department of Biostatistics，School of Public Health，Nanjing Medical University（211166），Nanjing）

Objective In post-GWAS era，integrated data from various platforms has become increasingly popular．Because of the complexity of data sources，many new challenges arise，which inevitably include how to treat“block missing data”．Ensuring the imputation accuracy and precision as well asmaintain the variance-covariance structure of the original data is of great importance to missing data imputation．In this project，we aimed to evaluate the effect of several imputationmethods based on both statistical techniques and machine learning techniques，on the integrated data from different data-platforms．Methods We go tlung cancer data-set（DNA methylation and gene expression）from The Cancer Genome Atlas（TCGA），and constructed m issing data-setw ith differentm issing proportions at5%，20%，35%，50%and 65%．The statisticalmethods（Mean imputation method，MCMC）and machine learningmethods（kNN，MLP，RF）were applied．Evaluation indicators included estimation bias and matrix 2-norms．At last，we considered imputation time and finding out a time-saving and efficientmethod．Results MLP and kNN showed high quality imputation effectand less time consuming from differentmissing ratio．Mean imputation had shortest filling time，and the imputation quality was high whenm issing ratio was low（≤5%）．However，whenmissing ratio increasing，the imputation effect decreased．When them issing ratio increasing，RF and MCMCmethod exceled in Mean approach．Nevertheless，RF and MCMC were time-killer．Conclusion After comprehensive comparative analysis，MLP and kNN imputation from machine learningmethods turned out to be suitable approaches in joint imputation process（DNA methylation，gene expression）．

Integrated omics data；Block m issing data；Statistical imputation；Machine learning imputation；Evaluation

本课题受国家自然科学基金重点项目（81530088）、面上项目（81473070，81373102）、国家自然科学青年基金（81402764）以及江苏省高校优势学科资助

△通信作者：陈峰，E-mail：fengchen＠njmu．edu．cn