基于BackStepping的全向机器人编队控制

王钦钊，程金勇，李小龙

(装甲兵工程学院 控制工程系， 北京 100072)

【信息科学与控制工程】

基于BackStepping的全向机器人编队控制

王钦钊，程金勇，李小龙

(装甲兵工程学院 控制工程系， 北京 100072)

提出一种多机器人协同编队方法；根据领航机器人和队形库确定虚拟领航者的位姿参数，将基于领导跟随方法的编队问题转化为跟随机器人对于虚拟领航者的轨迹追踪问题；采用BackStepping方法逐步构造控制系统的Lyapunov函数，使该函数负定，跟随机器人全局渐进的跟踪各自的虚拟领航者；仿真和实物实验验证了该编队方法的有效性与可行性。

全向机器人；BackStepping；编队；轨迹跟踪

随着机器人应用领域的扩展，单机器人由于自身的局限性，对于复杂的任务和多变的环境而言，能力稍显不足。人们受到鸟类、鱼群、蜂群等生物种群合作行为的启发，逐步开始考虑多个机器人协调协作完成任务。与单机器人相比，多机器人系统具有更强的工作能力，在资源勘探、安全巡逻、智能交通和大型物体运输等方面都有非常广泛的应用前景。

多机器人编队控制是指多个机器人向目标运动的过程中，既能够收敛于特定的队形，又能够适应外界环境约束[1]。目前多机器人的编队控制方法主要有虚拟结构法、领导-跟随方法、人工势场法、基于行为的方法等。基于虚拟结构的队形控制方法结合图论拓扑理论，以刚体上的点引导相应的机器人形成编队，任一机器人故障或者失效都有可能导致编队失败。人工势场法需要对每种队形设定相应的势场函数，复杂队形的势场函数构建比较困难。基于行为方法适应于不确定环境且实现比较简单，但是队形不够精确，难以进行精确的数学描述。领导—跟随方法控制方式较为简单，易于工程实现和编队误差的分析。文献[2]分析了基于行为的编队方法，通过局部感知及较少的通讯信息使得机器人建立并保持相对的位姿关系实现编队。文献[3]将机器人视为虚拟刚性结构上的点，实现了基于虚拟结构的编队控制。文献[4]将虚拟结构法与路径跟踪法相结合，实现了多个机器人的队形控制。文献[5]将队形控制问题转化为机器人对于虚拟机器人的跟踪，但是算法实现要保证内三角关系，不适用于线形等特殊队形。针对机器人的路径跟踪问题，文献[6]采用模糊控制方法使两轮差动机器人跟踪给定路径。文献[7]采用反步法设计差动两轮机器人轨迹跟踪控制器，实现路径有效跟踪。文献[8]针对全向移动机器人轨迹跟踪任务，提出一种鲁棒轨迹跟踪控制方法，减小在控制过程中的扰动。

本文针对全向机器人的运动学特点，结合文献[5]，提出新的编队方法。领航机器人指引运动方向，生成虚拟机器人，构造跟踪误差系统，采用BackStepping方法设计控制器，实现全向机器人的编队控制。最后，仿真和实物实验验证了所提方法的有效性。

1 机器人的运动学模型

全向机器人如图1所示，装有4个万向轮作为驱动轮，间隔90°均匀分布，由四路电机控制机器人的运动。为便于分析机器人运动学特性，做以下假设：不考虑地面起伏且全向机器人的驱动轮不打滑；机器人的重心在其几何中心上；全向机器人视作刚体，不考虑形变问题。

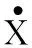
图1 全向机器人实物图

图2 全向机器人数学模型

坐标系的平移和旋转矩阵为

(1)

(2)

机器人的运动学模型方程为

(3)

(4)

(5)

中心点速度矩阵与4个驱动轮的角速度之间的关系为

(6)

(7)

式(6)中，r为驱动轮的半径，Wω=[ω1ω2ω3ω4]T为四个轮子的角速度。具体的公式见式(8)：

(8)

2 领导-跟随方法

由Rr的位姿可以得到Rv的位姿为：

(9)

(10)

跟踪误差的运动学方程为：

(11)

图3 领导跟随方法三角形编队结构

3 基于反步法的控制器设计

Backstepping方法是将非线性系统分解成不超过系统阶数的子系统，然后为每个子系统分别设计李雅普诺夫函数和中间虚拟控制量，通过后推，逐步修正算法[9]，将它们集成起来完成系统的控制器设计。本文第二节将多机器人的编队问题转化为跟随者的轨迹跟踪问题，因此在本节介绍轨迹跟踪控制器的设计。

引理1：对于任意x∈R，|x|<∞，有φ(x)=xsin(arctanx)≥0，当且仅当x=0时等号成立。具体证明过程见文献[10]。

本文将轨迹跟踪误差中的xe视为轨迹跟踪的虚拟控制量，引入特定的虚拟反馈变量：

(12)

(13)

由式(13)可以看出，当e3趋向零，e1趋向于sin(arctanω)e2时，使得e2同时收敛到零。

进一步选取全局李雅普诺夫函数，通过设计合适的控制律使得李雅普诺夫函数负定，系统达到稳定状态。

(14)

(15)

由式(12)可以得到

(16)

将式(16)、式(11)代入式(15)，得。

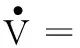
(18)

设计系统控制律为：

(19)

其中，式(19)满足k1>0，k2>0。

当速度和角速度满足式(19)的控制律，可得

(20)

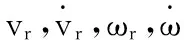
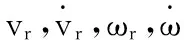
4 实验验证

4.1 仿真实验

4.1.1 直线编队实验

图4 三角形编队轨迹效果图

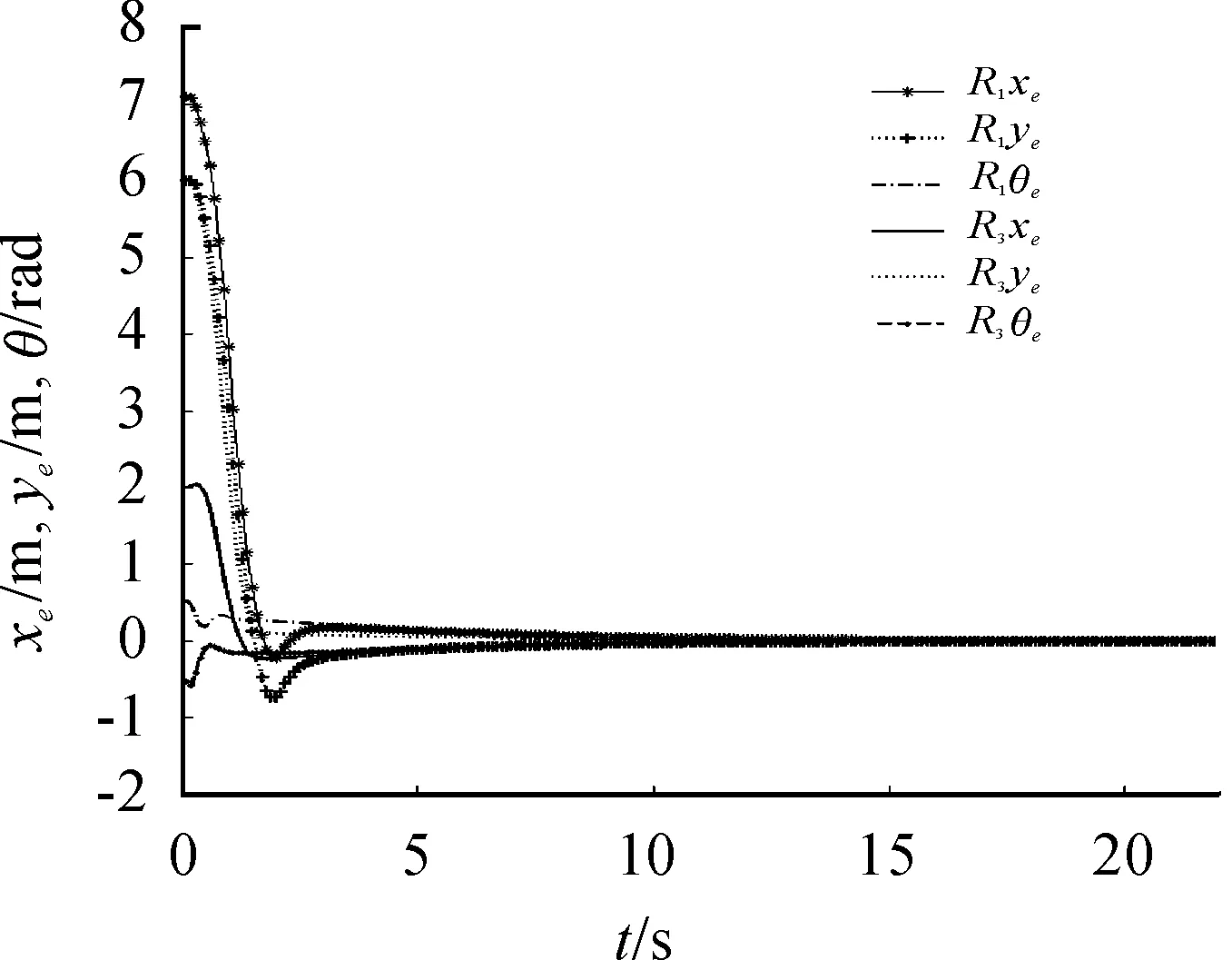
图5 R1R3跟踪误差

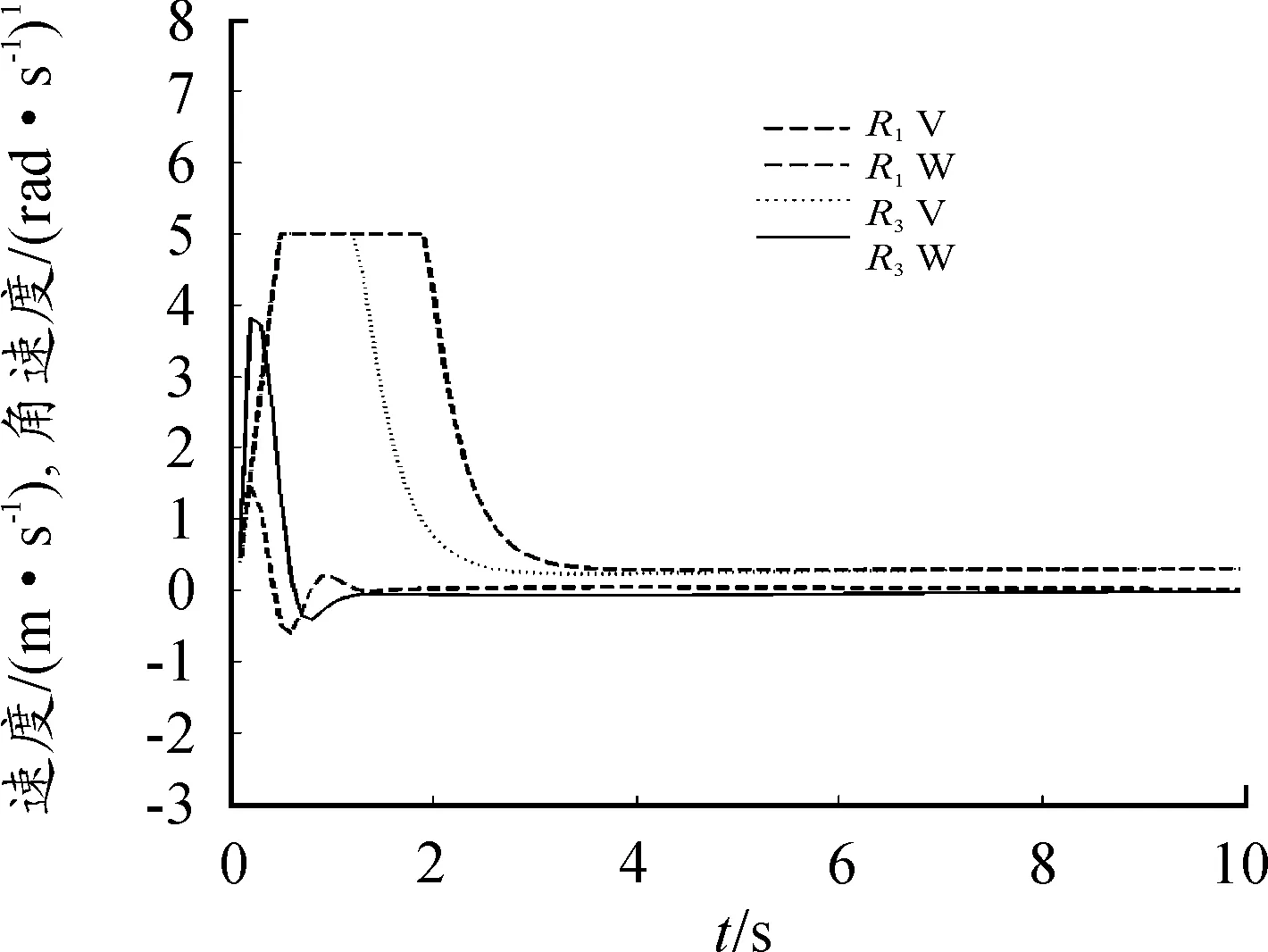
图6 机器人速度角速度曲线

4.1.2 圆编队实验

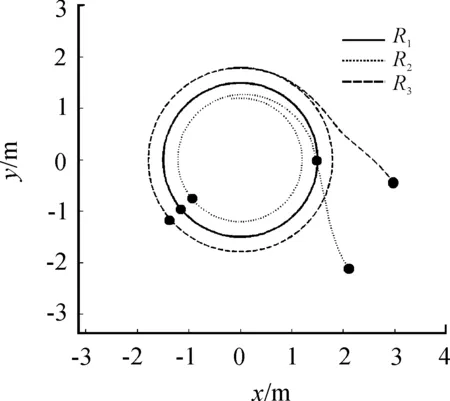
图7 同心圆编队轨迹效果图

图8 R2R3跟踪误差

4.2 实物实验

从实际应用的角度出发，进一步证明编队方法的有效性，采用多机器人协同系统进行实物实验。

实验采用的实验室自行研制的全向移动机器人平台，如图10所示，系统由3台相同的全向机器人组成，基于WIFI技术通信，通过UWB 定位系统获取机器人的实时位姿信息。控制系统由上位机和下位机组成，上位机基于VC开发，主要用于接收无线通信信息、障碍物距离信息、位置信息，并实时计算得到智能体的运动控制信息。下位机主控制器为TI公司的TMS320F28069作为主控制芯片，主要用于收集速度和电流信息，并根据上位机下发的控制指令控制机器人的电机转速，从而控制机器人的位姿和速度。在上位机上通过UWB定位系统记录机器人的位置坐标，将获得的数据进行处理，获得机器人的运行轨迹图。

图9 机器人速度角速度曲线

图10 多机器人系统实物图

实验中，机器人沿着正弦曲线做编队运动。图11为UWB定位系统得到的机器人的实时轨迹图。其中R2为领航机器人，R1和R3均为跟随机器人。“××”表示机器人的实际位置，R2轨迹中的正弦实线为机器人的期望曲线，R1轨迹中的实线和R3的实线分别表示机器人实际运动轨迹的拟合曲线。

图11 机器人编队轨迹

从编队轨迹图11可以看出，实验中R1和R3机器人能够跟踪领航机器人R2做类正弦曲线编队运动，证明了本文提出的编队方法的有效性。但是由于实验场地摩擦力、地面起伏和通信延迟等因素的影响，导致机器人运动过程中的存在扰动和跟踪误差，形成的正弦追踪曲线并不非常光滑。

5 结论

本文对全向移动机器人编队控制问题进行研究，提出了一种基于Backstepping的编队控制方法。通过仿真和实物实验可知机器人能迅速形成编队，并以较小的误差保持队形做编队运动，验证了本文所提出的编队控制律的有效性。下一步还需要研究多机器人系统在外界因素干扰的情况下如何保持编队性能的稳定。

[1] 张汝波,王兢,孙世良.具有环境自适应能力的多机器人编队系统研究[J].机器人,2004,26(1):29-73.

[2] FREDSLUND J,MATARIC M J.A general algorithm for robot formations using local sensing and minimal communication[J].IEEE Transactions on Robotics and Automation,2002,18(5):837-846.

[3] WEI R,SORENSEN N.Distributed coordination architecture for multi-robot formation control[J].Robotics and Autonomous Systems,2010,58(5):727-736.

[4] LEWIS M A,TAN K H.High precision formation control of mobile robots using virtual structures[J].Autonomous Robots,1997,4(4):387-403.

[5] 王保防,张瑞雷,李胜,等.基于轨迹跟踪车式移动机器人编队控制[J].控制与决策,2015,30(1):176-180.

[6] 吴垠,刘忠信,陈增强,等.一种基于模糊方法的领导跟随型多机器人编队控制[J].智能系统学报，2015,10(4):533-540.

[7] 李会来,李小民,陈静华.非完整移动机器人轨迹跟踪自适应控制器设计[J].传感器与微系统，2013,30(5):104-108.

[8] 杨俊友,白殿春,王硕玉.方位轮式下肢康复训练机器人轨迹跟踪控制[J].机器人,2011,33(3):915-318.

[9] 付明玉,王奎民,边信黔,等.模糊-反步串级控制方法在气垫船航迹保持中的应用[J].中国造船，2009,20(1):83-P91.

[10]徐俊艳,张培仁.非完整轮式移动机器人轨迹跟踪控制研究[J].中国科学技术大学学报,2004,34(3):376-380.

[11]吴卫国,陈辉堂,王月娟.机器人的全局轨迹跟踪控制[J].机器人，2001,27(3)：327-330.

(责任编辑 杨继森)

Formation Control of Omnidirectional Robot Based on Backstepping

WANG Qinzhao, CHENG Jinyong, Li Xiaolong

(Academy of Armored Force Engineering, Beijing 100072, China)

A multi-robot coordinated formation algorithm is proposed. Virtual robot is established according to the leader’s pose and the desired formation parameters. The formation problem based on leader follower algorithm is transformed into robot trajectory tracking problems following the virtual leader. We uses BackStepping method to construct Lyapunov function, making the function negative-definite. The formation controller is realized in this way. Simulation and experiment results show that the proposed controller is effective.

omnidirectional robot; BackStepping; formation; trajectory tracking

2017-03-22；

2017-04-26

王钦钊(1973—)，男，教授，博士生导师，主要从事系统仿真、导航制导与控制研究。

10.11809/scbgxb2017.08.022

format:WANG Qinzhao, CHENG Jinyong, Li Xiaolong.Formation Control of Omnidirectional Robot Based on Backstepping[J].Journal of Ordnance Equipment Engineering,2017(8):98-102.

TP391

A

2096-2304(2017)08-0098-05

本文引用格式：王钦钊，程金勇，李小龙.基于BackStepping的全向机器人编队控制[J].兵器装备工程学报，2017(8):98-102.