助飞反潜鱼雷落点精度的Bayes评估方法

邢国强，翟东民

(中国人民解放军91439部队， 辽宁 大连 116041)

【装备理论与装备技术】

助飞反潜鱼雷落点精度的Bayes评估方法

邢国强，翟东民

(中国人民解放军91439部队， 辽宁 大连 116041)

针对助飞反潜鱼雷落点精度指标特点(采用标准方差σ表示)以及评估该指标过程中遇到的本舰定位误差过大的实际问题，提出对该指标采用验前信息的二项分布Bayes假设检验方法进行综合评定；采用数据预处理方法将舰位定位偏差分离。算例表明：该方法能有效利用试验数据，对助飞反潜鱼雷落点精度指标进行科学充分的评定和估算。

助飞反潜鱼雷;落点精度;Bayes方法;定位误差

助飞反潜鱼雷落点精度是考核其作战效能的重要指标之一，直接决定作战效能大小,其指标常采用标准方差(σ)表示，主要由初始误差[1]、助飞反潜鱼雷制导误差以及空中各种分离误差等3种误差构成。初始误差为本舰定位误差，可借鉴导弹落点精度评定方法[2-3]确定。在现场试验次数较少、样本数较少或特小子样情况下,采用经典统计方法对落点精度进行评定会有很大的风险。一般采用验前信息的二项分布Bayes假设检验综合评定方法[4-7]，本文采用此方法对助飞反潜鱼雷落点精度指标进行评定。在实际评定落点精度指标时，由于现场试验，有若干条次的本舰舰位偏差超过了规定的本舰定位误差，不符合落点精度的评定要求，若将这些试验条次评定为无效条次，现场试验样本量本来就不充分，将造成试验样本量更少，无法真正科学充分评定助飞反潜鱼雷的落点精度指标。

针对此问题，为充分利用现场试验样本量，本文使用数据预计算处理方法，对所有参与评定落点偏差的数据进行不含舰位偏差的数据处理，然后加上规定的本舰定位误差指标，对落点精度进行Bayes综合评定和估算。

1 评估方法

1.1 评估落点精度的总体思路

将助飞反潜鱼雷落点精度转换为二项分布成败型问题中的参数估计问题，用Bayes假设检验方法评估二项分布参数的属性，根据验前信息计算验前概率，由试验现场的试验条次数确定判决门限和评定方案，作出落点精度是否满足指标的判定，并给出落点精度的估计值。

但助飞反潜鱼雷落点精度指标采用标准方差(σ)表示，文献[1]中提出也可用标准方差(σ)替代圆概率误差(CEP)，进行二项分布Bayes假设检验。为估算该指标值，首先计算出圆概率偏差( CEP)，然后利用标准方差与圆概率偏差转换关系，反求出标准方差(σ)的估计值。

对于因舰位偏差过大所获取的落点偏差，采用数据预处理方法，对所有参与评定落点偏差的数据进行不含舰位偏差的数据处理，计算出不含舰位偏差的标准方差(σ雷)，然后再加上规定的舰位偏差的标准方差(σ舰)，求出标准方差(σ)的估计值，作为落点精度指标的估计值。

1.2 二项分布Bayes假设检验评定方法

1.2.1 评定方法

考虑以下假设检验问题：

(1)

其中λ>1为鉴别比。

假定得到验前信息X={x1,x2,…,xn0}，设落入以ησ0(η>0)为半径的圆内的验前落点个数记为m0，并取m0为统计量，令

(2)

(3)

其中P(H0)、P(H1)为无信息验前概率，一般根据同等无知原则取为0.5，π0和π1的计算见文献[3]。

如果在现场试验中，在n个样本中，共有m个条次落入以ησ0为半径的圆内，则

(4)

(5)

当m>S时，接收原假设H0，即认为鱼雷入水点精度满足指标要求；否则，接收备择假设H1。

1.2.2 双方风险计算

假定在n条次鱼雷试验中，有m条落入目标区域。如果判决门限为S，可以计算出研制方和使用方的风险，分别见式(6)和式(7)。

(6)

(7)

其中[·]表示取整数部分。

1.2.3 评定准则

在落点精度评定的假设检验过程中，落入圆半径以及鉴别比的确定伸缩性较大，它直接决定研制方和使用方风险[8]。根据仿真计算结果，如果依据双方风险相当的原则确定试验方案，则落入圆半径越大，所需样本量越多。考虑现场试验时可供使用的试验样本量，在双方风险基本相当的原则下，选取落入圆半径ησ0，基于同样的原因并兼顾试验的可实施性，选定鉴别比λ，由此可确定评定准则如下：

在双方风险约定在某值条件下，在n个样本中，共有m个条次落入以ησ0为半径的圆内，则判落点精度指标合格，否则不合格。

1.3 落点精度评估值

1.3.1 数据预处理

1) 地理坐标系下的舰位偏差计算。由GPS外测设备提供本舰发射时刻的经纬度坐标，即Os(N,E)；由外测设备提供的发射时刻鱼雷的惯导经纬度坐标，即Oj(N,E)；求出OjOs的距离和方位：ΔR0，α0，如图1所示。

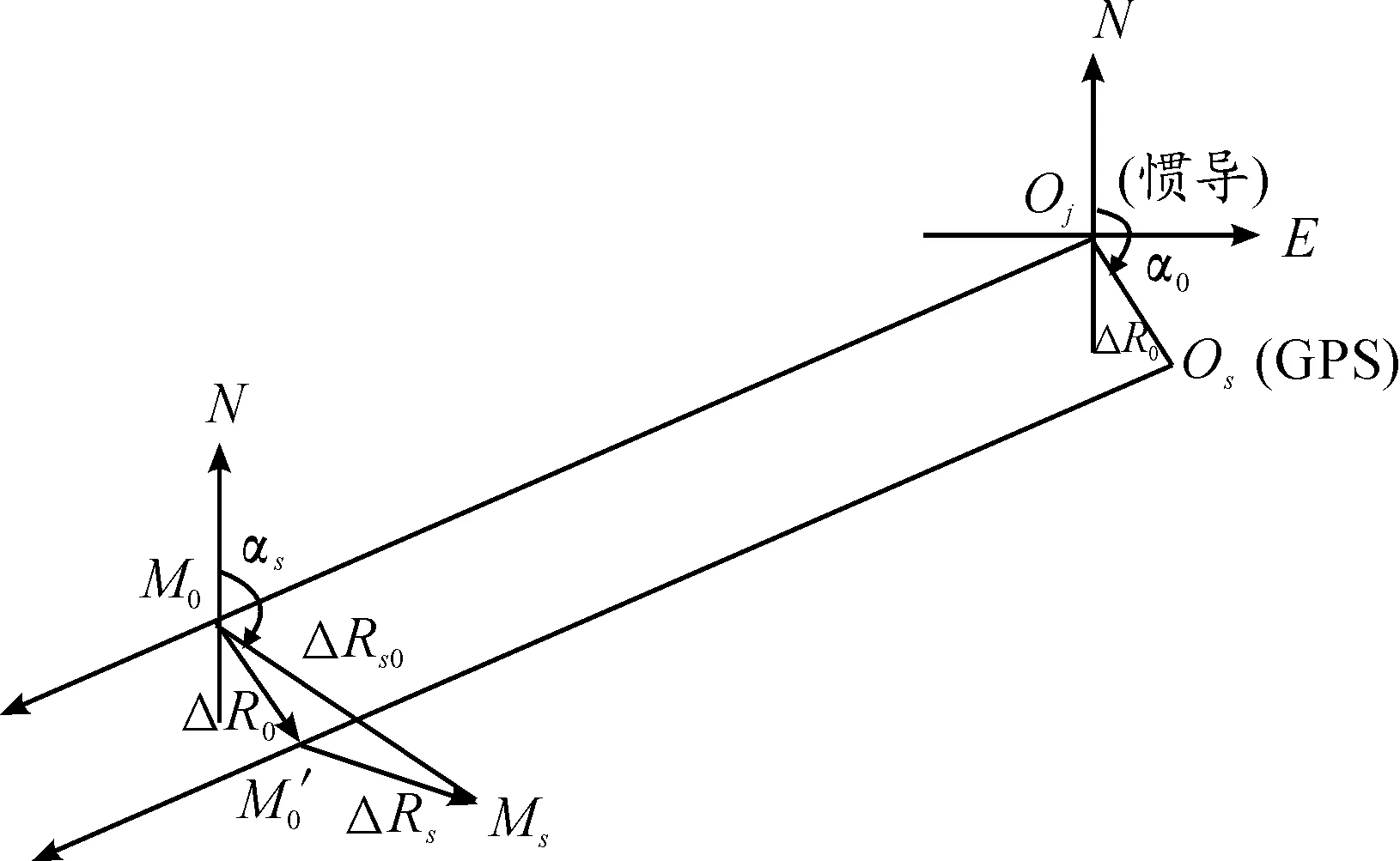
图1 偏差示意图

2) 建立发射坐标系。建立以实际发射点Os(GPS)为原点，以指向落点M0为纵轴Xn的发射坐标系OsXnZn，已知Os(N,E) 和M0(N,E)，可得到坐标轴OsXn与北夹角α0(目标方位角)，如图2中坐标系OsXnZn。

图2 发射坐标系

3) 发射坐标系下的偏差计算。假设某偏差的大小为ΔR，在地理坐标系中方位角为α，所选坐标系目标方位角为α0，则偏差在发射坐标系中分量如图3所示。

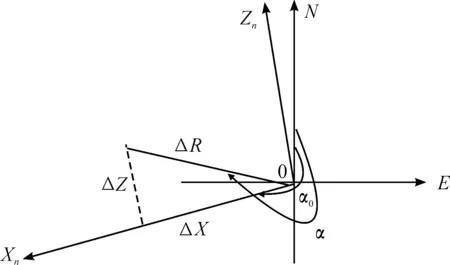
图3 偏差及分量

根据图3，偏差ΔR在所选定的坐标系中的分量计算公式如下：

(8)

按照式(7)，可得本舰舰位偏差分量的计算公式如下：

(9)

由此获得不含本舰舰位偏差的计算公式如下：

(10)

1.3.2 圆概率偏差计算值

首先根据试验数据，解算圆概率误差(CEP)的估计值，然后计算标准方差σ的估计值。

根据定义，假设纵向落点偏差X和横向落点偏差Z均服从正态分布，且相互独立，(X,Z)的联合概率密度函数为

(11)

满足下式的R即为圆概率误差(CEP)：

(12)

设试验得到样本量为n的精度评定样本(x1,z1)，…，(xn,zn)，则样本均值和样本标准差的估计值为

(13)

(14)

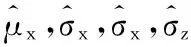
1.3.3 标准方差计算值

一般按无系统偏差且偏差独立同分布情况下[8]，或偏差呈弱相关，可认为偏差独立同分布[9-10]，可按式(17)计算不含舰位偏差的落点精度的估计值σ雷：

(17)

设规定的本舰定位误差值为σ舰，落点精度指标评估值σ：

(18)

2 算例分析

假设某型助飞反潜鱼雷验前信息3条次，落点偏差分别为330 m、350 m、823 m；现场试验信息8条次，落点偏差分别为300 m、451 m、380 m、790 m、1 280 m、243 m、1 162 m、355 m，已知落点精度指标(1σ)不大于500 m，现场试验第5和7条次数据中本舰舰位偏差超过规定的要求200 m(1σ)，分别为631 m和610 m，其余所有条次均满足本舰定位误差要求，试问该指标是否满足要求，并求其估计值。

试验前，制定评定方案，选取落入圆半径R=1.5σ0和R=2σ0，即η=1.5和η=2，基于同样的原因并兼顾试验的可实施性，分别选定鉴别比λ=1.2和λ=1.3，按式(2)、式(3)、式(4)计算验前概率，代入式(5)，并根据式(6)、式(7)计算双方风险，可得评定方案及双方风险，见表1和表2。

由表1和表2计算结果和双方风险值看，在基于双方约定的风险不大于0.25的情形下，当η=2和λ=1.3时，评定方案最为科学合理，因此可制定该雷落点精度指标评定方案为:现场试验时， 8个有效条次中不少于5条次落入半径R=2σ0的圆中，则判落点精度指标合格，否则不合格。

表1 η=1.5评定方案及对应的风险

表2 η=2评定方案及对应的风险

本算例中因为有两条次本舰定位误差超差，若判为无效项目，本来试验样本量就少，这对于科学充分评估落点精度指标不利，通过本文采用的数据预处理方法，即按照式(8)、式(9)、式(10)，将全部原始试验数据进行不含舰位偏差的计算，获得新的落点偏差，经处理后的验前信息3条次，落点偏差分别为450m、320m、623m；现场试验落点偏差分别为1 023m、400m、478m、393m、416m、1 177m、466m、400m。

依据该雷落点精度指标评定方案，现场试验落点偏差8条次试验数据中只有2条次超过1 000m的半径圆，可判落点精度指标合格。

将新落点偏差的X方向和Z方向数据，代入式(13)、式(14)、式(15)、式(16)，根据式(12)，可计算出不含舰位偏差的CEP，代入式(17)、式(18)中可得落点精度指标评估值σ为433m(σ舰=200m)。

3 结论

本文所采用的助飞反潜鱼雷落点精度的Bayes综合评定方法，已得到实际运用，可有效解决试验样本量较少、评定置信度不高的试验鉴定难题；尤其是针对本舰定位误差超过评定落点精度要求规定的指标时，为有效利用现场不易得到的试验数据，提供了新的解决方法，大大节省了试验经费和周期，且提高了评估精度。

[1] 张耐民,李赣湘,严佳民.误差分离技术及其在导弹精度分析中的应用[J].导弹与航天运载技术， 2005(6)：28-31.

[2] 程光显,张士峰.导弹落点精度的鉴定方法：概率圆方法[J].国防科技大学学报，2001(5)：13-16.

[3] 张士峰,夏胜平,贾沛然.导弹落点精度的综合评定方法[J].兵工学报,2002,23(2)：255-257.

[4] 邢国强,曲兆宇,冯殿震.考虑可信度的平均寿命验后分布Bayes融合评估方法[J].科学技术与工程,2012,12(9)：2183-2186.

[5] 许海昀,谢君红,高顺林.炸雷弹落点精度评定的假设检验方法[J].水雷战与舰船防护， 2014(3)：13-15.

[6] 张金槐,唐雪梅.Bayes方法[M].长沙：国防科技大学出版社， 1993.

[7] 张金槐,刘琦.Bayes试验分析方法[M].长沙：国防科技大学出版社，2007.

[8] 宋凯，夏晨秋，张承伟.弹丸落点被动声定位方法[J].兵工自动化，2015(6):1-4.

[9] 曲宝忠，孙晓峰.海军战术导弹试验与鉴定[M].北京：国防工业出版社，2005.

[10]孙伟,金振中,单时卓.某型导弹落点精度评定方法[J].战术导弹技术， 2004(6)：29-31.

[11]高善清,邢立新,樊海刚.炮射导弹落点精度评定[J].弹箭与制导学报，2008，28(1)：203-205.

(责任编辑 周江川)

Accuracy Assessment Bayesian Method of Fall Points for Assisted Antisubmarine Torpedo

XING Guoqiang, ZHAI Dongmin

(The No. 91439thTroop of PLA, Dalian 116041, China)

According to the characteristics of the falling point precision index of assisted antisubmarine torpedo(the standard abbreviation often used ), as well as the practical problems encountered in the evaluation of the target positioning error are too large. The binomial distribution Bayes hypothesis test method is used to evaluate the index; Aiming at the large ship positioning error, the method of data prepossessing is used to separate the position location deviation; The experimental results show that the method can achieve the effective use of test data and make a scientific evaluation and estimation of the target value.

assisted antisubmarine torpedo; accuracy of fall point; Bayes method; positioning error

2017-03-12；

2017-04-10

邢国强(1970—)，男，高级工程师，主要从事鱼雷试验总体研究。

10.11809/scbgxb2017.08.006

format:XING Guoqiang, ZHAI Dongmin.Accuracy Assessment Bayesian Method of Fall Points for Assisted Antisubmarine Torpedo[J].Journal of Ordnance Equipment Engineering,2017(8):21-24.

TJ63

A

2096-2304(2017)08-0021-04

本文引用格式：邢国强，翟东民.助飞反潜鱼雷落点精度的Bayes评估方法[J].兵器装备工程学报，2017(8):21-24.