钨球对柱面带壳装药的冲击起爆数值模拟研究

王昕， 蒋建伟， 王树有， 李梅

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

钨球对柱面带壳装药的冲击起爆数值模拟研究

王昕， 蒋建伟， 王树有， 李梅

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

采用AUTODYN-3D数值软件，开展了钨球与不同曲率半径柱面带钢壳Comp B炸药作用过程的数值模拟。分析了钨球撞击位置对炸药冲击起爆特性的影响，采用升降法获得柱面带壳装药的临界冲击起爆速度。结果表明：柱面带壳装药冲击起爆过程与平面带壳装药相一致，炸药起爆点发生在离炸药和壳体界面一定距离处，且随着速增加而越靠近交界面；相同条件下柱壳装药更易于起爆，其临界起爆速度随装药曲率半径r增加呈现非线性增大，碰撞点偏移量δ=0时，r=∞的临界起爆速度较r=40 mm时增加3.2%；随偏移量δ的增大呈现指数增加，r=40 mm时，δ=0.94r的临界起爆速度较δ=0时增加35.6%，较平面带壳装药增加31.5%.

兵器科学与技术； 柱面带壳装药； 起爆点； 临界起爆速度

0 引言

对来袭弹药进行有效拦截毁伤是当今弹药技术研究的热点问题[1]。采用破片对其战斗部高速侵彻实施引爆是最有效的手段，而问题的实质则是破片对带壳装药的冲击起爆。

国内外学者针对这一问题已进行了广泛的研究。从公布的文献上来看，大多以破片冲击平面带壳装药模型为基础，主要采用理论、数值模拟和试验方法开展研究。包括不同材质、形状破片[2-5]对不同厚度壳体、炸药[6]的冲击起爆及起爆判据的建立[7-13]。然而，实际战斗部多为圆柱形结构，平面带壳装药的冲击起爆判据能否适用尚待验证。一些学者也曾开展了相关试验和数值模拟分析，其中宋浦等[14]开展某型破片式战斗部对柱壳装药的撞击毁伤试验研究，得到柱壳装药引燃、引爆的阈值范围；辛建国等[15]等通过破片冲击柱面薄壳装药试验，得到壳体和破片的机械作用是引爆薄壳装药的主要原因；江增荣等[1]则开展破片材料对冲击起爆影响的数值模拟研究，提出重金属破片可提高反导战斗部毁伤能力。但这些研究并未给出柱面带壳装药和平面带壳装药在起爆机理及起爆判据上的差异。

本文采用AUTODYN-3D数值软件针对钨球冲击起爆柱面带壳装药(简称柱壳装药)问题进行数值模拟。通过分析钨球以不同着速命中装药不同位置的冲击起爆过程，揭示柱壳装药冲击起爆机理，得到各参数对炸药冲击起爆阈值的影响规律。研究结果可为工程应用提供参考。

1 数值模拟模型

1.1 物理模型

图1为钨球与柱壳装药作用的物理模型。其中钨球质量m；带壳装药中炸药曲率半径r、长度l，材料为Comp B炸药；壳体厚度h，材料为钢。为了简化计算，假设钨球垂直于带壳装药轴线入射。

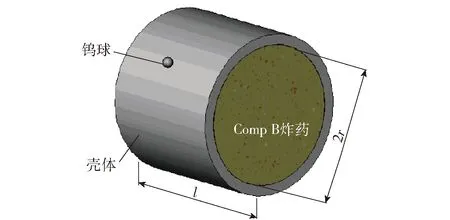
图1 钨球与柱壳装药作用物理模型图Fig.1 Physical model of tungsten fragment impacting on cylindrical charge with steel casing

图2为钨球碰撞点剖面示意及参数定义图。其中O1、O2分别为带壳装药轴心和钨球中心；钨球以着速v撞击柱壳装药不同位置，定义碰撞点相对于O1的垂直距离为碰撞点偏移量，记为δ；O1O2与v夹角为撞击角，记为θ，由几何关系可得sinθ=δ/(r+h)；碰撞点处的壳体水平厚度记为hθ，即hθ=h/cosθ;沿碰撞点法线与切线方向将着速分解为垂直速度vv和滑移速度vs;在θ为0～75°范围内沿装药半径方向每间隔7.5°设置一列观测点，列号设为θ_1～θ_11，每列观测点间间距4 mm.

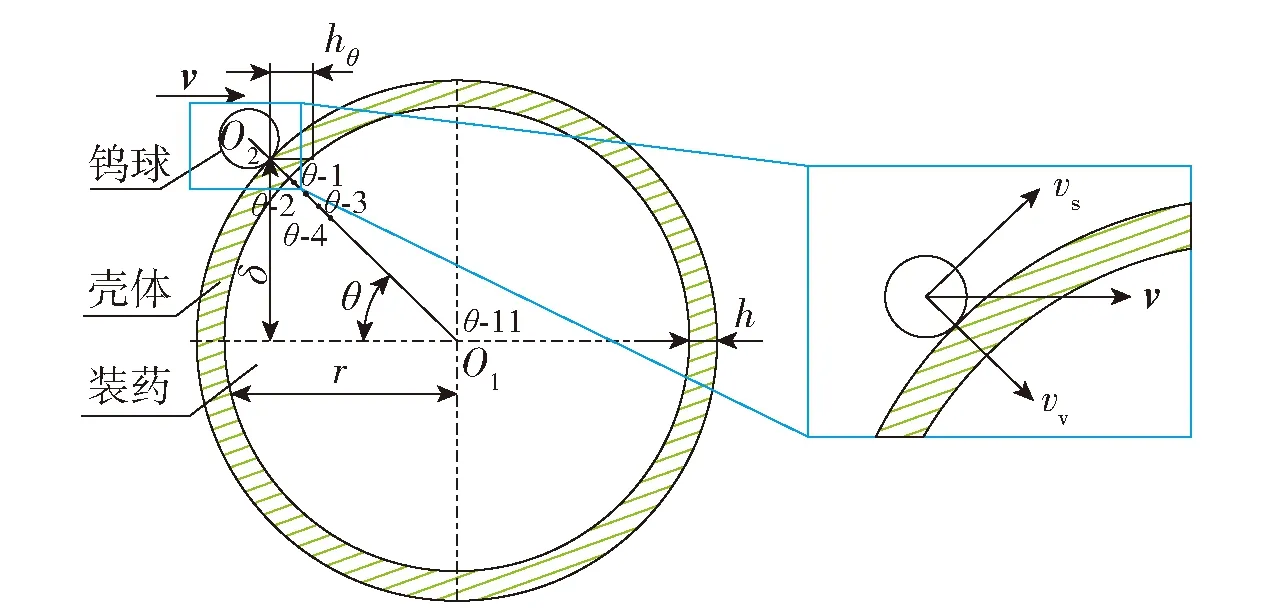
图2 钨球碰撞点剖面示意及参数定义图Fig.2 Impact point and parameter definition

1.2 数值模拟模型

采用AUTODYN-3D数值软件建立离散化模型。考虑模型对称性，建立1/2模型以简化计算。图3为建立的钨球、壳体和炸药的离散化网格模型，网格数量分别为2 048、2 880、192 000，采用Lagrange方法开展计算。

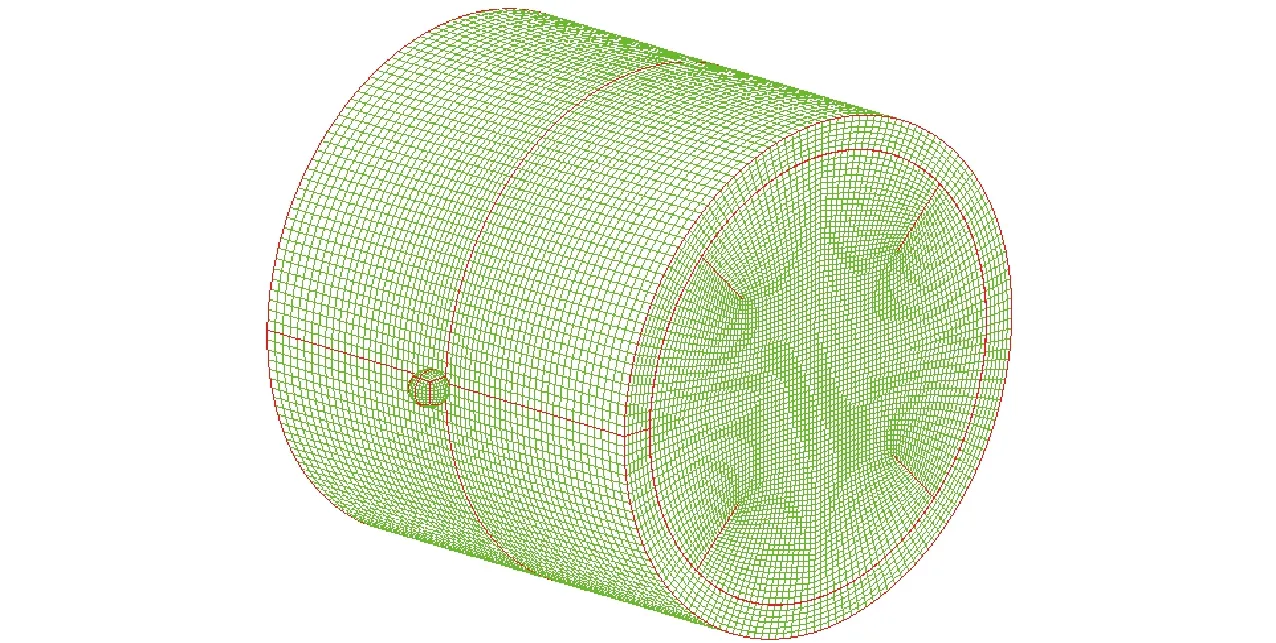
图3 离散化网格模型Fig.3 Discrete model

为了描述炸药在冲击作用下的起爆过程，其状态方程采用Lee-Tarver状态方程[16]：

dF/dt=I(1-F)b(μ-a)x+
G1(1-F)cFdpy+G2(1-F)eFgpz,

(1)

式中：F为燃烧质量分数，它在模拟爆轰过程中控制炸药化学能的释放；参数I和x为点火量冲击强度及持续函数；μ为炸药压缩比；a为临界压缩度参数；b为点火项燃耗阶数；参数G1和d为控制点火后早期增长函数；c、y为燃烧项的燃耗阶数和压力幂数；参数G2和z为高压反映率相关函数；e、g为常数；p为爆炸气体压力。炸药未反应物和反应物均采用JWL状态方程。Comp B炸药模型参数取自AUTODYN材料库，具体参数见表1.

表1 Comp B炸药模型参数[17]

钨球和壳体选用能较好描述材料大应变、高应变率及高温度状态的Johnson-Cook强度模型，材料强度模型、状态方程和侵蚀准则列于表2中。参数取自AUTODYN标准数据库。

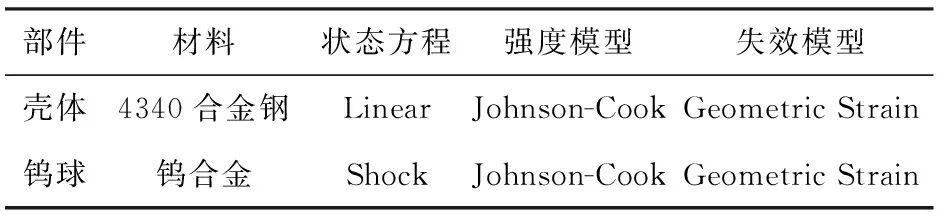
表2 钨球、壳体材料模型

1.3 计算工况

为了研究钨球对柱壳装药的冲击起爆过程，确定命中位置、装药曲率半径等参数对柱壳装药冲击起爆的影响，设计了表3所示的计算工况，其中m为参考典型预制破片战斗部中钨球的质量设定，依据常规弹药战斗部选取柱壳装药壳体厚度h和装药曲率半径r，碰撞点偏移量δ则根据撞击角θ分别为0°、15°、30°、45°、55°时的偏移距离制定。

采用“升降法”得到炸药临界起爆速度阈值，对比各工况炸药起爆点位置、观测点压力变化，阐明柱壳装药与平面带壳装药冲击起爆的差异。

1.4 模型校验

材料参数的正确与否与计算结果正确性直接相关。采用经典的皮克汀尼工程判据[9]对已建立的仿真模型进行验证，表4为针对工况2～工况5选取两种质量钨球撞击起爆的临界速度仿真值与理论值的对比。从表4可看出，仿真值与理论值误差约5%，即认定仿真算法的正确性。

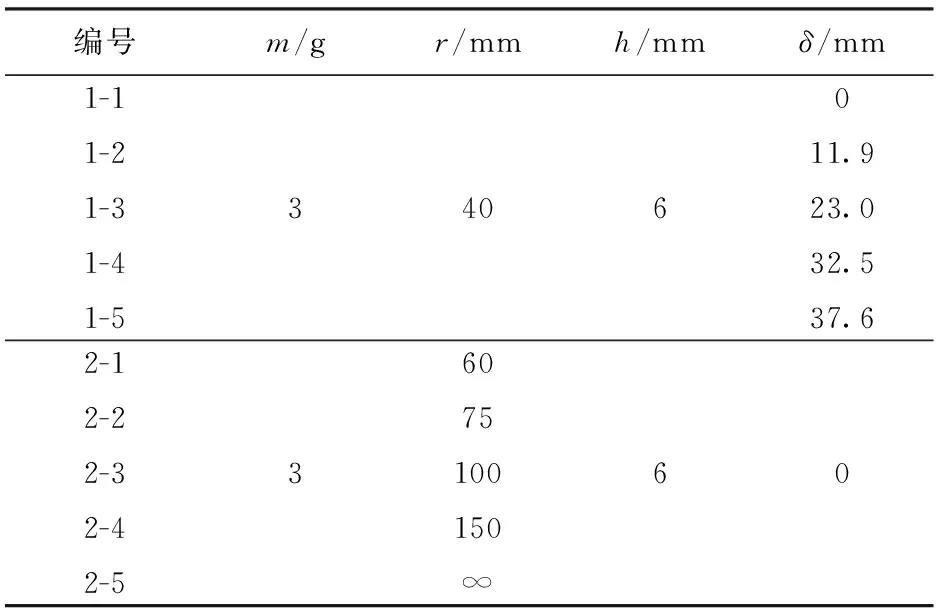
表3 计算工况列表

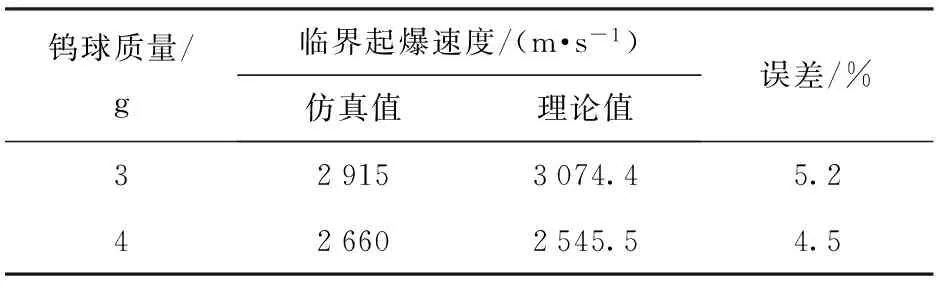
表4 临界起爆速度的仿真值与理论值对比

2 柱壳装药冲击起爆过程

选取钨球以碰撞点偏移量δ=0 mm对柱壳装药的冲击起爆过程进行详细说明。图4(a)与图4(b)、图4(c)与图4(d)分别为钨球在两种速度条件下撞击柱壳装药和平面带壳装药典型时刻应力图，图5为观测点压力随时间变化曲线。

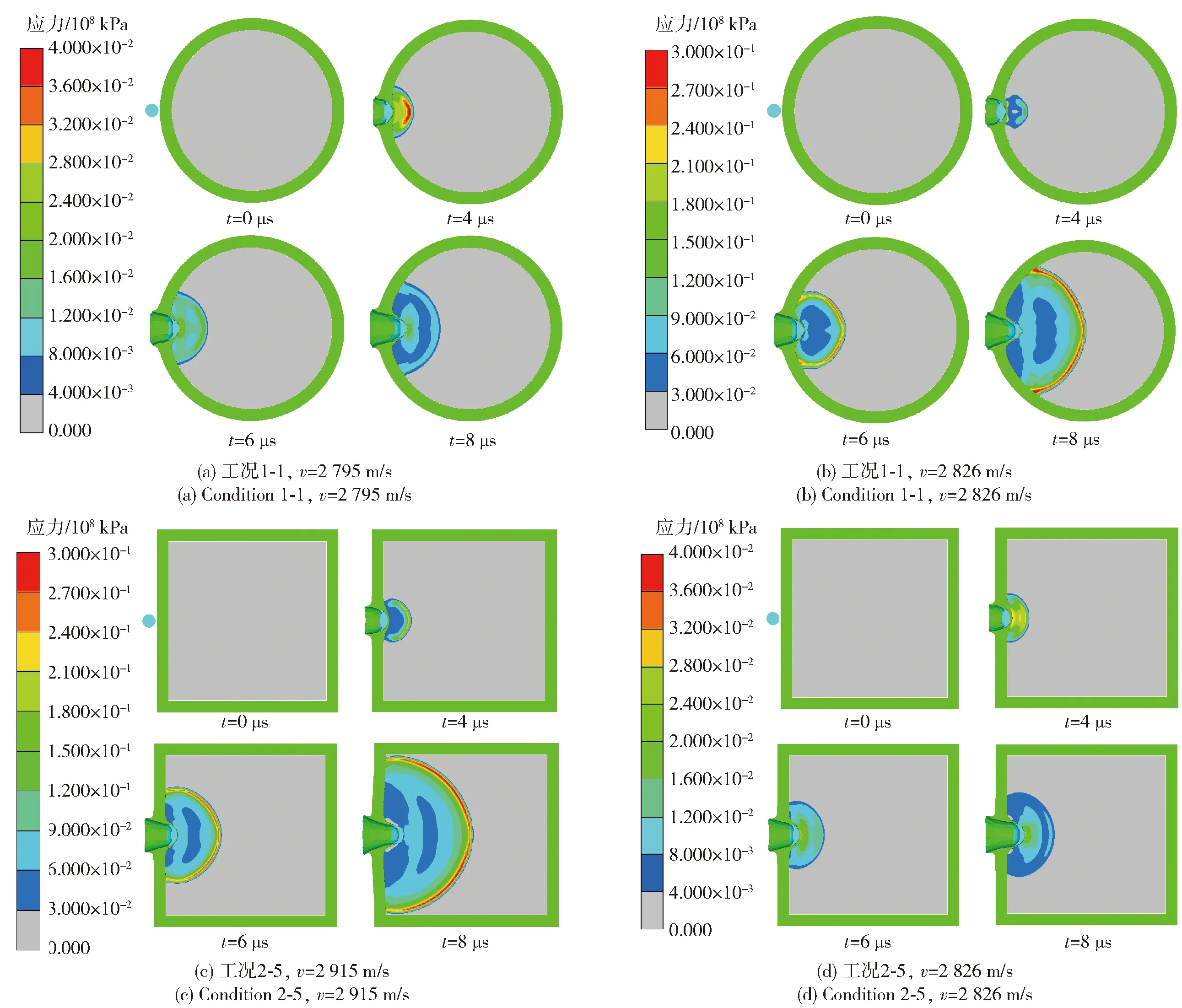
图4 钨球撞击柱形和平面带壳装药典型时刻应力图Fig.4 Typical time-stress diagram of tungsten fragments impacting cylindrical and plate charges

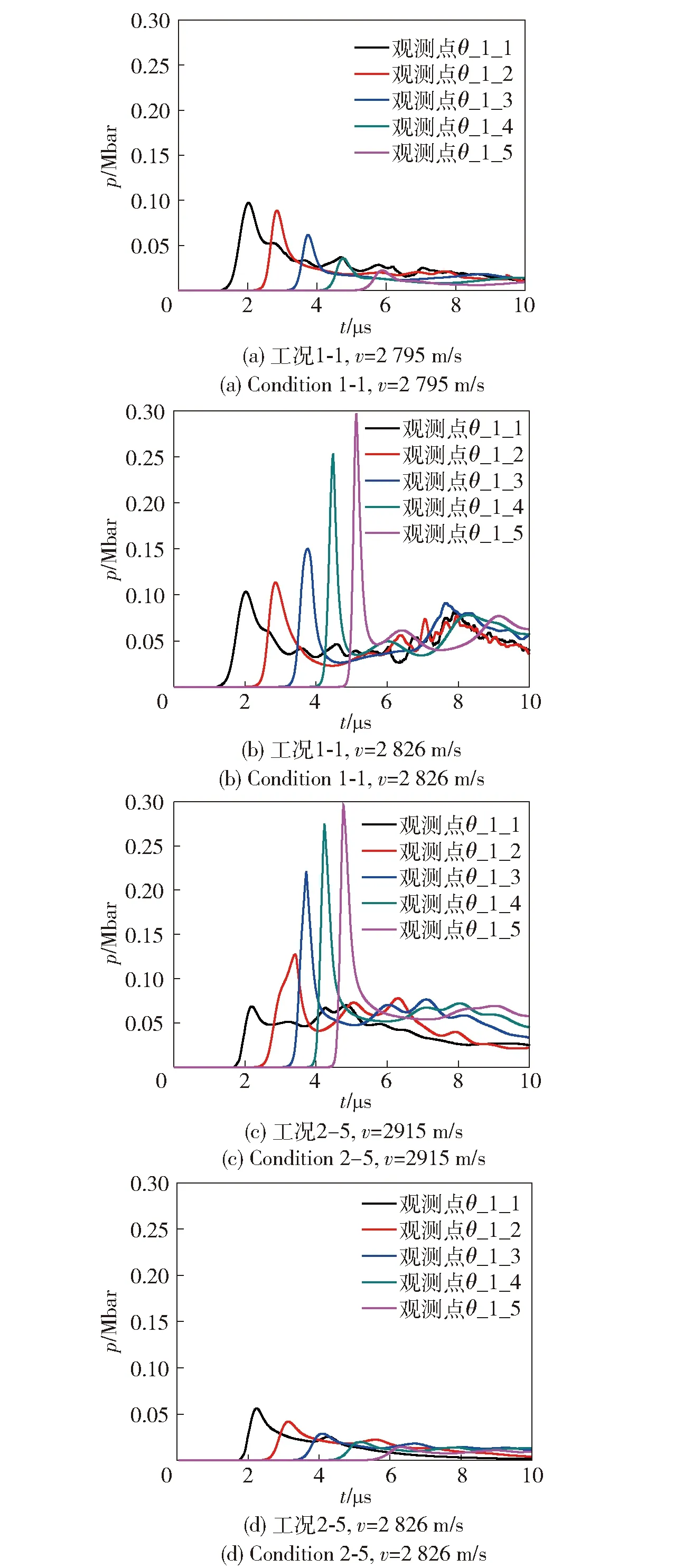
图5 炸药内观测点压力- 时间曲线Fig.5 Pressure-time curves of guages in charge

对于平面带壳装药的冲击起爆，在破片质量和速度一定时，这类冲击引爆机制与壳体厚薄程度有关。通常认为当壳体较薄时是冲击起爆机制，而当壳体较厚时是冲击起爆和剪切起爆两种机制并存[18]。考虑到本文研究的壳体厚度，以冲击起爆机制作为引爆机理开展研究。

从图4(a)、图4(b)可以看出，在4 μs时刻内，钨球作用过程表现为对钢壳的穿透和对装药的侵彻。v=2 826 m/s时，4 μs时刻距离壳体一定位置的炸药处出现应力阶跃点，并迅速向外传播，8 μs后形成稳定传播的爆轰波。而v=2 795 m/s时，冲击波随传播距离逐渐衰减，炸药未发生爆轰。对比图4(b)、图4(c)可以得到，柱壳和平面带壳装药冲击起爆过程基本一致，可确定柱壳装药的引爆机理同样为冲击起爆机制。

从图5的观测点压力- 时间曲线可得到相同结论。由图5(a)、图5(b)可看出：在v=2 826 m/s条件下0～3 μs时间内，第1列观测点θ_1_1、观测点θ_1_2变化趋势及压力值基本相同，在4 μs时刻观测点θ_1_3压力突然升高，随后压力继续上升至一定峰值并稳定传播。此压力的传播即为爆轰的传播，可确定起爆点在观测点θ_1_3和观测点θ_1_4附近。由于着速降低，图5(a)中观测点压力逐渐降低，表明炸药未发生稳定爆轰。对比图5(b)、图5(d)可看出，v=2 826 m/s时平面带壳装药内观测点压力逐渐减小，炸药未起爆。

图6为不同着速下柱壳装药第1列观测点压力- 时间曲线。从图6(a)中可看出，炸药起爆点在观测点θ_1_2和观测点θ_1_3附近，图6(b)显示起爆点在观测点θ_1_1和观测点θ_1_2附近。与图5(b)进行对比，可得炸药完全起爆时，起爆点随着速增加逐渐向炸药与壳体交界面靠近。

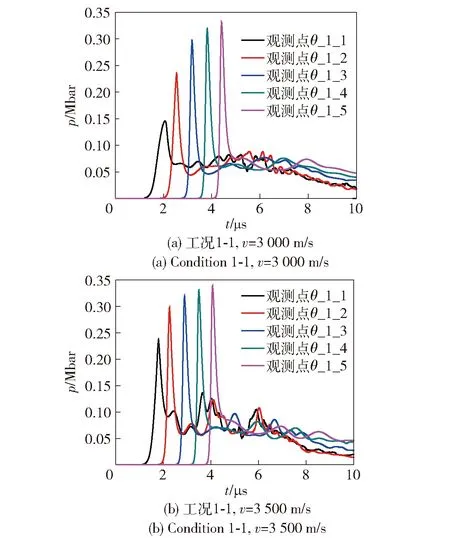
图6 不同着速下炸药内观测点压力- 时间曲线Fig.6 Pressure-time curves of guages at different impact velocities

上述仿真结果可得：

1)柱壳装药和平面带壳装药的冲击起爆过程基本一致；

2)起爆点离装药和壳体交界面一定距离，随着速增加，起爆点位置越靠近交界面。

3 柱壳装药的冲击起爆影响因素分析

3.1 钨球命中位置对柱壳装药冲击起爆影响

3.1.1 命中位置对冲击起爆现象的影响

对于平面带壳装药，速度方向一定时，命中位置对撞击角度并无影响；而对于柱壳装药，命中点位置不同意味着撞击角的改变，冲击起爆现象也将发生变化。

图7为着速相同、命中壳体不同位置时典型时刻应力图。与图4(a)相比，初始冲击波形状随命中位置不同呈现非对称性，压力阶跃点偏离碰撞点法线。碰撞点偏移量δ越大，炸药起爆将越困难。

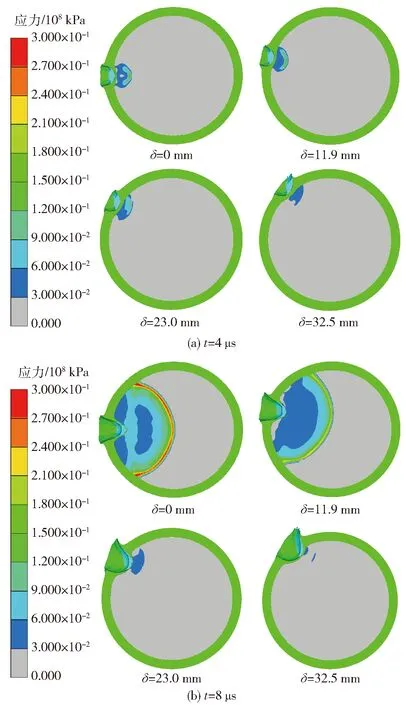
图7 v=2 920 m/s钨球命中不同位置时典型时刻炸药冲击起爆应力图Fig.7 Typical time-stress diagram of fragments impacting the different locations of cylindrical charge for v=2 920 m/s

3.1.2 命中位置对起爆点位置影响

提取计算文件中的观测点压力- 时间曲线以确定各工况炸药起爆点位置变化。图8为钨球以偏移量δ=11.9 mm(θ=15°)撞击柱壳装药时第2列、第3列、第4列观测点压力- 时间曲线。若起爆点位置位于第3列观测点上，则冲击波到达观测点θ_4_2和观测点θ_2_2的时间应相同。而图8显示冲击波观测点到达顺序为观测点θ_3_2、观测点θ_4_2、观测点θ_2_2，且观测点θ_4_2压力峰值高于观测点θ_2_2，由此可确定起爆点位于第3列至第4列观测点之间，即15°～22.5°之间。因此，撞击角存在时起爆点偏离O1O2连线，位于O1O2和v夹角并距离壳体与炸药界面一定距离。不同撞击角下的起爆点位置也具有类似特征。

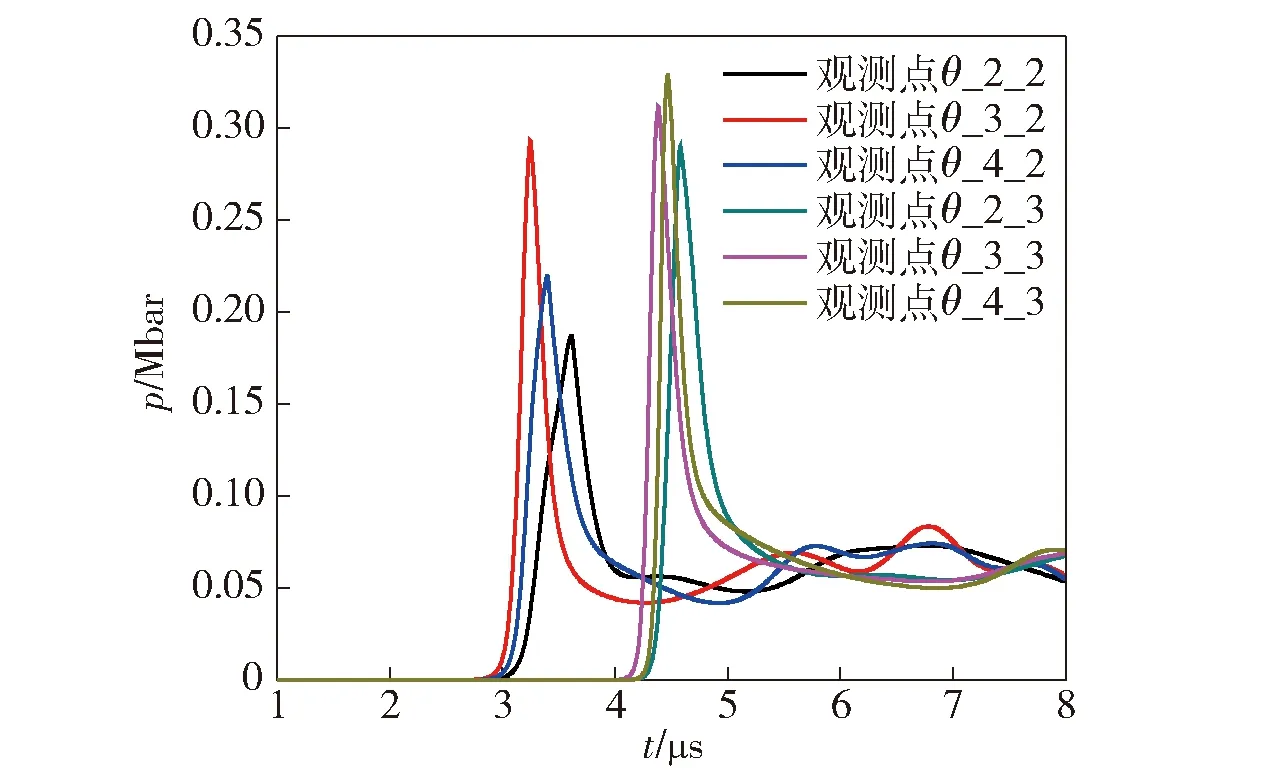
图8 v=2 920 m/s和δ=11.9 mm时炸药内观测点压力- 时间曲线Fig.8 Pressure-time curves of guages for v=2 920 m/s and δ=11.9 mm

3.1.3 命中位置对临界起爆速度的影响

通过“升降法”确定装药曲率半径r=40 mm、壳体厚度h=6 mm条件下炸药的临界起爆速度vc，以偏移量δ=0时的临界起爆速度vc0为基准作归一化处理。定义临界起爆速度增量Δvc见(2)式，图9为增量Δvc随δ的变化关系。

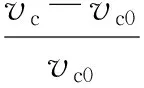
(2)

由图9可得：曲率半径r=40 mm条件下，Δvc随δ增大呈指数增加，δ=0.94r时的起爆速度较δ=0时增加35.6%，较平面带壳装药增加31.5%，偏移量继续增大将发生跳飞。因钨球实际水平穿壳厚度hθ随偏移量δ的增大而增大，穿透壳体消耗能量随之增多，起爆炸药也就变得困难。

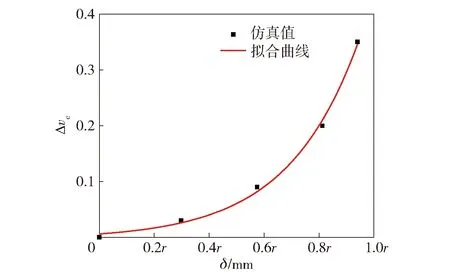
图9 临界起爆速度增量随偏移距离变化曲线Fig.9 Δvc vs. δ

为了消除碰撞点处壳体水平厚度hθ对炸药冲击起爆的影响，对hθ相同、偏移量δ不同时的炸药临界起爆速度进行计算，并与相同壳体厚度、不同偏移量δ时的垂直速度vv增量进行对比。图10为hθ=6 mm时临界起爆速度增量Δvc和h=6 mm时垂直速度增量Δvv随δ的变化关系。从图10可以看出：hθ=6 mm时Δvc随δ增大而缓慢增加，但差距低于5%，证明即使保证hθ相同，命中位置依然对柱壳装药冲击起爆产生影响；h=6 mm时垂直速度增量Δvv随δ变化非线性递减，差距至21%，说明滑移速度vs对炸药的冲击起爆起积极作用。

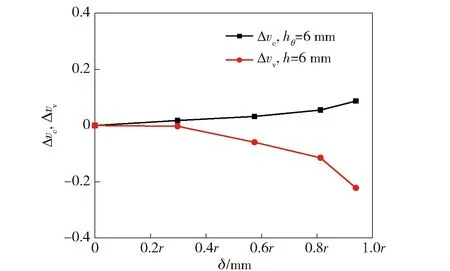
图10 临界起爆速度和垂直速度增量随偏移距离变化曲线Fig.10 Δvc and Δvv vs. δ

对钨球命中壳体不同位置时炸药起爆特性分析可得如下结果：

1)相同结构条件下，柱壳装药的起爆随碰撞点偏移量的增加而越困难；相同水平靶厚条件下，命中位置依然会影响柱壳装药冲击起爆。

2)偏移量δ≠0时起爆点并不在O1O2连线上，而是位于O1O2和v的夹角并距离壳体与炸药界面一定距离，起爆点位置不对称。

3)垂直速度vv、滑移速度vs均会对炸药起爆产生影响。

3.2 装药曲率半径对柱壳装药冲击起爆影响

取平面和柱壳装药(r=∞，r=40 mm)内观测点θ_1_2、观测点θ_1_3、观测点θ_1_4的压力进行比较。图11为v=3 000 m/s时观测点的压力时程曲线。冲击波到达平面带壳装药的时间早于柱壳装药，但相同位置处柱壳装药内的压力值高于平面装药。

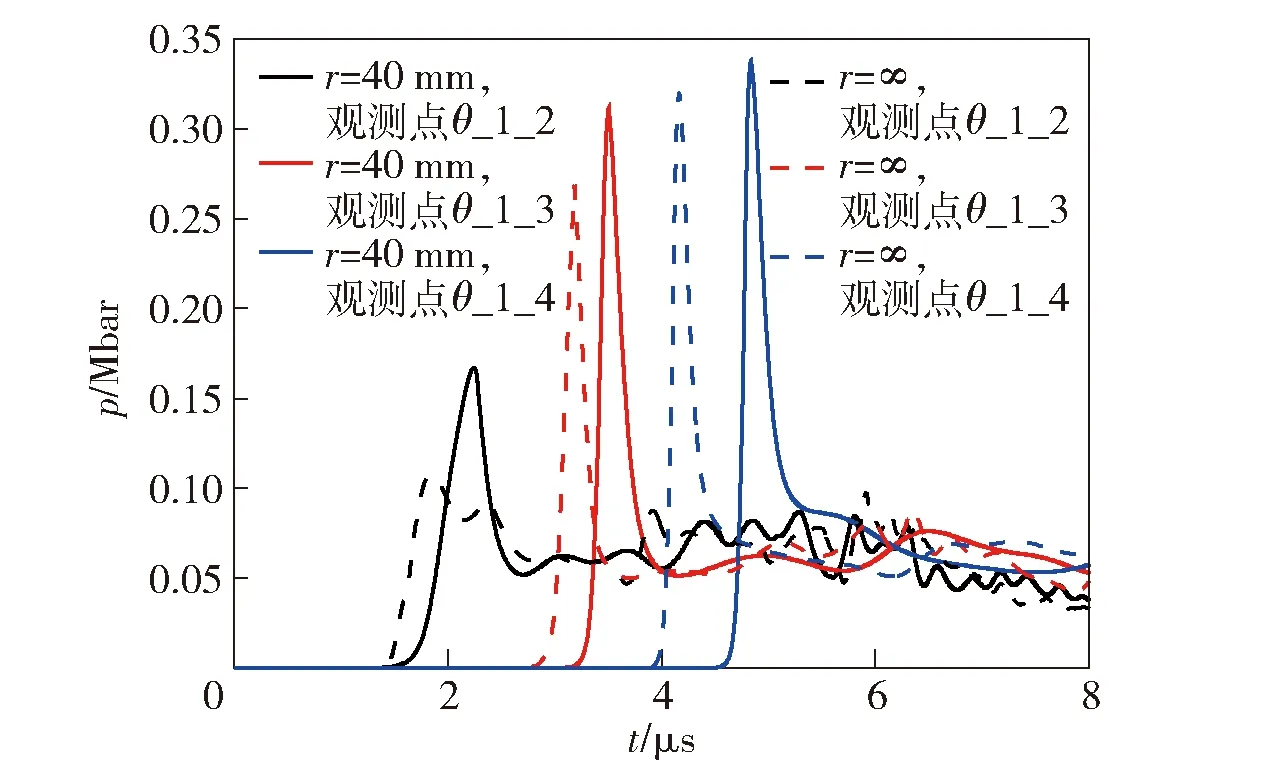
图11 柱形和平面带壳装药内观测点θ_1_2、观测点θ_1_3、观测点θ_1_4压力时程曲线(v=3 000 m/s)Fig.11 Pressure-time curves of Gauges θ_1_2，θ_1_3，θ_1_4 in cylindrical and plate charges (v=3 000 m/s)

利用应力波理论作定性解释，钨球撞击柱壳装药时，会在壳体和炸药界面处发生波系的反射和透射，在炸药中传入透射波。由于柱壳装药曲率半径小于平面带壳装药，传入的波系会因曲率的存在而发生汇聚，相同撞击条件下、炸药内同一位置处的压力值便高于平面带壳装药，因此，起爆柱壳装药易于起爆平面带壳装药。

为了得到装药曲率半径对柱壳装药临界起爆速度的影响关系，选取钨球撞击r分别为40 mm、60 mm、75 mm、100 mm、∞(平板)的Comp B炸药进行仿真计算。以r=∞时的起爆速度为基准做归一化处理，获得图12临界起爆速度增量随装药曲率半径倒数的关系。

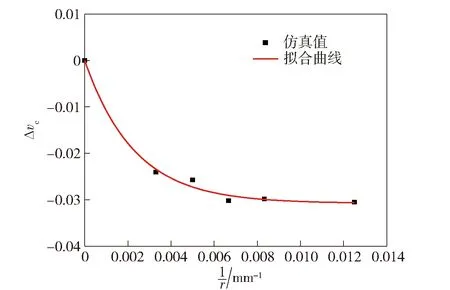
图12 临界起爆速度增量随曲率半径倒数的变化关系(δ=0)Fig.12 Δvc vs. 1/r (δ=0)

由图12可以看出：在偏移量δ=0时，临界起爆速度增量随1/r的增大非线性减小；r=∞(平板装药)时，装药临界起爆速度最大，较r=40 mm时提高3.2%.

4 结论

采用AUTODYN-3D仿真软件，对柱壳装药的冲击起爆特性开展研究，初步认清了柱壳装药的冲击起爆机理与规律，主要结论如下：

1)柱壳装药与平面带壳装药起爆过程相一致：起爆点位于炸药和壳体交界面一定距离。在临界起爆速度以上时，起爆位置随着速增加逐渐靠近交界面。相同条件下，起爆柱壳装药较易于起爆平面带壳装药。

2)命中位置对柱壳装药冲击起爆影响较大。临界起爆速度随偏移距离δ的增大呈指数增加，装药曲率半径r=40 mm条件下，δ=0.94r时的起爆速度较δ=0时增加35.6%，较平面带壳装药增加31.5%.

3)装药曲率半径对柱壳装药的冲击起爆有一定影响。临界起爆速度随曲率半径增加呈现非线性增大，偏移距离δ=0条件下，r=∞时起爆速度较r=40 mm时提高3.2%.

References)

[1] 江增荣,李向荣,李世才，等.预制破片对战斗部冲击起爆数值模拟[J].弹道学报,2009,21(1):9-13. JIANG Zeng-rong, LI Xiang-rong, LI Shi-cai, et al. Numerical simulation on shock initiation of performed fragment to warhead[J]. Journal of Ballistics,2009,21(1): 9-13.(in Chinese)

[2] 陈海利,蒋建伟,门建兵.破片对带铝壳炸药的冲击起爆数值模拟研究[J].高压物理学报,2006,20(1):109-112. CHEN Hai-li，JIANG Jian-wei，MEN Jian-bing. Numerical simulation of fragment impacting on charge with aluminum shell [J].Chinese Journal of High Pressure Physics,2006,20(1):109-112.(in Chinese)

[3] 李小笠,屈明,路中华, 等.三种破片对带壳炸药冲击起爆能力的数值分析[J].弹道学报,2009,21(4):72-75. LI Xiao-li, QU Ming, LU Zhong-hua, et al. Numerical analysis of impact initiation ability of three kinds of fragments on shell explosive [J]. Journal of Ballistics,2009, 21(4):72-75. (in Chinese)

[4] 童宗保,王金相,彭楚才，等.预制破片对屏蔽炸药冲击引爆研究[J].科学技术与工程,2013,14(7):173-177. TONG Zong-bao, WANG Jin-xiang, PENG Chu-cai, et al. Study onshock initiation of shielded explosive by prefabricated fragment [J]. Science Technology and Engineering, 2013,14(7):173-177. (in Chinese)

[5] 卢锦钊,智小琦,李娟娟，等.六棱柱破片冲击起爆带壳B炸药速度阈值研究[J].弹箭与制导学报,2016,36(1):82-84. LU Jin-zhao, ZHI Xiao-qi, LI Juan-juan, et al. Threshold velocity of hexagonal prism fragment impacting on Comp B with shell[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2016,36(1):82-84. (in Chinese)

[6] 陈卫东,张忠,刘家良，等.破片对屏蔽炸药冲击起爆的数值模拟与分析[J].兵工学报.2009,30(9):1187-1191. CHEN Wei-dong, ZHANG Zhong, LIU Jia-liang, et al. Numerical simulation and analysis of shock initiation of shielded explosive by fragment [J].Acta Armamentarii, 2009,30(9):1187-1191. (in Chinese)

[7] Held M. Initiation criteria of high explosive at different projectiles or jet densities [J] .Propellants, Explosives, Pyrotechnics, 1996, 21(5):235-237.

[8] Roslund L A . Initiation of warhead fragments I：normal impacts, NOLTR73-124 [R]. Dahlgren, VA， US：Naval Surface Weapons Center,1973.

[9] Lloyd R M. Conventional warhead systems physics and engineering design[M].Reston, VA,USA: Progress in Astronautics and Aeronautics,1998:502-504.

[10] 方青,卫玉章,张克明.射弹倾斜撞击带盖板炸药引发爆轰的条件[J].爆炸与冲击,1997,17(2):154-158. FANG Qing，WEI Yu-zhang，ZHANG Ke-ming，et al．On the projectile oblique-impact initiation conditions for explosive covered with a plate [J]. Explosion and Shock Waves, 1997, 17 (2):154-158. (in Chinese)

[11] 张先锋,赵有守,陈惠武.射弹冲击引爆带壳炸药临界条件[J].弹道学报,2006,18(4)57-59. ZHANG Xian-feng, ZHAO You-shou, CHEN Hui-wu. Thecritical condition of shelled explosive initiated by projectile [J]. Journal of Ballistics, 2006,18(4)57-59. (in Chinese)

[12] 明路遥,力昌坤,程波，等.爆炸冲击波作用下屏蔽装药模型起爆判据研究[J].四川兵工学报,2006,37(4):95-97. MING Lu-yao, LI Chang-kun, CHENG Bo, et al. Study oninitiation criterion of shielding charge model under explosion shock wave [J]. Journal of Sichuan Ordnance, 2006,37(4):95-97. (in Chinese)

[13] 傅华,谭多望,李涛，等.钨射弹引爆带壳板炸药阈值工程计算方法[J].含能材料,2008,16(1):100-102. FU Hua，TAN Duo-wang，LI Tao，et al．Engineering calculation on threshold velocity of covered explosives impacted by tungsten projectile [J].Chinese Journal of Energetic Materials, 2008, 16(1): 100- 102.(in Chinese)

[14] 宋浦,梁安定.破片对柱壳装药的撞击毁伤试验研究[J].弹箭与制导学报,2006,26(1)87-88. SONG Pu, LIANG An-ding. Experimental study on impact damage of fragment to cylinder charge [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006,26(1):87-88. (in Chinese)

[15] 辛建国,徐豫新,李超，等.破片冲击柱面薄壳装药实验[J].兵工学报,2014,35(2):222-227. XIN Jian-guo, XU Yu-xin, LI Chao, et al．Experiment of fragment impact on cylinder charge covered with thin shell [J]. Acta Armamentarii, 2014,35(2):222-227. (in Chinese)

[16] Lee E L, Tarver C M. Phenomenological model of shock initiation in heterogeneous explosive[J] Physics of Fluids, 1980, 23(12):2362.

[17] Murphy M J，Lee E L，Weston A M，et al. Modeling shock initiation in composition B[C]∥Proceedings of the 10th Detonation Symposium. Boston, MA, US: LLNL,1993.

[18] 贾宪振,陈松,杨建,等.双破片同时撞击对B炸药冲击起爆的数值模拟研究[J].高压物理学报, 2011,25(5):469-474. JIA Xian-zhen, CHEN Song, YANG Jian, et al. Numerical study of explosives initiation by simultaneous impact from two fragment [J]. Chinese Journal of High Pressure Physics,2011,25(5):469-474.(in Chinese)

Numerical Simulation on the Initiation of Cylindrical Covered Charge Impacted by Tungsten Sphere Fragment

WANG Xin, JIANG Jian-wei, WANG Shu-you, LI Mei

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

The interaction of tungsten fragment and cylindrical covered charge with different curvature radius is simulated by using AUTODYN-3D software. The influence of impacting position of fragment on the detonation characteristics of explosive is analyzed, and the “up-down” method is used to obtain the critical detonation velocity. The results show that the impact initiation progress of cylindrical covered charge coincides with that of plane covered charge. The detonation point is at a certain distance from the interface between explosive and casing, and gradually approaches to the interface as the fragment impact velocity increases. The cylindrical covered charge is easy to detonate under the same condition, and its critical detonation velocity increases nonlinearly with the increase in curvature radius. For collision point offsetδ=0, the critical detonation velocity is increased by 3.2% for infinite curvature radiusr=∞ compared with that forr=40 mm; the critical detonation velocity increases exponentially with the increase in offsetδ. Forr=40 mm, the critical detonation velocity forδ=0.94ris increased by 35.6% and 31.5% compared to that forδ=0 and plane covered charge, respectively.

ordnance science and technology; cylindrical covered charge; detonation point ;critical detonation velocity

2017-01-10

王昕(1990—)，女，博士研究生。E-mail:bitwangxin@bit.edu.cn

蒋建伟(1962—)，男，教授，博士生导师。E-mail:bitjjw@bit.edu.cn

TJ410.3+41

A

1000-1093(2017)08-1498-08

10.3969/j.issn.1000-1093.2017.08.006