求解逆矩阵的常用方法

张媛黑龙江工业学院

求解逆矩阵的常用方法

张媛
黑龙江工业学院

矩阵是线性代数中非常重要的内容之一，而在矩阵计算中最基础的就是求矩阵的逆矩阵。本文针对可逆方阵介绍几种常用方法，通过定义法、伴随矩阵法、初等变换法、分块矩阵法、以及Matlab软件的解法求逆矩阵,并从中总结出一些具有应用价值的规律。

初等变换；分块矩阵；伴随矩阵；可逆矩阵

矩阵是线性代数的主要内容，很多工作、生活中的实际问题用矩阵的思想去解决既简单又直观，而逆矩阵又是矩阵理论学习的重点与难点.本文给出几种求逆矩阵的常用方法，将会给矩阵的学习带来一定的帮助。

一、定义法

对于n阶方阵A,如果存在n阶方阵B使得AB=BA=E,则B=A-1，称A为可逆矩阵,称B为A的逆矩阵.下面举例说明这种方法。

例1设n阶方阵A满足方程A2-A-2E=0，证明A+2E可逆并求它的逆矩阵

二、伴随矩阵法

n阶矩阵A=aij为可逆的充分必要条件是A非奇异矩阵且

对于阶数低的小型矩阵用此方法求逆矩阵既方便又快捷，特别是对二阶矩阵只需要将主对角线元素互换，次对角线的元素变号.若所求矩阵是三阶以上的矩阵，计算量大容易出现误差，所以本方法适合二阶矩阵求逆矩阵。

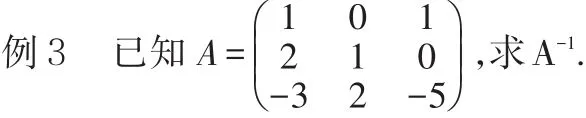
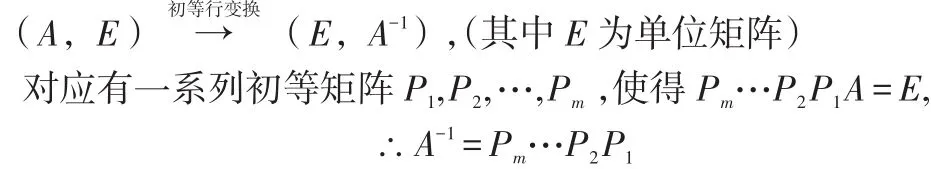
初等变换法适于阶数较高（n≥3）的矩阵，注意在求逆矩阵时只允许进行初等行变换，使用初等行变换法求逆矩阵一般比伴随矩阵法要简便一些。

三、初等变换法

设A，E都是n×n矩阵

这种方法不用事先知道n阶矩阵是否可逆，如果在化简过程中发现矩阵某一行全为零，则可知A不可逆。

四、分块矩阵法

设A、B、C、D分别为可逆矩阵，分两种情况进行讨论：

一种是对角形矩阵求逆，则有

此方法适用于阶数高的矩阵，并且能化成对角形或三角形块阵的矩阵。在求逆矩阵之前，要进行合理分块，不能一步完成的高阶矩阵，可通过分块降阶，反复使用上述方法。

五、Matlab软件解法

求逆矩阵还可以通过计算机软件Matlab，首先输入一个n阶矩阵A，然后利用函数det(A)判断行列式是否为零，如果不为零则可利用求逆矩阵函数inv(A)得到逆矩阵。

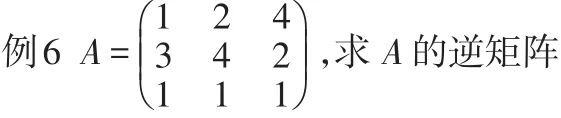
以上求逆矩阵的方法只是一些初步认识，通过归纳总结可以看出，在求逆矩阵的过程中，必须熟练掌握运用相关的可逆矩阵定理和性质，同时运用恰当的技巧可使计算更加简便.可逆矩阵的运用及其广泛，这就需要我们不断的去探索和研究。

[1]张海涛.逆矩阵的求法[J].大同职业技术学院学报，2004.

[2]王莲花,张香伟,李战国,王建平.求逆矩阵方法的进一步研究[J].河南教育学院学报（自然科学版）,2002.

[3]王建锋.求逆矩阵的快速方法[J].大学数学,2004.

[4]李桂荣.关于求逆矩阵方法的进一步探讨[J].德州高专学报, 2000.

张媛（1971-），女，汉族，单位：黑龙江工业学院，职称：副研究员，研究方向：高等数学。