利用狭义相对论计算洛伦兹力和安培力

陈彦儒 冯仕猛

(1上海交通大学机械与动力学院； 2上海交通大学物理与天文系，上海 200240)

利用狭义相对论计算洛伦兹力和安培力

陈彦儒1冯仕猛2

(1上海交通大学机械与动力学院；2上海交通大学物理与天文系，上海 200240)

随着对电磁现象研究的逐步深入，人们早已认识到磁现象来源于电荷的运动，磁场和电场是相互联系的统一体，称之为电磁场。本文根据狭义相对论中洛伦兹变换的基本原理，利用两个坐标系中静电力和电场的相对论变换，推导出洛伦兹力与库仑力、安培力之间关系，即洛伦兹力和安培力来源于电场力的相对论变换，从而更加有助于理解洛伦兹力的物理本质。

狭义相对论；电磁场；洛伦兹力;安培力

电场与磁场的产生都与电荷有关，它们的大小和方向又与电荷间的距离有关，还与电荷的运动速度有关。电场能够产生磁场，磁场也能产生电场，所以可以统称为电磁场。利用电磁场张量和四维力的协变性及电荷相对论的不变性，可以讨论电场力和安培力的相互转换[1-3]，但这种转换的前提是运动电荷中存在一个磁场，由此而可以推导出电磁场的相关变换关系。

经典物理教科书上较少介绍磁场的本质特征。本文利用相对论基本理论，讨论一个在惯性参考系内的两个并行运动电荷所受的电场力如何转换为另一个惯性参考系中的洛伦兹力，对进一步理解电磁场的相对论变换有一定的意义。

1 狭义相对论变换推导洛伦兹力和安培力

1.1 两个并行运动电荷产生的洛伦兹力

在经典电磁理论中，计算两个并行运动电荷之间的洛伦兹力时，总是首先计算一个运动电荷在空间某点产生的磁场强度，然后计算该点处运动电荷受到的洛伦兹力，如图1所示。

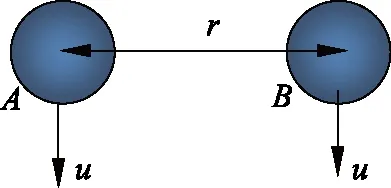
图1 两个并行运动的电荷图

在本文中，我们直接利用狭义相对论的基本理论来计算这个力。由狭义相对论，静止参照系S中A电荷在周围产生的电场强度为[4]

(1)

式中,u是电荷运动速度;q是电量;r是A电荷到空间某点之间的距离，z是空间某点与电荷运动方向之间的垂直距离。当A电荷沿如图1中的方向以u匀速运动时，A电荷在B处产生的电场强度表达式为

(2)

这样，静止坐标系S中B电荷受到的电场力为

(3)

在与电荷运动速度相同的参照系中S′中，A电荷产生的电场强度表达式为

(4)

在运动坐标系S′中，B电荷受到的电场力为

(5)

因为运动坐标系速度与运动电荷速度相同，根据狭义相对论中力的变换关系式[4，5]，把运动坐标中的力变换到静止坐标系中

(6)

式中F2是静止坐标系S中的力。把式(5)代到式(6)中可以得到

(7)

在S系看来，B电荷受到的力：一是利用电场的相对论变换式(3)得到的，另外一个力是通过相对论直接变换式(7)得到的，这两个力之差为

(8)

利用级数展开，式(8)可简单化为

(9)

式(9)表示在S系中两个运动电荷之间除了一个库仑力外，还存在一个其他力f，这与经典洛伦兹力表达式[4，5]完全相同，这说明通过力的相对论变换和场的相对论变换之差得到的S系中f就是洛伦兹力，也就是说，磁场完全可以通过相对论变换计算。

1.2 两个同方向运动电荷产生的洛伦兹力

对于两个电荷在一条直线上同方向的运动(或者反方向运动)，如图2所示。

图2 两个同方向运动电荷模型图

在S系中A电荷在B电荷处产生的电场强度和B电荷受到的力分别为

(10)

在与电荷速度相同的参照系S′中，电荷产生的电场强度为

(11)

式中r′是运动坐标系S′中两个电荷之间的距离，与图2中静止坐标系S系中两个电荷之间距离r的关系为

(12)

如此，在S′系中电荷之间的库仑力可以写成为

(13)

在狭义相对论中，如果电荷只有x方向有运动速度，而在y、z方向运动速度为零，则运动方向上力的相对论变换关系[4，5]

(14)

因此， 运动坐标中的力变换到静止坐标系S系中为

(15)

S系中的力，一个直接通过场的变换式(10)得到，另外一个是通过力的变换式(15)得到的，这两个力之差式(15)-式(10)可以得到

f=F2-F1=0

(16)

式(16)表示两个电荷在一条直线上作同方向运动时，它们之间只有库仑力，不受其他力作用，这与经典理论是吻合的。

因此，直接利用两个参照系中电场变换与力的变换，可以推导出洛伦兹力，这对正确理解洛伦兹力是非常有意义的。

1.3 直流长直导线安培力的相对论计算

对于两根直流长直导线(如图3所示)，设在长度为L0的导线内电子电量为Q。

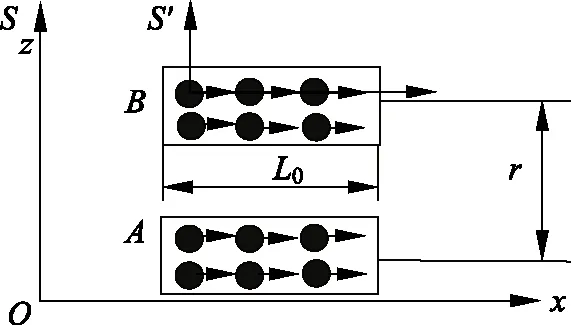
图3 两根直流导线的模型图

首先研究在静止的坐标系S系中电荷线密度的改变。在S系中，设A导线单位长度正电荷线密度是λ0+；当电子没有定向运动形成电流时，相同数量的正电荷占据的长度和相同数量的电子占据的长度相等。当电子定向运动速度为u，在S系中与正电荷相同的电子占据的空间导体长度在S系中收缩：

(17)

其中,L0是静止系中导线的原长；u是电子在导体内的运动速率。这样，S系中电子运动时线密度为

(19)

当正负电荷都静止时，有λ0-=λ0+=λ0，则在S系中净电荷线密度为

(20)

式中λ就是A导线中的净电荷线密度。利用无限长的带电长直导线在周围产生电场公式[4]

(21)

在S系中无限长的A导线中净电荷在周围产生的电场强度为

(22)

式中r是A导线到B导线之间的距离。在S系中B导线中运动的电子受到A导线中净电荷电场的库仑力为

(23)

用同样方法研究在与电子运动速度相同的运动坐标系S′系中A导线电荷密度的改变。在S′系中，电子单位长度线密度没有改变，即λ0-=λ0；但正电荷相对于电子的运动速度为-u。同样的道理，相同数量的正电荷占据的导体长度会在S′系中收缩：

(24)

这样，S′系中正电荷线密度为

(25)

则，在S′系中A导线净电荷线密度为

(26)

利用线电荷密度产生电场的公式[4]， 则在S′系中无限长的A导线中净电荷在周围产生的电场强度为

(27)

在S′系中B导线上运动电子受到的电场力为

(28)

利用式(6)两个坐标系中力的变换关系得到

(29)

在S系看来，B导线中运动电荷受到的力：一是利用电场的相对论变换式(23)得到的，另外一个力是通过相对论直接变换式(29)得到的。这两个力之差为

f=F1-F2=

(30)

将其进一步简化为

(31)

对于导线中运动电荷，一般情况下电荷速度远小于光速，式(31)可以进一步简化为

(32)

式(32)表示在S系中两根导线通过电流时，通过力和场的变换得到f与经典安培力表达式完全相同，说明了可以直接通过相对论变换计算安培力。

总之，利用两个参照系中电场和力的变换，可以推导出洛伦兹力与安培力，这对正确理解电磁场的相互转换是非常有帮助的。

2 结语

利用狭义相对论力和场的变换关系可以完整推导出安陪力和洛伦兹力与电荷间库仑力的关系，这对深入理解磁场的物理本质是非常有意义的。

[1] 黄永顺，李子军.相对论情形下相对静止运动电荷间的相互作用[J].漳州师范学院学报，自然科学版,2010(01):79-83.HuangYongshun,LiZijun.Theinteractionbetweenrelativelystationarymotionchargesintherelativisticcase[J].JournalofZhangzhouNormalUniversity,NaturalScienceEdition, 2010(01): 79-83. (inChinese)

[2] 张祥雪,程艳霞,范秀华,等.洛伦兹力可看作静止电荷所受电场力的相对论效应[J].物理与工程， 2006，16(4):26-30.ZhangXiangxue,ChengYanxia,FanXiuhua,etal.Lorenzforcecanberegardedastherelativisticeffectoftheelectricfieldforceofstaticcharge[J].PhysicsandEngineering, 2006, 4(16): 26-30. (inChinese)

[3] 戴孟昆.洛伦兹力的相对论解释[J].云南民族学院学报，自然科学,2001, 10(2):329-331.DaiMengkun.Lorenz’stheoryofrelativity[J].JournalofYunnanInstitutefornationalities,(NaturalScience), 2001, 4(2): 329-313. (inChinese)

[4] 高景，等.大学物理教程(上、下)[M].上海：上海交通大学出版社,2010.

[5] 赵凯华.电磁学[M].北京：高等教育出版社,2003.

[6] 费曼.费曼物理(中译本)第二卷[M].王子辅等，译.上海：上海科学技术出版社，2005:154.

■

USING SPECIAL RELATIVISTIC EFFECTS TO CALCULATE THE LORENTZ FORCE BETWEEN AND AMPERE’S FORCE

Chen Yanru1Feng Shimeng2

(1Faculty of Mechanical Engineering and Power Energy;2Department of Physics and Astronomy, Shanghai Jiaotong University, Shanghai 200240)

With the continuous development in research on electromagnetic phenomena, people already realize the fact that magnetic phenomena source from the movement of charges and magnetic and electric fields are interrelated unity, which is called electromagnetic fields. Based on the fundamental theory of Lorentz transformation in special theory of relativity, this paper attempts to examine the relationship among the Lorentz force, the Coulomb force and the Ampere’s force by employing the difference of charge density between two coordinate systems and the relativistic transformation of the electric field and electrostatic force. Lorentz force and Ampere’s force are derived from the relativistic transformation of the electric field force, which might facilitate the understanding of the physical nature of the Lorentz force.

special relativity; electromagnetic force; Lorentz force; Ampere’s force

2016-08-05；

2017-02-28

陈彦儒，男,上海交通大学机械与动力工程学院学生；冯仕猛，男，副教授，主要研究方向为基础物理，smfeng@sjtu.edu.cn。

陈彦儒，冯仕猛. 利用狭义相对论计算洛伦兹力和安培力[J]. 物理与工程，2017，27(4)：75-78.