一种同时测量高斯光束束腰位置和半径的新方法
2017-09-01黄水平
黄水平
(宁波大学理学院,浙江 宁波 315211)
一种同时测量高斯光束束腰位置和半径的新方法
黄水平
(宁波大学理学院,浙江 宁波 315211)
从高斯光束的横向光强分布特性出发,建立了小孔光阑透过光功率与高斯光束束腰位置、束腰半径、光阑孔径和光阑位置间的关系式。用氦氖激光器、凸透镜、小孔光阑和硅光电池等搭建了一套简单测量装置,利用此装置对同一小孔光阑在高斯光束传播方向上不同位置时的透过光功率进行了测量。用所得的理论公式对实验数据进行拟合,通过拟合出的参数可同时测得高斯光束的束腰位置和半径。测量结果表明,该方法不仅合理、可行,而且具有装置简单、操作方便等优点。
高斯光束;束腰半径;束腰位置;同时测量
高斯光束的束腰半径和束腰位置是激光束的重要参数。在激光传播方向上的某位置处,测量高斯光束光斑半径有多种方法,如针孔扫描法、狭缝扫描法[1]、刀口扫描法[2,3]、CCD法[4]、扫描Ronchi刻尺法[5]和激光散斑法[6]等。这些方法各具优点,但均有不足。实际测量中,由于高斯光束束腰位置不易准确判断,用上述方法测量高斯光束的束腰半径相对困难。现有文献中,为测量高斯光束的束腰半径,通常是先测出激光传播方向上多个不同位置的光斑半径,再利用光斑半径与位置的关系式拟合出束腰半径,或通过方程组求解出束腰半径[7-10]。由于需要对多处的光斑半径进行测量,测量过程相对复杂和繁琐。本文根据高斯光束的横向光强分布和光斑半径公式,在推导出小孔光阑透过光功率表达式的基础上,提出了一种可同时测量高斯光束束腰位置和半径的新方法。
1 测量原理
根据高斯光束的性质,与束腰距离为z处的横截面内,高斯光束的场振幅分布可表示为[11,12]
(1)
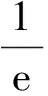
(2)
式中,ω0为束腰半径;λ为激光波长。
若在激光束z处横截面上加一孔半径为R的小孔光阑(小孔中心与光束中心重合),则从小孔中透过的光功率为
(3)
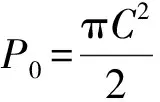
将式(3)变换可得
(4)
在实际测量中,小孔光阑的位置读数z并非从束腰算起。设束腰位置坐标为z0,则式(4)中的z应变为z-z0,由此可得

(5)
上式可看成是如下形式的函数
y=Az2+Bz+C
(6)
其中,
(7)
由此可知,若测出小孔光阑在激光传播方向上不同位置z处的透过功率P(z),再通过二次多项式拟合得到系数A,B和C,可测出高斯光束的束腰位置z0,束腰半径ω0及小孔半径R,即
(8)
2 实验装置
图1为实验装置示意图。具体说明如下。

图1 测量装置示意图
高斯光束经衰减片衰减和凸透镜变换后照射在小孔光阑和光电池上,小孔光阑和光电池紧贴在一起并安放在三维调节架上,以便于对其位置进行较精密的调节并得到较准确的读数。使用衰减片是为了保护光电池并减小光电池串联的外接电阻值。从光电池的光照特性可知,在光电池的特性参数中,与入射到光电池上的光强或光功率成线性关系的是光电池的短路电流[13],而只有在外接负载电阻(包括仪表内阻)RL≪Rd(Rd为光电池内阻)时,才可认为接近短路。Rd一般属低值范围,而且其大小会随光强的增加而急剧下降。使用凸透镜是为了让高斯光束在变换后的束腰处于合适的位置(透镜变换前,高斯光束的束腰在氦氖激光器外壳内部平面输出镜处),以便在束腰处用针孔扫描法再次对束腰半径进行验证性测量。测量中要求小孔和激光束处于对心状态,这可从光电流的读数是否最大来判断。
实验中,让小孔光阑和光电池从激光器前的某个位置开始沿着光轴方向移动,依次测出小孔光阑在不同位置时的光电流大小(透过小孔光功率的相对值),利用式(6)拟合出A、B和C的数值后,可进一步利用式(8)得到高斯光束的束腰位置和束腰半径。
3 实验结果
表1为用图1装置测出的小孔光阑在不同位置时的透过光功率和对应的y值。利用式(6)对表1数据进行拟合所得的拟合曲线如图2所示。从图2可以看出,除个别数据点外,拟合曲线与测量数据能较好地吻合。

表1 小孔光阑在光轴上不同位置时对应的光功率
上述拟合得到的拟合参数A、B、C以及由式(8)计算出的激光束腰半径ω0、束腰位置z0、小孔光阑半径R见表2。

表2 由二次多项式拟合表1数据所得结果
实验中采用的小孔光阑孔直径的标定值为1.00mm,可以发现,拟合出的孔径值与标定值很接近。
为进一步验证上述拟合结果,根据拟合出的激光束腰位置,用针孔扫描法对束腰处的横向光强分布进行了测量,并用以下公式对横向光强分布的测量结果进行拟合,可再次到得束腰半径[14]:
(9)
式中,I(r)为束腰横截面上位置r处的光强。
表3为用针孔扫描法测出的束腰横截面上不同位置处的相对光强大小。用公式(9)对表3数据进行拟合所得的拟合曲线如图3,拟合出的高斯光束束腰半径为ω0=0.464mm,与前面的拟合结果(0.447mm)基本一致。
4 结论
在分析传统测量方法不足的基础上,根据高斯光束横向光强分布特性,推导了小孔光阑在激光传播方向上任一位置透过光功率的表达式,用自行搭建的实验装置对小孔光阑在不同位置的透过光功率进行了测量。用推导出的公式拟合测量数据,可同时获得高斯光束的束腰位置、束腰半径等参数。在拟合出的束腰位置处,用针孔扫描法对束腰半径进行了验证性测量。结果表明,通过拟合小孔光阑在不同位置时的透过光功率来同时测量激光束腰位置和半径,不仅合理可行,在实验操作上也更为简单和方便。
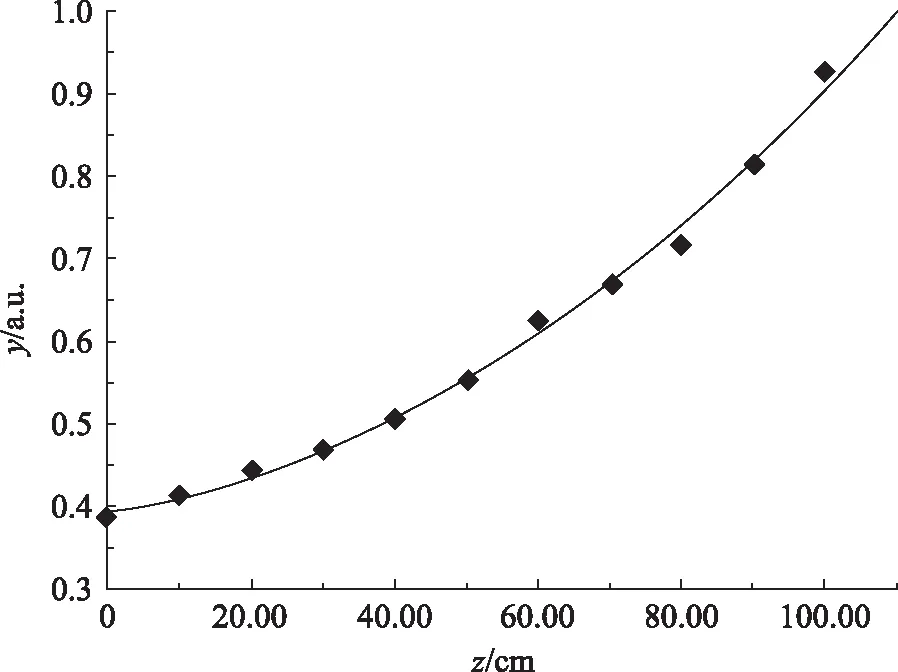
图2 小孔光阑在不同位置时光功率的二次多项式拟合曲线
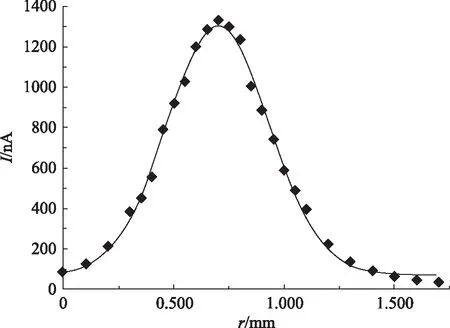
图3 激光束腰处不同位置点的光强拟合曲线

r/mm00.1000.2000.3000.3500.4000.4500.5000.550I/nA881302173854555607919261031r/mm0.6000.6500.7000.7500.8000.8500.9000.9501.000I/nA120212891333130112371009889745593r/mm1.0501.1001.2001.3001.4001.5001.6001.700I/nA49239922613794665039
[1] 蔡伯荣.激光器件[M].湖南:湖南科学技术出版社,1981:38-39.
[2] 熊小华.刀口法测量高斯光束腰斑大小实验设计[J].南京航空工业学院学报,2000,14(3):1-3. Xiong Xiaohua. Design of experiment for measuring Gaussian beam spot size using knife edge[J]. Journal of Nanchang Institute Of Aeronautical Technology, 2000, 14(3): 1-3. (in Chinese)
[3] Bilger T H, Habib R. Knife-edge scanning of an astigmatic Gaussian beam [J]. Applied optics, 1985, 24(5): 686-690.
[4] 梁明,谷开慧,孙晓冰.基于CCD对高斯光束进行实时判断[J].大学物理实验,2015,28(1):9-12. Liang Ming, Gu Kaihui, Sun Xiaobing. Based on CCD for Gaussian beam real-time judgment and measuring characteristic parameters[J]. Physical Experiment of College, 2015, 28(1): 9-12. (in Chinese)
[5] Cherri A K, Awwal A A S, Karim M A. Generalization of Ronchi, Sinusoidal, and Triangular Nulings for Gaussian-laser-beam-diameter measurements [J]. Applied Optics, 1993, 32(13): 2235-2242.
[6] 姚昆,侯碧辉,张增明,等.散斑位移法测高斯光束的空间分布[J].强激光与粒子束,2000,12(2):141-144. Yao Kun, Hou Bihui, Zhang Zengming, et al. Measurement of space distribution of laser Gaussian beam by speckles displacement method[J]. High Power Laser and Particle Beams, 2000, 12(2): 141-144. (in Chinese)
[7] 樊心民,郑义,王冠军,等.90/10刀口法测量高斯光束束腰的两种计算方法[J].应用激光,2008,28(2):139-141. Fan Xinmin, Zheng Yi, Wang Guanjun, et al. Two calculation methods for measuring the beam waist of Gaussian laser beam using a 90/10 knife-edge method[J]. Applied Laser, 2008, 28(2): 139-141. (in Chinese)
[8] 杨晓东,谭锦业,刘定文,等.高斯光束特性试验研究[J].实
验室研究与探索,2010,29(8):23-25. Yang Xiaodong, Tan Jinye, Liu Dingwen, et al. Experimental investigation of the Gauss beam’s property [J]. Research and Exploration in Laboratory, 2010, 29(8): 23-25. (in Chinese)
[9] 李文成,谷晋骐,王涌萍.激光光斑及束腰光斑尺寸的测量研究[J].应用光学,2002,23(3):30-33. Li Wencheng, Gu Jinqi, Wang Yongoing. Research on laser spot and beam waist spot size measurement[J]. Journal of Applied Optics, 2002, 23(3): 30-33. (in Chinese)
[10] 王垚廷,张瑞红,李光耀,等.高斯光束束腰位置及尺寸的精确测量[J].西安工业大学学报,2015,35(6):431-433. Wang Yaoting, Zhang Ruihong, Li Gguangyao, et al. Precise measuring Guassian beam parameter[J]. Journal of Xi’an Technological University, 2015, 35(6): 431-433. (in Chinese)
[11] 邱元武. 激光技术和应用[M]. 上海: 同济大学出版社, 1997: 42-57.
[12] 王涛,吴福全,马丽丽,等.尼科耳棱镜对单模高斯光束光强分布的影响[J].物理实验,2008,28(4):1-5. Wang Tao, Wu Fuquan, Ma Lili, et al. Effects of Nicol prism on the intensity distribution of single-mode Gaussian light beam[J]. Physics Experimentation, 2008, 28(4): 1-5. (in Chinese)
[13] 唐爽,岑剡.利用硅光电池测量硅单晶半导体材料的禁带宽度[J].物理实验,2008,28(11):6-8. Tang Shuang, Cen Yan. Measuring the band gap of silicon using silicon photocells[J]. Physics Experimentation, 2008, 28(11): 6-8. (in Chinese)
[14] 黄水平,郭旭东,张飞雁,等.拟合法测量高斯光束的束腰半径[J].物理实验,2010,30(3):29-31. Huang Shuiping, Guo Xudong, Zhang Feiyan, et al. Measurement of waist radius of Gaussian beam by fitting method[J]. Physics Experimentation, 2010, 30(3): 29-31. (in Chinese)
■
A NEW METHOD FOR SIMULTANEOUSLY MEASURING WAIST POSITION AND WAIST RADIUS OF GAUSSIAN BEAM
Huang Shuiping
(College of Science, Ningbo University, Ningbo Zhejiang 315211)
Based on the transverse light intensity distribution of Gaussian beam, the relationship among the light power, the waist position and the waist radius of Gaussian beam, the aperture of diaphragm and the position of diaphragm was derived. A simple measuring installation was built using a He-Ne laser, a convex lens, a diaphragm and a Silicon Photocell. The light power transmitted out of the diaphragm, which was placed in the different positions along the propagation direction of Gaussian beam respectively, was measured using the measuring installation. The waist position and the waist radius of Gaussian beam were measured simultaneously by fitting the measured data with the derived formula. The results show that the proposed method is not only appropriate and feasible, but also simple and convenient.
Gaussian beam; waist position; waist radius; simultaneous measurement
2016-12-24;
2017-03-05
浙江省高校实验室工作研究项目(Y201310)。
黄水平,男,副教授,主要从事薄膜光学、光电检测方面研究和近代物理实验教学工作,huangshuiping@nbu.edu.cn。
黄水平. 一种同时测量高斯光束束腰位置和半径的新方法[J]. 物理与工程,2017,27(4):30-33.
