A geometric feature ofthe Newton law ofgravitation

Zhang Meirong(1.Departmentof Mathematical Sciences,Tsinghua University,Beijing 100084,China; 2.Zhou Pei-Yuan Center for Applied Mathematics,Tsinghua University,Beijing 100084,China)

A geometric feature ofthe Newton law ofgravitation

Zhang Meirong1,2
(1.Departmentof Mathematical Sciences,Tsinghua University,Beijing 100084,China; 2.Zhou Pei-Yuan Center for Applied Mathematics,Tsinghua University,Beijing 100084,China)

In the Newton law of gravitation,the mostmiraculous factis thatthe gravity is reciprocally proportionalto the square ofthe distance between particles.In this paper,by assuming thatthe gravity is along with the line passing through particles and is proportionalto the productofmasses ofparticles, we willshow thatthe above factis equivalentto the geometric requirementthatthe gravity between two homogeneous balls is equal to that between two particles of the same masses located at the centers of balls.In fact,this will lead to a second-order Euler equation whose physicalsolution is reciprocally proportionalto the square ofthe distance.

Newton law ofgravitation;geometric feature;integralequation;Eulerequation

1 The statement

Based on the three laws of Kepler on motions of planets in the solar system,Newton has proposed three laws on motions ofparticle systems.By considering sphericalplanets as particles located atthe centers ofballs,Newton has applied his invention of Calculus of Differentiation and Integration to give a rigorous mathematical deduction and then to obtain the gravitation law.This is the greatestachievementand the starting pointof modern sciences.All of these have been given inmasterpiece MathematicalPrinciples of Natural Philosophy[1].

The gravitation law is now elementary to schoolboysand girls and can be stated as follows.Given two particles ofmasses milocated at pi∈R3,i=1,2,where p1/=p2,the gravity ofthe particle m1by the particle m2is such a vector∈R3that

(F1)→F is along with the direction from p1to p2,

(F2)‖→F‖is proportionalto the productof the masses,and

(F3)‖→F‖is reciprocally proportionalto the square ofthe distance between the particles.

Mathematically,by denoting

where G＞0 is the gravity constant.

With the gravitation law(2)forparticles athand,itis a standard factthatthe gravity between two homogenous balls can be reduced to thatfortwo particles of the masses same as the balls located atthe centers ofballs.Moreover, by solving the motion equations ofparticles,one can recoverthe Kepler′s three laws for motions of planets,as did in the usualtextbooks on Ordinary DifferentialEquations,See[2].

The mostmiraculous conclusion in the gravitation law(2)is Fact(F3),i.e.,‖‖is reciprocally proportionalto r2,the square of the distance between the particles.In this paper,based on Facts(F1)and(F2),we will show that Fact(F3)is equivalentto the following geometric requirement.

(F4)The gravity between two homogeneous balls is equalto thatbetween two particles of the same masses located atthe centers ofthe balls.

Letus describe this in a mathematicalway.Given two particles of masses milocated at pi∈R3,i=1,2, p1/=p2,from Facts(F1)and(F2),the gravitybetween them is given by

(A)The function f(r)is continuous and strictly decreasing.

By using formula(3),for two homogenous matters of totalmasses milocated in the spatialdomainsΩi⊂R3, i=1,2,Ω1∩Ω2=∅,the gravity between them is given by the following multi-dimensionalintegral

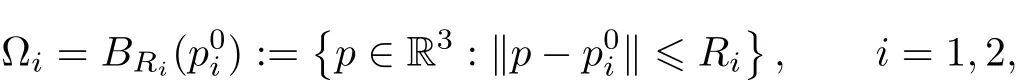
are balls,where

Thus the geometric requirement(F4)is the following equation forthe function f

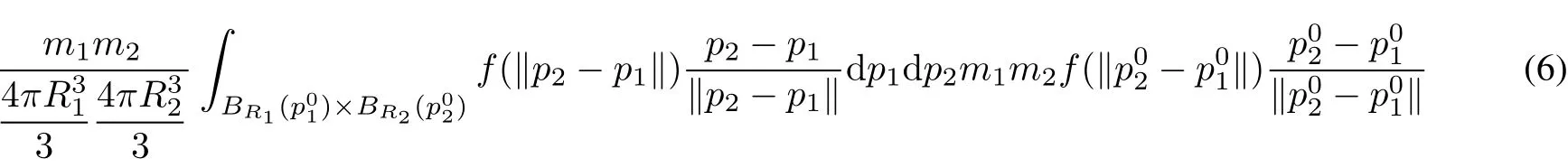
forallparametersas in(5).The main resultis as follows.

Theorem Under assumption(A)on f,the unique solution of Eq.(6)is given by

where k is a positive constant.

2 The proof

Eq.(6)is a linear integral equation for f,where the masses miare irrelevant.Henceforth we assume that m1=m2=1.

Now we give a rigorousreduction to Eq.(6).Firstofall,the geometric requirement(F4)can be reduced to the case thatone ofthe balls shrinks into a particle,say thatis a point.Going back to Eq.(6),this can be stated as follows.

Lemma The function f satisfies Eq.(6)for allparameters as in(5)if and only if f satisfies

for allparameters satisfying

Proof The sufficiency.Letus assume(8)for allballs and allparticles.To obtain(6),by considering d p2as a particle located at p2∈BR2()of the mass

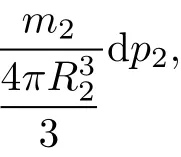
itfollows from assumption(8)that

With this athand,by applying(8)again,one has

Thus Eq.(6)is obtained.

The necessity.Letus take m1=m2=1 in(6).By taking the limitof(6)as R2→0,one can obtain Eq.(8).

Now we give the proof of the theorem.Due to the lemma above,we need only to solve Eq.(8).As for parameters in(9),withoutloss of generality,letus take=O,the origin,and=(0,0,L)in the upper z-axis. By rewriting R1as R,we know that L and R satisfy

Then the left-hand side of(8)is

Due to the symmetry of BR(O),one has

The right-hand side of(8)is simply(0,0,f(L)).Hence Eq.(8)is reduced to

The quantity Fzof(11)can be reduced to

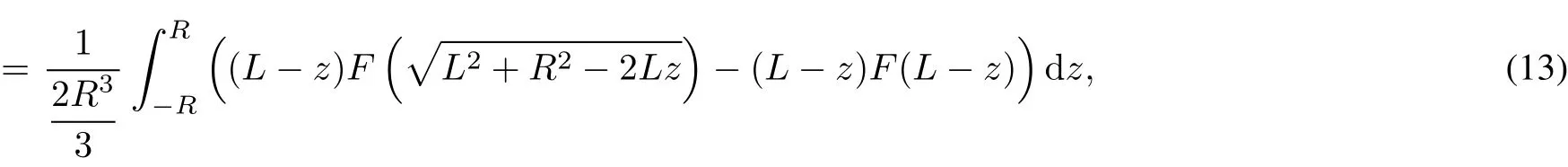
where F:(0,∞)→R is an anti-derivative of f

and by using the change s=L−z for variables,one has

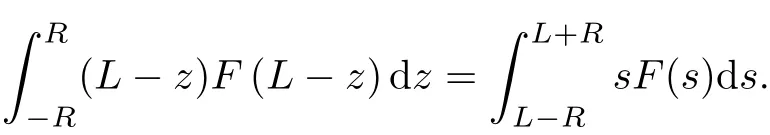
Substituting into(13),we obtain

As a consequence,Eq.(12)is

where L and R,as in(10),are arbitrary.

Some observation on Eq.(15)is as follows.In case f(s)≡1/s2,by taking F(s)=−1/s,the left-hand side of(15)is Hence f(s)=1/s2satisfies Eq.(15).In case f(s)≡s,by taking F(s)=s2/2,the left-hand side of(15)is

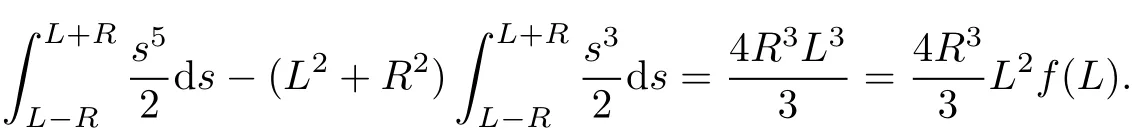
We know that f(s)=s also satisfies Eq.(15).

Due to assumption(A),f is continuous.By(14),F is of class C1.Thus the left-hand side of(15)is of class C2in L.Hence Eq.(15)shows that f is of class C2.Inductively,we conclude from Eq.(15)that f is of class C∞.

Differentiating(15)with respectto R,itfollows from the Newton-Leibnitz formula that

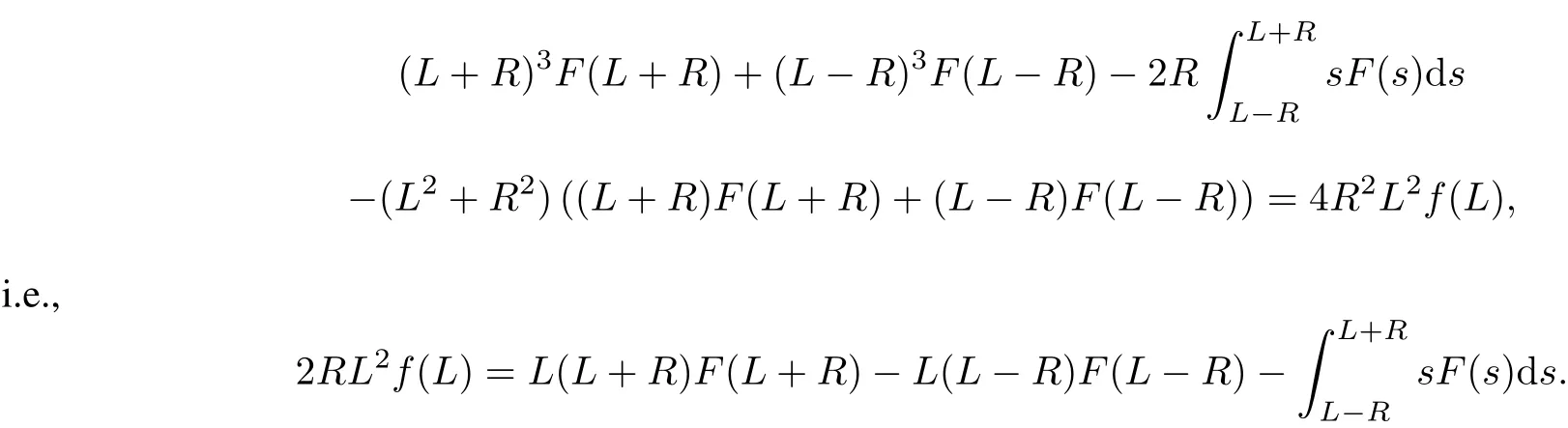
Differentiating itwith respectto R again and using(14),we have

Furtherdifferentiation with respectto R gives

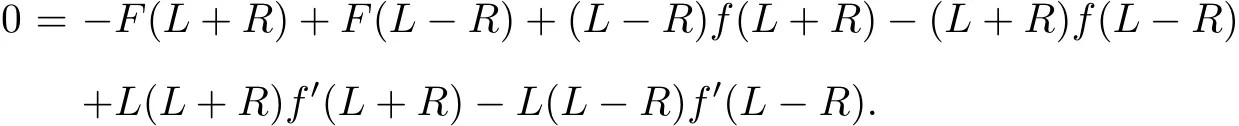
Differentiating itwith respectto R again,we have

By letting R↓0 in this equation,we obtain

By denoting r:=L,this is a second-order Euler equation

Eq.(16)can be solved by the standard change s=log r∈R for variables,which leads to

Solving this equation,we obtain

Hence solutions of Eq.(16)are

Finally,as we are considering decreasing solutions f(s),cf.assumption(A),it is easy to exclude the case/=0 in(17).Hence we have the desired result(7)and complete the proofofthe theorem.

Remark Eq.(16)can also be obtained by using the Taylorexpansion.Letus rewrite Eq.(15)as

As a function of R∈(0,L),the left-hand side of(18)is cubic in R.Let us expand the right-hand side of(18)at R=0.When s→0,one has

Similarly,one has

By recalling(14),we obtain

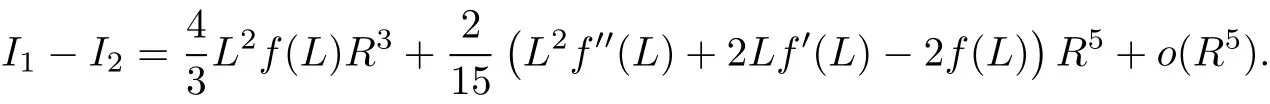
Comparing with Eq.(18),we also arrive atthe Euler equation(16)for f.

In conclusion,under(F1)and(F2),the gravity is reciprocally proportionalto the square ofthe distance is the same as the geometric requirementthat the gravity between two balls is equalto that between two particles of the same masses located at the centers of balls.Such a geometric requirement was presumably assumed by Newton because the planets have been considered as particles.

O 175,O31 Document code:A Article ID:1000-5137(2017)03-0432-07 2010 MSC:70F99,34A05

10.3969/J.ISSN.100-5137.2017.03.012

date:2017-03-21

This research was supported by the National Natural Science Foundation of China(No.11231001, 11371213).

Zhang Meirong,professor,reseach area:Dynamical systems,E-mail:mzhang@math.tsinghua. edu.cn

[1]Newton I.Mathematicalprinciples of naturalphilosophy[M].Chicago:Encyclopaedia Britannica Inc,1952.

[2]Betounes D.Differentialequations:theory and applications,2nd editon[M].New York:Springer-Verlag,2010.