Lie symmetry analysis and conservation laws for the time fractionalfourth-order evolution equation

Wang Li,Tian Shoufu,Feng Lianli,Song Xiaoqiu(Schoolof Mathematics,China University of Mining and Technology,Xuzhou 221116,China)

Lie symmetry analysis and conservation laws for the time fractionalfourth-order evolution equation

Wang Li,Tian Shoufu∗,Feng Lianli,Song Xiaoqiu∗
(Schoolof Mathematics,China University of Mining and Technology,Xuzhou 221116,China)

In this paper,we study Lie symmetry analysis and conservation laws for the time fractional nonlinear fourth-order evolution equation.Using the method of Lie point symmetry,we provide the associated vectorfields,and derive the similarity reductions of the equation,respectively.The method can be applied wisely and efficiently to getthe reduced fractionalordinary differentialequations based on the similarity reductions.Finally,by using the nonlinear self-adjointness method and Riemann-Liouville time-fractionalderivative operator as well as Euler-Lagrange operator,the conservation laws ofthe equation are obtained.

Lie symmetry method;symmetry analysis;conservation laws

2000 MSC:35Q51,35Q53,35C99,68W30,74J35

1 Introduction

As we allknow,the Lie group oftransformations theory,was initially constructed by the Norwegian mathematician Sophus Lie in the early 19th century,which has been widely studied in differentialequations[1−12],particularly in partialdifferentialequations(PDEs)with multi-componentsystems.In recentyears,itis importantto investigate the fractionaldifferentialequations(FDEs)because ofmore and more applications in various fields[13−16]:systems identification,fluid flow,control problems,signal processing,viscoelastic materials,polymers,fluid mechanics, physics,economics,biology,engineering and so on.Actually,the symmetry analysis of FDEs and the fractional derivatives are proposed by Gazizov and his collaborators in[17].Readers can refer to[18–22]for further details. In[23],the famous Noethertheorem connects the symmetry theory with conservation laws of differentialequations, which exist Euler-Lagrange equations.In addition,in order to look for conservation laws of FDEs,Frederico et al.[24−28]have provided fractionalgeneralizationsof Noethertheorem.However,it’s limited formany FDEs to deal with fractionalgeneralizations.Then,a generaltheorem on conservation laws forarbitrary differentialequations[29]wasproposed by Ibragimov.Based on it,Lukashchuk[30]proposed NoetheroperatorswithoutfractionalLagrangians and proved fractional generalizations of the Noether operator.In[31],in order to get the conservation laws,the authors applied the fractionalgeneralizations of the Noether operators to the time-fractionalKompaneets equations.

In this paper,we study the Lie symmetry analysis to the time fractionalnonlinearfourth-orderevolution equation

where u=u(x,t),h1,h2,h3and h4are constants.Whenα=1,h1=−2,h2=−1,h3=−2,h4=1,the time fractionalequation becomes the following nonlinear fourth-orderevolution equation

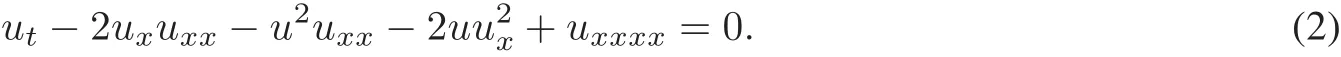
Some new exactsolutions of Eq.(2)are given in[32].

The paper is divided into five parts.In Section 2,some properties analyzing FDEs of Lie group method,and the associated infinitesimalgenerator are introduced.In Section 3,we obtain the corresponding similarity reduction of Eq.(1).Section 4 is devoted to constructthe conservation laws.Finally,some conclusions and discussions are present.

2 Lie symmetry analysis

In this section,we investigate the time fractional nonlinear fourth-order evolution equation by means of Lie symmetry.First we recall,some basic properties of Lie symmetry analysis of FDEs.Here is the definition of Riemann-Liouville fractionalpartialderivative in[21].

Definition 1[21]The Riemann-Liouville fractionalpartialderivative is defined by

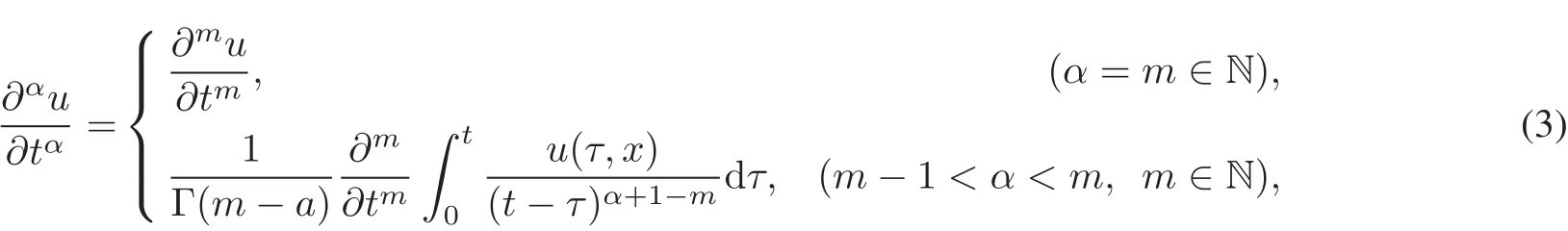
Consider a time fractionalFDE with two independentvariables

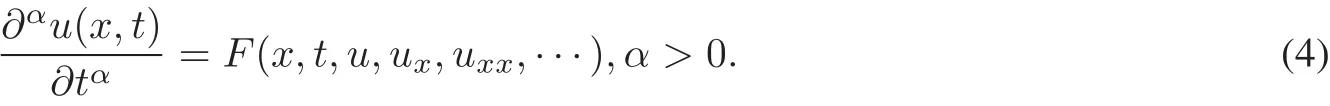
One-parameterpointtransformationsof Lie group is given by

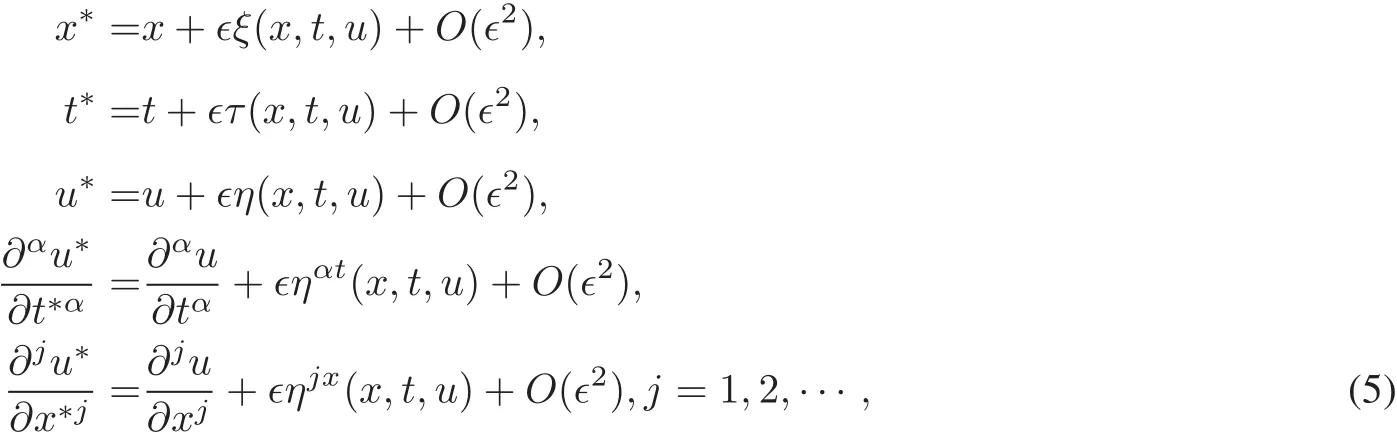
where∈is the group parameter,andξ,τ,ηare infinitesimals.In addition,we considerthe following infinitesimal generator

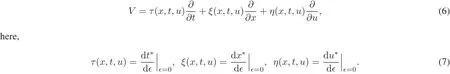
Based on the infinitesimalinvariance criterion,we find the infinitesimalgeneratormustsatisfy

In addition,when the infinitesimalηis linear to u,µis invalid[19].

Now,we apply the above Lie symmetry analysis method above all to the Eq.(1),and obtain the following theorem.

Theorem 1 The vectorfields ofthe time fractionalfourth-orderevolution equation is given by

Proof Substituting(9)and(10)into(1),we find the following symmetry equation

by the condition that variables ux,ut,uxt,uxx,utt,uxxt,···an,for n=1,2,···of u are independent.Taking(10)-(13)into consideration,and making each power of the derivatives of u is equalto 0,we getthe determining equations

Solving(16),we find

where,a1,a2are arbitrary constants.So the associated vectorfields are given by

3 The similarity reduction

In this section,the similarity reduction for the time fractional nonlinear fourth-order evolution equation is obtained.Similar to the definition of group invariantsolution of PDEs[4,33],the group invariantsolution of FDEs is defined.

Definition 2[4,33]If u=v(x,t)satisfies Eq.(1),and u=v(x,t)is an invariant surface of(6),i.e.,it correspondsto the invariantsurface conditionτ(x,t,v)vt+ξ(x,t,v)vx=η(x,t,v),then u=v(x,t)is an invariant solution of Eq.(1)relating to the infinitesimalgeneratorof(6).

Forthe symmetry of V1of(18),we give the characteristic equation

and the corresponding invariants are

Theorem 2 The time fractionalnonlinear fourth-orderevolution equation is reduced to the nonlinear ordinary differential equation(ODE)of time fractional order in the following by means of similarity transformation u=and the similarity variable z=,

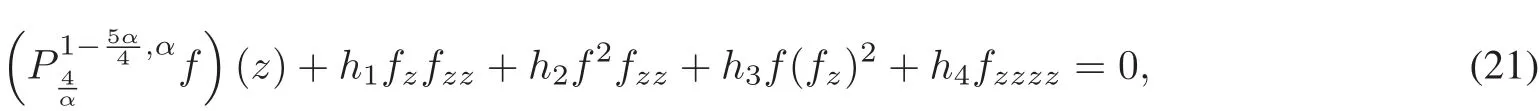
with the Erd´elyi-Koberfractionaldifferentialoperatorof order[34]

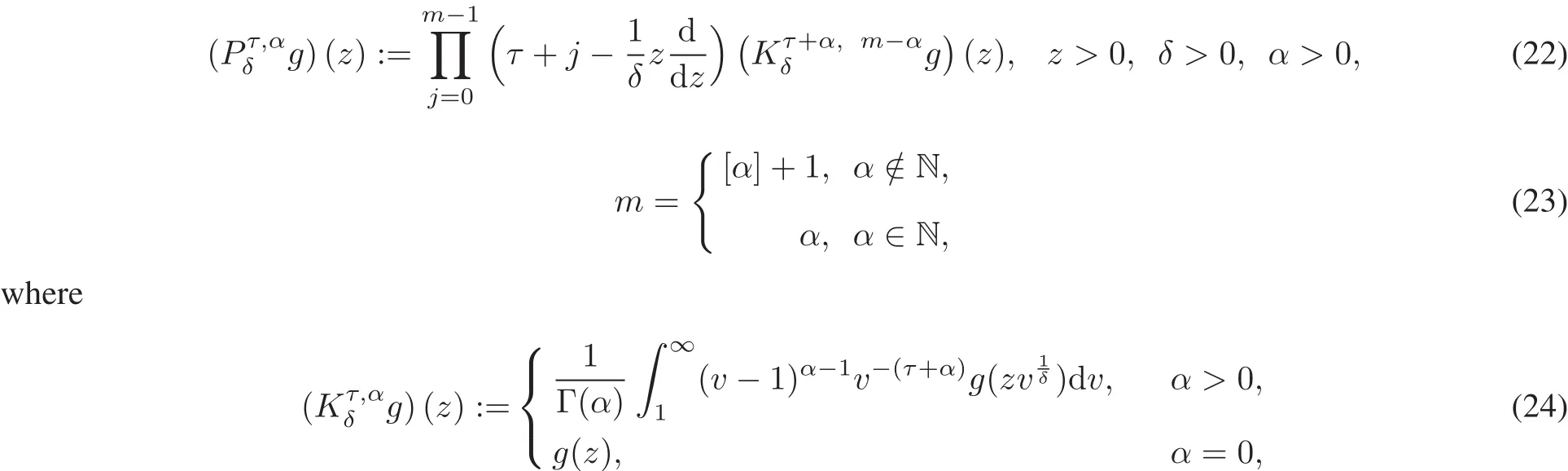
is the Erd´elyi-Koberfractionalintegraloperator.

Proof Let n−1＜α＜n,n=1,2,···,then we obtain the similarity transformation of Riemann-Liouville fractionalderivatives as follows

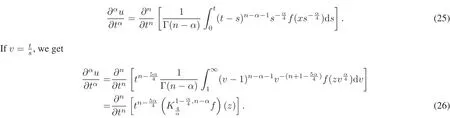
Considering the relation of z=,we get

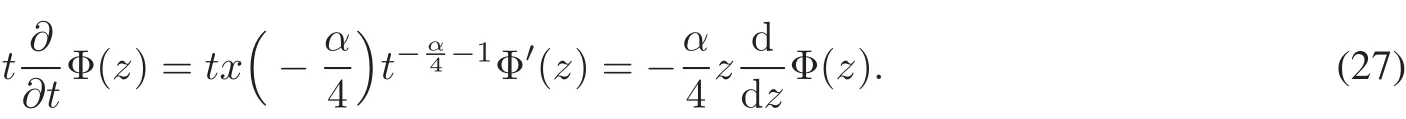
Hence,the simplification of the above equation is

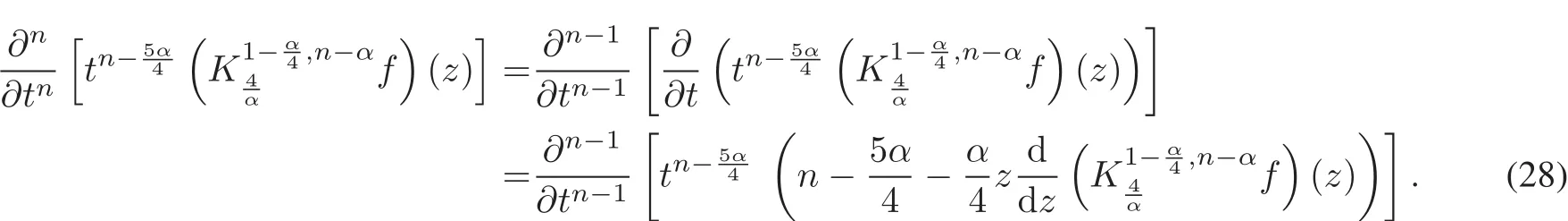
Continuously,we have

Considering the fractionaldifferentialoperator of Erd´elyi-Kober fractionaloperatorof(22),we get

Therefore,it’s fascinating thatEq.(1)reduces to the fractional-orderODE

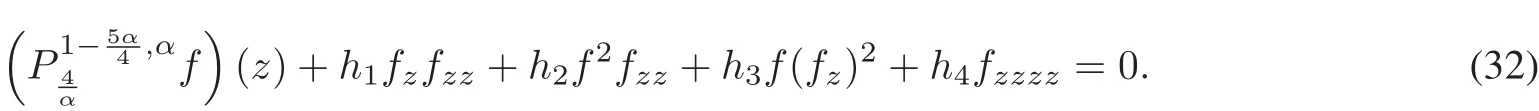
4 Conservation laws

4.1 Preliminaries of conservation laws

According to the Riemann-Liouville left-sided time-fractionalderivative[35−37],we have

in Eq.(1),where Dtis the operatorconcerning t ofdifferentiation,n=[α]+1.In addition,the definitionu is given as follows.

Definition 3[22]The left-sided time-fractionalintegraloforderu is defined by

where,Γ(z)is the Gamma function.

Definition 4 A conserved vectoris said to obey the conservation law,ifitsatisfies the following conservation equation

Firstly,we suppose thatEq.(1)has the following formalLagrangian

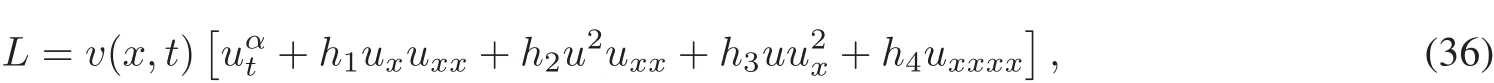
where,v(x,t)is a new dependentvariable.In view ofthe previous Lagrangian,we getan action integralas follows

Similar to the case of integer-order nonlinear differential equations[30−31],the adjoint equation is available. Therefore,we getthe conclusion thatthe Euler-Lagrange equation of nonlinear fourth-order evolution equation Eq. (1)with adjointequation in the following

and the definition ofthe Euler-Lagrange operatoris obtained as below.

Definition 5[30−31]The Euler-Lagrange operatoris defined by

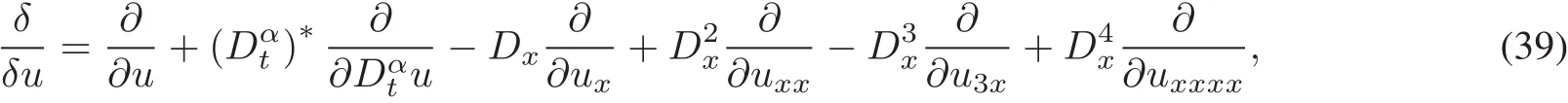
For the Riemann-Liouville differentialoperators

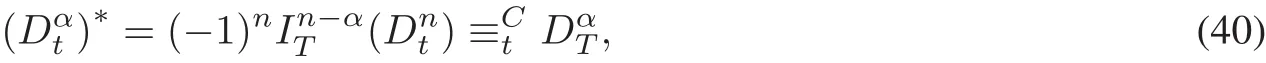
We find that Eq.(1.1)with the Riemann-Liouville fractional derivative satisfies the conservation equation of Eq.(33)as follows

when,h3=2h2.

In case oftwo independentvariables t,x,and one dependentvariable u(x,t),we get

where l is the identity operator,shows the Euler-Lagrange operator,and the Noether operators are provided by Nt,Nxrespectively.In addition,X is defined by

Applying the Riemann-Liouville time-fractional derivative to Eq.(1),we obtain the following operator Ntdefined in[30–31]

where J is the integral,

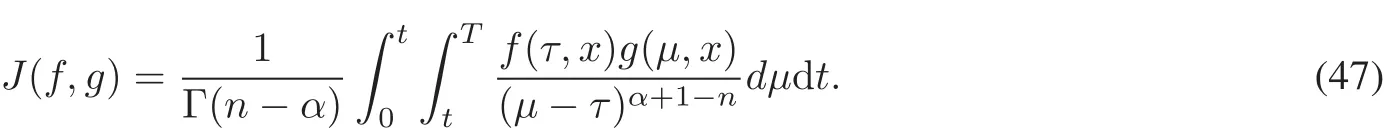
The operator Nxis defined by

No matterwhatthe solutions and generator X of Eq.(1)are,we obtain

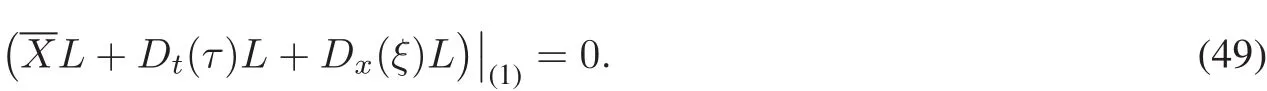
Itis easy to find thatEuler-Lagrange(38)ofEq.(1)is equalto zero.Hence,the conservation law resulted ftom the right-hand side of the equality is given by[30]

Comparing(35)and(50),we find thatthe following components ofconserved vectors is always valid obviously

4.2 Conservation laws of time fractionalfoam drainage equation

In this section,the conservation laws of Eq.(1)is available.

Theorem 3 The components of conserved vectors aboutfourth-orderevolution equation is given by the following two cases

Case 1 whenα∈(0,1)

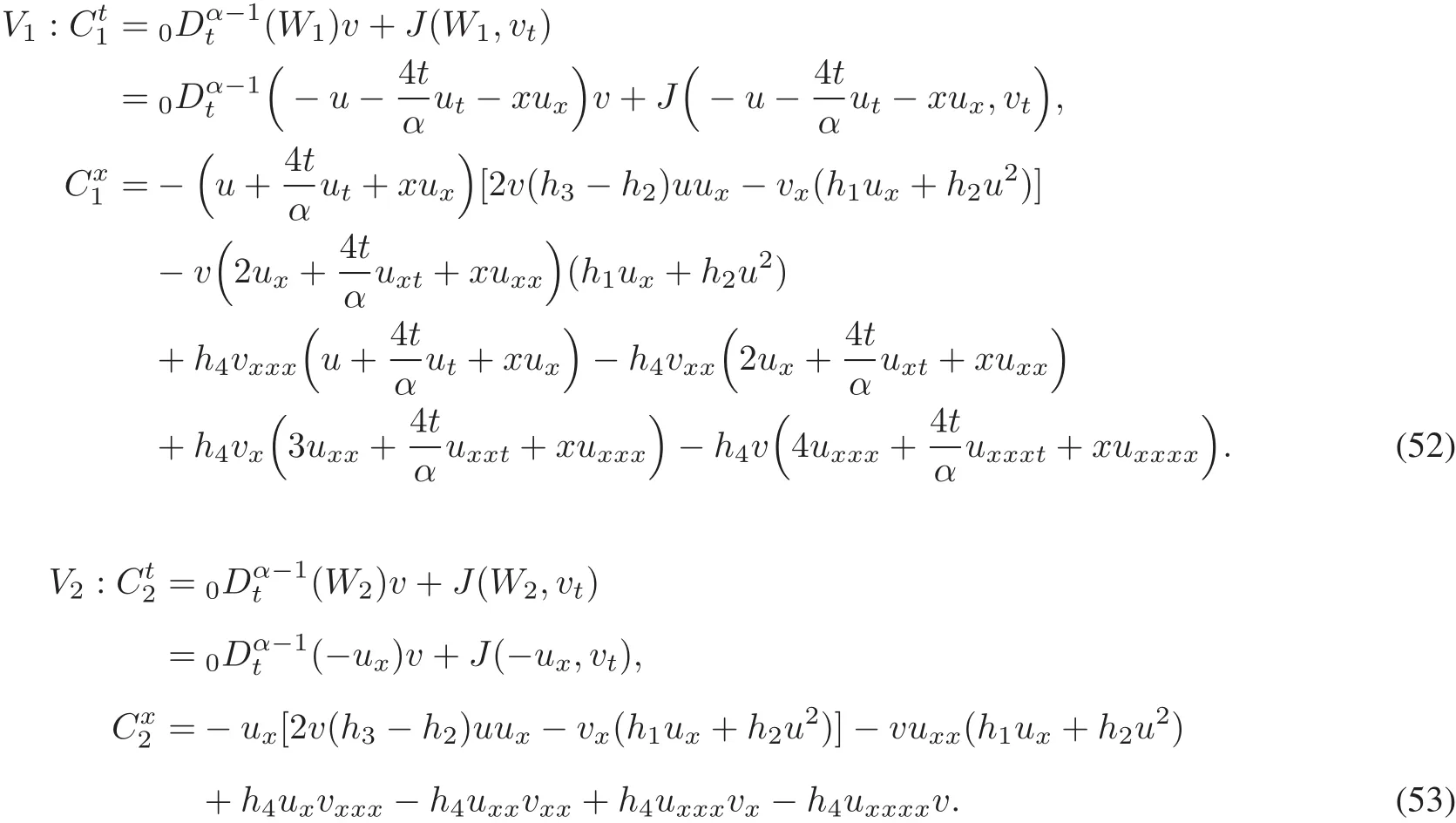
Case 2 whenα∈(1,2)

where the functions of Wi,i=1,2 have the form

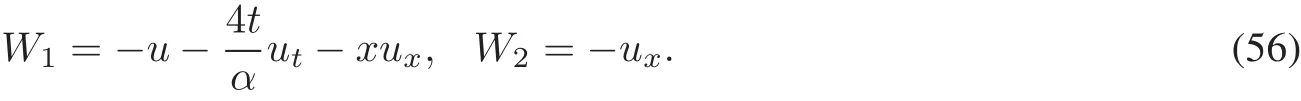
Proof Substituting(46)and(48)into Eq.(1),we getthe conserved vectoras below.

For the case ofα∈(0,1),

In accordance with the fractionalgeneralizations of the Riemann-Liouville differentialoperators[30],we have the specific form ofthe time fractionalfourth-orderevolution equationa as follows.Whenα∈(0,1),we substitute (36)along with(56)into(57)and(58).Whenα∈(1,2),we substitute(36)and(56)into(59)and(60),and see that Theorem 3 is 1.00,0.00,0.00.The proof is completed.

5 Conclusions and discussions

In this paper,we study the time fractional nonlinear fourth-order evolution equation by way of Lie symmetry.Based on known results,we conclude the corresponding vector fields.In addition,these corresponding vector fields are further applied in order to constructthe symmetry reductions of∂+h1uxuxx+++

h4uxxxx,0＜α≤2.In the end,we obtain the conservation laws.However,we still have a lot of problems to research,such as how can we study the time-space fractionalequation?How to solve the fractionaldifferential equations with more independentand dependentvariables?These are ourfuture work.

[1]Bluman G W,Anco S.Symmetry and integration methods for differential equations[M].New York:Springer-Verlag, 2002.

[2]Ibragimov N H.CRC handbook of Lie group analysis ofdifferentialequations:Symmetries,exactsolutions and conservation laws[M].New York:CRC Press,1994.

[3]Lakshmanan M,Kaliappan P.Lie transformations,nonlinear evolution equations,and Painlev´e forms[J].Journalof mathematicalphysics,1983,24(4):795–806.

[4]Olver P J.Applications of Lie groups to differentialequations[M].New York:Springer-Verlag,1986.

[5]Ovsiannikov L V.Group analysis of differentialequations[M].Ames WF,Transl.New York:Academic Press,1982.

[6]Tian S F.The mixed coupled nonlinear Schr¨odinger equation on the half-line via the Fokas method[J].Proceedings of the RoyalSociety A:MathematicalPhysicaland Engineering Sciences,2016,472:20160588.

[7]Wang D S,Yin Y B.Symmetry analysis and reductions ofthe two-dimensionalgeneralized Benney system via geometric approach[J].Computers&Mathematics with Applications 2016,71:748-757.

[8]Wang D S,Wei X Q.Integrability and exactsolutions of a two-component Korteweg-de Vries system[J].Applied Mathematics Letters 2016,51:60-67.

[9]Tian S F,Zhang H Q.On the integrability ofa generalized variable-coefficientKadomtsev-Petviashviliequation[J].Journal of Physics A:Mathematicaland Theoretical2012,45(5):055203(29pp).

[10]Tian S F,Zhang Y F,Feng B L,et al.On the Lie algebras,generalized symmetries and darboux transformations of the fifth-orderevolution equations in shallow water[J].Chinese Annals of Mathematics,Series B,2015,36(4):543-560.

[11]Tian S F.Initial-boundary value problems for the generalcoupled nonlinear Schr¨odinger equation on the intervalvia the Fokas method[J].Journalof Differential Equations 2017,262(1):506-558.

[12]Tian S F,Zhang H Q.On the integrability of a generalized variable-coefficientforced Korteweg-de Vries equation in fluids [J].Studies in Applied Mathematics 2014,132(3):212-246.

[13]Diethelm K.The analysis of fractionaldifferentialequations[M].New Nork:Springer dordrechtheidelberg,2010.

[14]Liang YJ,Chen W.Asurvey on computing L´e vy stable distributions and a new matlab toolbox[J].SignalProcessing,2013, 93(1):242-251.

[15]Hu S,Chen W,Gou X F.Modalanalysis of fractionalderivative damping modeloffrequency-dependentviscoelastic soft matter[J].Advances in Vibration Engineering,2011,10:187-196.

[16]El-Sayed A M A,Gaber M.The Adomian decomposition method for solving partialdifferentialequations of fractalorder in finite domains[J].Physics Letters A,2006,359(3):175-182.

[17]Gazizov R K,Kasatkin A A,Lukashchuk S Y.Continuous transformation groups of fractionaldifferentialequations[J]. Vestnik USATU,2007,9(3):21.

[18]Gazizov R K,Kasatkin A A,Lukashchuk S Y.Symmetry properties of fractionaldiffusion equations[J].Physica Scripta, 2009(T136):014016.

[19]Sahadevan R,Bakkyaraj T.Invariantanalysis oftime fractionalgeneralized Burgers and Korteweg-de Vries equations[J]. Journalof mathematicalanalysis and applications,2012,393(2):341-343.

[20]Wang G W,Xu T Z.Invariant analysis and exact solutions of nonlinear time fractional Sharma-Tasso-Olver equation by Lie group analysis[J].Nonlinear Dynamics,2014,76:571-580.

[21]Huang Q,Zhdanov R.Symmetries and exactsolutions ofthe time fractional Harry-Dym equation with Riemann-Liouville derivative[J].Physic A,2014,409:110-118.

[22]Lukashchuk S Y,Makunin A V.Group classification ofnonlinear time-fractionaldiffusion equation with a source term[J]. Applied Mathematics and Computation,2015,257:335-343.

[23]Noether E.Invariantvariationa problems[J].Transport Theory and Statistical Physics,1971,1(3):183-207.

[24]Frederico G S F,Torres D F M.A formulation of Noethers theorem for fractionalproblems of the calculus of variations [J].Journalof MathematicalAnalysis and Applications.2007,334(2):834-846.

[25]Atanackovic T M,Konjik S,Pilipovic S,etal.Variationalproblems with fractionalderivatives:invariance conditions and N¨others theorem[J].Nonlinear Analysis,2009,(5-6):1504-1517.

[26]Malinowska A B.A formulation of the fractional Noether-type theorem for multidimensional Lagrangians[J].Applied Mathematics Letters,2012,25(11):1941-1946.

[27]Odzijewicz T,Malinowska A B,Torres D F M.Noethers theorem forfractionalvariationalproblems of variable ordern[J]. Central European Journalof Physics,2013,11(6):691-701.

[28]Bourdin L,Cresson J,Greff I.A continuous/discrete fractional Noethers theorem[J].Communications in Nonlinear Science and NumericalSimulation,2013,18(4):878-887.

[29]Ibragimov N H.A new conservation theorem[J].Journal of Mathematical Analysis and Applications,2007,333(1):311-328.

[30]Lukashchuk S Y.Conservation laws for time-fractionalsubdiffusion and diffusion-wave equations[J].Nonlinear Dynamics,2015,80(1):791-802.

[31]Gazizov R K,Ibragimov N H,Lukashchuk S Y.Nonlinear self-adjointness,conservation laws and exact solutions of time-fractional Kompaneets equations[J].Communications in Nonlinear Science and Numerical Simulation,2015,23(1-3):153-163.

[32]Nikolai A K,Maria V D.Polygons of differential equations for finding exact solutions[J].Chaos,Solitons and Fractals, 2007,33(5):1480-1496.

[33]Ibragimov N H.Transformation groups applied to mathematicalphysics[M].New York:Springer-Verlag,1985.

[34]Kiryakova V S.Generalised fractionalcalculus and applications[M].New York:CRC Press,1993.

[35]Baleanu D,Diethelm K,Scalas E,et al.Fractional calculus:Models and numerical methods[M].Singapore:World Scientific Publishing Company,2012.

[36]Samko S,Kilbas A,Marichev O.Fractionalintegrals and derivatives:Theory and applications[M].London:Gordon and Breach,1993.

[37]Kilbas A A A,Srivastava H M,Trujillo J J.Theory and applications of fractionaldifferentialequations[M].Amsterdam: Elsevier Science Limited,2006.

O 175.12 Documentcode:A Article ID:1000-5137(2017)03-0363-12

10.3969/J.ISSN.100-5137.2017.03.004

date:2016-09-12

This research was supported by the National Training Programs of Innovation and Entrepreneurship for Undergraduates(201410290039);the Fundamental Research Funds for the Central Universities(2015QNA53,2015XKQY14); the General Financial Grant from the China Postdoctoral Science Foundations(2015M570498 and 2017T100413);Natural Sciences Foundation of China(11301527).

∗Corresponding author:Tian Shoufu,associate professor,reseach area:partial differential equation.E-mail:sftian@cumt.edu.cn,shoufu 2006@126.com;Song Xiaoqiu,professor,reseach area:functional analysis.E-mail:songxiaoqiu@cumt.edu.cn