The controllability ofnonlinear fractionaldamped dynamicalsystems with controldelay

Xu Zhongyang,Xie Feng(College of Science,Donghua University,Shanghai201620,China)

The controllability ofnonlinear fractionaldamped dynamicalsystems with controldelay

Xu Zhongyang,Xie Feng∗
(College of Science,Donghua University,Shanghai201620,China)

This paper deals with the controllability of nonlinear fractionaldamped dynamicalsystem with controldelay which involvesfractionalCaputo derivatives.Using fixed pointtheorem,we establish sufficientconditionsforthe controllability ofnonlinearfractionaldamped dynamicalsystem with control delay are established.These conditions are easily checked.Two examplesare given to illustrate the main results.

controllability;fractionaldamped systems;controldelay

2010 MSC:34A08,70J25,93D20

1 Introduction

The fractionaldifferentialequations have gained considerable attention in the pastfour decades,which play an important role in physics,chemistry and engineering,see,for instance,[1–5].Controllability is a fundamental concept in control theory.Recently,the controllability of fractional differential equations have been extensivelystudied,and many results are obtained[6−8].Notice thattime delay is a common phenomenon in practicalsystems, many researchershave paid much attention and have also achieved many greataccomplishments[10−11].

A remarkable feature forcontroldelay systems is thatthe future evolution ofthe systems depends notonly on the presentcontrolstate,butalso on a period of controlhistory.

In[12],Sebakhy and Bayoumi explored a simplified criterion for the controllability of linear systems with delay in control.In[13],Chyung obtained a necessary and sufficientcondition forthe controllability oflineartimeinvariantsystems with a time delay.

Balachandran,Zhou,Tuujillo and Kokila studied the relative controllability of severalkinds of fractionaldynamicalsystems with delays in[14–16].

The fractionaldamped system is investigated in[9],where the controllability oflinear and nonlinearfractional damped dynamical systems are explored.In[17],He,Zhou and Kou investigated the linear fractional damped dynamicalsystem with time delay in control

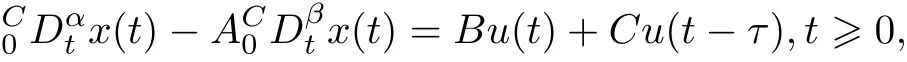
Motivated mainly by[9,17],we concern with,in this paper,the controllability of the following nonlinear fractionaldamped dynamicalsystem with delays in control:

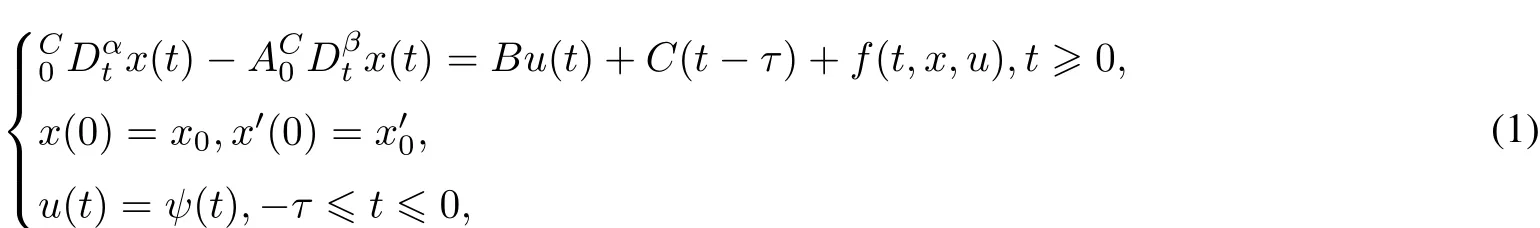
The Caputo fractionalderivative of orderα(0≤m≤α＜m+1)for a function f:R+→R is defined by

The Mittag-Lefflerfunction Eα(z)withα＞0 is defined by

The two-parameterMittag-Lefflerfunction Eα,β(z)α,β＞0 is defined by

Definition 1 The set y(t)={x(t),x′(t),ut}is the complete state of the system(1)attime t.

Definition 2 The system(1)is said to be controllable on J=[0,T],if,for each complete state y(0)and for each vector x1∈Rn,there exists a control u∈C(J)such thatthe corresponding solution of(1)with x(0)= x0=satisfies x(T)=x1.

In this definition ofcontrollability,we are concerned in steering only the states butnotthe velocity vector x′0in (1).

Lemma 1[9]The generalsolution of system

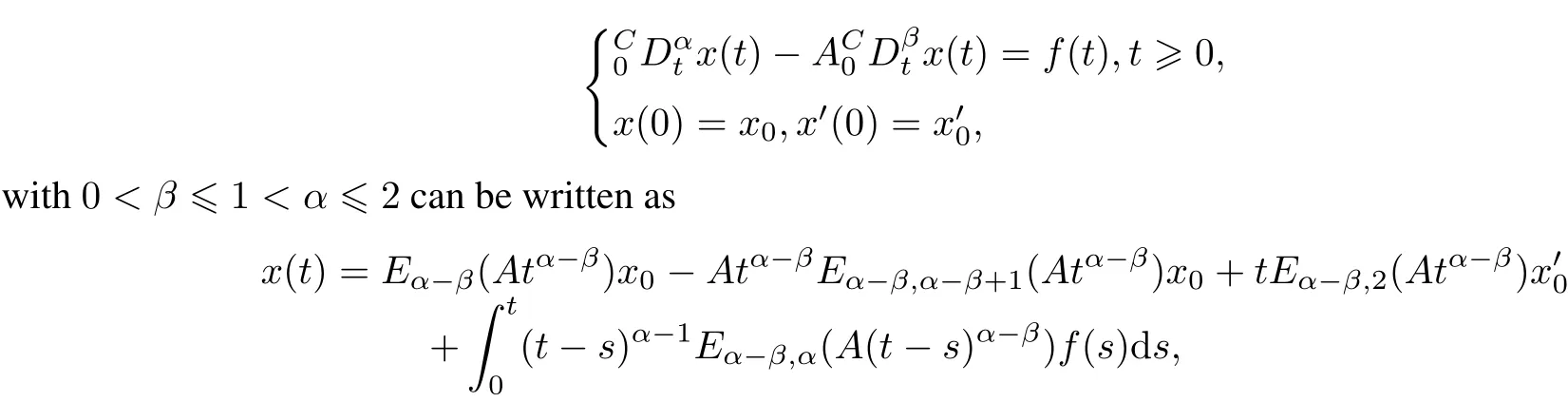
where f:J→Rnis a continuous function.

For linear system

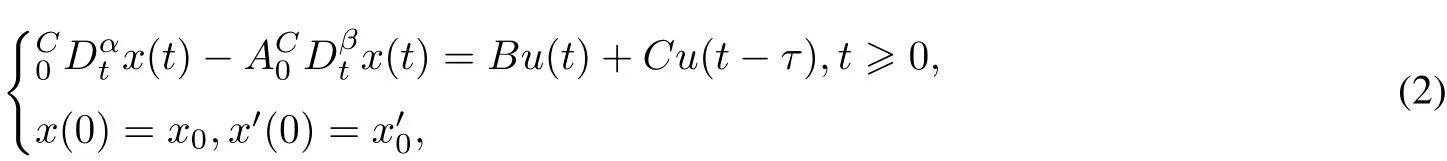
we have the following lemmas.

Lemma 2[17]The linear fractionaldamped dynamicalsystem with controldelay(2)is controllable if and only ifthe controllability Grammian matrix defined by

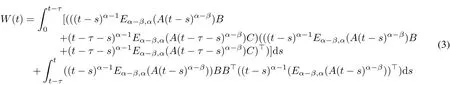
is invertible.

Lemma 3[17]The linear fractional damped dynamical system with control delay(2)is controllable if and only if

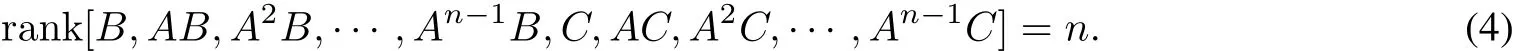
2 Main Results

In this section,we state and prove our main results.

Denote

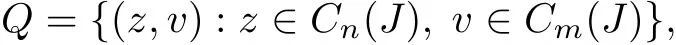
with the uniform norm‖(z,v)‖=‖z‖+‖v‖=z(t)|+|v(t)|,where Cn(J)={f:J→|f is continuous on J},Cm(J)={f:J→|f is continuous on J}are Banach spaces.We denote the max norms inRnand Rmby|·|nand|·|m,and use the notation|·|if there is no confusion.For each(z,v)∈Q,consider the following nonlinearfractionaldamped dynamicalsystem:

By Lemma 1,the solution ofthe system(5)can be written as

Forbrevity,letus introduce the following notations and constants:

We also define

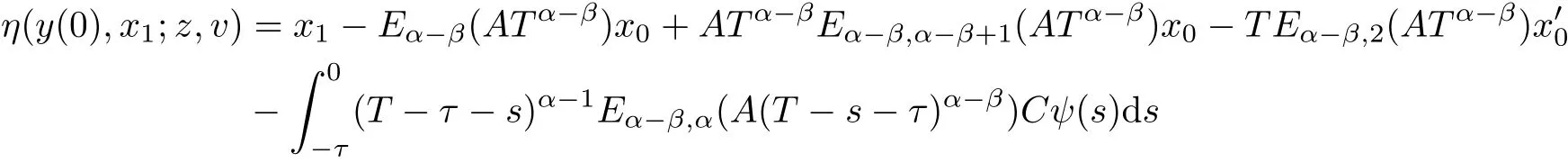
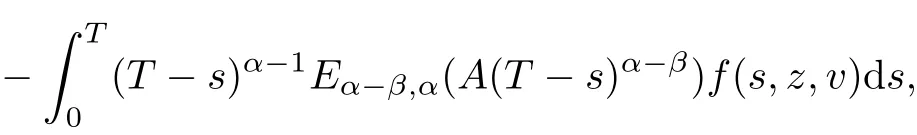
and define the controlfunction

where the complete state y(0)and the vector x1∈Rnare chosen arbitrarily.

In orderto prove our main result,we need the following lemma.

Lemma 4[18]Suppose the function f is bounded locally inνand satisfies that

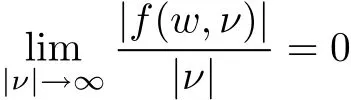
uniformly in w∈J.Then forevery pairof constants c,d,there is a constant r such thatif|ν|≤r,then c|f(w,ν)|+ d≤r forall w∈J.

Theorem 1 Suppose thatthe continuous function f satisfies the condition

uniformly in t∈J,and the linearfractionalsystem(2)is controllable.Then the nonlinearsystem(1)is controllable on J.

Proof By hypothesis,system(2)is controllable.Itfollows from Lemma 2 that W given by(3)is invertible. We define the operatorΨ:Q→Q as follow:

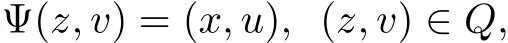
where u(t)is given by(8),and

Now,we show thatthere exists a constant r＞0 such that

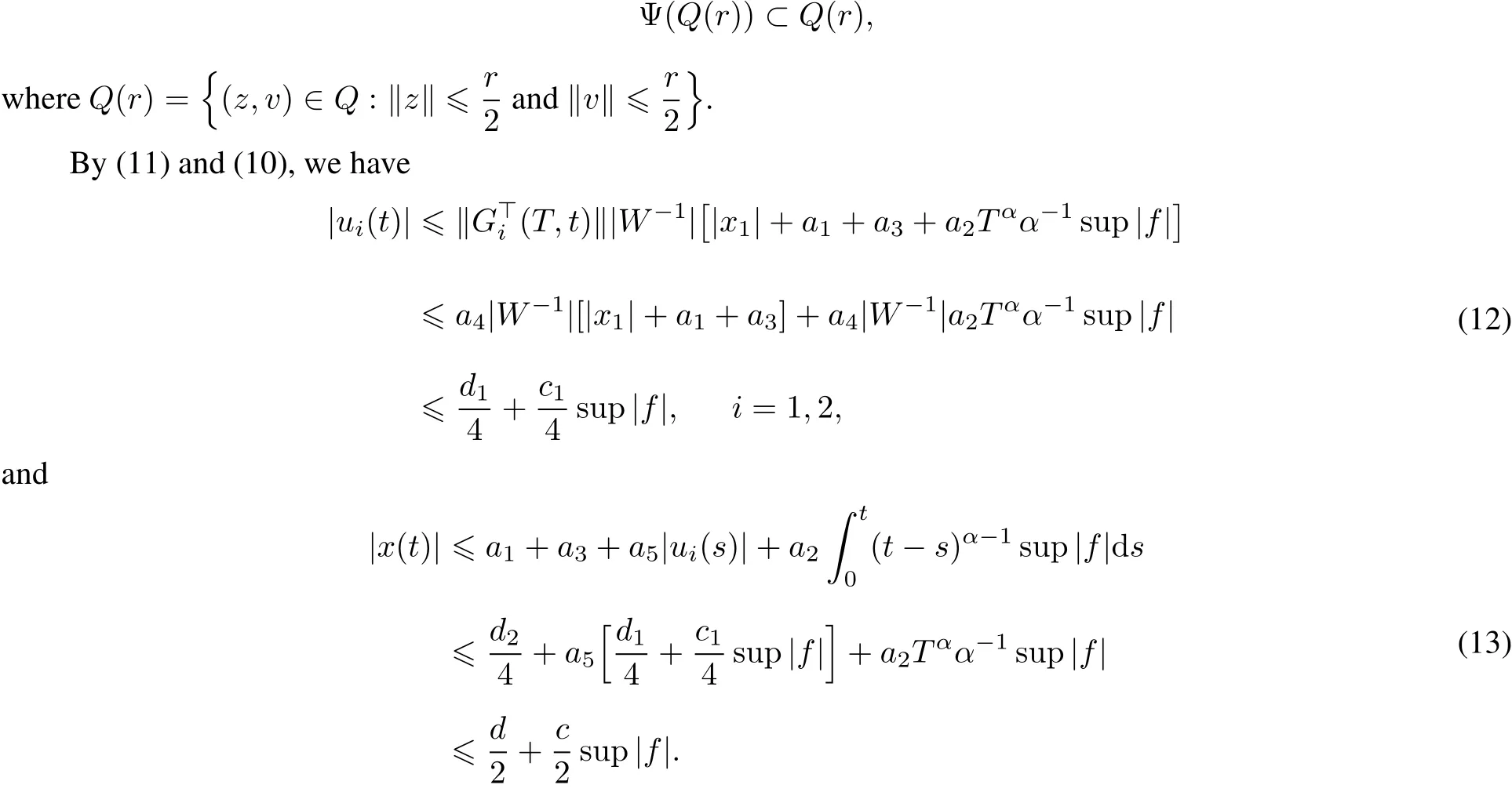
Since the function f satisfies(9),by Lemma 4,for each pair of positive constants c and d,there exists a positive constant r such that,if|(z,v)|≤r,then

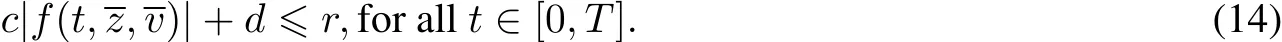
Now we take c,d as given by(7),and choose r such that(14)holds.Therefore,if‖z‖≤and‖v‖≤,then|z(s)|+|v(s)|≤r for all s∈[0,T].Itfollows that d+c sup|f|≤r.Therefore,by(12),we have|u(s)|≤ for all s∈[0,T],and hence‖u‖≤by(13),‖x‖≤.Thus,Ψ(Q(r))⊂Q(r).

Next,we show thatΨhas a fixed pointin Q(r).Actually,the continuity of f implies thatthe operatorΨis continuous.By Arzela-Ascolitheorem,we have thatthe operatorΨis completely continuous.Since Q(r)is closed, bounded and convex,itfollowsfrom the Schauderfixed pointtheorem thatΨadmitsa fixed point(z,v)∈Q(r)such thatΨ(z,v)=(z,v)≡(x,u).Hence x(t)is the solution ofthe system(1),and itis easy to verify that x(T)=x1, this means that the control function u(t)steers the system(1)from complete state y(0)to x1on[0,T].Thus the system(1)is controllable on[0,T].

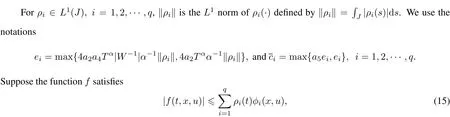
whereφi:×Rm→R+are measurable functions andρi:J→R+are L1functions for i=1,2,···,q.

Theorem 2 Suppose thatthe linear system(2)is controllable and the following condition holds

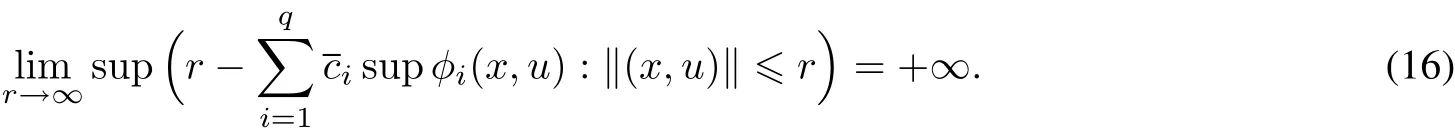
Then the nonlinearfractionaldamped system(1)is controllable on J.

Proof Define the operatorΦ:Q→Q byΦ(z,v)=(x,u)where x and u are as defined in(10)and(11).Now let

By(16),there exists r0＞0 such that

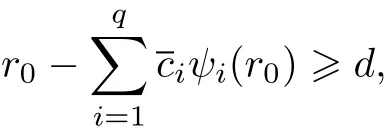
where d is defined in(7).This implies that

Then,by(11)and(10),we have

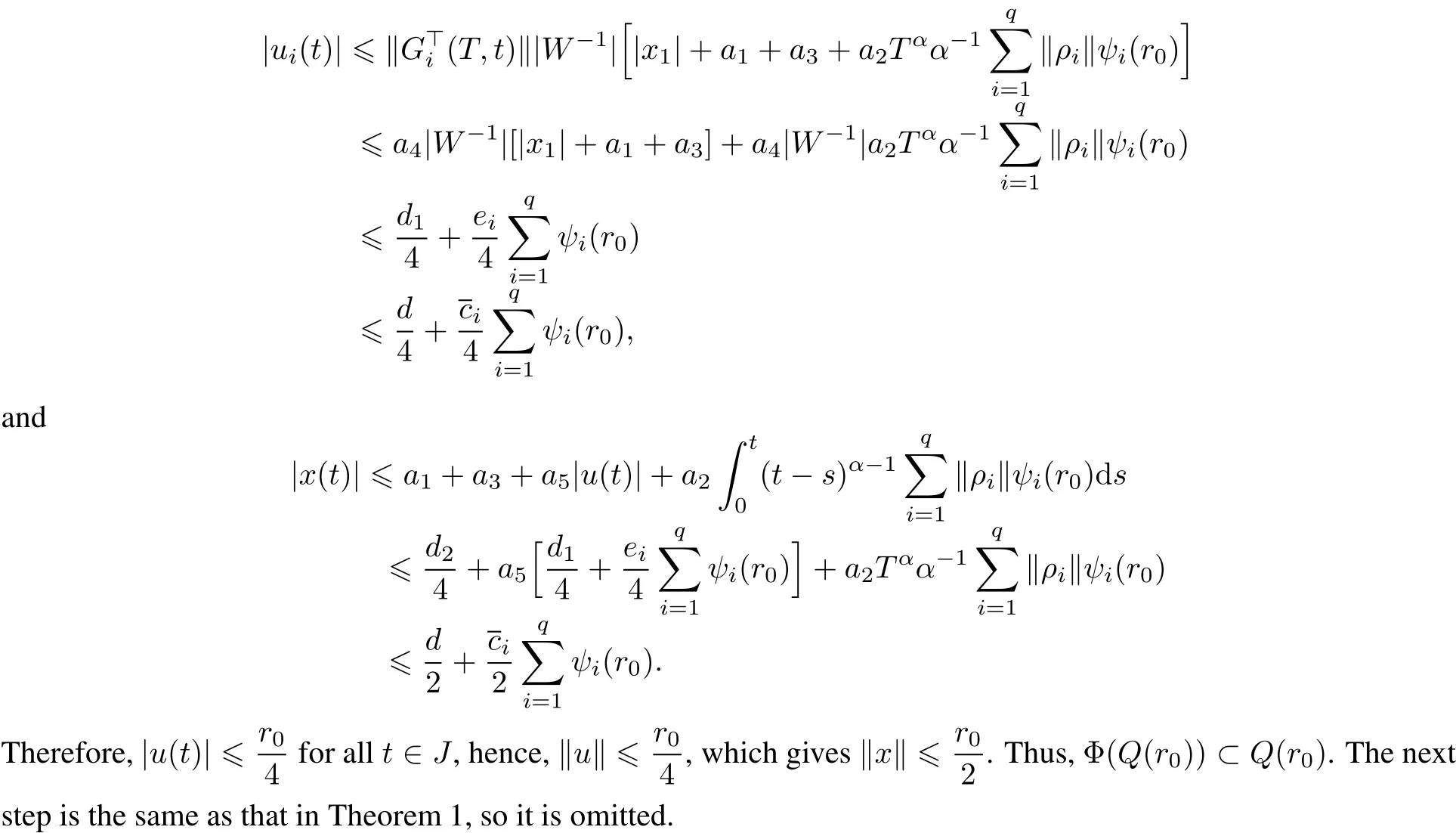
3 Examples

In this section we apply the results obtained in the previous sections for the following fractionaldamped dynamicalsystems with delays in control.

Example 1 Consider the fractionaldamped nonlinearsystem with controldelay

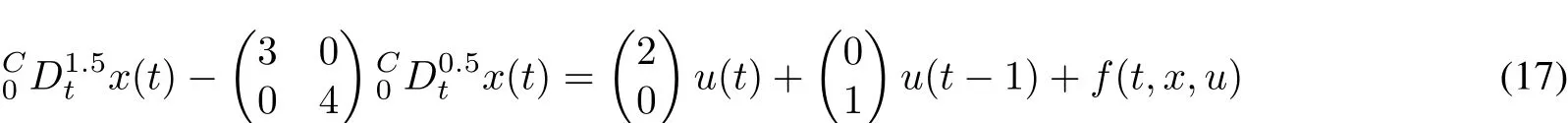
where f(t,x,u)is given by

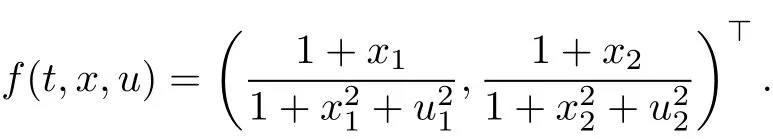
where x,u∈R2.A simple computation shows that

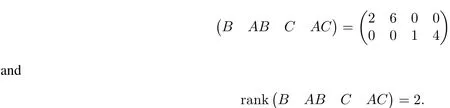
From Lemma 3,we know thatthe corresponding linear system of(17)is controllable.

We see that f(t,x,u)is continuous and satisfies the condition(9),and thus the fractionaldamped system(17) is controllable.

Example 2 Considerthe nonlinearsystem

whereα=1.5,β=0.5,

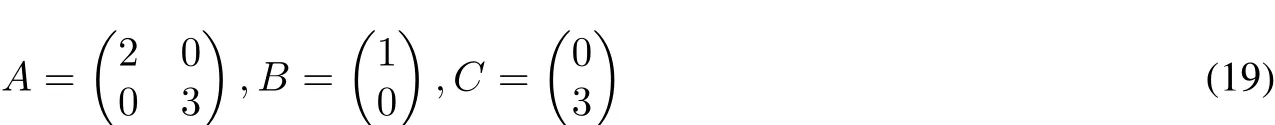
and f(t,x,u)is given by

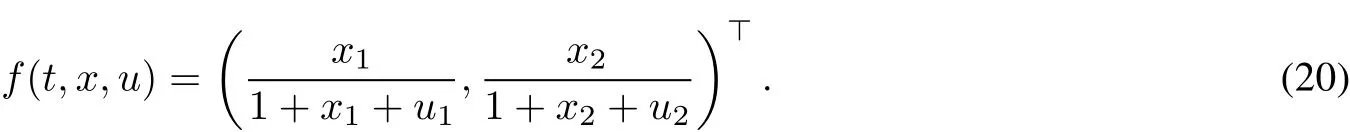
where x,u∈R2.A simple computation shows that

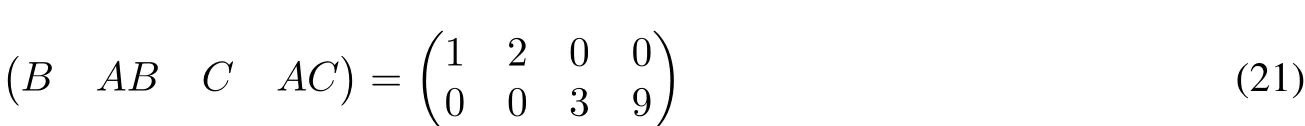
and

From Lemma 3,we know thatthe linearsystem is controllable.Furthermore,

In orderto prove the required results,itis enough to show the condition(16)holds under the following settings:

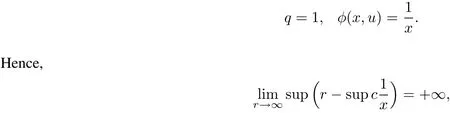
and thus the fractionaldamped system(18)is controllable on[0,T].

References:

[1]Hilfer R.Applications offractionalcalculus in physics[M].Singapure:World Scientific Publisher,2000.

[2]Kilbas A A,Srivastava H M,Trujillo J J.Theory and applications of fractional differential equations[M].Amsterdam: Elsevier,2006.

[3]V.Lakshmikantham V,Leela S,Vasundhara J.Theory of fractionaldynamic systems[M].Cambridge:Cambridge Academic Publishers,2009.

[4]Miller K S,Ross B.An introduction to the fractionalcalculus and fractionaldifferentialequation[M].New York:Wiley, 1993.

[5]Podlubny I.Fractionaldifferentialequations[M].New York:Academic Press,1998.

[6]Balachandran K,Dauer J P.Controllability of nonlinear systems in Banach spaces:A survey[J].J Optim Theory Appl, 2002,115:7-28.

[7]Balachandran K,Park J Y.Controllability of fractionalintegrodifferential systems in Banach spaces[J].Nonlinear Anal Hybrid Syst,2009,3:363-367.

[8]Debbouche A,Torres D F M.Approximate controllability of fractional delay dynamic inclusions with nonlocalcontrol conditions[J].ApplMath Comput,2014,243:161-175.

[9]Balachandran K,Govindaraj V,Rivero M,et al.Controllability of fractionaldamped dynamicalsystems[J].Appl Math Comput,2015,257:66-73.

[10]Gu K Q,Kharitonov L V,Chen J.Stability oftime-delay systems[M].Basel:Birkhauser,2003.

[11]John C,Loiseau J J.Applications of time delay systems[M].Berlin Heidelberg:Springer-Verlag,2007.

[12]Sebakhy O,Bayoumi M M.A simplified criterion for the controllability of linear systems with delay in control[J].IEEE Trans Automatic Control,1971,16:364-365.

[13]Chyung D H.On the controllability of linear systems with delay in control[J].IEEE Trans Automatic Control,1970, 15:55-257.

[14]Balachandran K,Zhou Y,Trujillo,J J.Relative controllability of fractional dynamical systems with multiple delays in control[J].ComputMath Appl,2012,64:3037-3045.

[15]Balachandran K,Zhou Y,Kokila J.Relative controllability of fractional dynamical systems with distributed delays in control[J].ComputMath Appl,2012,64:3201-3209.

[16]Balachandran K,Zhou Y,Kokila J.Relative controllability of fractional dynamical systems with delays in control[J]. Commun Nonlinear SciNumer Simul,2012,17:3508-3520.

[17]He B B,Zhou H C,Kou C H.The controllability offractionaldamped dynamicalsystems with controldelay[J].Commun Nonlinear SciNumer Simulat,2016,32:190-198.

[18]Dauer JP.Nonlinear perturbations ofquasi-linearcontrolsystems[J].JApplied Math Appl,1976,54:717-725.

O 175.13 Document code:A Article ID:1000-5137(2017)03-0375-09

10.3969/J.ISSN.100-5137.2017.03.005

date:2016-07-08

This work is partially supported by the Natural Science Foundation of Shanghai(15ZR1400800).

∗Corresponding author:Xie Feng,professor,reaseach area:ordinary differentialequations,E-mail:fxie@dhu.edu.cn