Two-intervaleven order differentialoperators in directsum spaces with inner productmultiples

Suo Jianqing,Wang Wanyi(1.Schoolof Mathematical Sciences,Inner Mongolia University,Hohhot01001,China; .College of Science,Inner Mongolia Agricultural University,Hohhot010019,China)

Two-intervaleven order differentialoperators in directsum spaces with inner productmultiples

Suo Jianqing1∗,Wang Wanyi2
(1.Schoolof Mathematical Sciences,Inner Mongolia University,Hohhot010021,China; 2.College of Science,Inner Mongolia Agricultural University,Hohhot010019,China)

We study two-intervalsingulardifferentialequationsand show thattheirself-adjointoperator realizations in directsum Hilbertspaces can be enlarged by using inner productmultiples.

self-adjoint;interface conditions;transmission conditions

2010 MSC:34B24,34L99,47E05

1 Introduction

Partly motivated by applications,in particular(see[1–2]),Everittand Zettlin[3]developed a theory of selfadjointrealizations of Sturm-Liouville problemson two intervals in the directsum of Hilbertspaces associated with these intervals.See Chapter 13 in[4]for an exposition of this theory.This theory was extended in[5]to higher orderregularand singularequationsand any numberofintervals,finite orinfinite.

As in the one intervalcase the characterization of[5]depends on maximaldomain vectors.These vectors depend on the coefficients of each differential equation and this dependence is implicit and complicated.In[6]Wang,Sun and Zettlgive an explicitcharacterization of allself-adjointdomains in terms of certain solutions for real λfor the one intervalcase when one endpointis regular and the other is singular.In analogy with the celebrated Weyllimit-point(LP),limit-circle(LC)theory in the second order case,they construct LC and LP solutions and characterize the self-adjointdomains in terms of the LC solutions.Following[6],Hao,Wang,Sun and Zettlgive a new characterization by dividing(a1,b1)into two intervals(a1,c1)and(c1,b1)forsome c1∈(a1,b1)and by using the LC solutions on each intervalconstructed in[6]when a1and b1are singular in[7].In[8],Suo and Wang extend the characterization in[7]to two-intervalcase butthe resultreduces to the case when one or two or three or four endpoints are regular.

As noted in[3],a simple way of getting self-adjointoperators in a directsum Hilbertspace is to take the directsum ofself-adjointoperators from each of the separate Hilbertspaces.However,there are many self-adjoint operators which are notmerely the sum of self-adjointoperators from each of the separate intervals.These“new”self-adjointoperators involve interactions between the two intervals.Therefore in[3]the authors develop a“twointerval”theory.Mukhtarov and Yakubov[9]observe that the set of two-interval self-adjoint realizations can be significantly enlarged by using differentmultiples of the usualinner products associated with each of the intervals. In[10]and[11],Sun,Wang and Zettl use the Mukhtarov-Yakubov modification of the Everitt-Zettl theory to characterize allself-adjointrealizationsofregularand singulartwo-intervalSturm-Liouvilleproblemsrespectively in the modified directsum Hilbertspace with differentinner productmultiples.They generate self-adjointrealizations for the second order case with coupled boundary conditions and a real coupling matrix K,the method of[3] requires that det(K)=1 whereas with the Mukhtarov-Yakubov modification in[10]and[11]itis only required that det(K)is positive.In[12],Suo and Wang use the Mukhtarov-Yakubov modification to characterize all selfadjointrealizations of two-intervaleven order problems with one endpointof each interval(a1,b1),(a2,b2)regular using Hilbert spaces but with the usual inner products replaced by appropriate multiples.The interplay of these multiples with the boundary conditions generates self-adjointproblems of even orderwith realcoupling matrices K which are much more generalthan the coupling matrices from the′′unmodified′′theory.

In this paper we characterize all self-adjoint realizations for singular two-interval even order problems in the modified directsum Hilbertspace with differentinnerproductmultiples.As in[12],the interplay ofthese multiples with the boundary conditions generates self-adjointproblems with realcoupling matrices K which are much more generalthan the coupling matrices from the′′unmodified′′theory.Our resultreduces to the case when one or two or three orfourendpointsare regular.Thus the results given in[8]are specialcases ofourresults and can be obtained simply by taking both ofthe multiple innerproductparameters to be unity,and the results given in[12]are special cases of our results and can be obtained when one endpointof each interval(a1,b1),(a2,b2)is regular.We give a numberofexamples to illustrate this additionalgenerality,among otherthings.

From anotherperspective,instead ofusing multiples ofthe usualinnerproducts,ourapproach can be described as using multiples ofweightfunctions.

2 Notation and basic facts for one interval

Although we only consider even order equations with realcoefficients in this paper,we summarize some basic facts about general quasi-differential equations of even and odd orders and real or complex coefficients for the convenience ofthe reader.

Let J=(a,b)be an intervalwith−∞≤a＜b≤∞and let n be a positive integer(even or odd).For a givenset S,Mn(S)denotes the setof n×n complex matrices with entries from S. Let

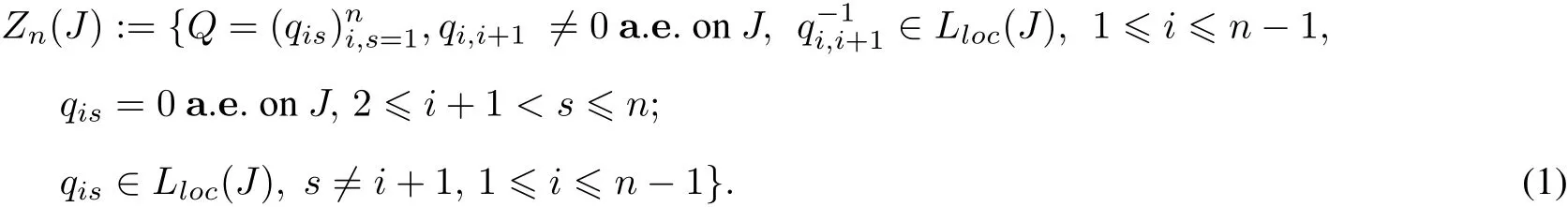
Let Q∈Zn(J).We define

where qn,n+1:=1,and ACloc(J)denotes the setof complex valued functions which are absolutely continuous on allcompactsubintervalsof J.Finally we set

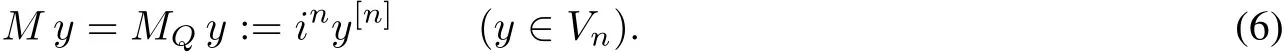
The expression M=MQis called the quasi-differentialexpression associated with Q.For Vnwe also use the notations V(M)and D(Q).The function(0≤i≤n)is called the i-th quasi-derivative of y.Since the quasi-derivative depends on Q,we sometimes writeinstead of y[i].

Remark 2.1 The operator M:D(Q)→Lloc(J)is linear.

Let Zn(J,R)denote the matrices Q∈Zn(J)which have realvalued components.

Definition 2.1 Let Q∈Zn(J,R)and let M=MQbe defined as above.Assume that

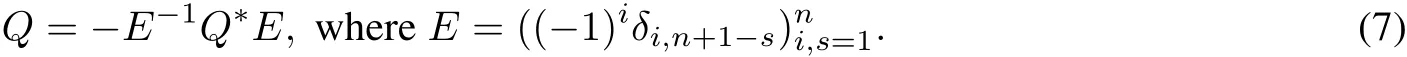
Then M=MQis called a symmetric differentialexpression.

Let w∈Lloc(J)be positive a.e.on J.We considerthe Hilbertspace

The maximaland minimaloperators associated with a symmetric expression Q and a positive weightfunction w in the Hilbertspace H are defined as follows.

Definition 2.2 Assume Q∈Zn(J,R)satisfies(7)and let M=MQbe the associated symmetric expression. Let w∈Lloc(J)be positive a.e.on J.Define

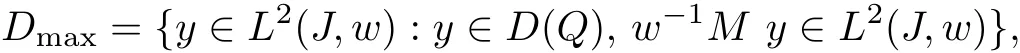
Lemma 2.1 Let Sminand Smaxbe defined as above.Then Dminand Dmaxare dense in H,Sminand Smaxare closed operators in H,==nd Sminis a symmetric operatorin H.

From Definition 2.2 and Lemma 2.1 we see that every self-adjoint extension S of the minimal operator is‘between’the minimaland maximaloperators,i.e.,we have

Thus these self-adjointoperators S are distinguished from one another only by their domains.

Lemma 2.2[Lagrange Identity]Assume Q∈Zn(J,R)satisfies(7)and let M=MQbe the corresponding differentialexpression.Then for any y,z∈D(Q)we have

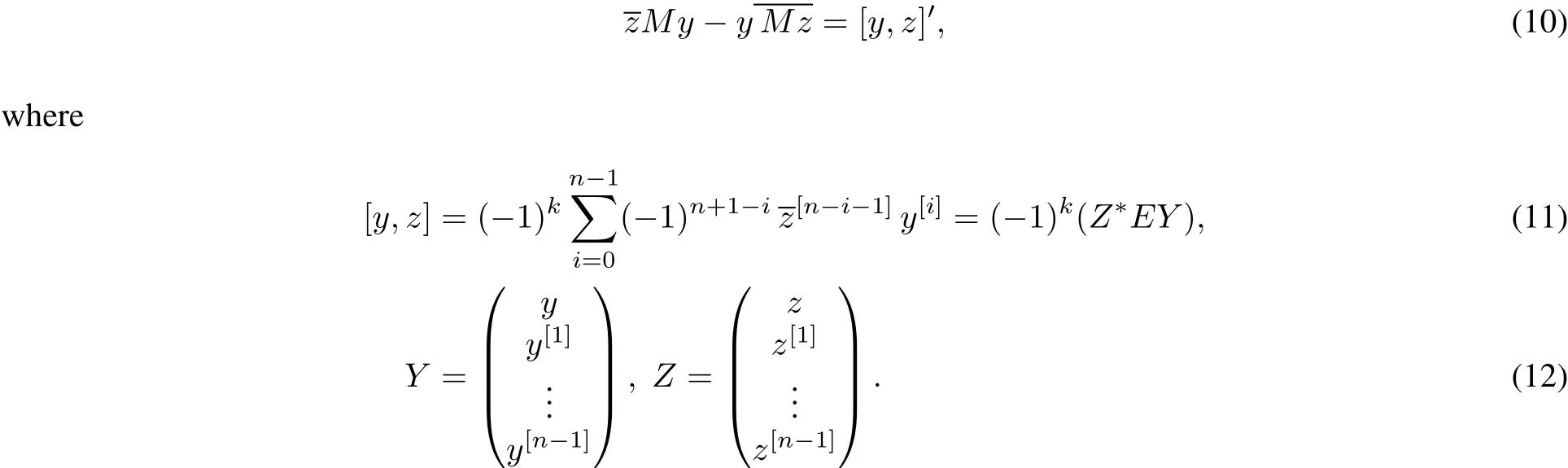
Definition 2.3[Regular Endpoints]Let Q∈Zn(J,R),J=(a,b).The expression M=MQis said to be regularat a if for some c,a＜c＜b,we have

Similarly the endpoint b is regular if for some c,a＜c＜b,we have

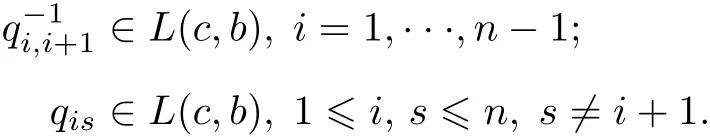
Note that,from(1)it follows thatif the above hold for some c∈J then they hold for any c∈J.We say that M is regularon J,orjust M is regular,if M is regularatboth endpoints.

3 Notation and basic assumptions for two-intervals

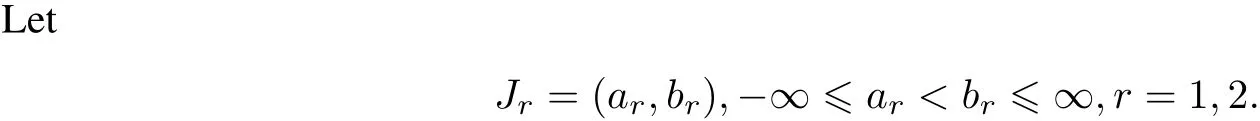
Define two differentialexpressions with real-valued coefficients by

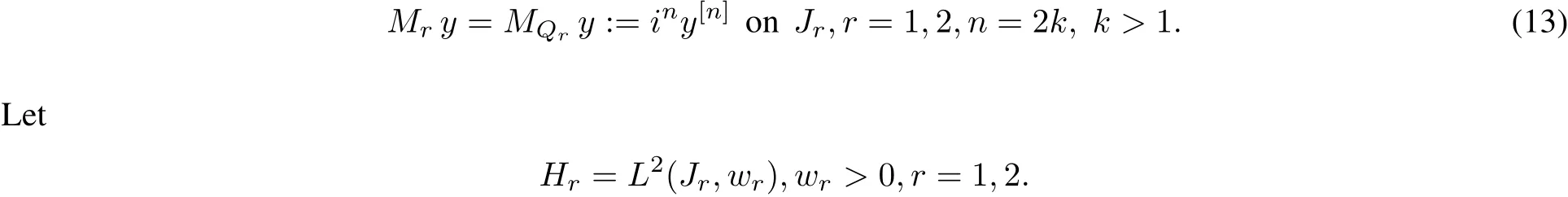
The two-intervalmaximaland minimaldomains and operators are simply the directsums of the corresponding oneintervaldomains and operators

Elements of Hu=H1+H2willbe denoted in bold face type:f={f1,f2}with f1∈H1,f2∈H2.As usualthe innerproductin Huis defined by

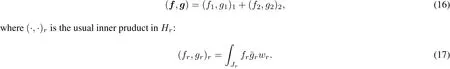
In this paper,following[10]we replace the directsum innerproduct(16)by

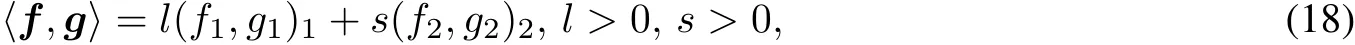
and apply operatortheory in the directsum space

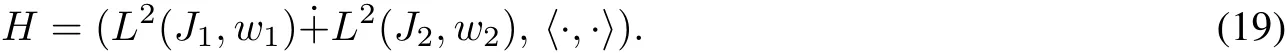
Remark 3.1 For any positive numbers l and s,(18)is an inner product in H.The underlying set of the Hilbertspace H defined by(19)is the same as thatof the usualdirectsum Hilbertspaces Hu,thus these spaces are differentiated from each other only by their inner products.As we willsee below the parameters l,s influence the boundary conditions which yield self-adjointrealizationsofthe equationsin the two-intervalcase.From another perspective,we observe also thatthe Hilbertspace(19)can be described as a′′usual′′directsum space Huwith summands H1=L2(J1,lw1),H2=L2(J2,sw2).

As in the one intervalcase the Lagrange sesquilinearform plays an importantrole.Itis defined,for appropriate functions f,g,by

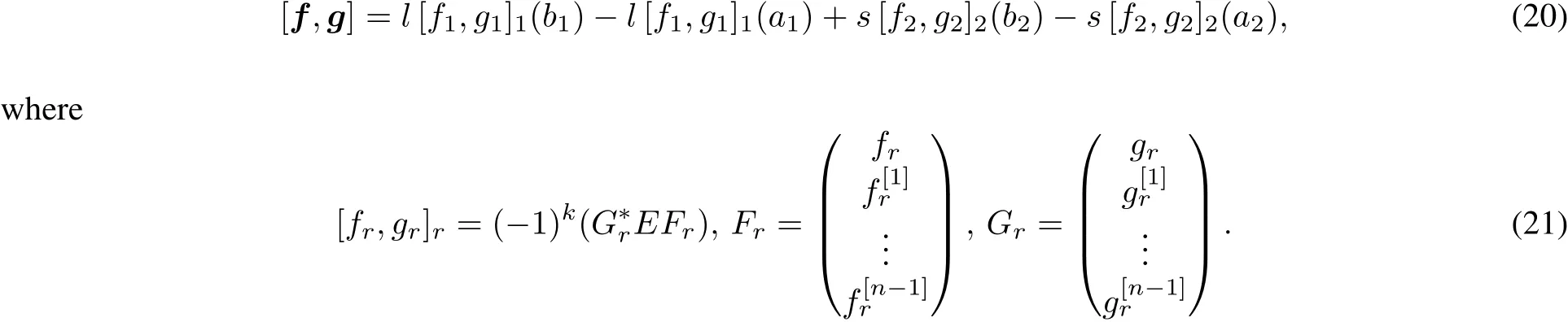
Note that the two-interval Lagrange form[f,g]connects all four endpoints with each other and depends on the parameters l,s.

4 Characterization ofallself-adjointdomains fortwo-intervalproblems

In this section we assume that MQr(r=1,2)are generated by Qr∈Zn(r)(Jr,R)satisfying(7),n=2k, k＞1.Firstwe give some preliminary lemmas.

Lemma 4.1 We have

In particular,

2.The minimal operator Sminis a closed,symmetric,densely defined operator in the Hilbert space H with deficiency index d given by d=d1+d2.

Proof The proofgiven in[3]for(16)extends readily to(18).

Definition 4.1 Assume that ar≤αr＜βr≤brand Srminare defined on(αr,βr)as above.Then the deficiency indexes drof Srminare the numberof linearly independentsolutions of

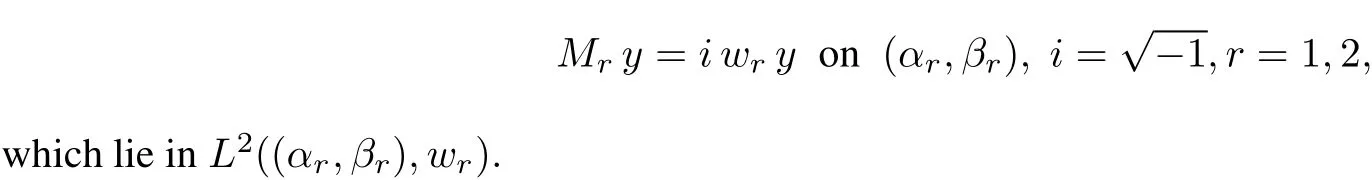
Lemma 4.2 Let ar≤αr＜βr≤br.The number drof linearly independentsolutions of

lying in L2((αr,βr),wr)is independentofλr∈C,provided Im(λr)/=0.If one endpointof(αr,βr)is regular and the otheris singularthen the inequalities

hold.Forλ=λr∈R,the numberof linearly independentsolutions of(22)r=1lying in L2((α1,β1),w1)is less than orequalto d1and the numberoflinearly independentsolutionsof(22)r=2lying in L2((α2,β2),w2)isless than or equalto d2.

Let cr∈(ar,br)=Jr,r=1,2.

a.If d11is the deficiency index on(a1,c1),d12is the deficiency index on(c1,b1)and d1is the deficiency index on(a1,b1),then

b.If d21is the deficiency index on(a2,c2),d22isthe deficiency index on(c2,b2)and d2isthe deficiency index on(a2,b2),then

Proof For the proofof the previous statementsee Lemma 4 in[8].The statementof a and b see Lemma 7 in [7].

Nextwe give the Everittand Zettl[5]extension ofthe GKN Theorem from the one intervalto the two-interval case.

Lemma 4.3 Let Sminbe the two intervalminimaloperator in H and let d be the deficiency index of Smin. A linear submanifold D(S)of Dmaxis the domain of a self-adjointextension S of Sminif and only if there exist vectors w1,w2,···,wdin Dmaxsatisfying the following conditions:

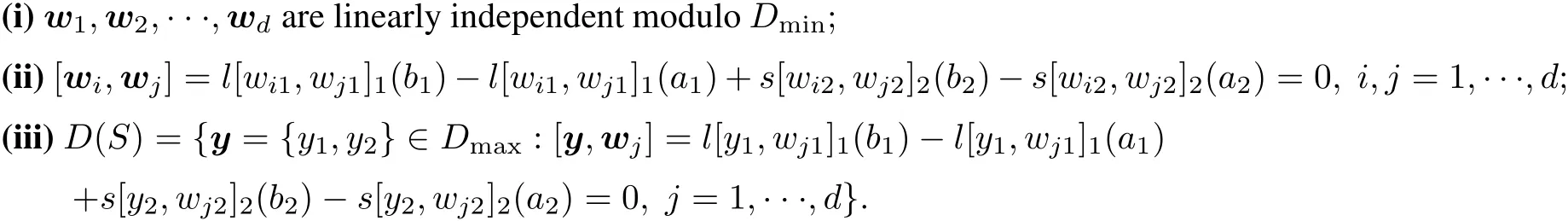
Proof See Theorem 3.1 and Corollary 3.3 in Everitt and Zettl[5]for the case with inner product(16),the adaptation to innerproduct(18)is routine.

Remark 4.1 As mentioned in the Introduction,the characterization of Lemma 4.3 depends on the maximal domain vectors wj,j=1,···,d.These vectors depend on the coefficients of each differential equation and this dependence is implicitand complicated.Nextwe give more explicitequivalentconditions for(i)-(iii)of Lemma 4.3.

The nexttheorem is our main resultin this paper.

Theorem 4.1 Let Mrbe a symmetric differentialexpression on(ar,br)and let cr∈(ar,br).Letthe Lagrange form[·,·]be given by(20),d1=d11+d12−n,d2=d21+d22−n,mr=2d1r−n and nr=2d2r−n.Then d1is the deficiency index of(22)r=1on(a1,b1)and d2is the deficiency index of(22)r=2on(a2,b2)and d=d1+d2. A linearsubmanifold D(S)of Dmaxis the domain ofa self-adjointextension S of Sminifand only ifthere exists a complex d×m1matrix A1and a complex d×m2matrix B1and a complex d×n1matrix A2and a complex d×n2matrix B2such thatthe following three conditions hold:

Here u1,...,um1,v1,...,vm2,g1,...,gn1and z1,...,zn2are solutions of LC type on(a1,c1),(c1,b1), (a2,c2)and(c2,b2),respectively,as constructed in[6]and Ejis the symplectic matrix(7)of order j.For details ofthe definition and construction of LC solutions see[6].

Proof The proof consists of applying Theorem 4.12 in[8]with the weight functions w1,w2replaced by w1/l,w2/s,respectively.Note that rank(A1,B1,A2,B2)=rank(lA1,lB1,sA2,sB2)for any l＞0,s＞0. Proceeding as in[8]we note that the introduction of the parameters l,s into the weight functions results in the Lagrange form(20)in place of[f,g]=[f1,g1]1(b1)−[f1,g1]1(a1)+[f2,g2]2(b2)−[f2,g2]2(a2).

The proofof Theorem 4.1 is completed by choosing

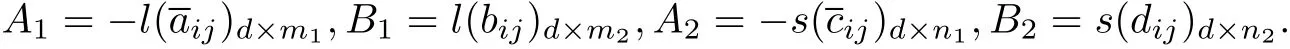
See also the proof of Theorem 9 of[7]or Theorem 4 of[6].They are the one-intervalcase and revealthe basic strategy.

In Theorem 4.1,itis assumed thatallfourendpoints a1,b1,a2,b2are singular.Itcan be specialized to known results when one ortwo orthree orfourendpointsare regular.Theorem 4.1 reducesto Theorem 2 in[12]when one endpointof each interval(a1,b1),(a2,b2)is regular.We have either a1is regular,b1is singular,a2is regular,b2is singular or a1is singular,b1is regular,a2is singular,b2is regular,or a1is singular,b1is regular,a2is regular,b2is singular,or a1is regular,b1is singular,a2is singular,b2is regular.We state one case here for the convenience of the reader.

Theorem 4.2 Let the hypotheses and notation of Theorem 4.1 hold and assume that a1and a2are regular. Then d=d12+d22.The solutions v1,v2,···,vd12and z1,z2,···,zd22can be extended to solutions on(a1,b1)and (a2,b2)such that v1,v2,···,vd12∈L2((a1,b1),w1)and z1,z2,···,zd22∈L2((a2,b2),w2).Let m2=2d12−n and n2=2d22−n.A linear submanifold D(S)of Dmaxis the domain of a self-adjointextension S of Sminif and only ifthere exists a complex d×n matrix A1and a complex d×m2matrix B1and a complex d×n matrix A2and a complex d×n2matrix B2such thatthe following three conditionshold:

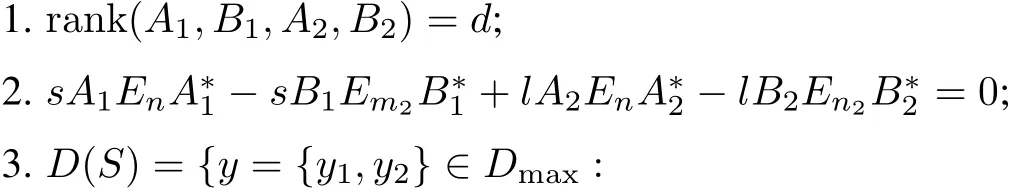
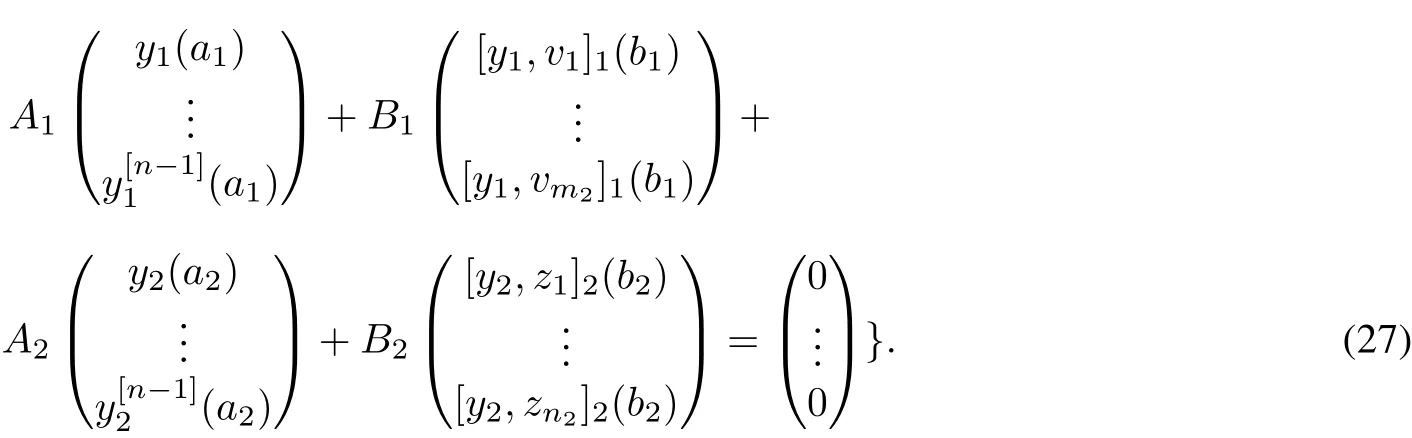
Proof The proofis a combination of Theorem 4.14 in[8]and Theorem 2 in[12].

5 Examples

To illustrate the self-adjointboundary conditions given by Theorem 4.1 we give a number of examples.Here we give examples for

Similar examples can be easily constructed for allhigher order cases n=2k,k＞2.Since the conditions when d=0 or 1 are the same as in the one intervalcase and are independentof l and s.In these cases the self-adjoint extensions in the Hilbert space H defined by(18)are the same as those of the usual direct sum Hilbert space Hudefined by(16).So we give examples here only for d=2,d=3,d=4,d=5,d=6,d=7 and d=8.

Example 5.1 Assume d11=2,d12=3,d21=3,d22=2.Then d1=d11+d12−4=1,d2=d21+d22−4= 1,d=d1+d2=2 and m1=2d11−4=0,m2=2d12−4=2,n1=2d21−4=2,n2=2d22−4=0. Suppose thatthe boundary conditionsat b1,a2are coupled:

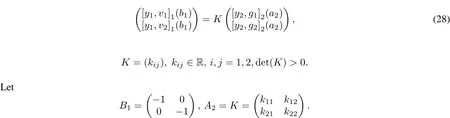
Then rank(B1,A2)=2.From a straightforward computation,itfollows that

sB1E2=lA2E2is equivalentwith s=l det(K).

By Theorem 4.1 we have if l=1,and det(K)=s＞0,then the boundary conditions(28)are self-adjoint.

Remark 5.1 Note that s＞0 is needed to preserve the positivity of the inner product(18).Using appropriate multiples ofthe usualinnerproduct,orchanging the weightfunction w2to sw2we can generate self-adjointoperators for any realcoupling matrix K satisfying det(K)=s＞0.This contrasts with the results in[8],using the weight function w2which requires that det(K)=1 for self-adjointness.We see that the parameter s plays a role in establishing the self-adjointboundary conditions.

Example 5.2 Assume d11=2,d12=3,d21=3,d22=3.Then d1=1,d2=2,d=3 and m1=0,m2= 2,n1=2,n2=2.Consider separated condition at a2and coupled conditions at b1,b2:

In this case rank(B1,A2,B2)=3 and A2E2=0.Then in terms of Theorem,we obtain the equivalence ofthe conditions for self-adjointness:

So,if l=1,and det(K)=−s＜0 then boundary conditions(29)are self-adjoint.

Note thatby studying the two-intervaltheory in directsum spaces with innerproductmultiples we obtain selfadjointoperators forany realcoupling matrix K satisfying det(K)=−s＜0.This contrasts with the results in[8] which require det(K)=−1.

Example 5.3 Assume d11=3,d12=3,d21=3,d22=3.Then d1=2,d2=2,d=4 and m1=2,m2= 2,n1=2,n2=2.Consider two pairs of coupled conditions:

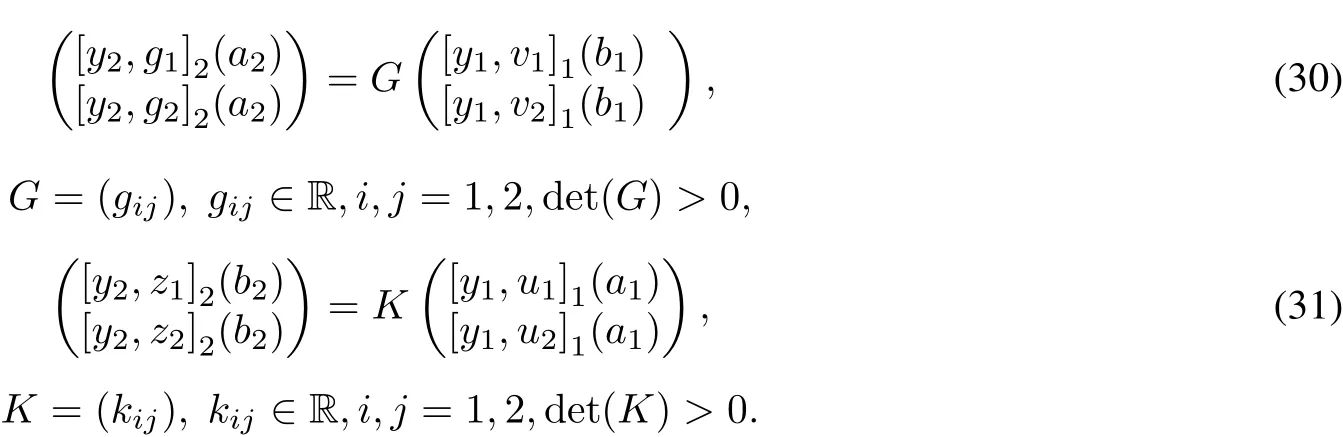
Proceeding as in the previousexample we obtain the equivalence ofconditions forself-adjointness:

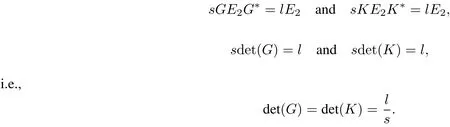
This shows that(30)and(31)are self-adjointboundary conditionswhen positive numbers l,s satisfy det(G)= det(K)=l/s.

Example 5.4 Assume d11=2,d12=4,d21=4,d22=3.Then d1=2,d2=3,d=5 and m1=0,m2= 4,n1=4,n2=2.Considerseparated conditionsat b2and coupled conditionsat b1,a2:

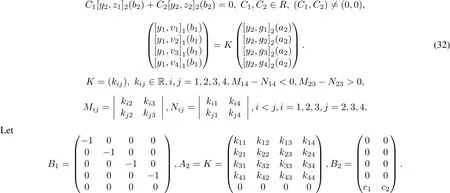
In this case rank(B1,A2,B2)=5 and B2E2=0.Then in terms of Theorem 4.1,we obtain the equivalence of the conditions forself-adjointness:

If we choose l=1,and s＞0 satisfies M14−N14=−s,M23−N23=s and(1),(2),(3),(4),then boundary conditions(32)are self-adjoint.

Remark 5.2 Using appropriate multiples of the usualinnerproduct,we establish self-adjointoperators for any realcoupling matrix K satisfying M14−N14=−s＜0,M23−N23=s＞0 and(1),(2),(3),(4).This contrasts with the results in[8]which requires M14−N14=−1,M23−N23=1 and(1),(2),(3),(4).

Example 5.5 Assume d11=4,d12=3,d21=3,d22=4.Then d1=3,d2=3,d=6 and m1=4,m2= 2,n1=2,n2=4.Consider two pairs of coupled conditions:

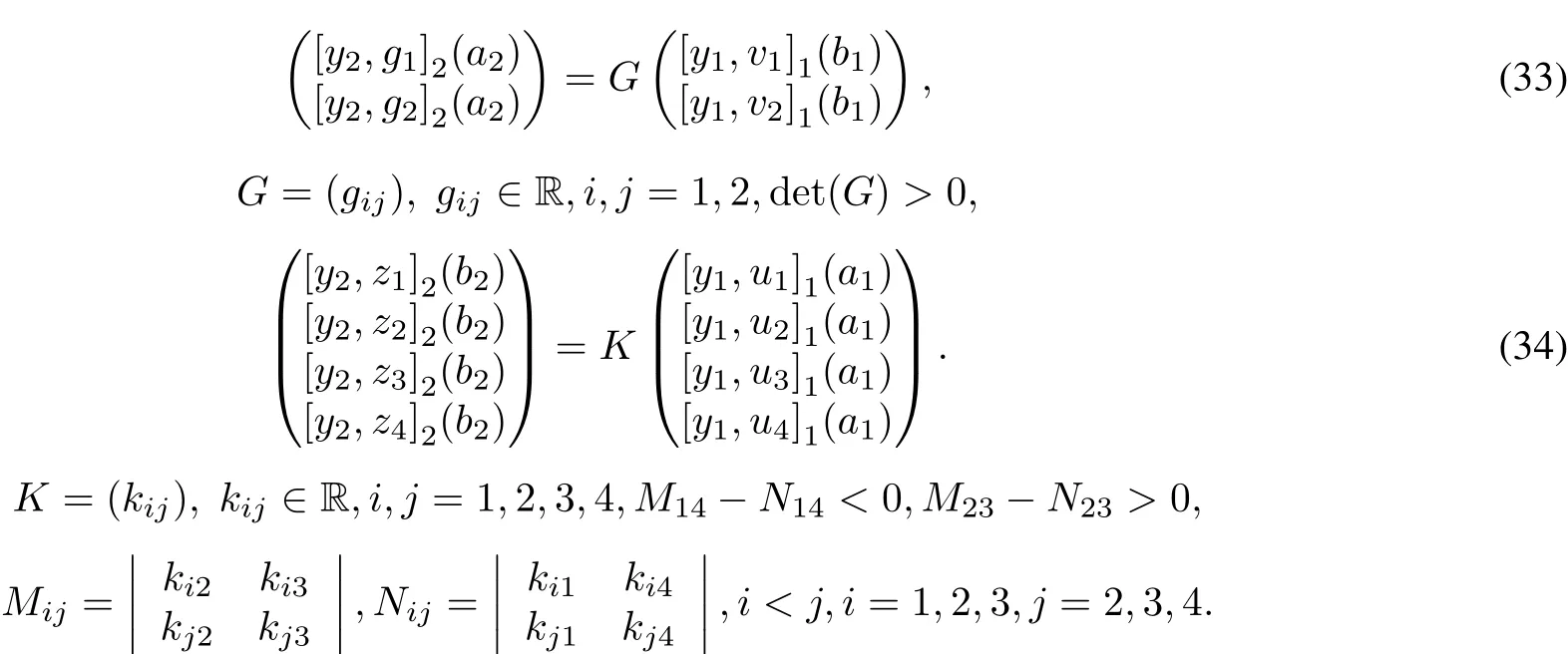
Proceeding as in the previous example we obtain the equivalence of conditions for self-adjointness:

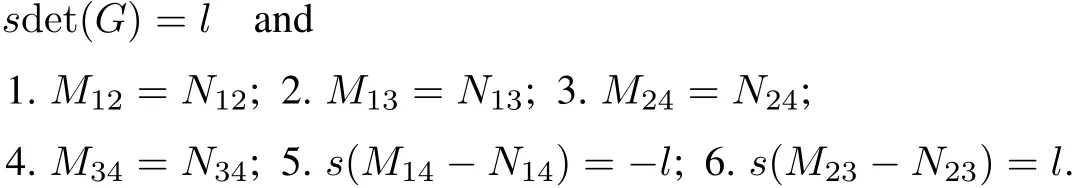
Ifwe choose s=1,and l＞0 satisfies det(G)=l＞0 and M14−N14=−l＜0,M23−N23=l＞0 and (1),(2),(3),(4),then the boundary conditions(33)and(34)are self-adjoint.

Remark 5.3 Using appropriate multiples of the usualinnerproduct,we establish self-adjointoperators for any realcoupling matrix K satisfying det(G)=l＞0 and M14−N14=−l＜0,M23−N23=l＞0 and(1),(2),(3), (4).This contrasts with the results in[8]which requires det(G)=1 and M14−N14=−1,M23−N23=1 and (1),(2),(3),(4).

Example 5.6 Assume d11=3,d12=4,d21=4,d22=4.Then d1=3,d2=4,d=7 and m1= 2,m2=4,n1=4,n2=4.Considerseparated conditions at a1and at b1and coupled conditions at a2,b2:

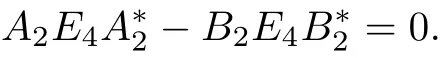
Then sA1E2−sB1E4B=0 for any s since A1E2=0=B1E4.In terms of Theorem,the boundary conditions(35)and(36)are self-adjointifand only if rank(A2,B2)=4 andNote thatthese conditions are independentof l and s and are simply the one-intervalself-adjointness conditions for each of the two intervals separately.Thus the above example justgives the two-intervalself-adjointness conditions which are generated by the directsum ofself-adjointoperators from each ofthe two intervals separately.

The nextexample involvesinteractionsbetween endpointsofthe two intervals and thus generatesa self-adjoint operatorwhich is nota directsum ofoperatorsfrom each ofthe two intervals.

Example 5.7 In the maximal deficiency case d=8,we have d11=4,d12=4,d21=4,d22=4, d1=4,d2=4,and m1=4,m2=4,n1=4,n2=4.Considertwo pairs ofcoupled conditions: Proceeding as in the previousexample we obtain the equivalence ofconditions forself-adjointness:

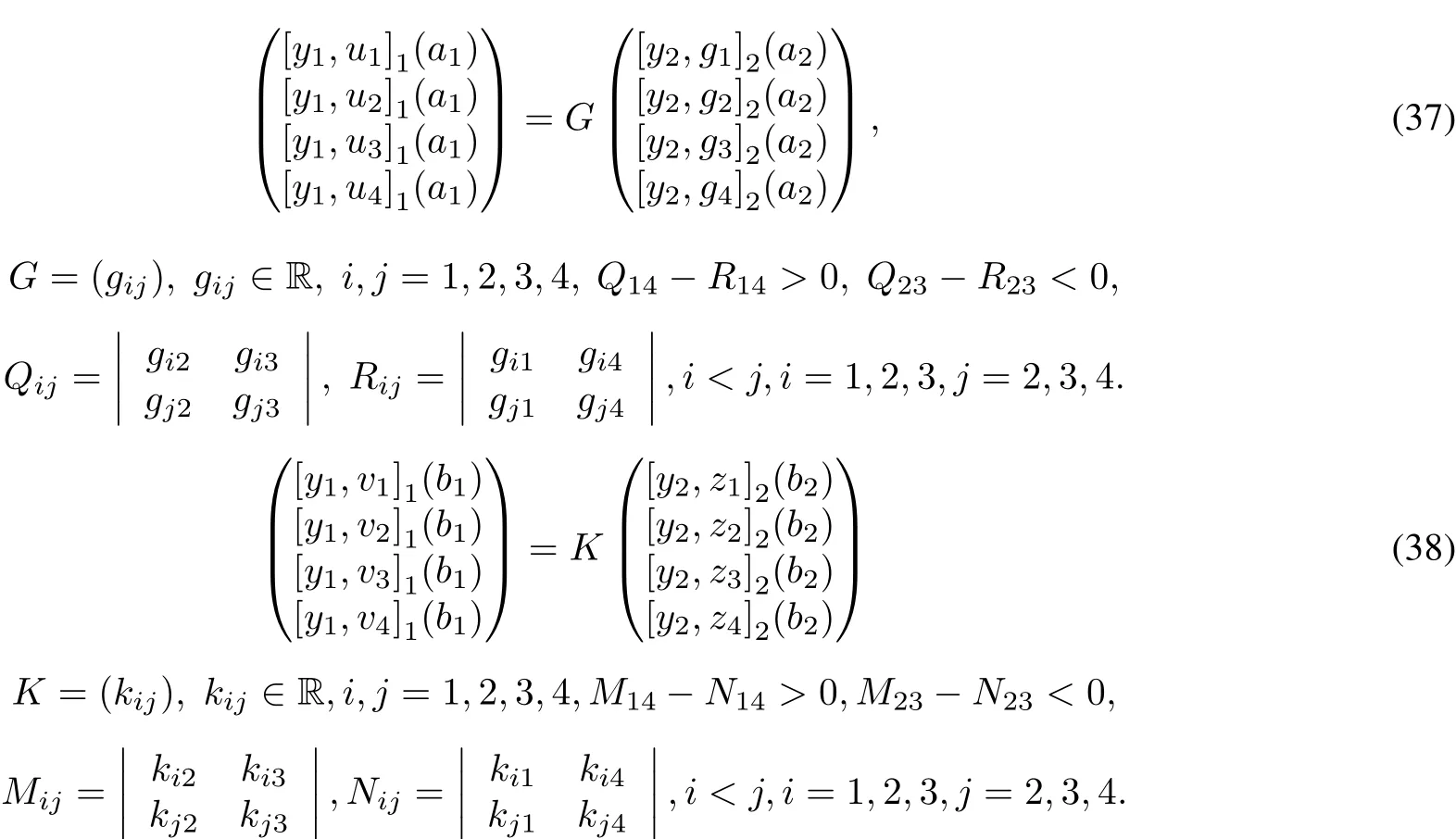
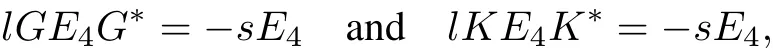
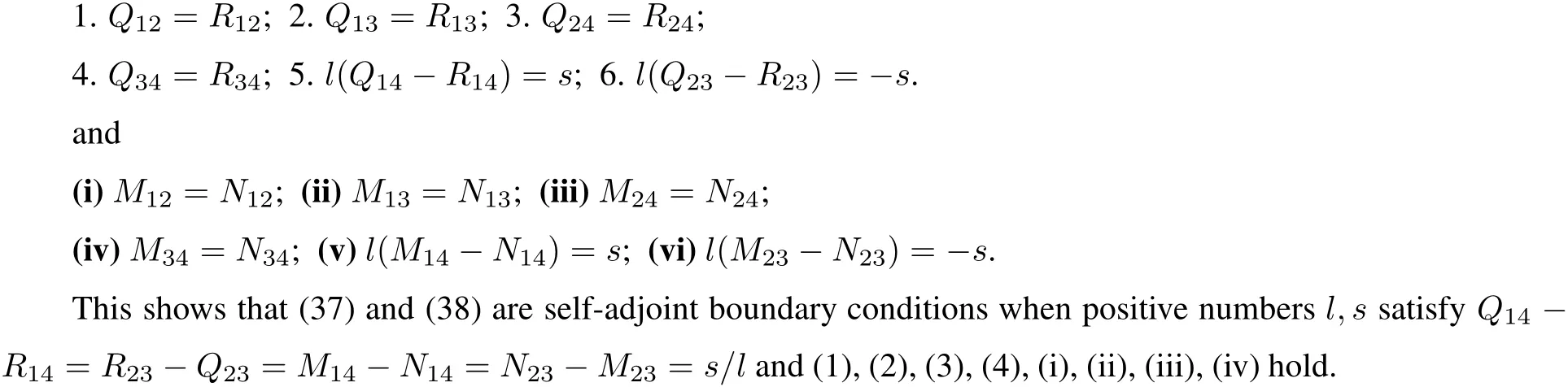
[1]Boyd JP.Sturm-liouville eigenvalue problems with an interiorpole[J].JMath Physics,1981,22(8):1575-1590.

[2]Gesztesy F,Kirsch W.One-Dimensional schr¨odinger operators with interactions singular on a discrete set[J].J Reine u Ang Mathematic,1985,362:28-50.

[3]EverittWN,ZettlA.Sturm-liouville differentialoperators in directsum spaces[J].Rocky Mountain JMath,1986,16(16): 497-516.

[4]Zettl A.Sturm-liouville theory[M].RI:American Mathematical Society,2005.

[5]Everitt WN,Zettl A.Differentialoperators generated by a countable number of quasi-differentialexpressions on the line [J].Proc London Math Soc,1992,64(3):524-544.

[6]Wang A P,Sun J,Zettl A.Characterization of domains ofself-adjointordinary differentialoperators[J].Journalof DifferentialEquations,2009,246:1600-1622.

[7]Hao X L,Sun J,Wang A P,etal.Characterization of domains of self-adjointordinary differentialoperatorsЦ[J].Results in Mathematics,2012,61:255-281.

[8]Suo J Q,Wang WY.Two-intervaleven order differentialoperators in directsum spaces[J].Results in Mathematics,2012, 62:13-32.

[9]Mukhtarov O S,Yakubov S.Problems for differential equations with transmission conditions[J].Applicable Analysis, 2002,81:1033-1064.

[10]Wang A P,Sun J,Zettl A.Two-intervalsturm-liouville operators in modified hilbertspaces[J].J Math Anal Appl,2007, 328:390-399.

[11]Sun J,Wang A P,Zettl A.Two-interval sturm-liouville operators in direct sum spaces with inner product multiples[J]. Results in Mathematics,2007,50:155-168.

[12]Suo J Q,Wang W Y.Two-intervaleven order Differential Operators in modified Hilbert Spaces[J].Bulletin of the Australian Mathematical Society,2012,85:241-260.

O 175.3 Document code:A Article ID:1000-5137(2017)03-0393-13

10.3969/J.ISSN.100-5137.2017.03.007

date:2016-11-21

This work is supported by Natura Science Foundation of China(11361039);Specialized Research Fund for the Doctoral Program of Higher Education(20131501120006).

∗Corresponding author:Suo Jianqing,lecturer,research area:spectraltheory of differentialoperators,E-mail:sjq.hello@ 163.com