Rational quadratic trigonometric Bézier curve based on new basis with exponential functions

Wu Beibei,Yin Junfeng,LiChunjing,Jin Meng(.Schoolof Mathematical Science,Tongji University,Shanghai200092,China; 2.Schoolof Mathematics and Physics,Shanghai University of Electric Power,Shanghai200090,China)

Rational quadratic trigonometric Bézier curve based on new basis with exponential functions

Wu Beibei1,2∗,Yin Junfeng1,LiChunjing1,Jin Meng1
(1.Schoolof Mathematical Science,Tongji University,Shanghai200092,China; 2.Schoolof Mathematics and Physics,Shanghai University of Electric Power,Shanghai200090,China)

We constructa rationalquadratic trigonometric B´eziercurve with fourshape parameters by introducing two exponentialfunctions into the trigonometric basis functions in this paper.It has the similar properties as the rationalquadratic B´ezier curve.Forgiven controlpoints,the shape ofthe curve can be flexibly adjusted by changing the shape parameters and the weight.Some conics can be exactly represented when the controlpoints,the shape parametersand the weightare chosen appropriately.The C0,C1and C2continuousconditionsforjoining two constructed curves are discussed.Some examples are given.

quadratic trigonometric basis functions;rationalquadratic trigonometric B´ezier curve; shape parameters;exponentialfunctions

∗Corresponding author:Wu Beibei,associate professor,reseach area:computer aided geometric design,E-mail:beibei wu@126.com

1 Introduction

In geometric modeling and computergraphics,forefficiently improving the shape of the curves,some methods of generating curves were presented by incorporating shape parameters,trigonometric or exponentialfunctions into the classical basis functions(cf.[1-8]).In the past ten years,B´ezier form of trigonometric curves with shape parameters has received very much attention in CAGD through to the efforts of many researchers.For example, Han proposed quadratic trigonometric B´ezier curves and cubic trigonometric B´ezier curves with a shape parameter in[9]and[10]respectively.Han etalintroduced the cubic trigonometric B´ezier curve with two shape parameters in [11].Sheng etalconstructed the quasi-quartic B´ezier-type curves with a shape parameterin[12].Bashiretalgave a class of quasi-quintic trigonometric B´ezier curve with two shape parameters in[13].Hussain etalpresented the C1rationalquadratic trigonometric polynomialspline with two shape parameters in[14].

We define a new rationalquadratic trigonometric B´ezier curve with four shape parameters by introducing two exponentialfunctions into the basis functions in this paper.Itis more flexible to controlthe shape than the presented curve in[15].The constructed curve inherits mostgeometric properties of the rationalquadratic B´ezier curve.Itcan be used to exactly representsome conics like ellipses,circles and parabolas.The condition of C2continuity between two constructed curves is discussed.Some examples illustrate that the constructed curve in this paper provides an effective method for designing curves and geometric modeling.

The structure of this paper is as follows.Section 2 defines the quadratic trigonometric B´ezier basis functions with fourshape parameters.Section 3 constructs the rationalquadratic trigonometric B´ezier curve with fourshape parameters.Section 4 gives the effectof the shape of the curve by the shape parameters and the weight.Section 5 discusses the composite constructed curves.Section 6 is the conclusion.

2 Quadratic trigonometric B´ezier basis functions with fourshape parameters

By introducing two exponentialfunctions into the basis functions,we define a kind ofquadratic trigonometric basis functions with fourshape parameters and discuss some properties.

Definition 1 Letα,β∈[−1,1],λ,µ∈[0,+∞),for t∈[0,1],the following three functions are defined to be the new quadratic trigonometric B´ezier basis functions with four shape parametersα,β,λandµ:

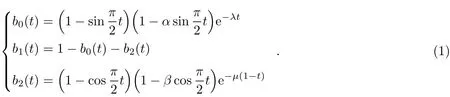
Theorem 1 The basis functions(1)have the following properties:

(i)Nonnegative property:bi(t)≥0 for i=0,1,2.

(iii)Symmetry:bi(t;α,β,λ,µ)=b2−i(1−t;β,α,µ,λ)for i=0,1,2.

(iv)Propertiesatthe endpoints:

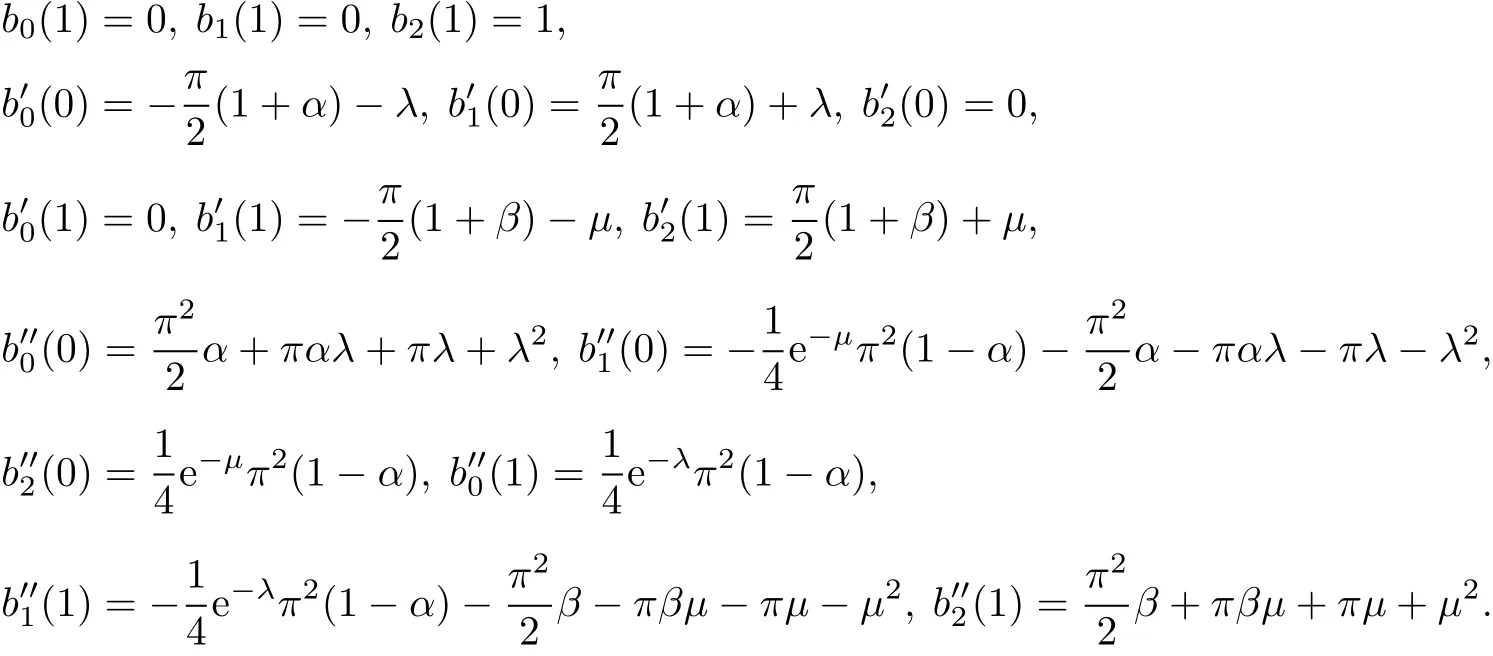
(v)Monotonicity:For fixed t∈[0,1],b0(t)is monotonically decreasing for shape parametersαandλ;b2(t) is monotonically decreasing for shape parametersβandµ;b1(t)is monotonically increasing respectively for shape parametersα,β,λandµ.

Proof The results can be obtained immediately from the definition of the basis functions in(1).

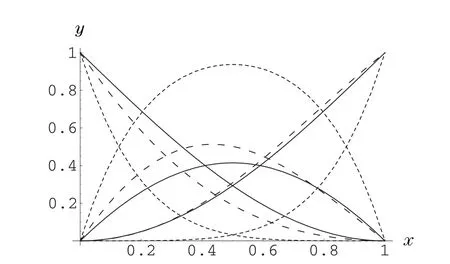
Figure 1 The new quadratic trigonometric B´ezier basis functions

Figure 1 shows the curves ofthe quadratic trigonometric Be´zierbasis functions forα=β=λ=µ=0(solid lines),forα=β=1,λ=µ=2(shortdashed lines),and forα=,=−,λ=0,µ=(long dashed lines).

3 Rationalquadratic trigonometric B´ezier curve with four shape parameters

We define a rationalquadratic trigonometric B´eziercurve with fourshape parametersα,β,λandµas follows.

Definition 2 Suppose thatwe are given three controlpoints Qi(i=0,1,2)in R2.The following function

is called the rationalquadratic trigonometric B´eziercurve(RQTBC,forshort)with fourshape parameters,where the weightω＞0,and the basis functions bi(t)(i=0,1,2)are defined in(1).

Some properties of the RQTBC can be obtained easily from the properties of the basis functions(1).

Theorem 2 The RQTBC(2)holds the following properties:

(i)Terminalproperties:

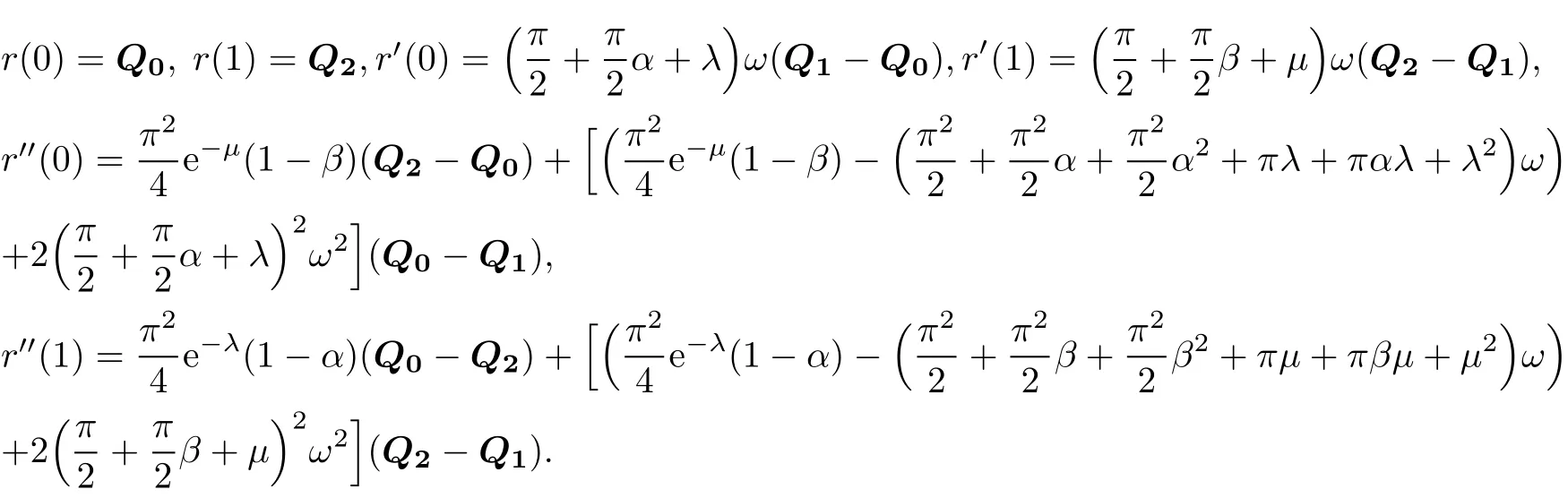
(ii)Symmetry:ifthe weightωiskeptfixed,Q0,Q1,Q2and Q2,Q1,Q0define the same RQTBC in different parameterizations,i.e.,

(iii)Geometric invariance:The shape of a RQTBC is independentofthe choice of coordinates,i.e.,itsatisfies the following two equations:

where q is an arbitrary vector in R2,and T is an arbitrary 2×2 matrix.

(iv)Convex hull property:The entire RQTBC segment must lie inside its control polygon spanned by Q0,Q1,Q2.

Note Ifω=1,the RQTBC willreduce to the quadratic trigonometric Be´ziercurve with fourshape parameters. Ifλ=µ=0,the RQTBC willreduce to the rationalquadratic trigonometric Be´ziercurve with two shape parameters in[15].Ifα=β=−1,λ=µ=0,the RQTBC willreduce to R(t)=co+sin∈[0,1], which is a straightline between the controlpoints Q0and Q2.

4 Shape controlof the RQTBC

The presence of shape parameters and the weightprovide an intuitive controlon the shape of the curve.

Figure 2 illustrates the effects of the shape parameters and the weighton the RQTBC.Figure 2(a)shows the curves with four fixedβ=λ=0,µ=ω=2,α=−(long dashed lines),0(solid lines)and 1(shortdashedlines).Figure 2(b)shows the curves with four fixedα=µ=0,λ=,ω=2,β=−(long dashed lines),0 (solid lines)and 1(shortdashed lines).Figure 2(c)shows the curves with fourfixedα=−1,β=1,µ=0,ω=2, λ=0(solid lines),2(long dashed lines)and 4(shortdashed lines).Figure 2(d)shows the curves with fourfixed α=,β=−,λ=0,ω=2,µ=0(solid lines),1(long dashed lines)and 5(shortdashed lines).Figure 2(e)shows the curves with four fixedα=0,β=1,µ=λ=,=1(long dashed lines),2(solid lines)and 4(short dashed lines).

For the same shape parametersα=m andβ=n,it is shown from Figure 2(c)and(d)that the RQTBC is closer to the controlpolygon than the curve in[15]by altering the values ofλandµof the exponentialfunctions.Ifλ→+∞,the RQTBC willreduce to a straightline between the controlpoints Q1and Q2.Ifµ→+∞,the RQTBC willreduce to a straightline between the controlpoints Q0and Q1.

Given the proper controlpoints,the shape parameters and the weight,the corresponding RQTBC can be used to representsome specialcurves exactly,such as ellipses,circles,parabolas,and line segments.Figure 3 shows the arc of an ellipse,the arc of a circle and the arc of a parabola.

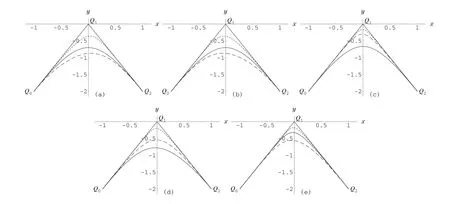
Figure 2 Effecton the shape ofthe curve with differentparameters and weight

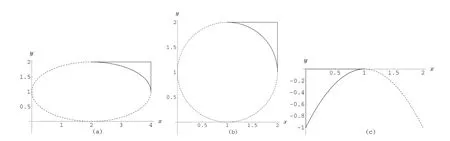
Figure 3 The representation ofconics with RQTBC.(a)ellipse;(b)circle;(c)parabola

5 Continuity ofthe curves

Leta RQTBC r(t)be given as(2)and a second RQTBC r∗(t)be defined by

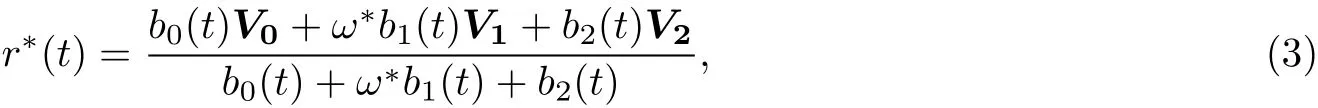
where the weightω∗＞0,fourshape parameters,∈[−1,1],λ∗,µ∗∈[0,+∞).

Theorem 3 Given two segments of r(t)and(t),then the necessary and sufficientcondition of continuity is

(iii)for C2continuity,V2=Q0+ν(Q2−Q1),

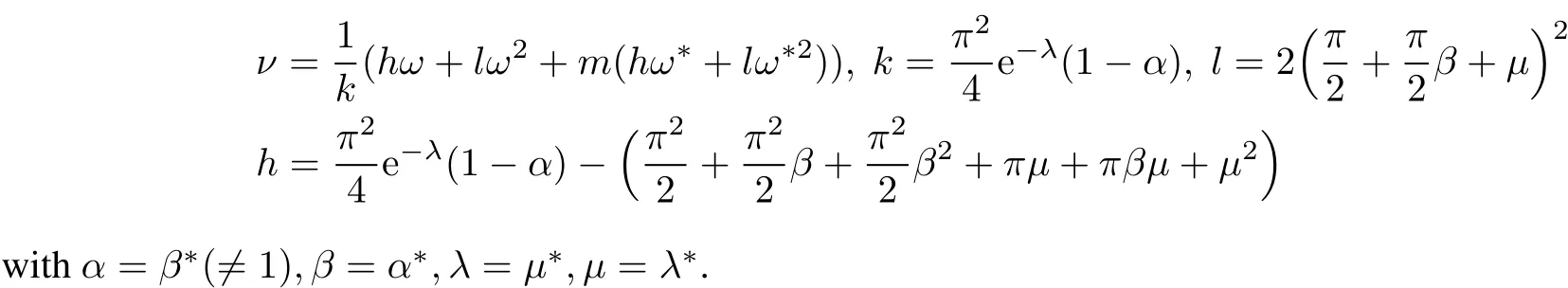
Proof The result(i)is obvious for r∗(0)=r(1).

For C1continuity,the tangents of the two curves atthe jointmustbe equal,thatis,

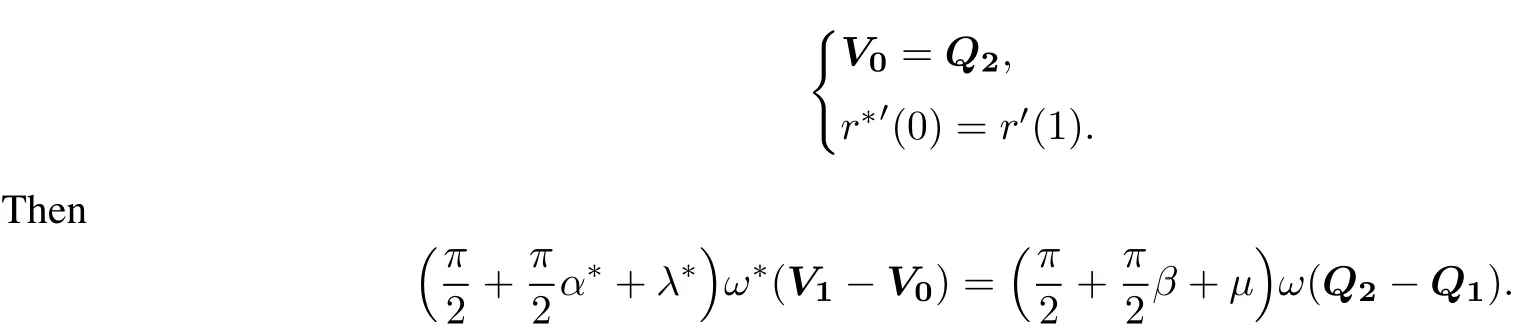
The result(ii)holds aftersimple reorganization.

The two curves are joined by C2continuity if

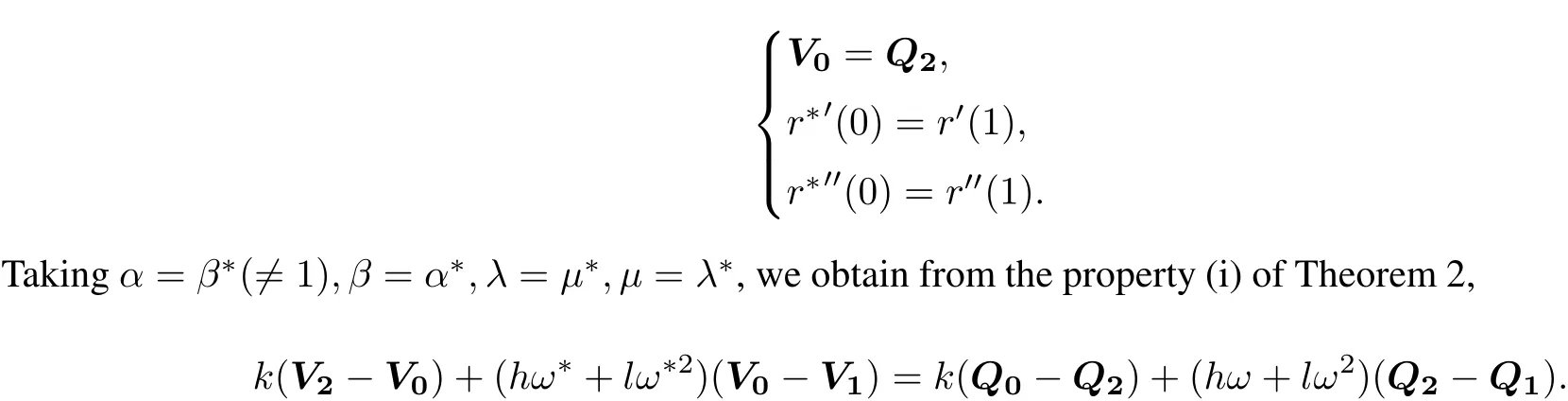
Since V1−V0=m(Q2−Q1)and V0=Q2,the result(iii)follows.

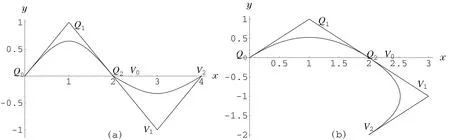
Figure 4 The continuity of the two curves(a)C1continuity(b)C2continuity

6 Conclusion

The presented RQTBC has mostof the similar geometric properties of the traditionalrationalquadratic B´ezier curve and can accurately represent some conics.The composition of two curve segments using C0,C1and C2continuity conditions is discussed.The shape of the curve can be adjusted by altering the values of shape parameters and the weightwhile the controlpolygon is keptunchanged.The new curves can be freely adopted in CAD/CAM systems.

[1]Zhang JW.C-curves:An Extension of Cubic Curves[J].Comput Aided Geom D,1996,13(3):199-217.

[2]Chen Q Y,Wang Z.A Class of B´ezier-like Curves[J].ComputAided Geom D,2003,20(1):29-39.

[3]Yan L L,Liang JF.An Extension ofthe B´ezier Model[J].ApplMath Comput,2011,218(6):2863-2879.

[4]Han X L.Quadratic Trigonometric Polynomial Curves Concerning Local Control[J].Appl Numer Math,2006,56(1):105-115.

[5]Han X L,Zhu Y P.Curve Construction Based on Five Trigonometric Blending Functions[J].BIT Numer Math,2012, 52(4):953-979.

[6]Han X L.Normalized B-basis ofthe Space of Trigonometric Polynomials and Curve Design[J].ApplMath Comput,2015, 251(C):336-348.

[7]Hoffmann M,Juh´asz I,K´arolyiG.A ControlPointBased Curve with Two Exponential Shape Parameters[J].BIT Numer Math,2014,54(3):691-710.

[8]Zhu Y,Han X L.Curves and Surfaces Construction Based on New Basis with ExponentialFunctions[J].Acta ApplMath, 2014,129(1):183-203.

[9]Han X L.Quadratic Trigonometric Polynomial Curves with a Shape Parameter[J].Comput Aided Geom D,2002, 19(7):503-512.

[10]Han X L.Cubic Trigonometric PolynomialCurves with a Shape Parameter[J].ComputAided Geom D,2004,21(6):535-548.

[11]Han X A,Ma Y,Huang X.The Cubic Trigonometric B´ezier Curve with Two Shape Parameters[J].ApplMath Lett,2009, 22(2):226-231.

[12]Sheng M,Su B.A Class of B´ezier-type Curves and Surfaces by Trigonometric Polynomials[J].J Comput Inform Syst, 2013,9(1):89-96.

[13]Bashir U,Abbas M,Awang M,etal.A Class of Quasi-quintic Trigonometric B´ezier Curve with Two Shape Parameters [J].ScienceAsia,2013,39S(1):11-15.

[14]Hussain M,Saleem S.C1Rational Quadratic Trigonometric Spline[J].Egypt Inform J,2013,14(3):211-220.

[15]Bashir U,Abbas M,Ali J.The G2and C2Rational Quadratic Trigonometric B´ezier Curve with Two Shape Parameters with Applications[J].Appl Math Comput,2013,219(20):10183-10197.

TP 391 Documentcode:A Article ID:1000-5137(2017)03-0410-07

date:2017-03-17

This research was supported by Natural Science Foundation of China(11271289,11502141);the Fundamental Research Funds for the Central Universities;the Key Program of NSFC-Guangdong Joint Fund of China(U1135003).

10.3969/J.ISSN.100-5137.2017.03.009

2010 MSC:65D18,68U05