潜堤上波浪传播过程数值研究

廖 斌，陈善群，任超洋

(安徽工程大学 建筑工程学院，安徽 芜湖 241000)

潜堤上波浪传播过程数值研究

廖 斌，陈善群，任超洋

(安徽工程大学 建筑工程学院，安徽 芜湖 241000)

以RANS方程结合Level-Set方法为研究基础，采用五阶WENO有限差分格式进行空间离散、三阶TVD Runge-Kutta格式进行时间推进、Level-Set方法追踪波浪与空气间自由面以及解析松弛法来实现数值水槽中的造波消波，建立了一种求解潜堤上波浪传播问题的数值计算模型。选取经典的潜堤上波浪传播物理试验模型对数值模型进行了验证，水位计算结果与试验值吻合较好。进一步研究了波高、潜堤顶部淹没深度以及潜堤坡度等参数对潜堤上波浪传播过程的影响。结果表明：波高越高、淹没深度越浅、潜堤向波坡度越小，波浪受浅水作用越明显；潜堤背波坡度越小，波浪受反浅水作用稍大，但并不明显。

潜堤；Level-Set方法；波浪传播；数值研究；浅水作用

1 研究背景

潜堤作为一种常见的护岸构筑物在防止波浪对海岸(尤其是开敞式海岸)的侵蚀过程中发挥着重要作用。研究潜堤上波浪传播过程，特别是波浪与空气间自由面的演化过程对波浪传播物理机制的深入理解以及临岸构筑物设计等方面具有非常重要的理论和工程实际意义。

相对于试验研究手段，数值模拟具有快捷、经济、不受计算范围及尺度约束、重复性好、在保证精度的条件下容易得到一般规律性结论的特点，使得数值模拟在波浪传播研究领域越来越受研究者的青睐。以往研究采用的数值模拟方法主要包括Boussinesq方程数值模型[1-3]、浅水方程数值模型[4-5]以及雷诺时均Navier-Stokes(简称RANS)方程结合界面追踪数值模型[6-8]3种。其中，Boussinesq方程数值模型和浅水方程数值模型均没有考虑波浪和空气之间的相互作用，只适用于求解浅水效应引起的波浪变形问题，不适用于碎波条件下波浪水位问题的求解。刘忠波等[9]将破碎项引入Boussinesq方程仍不能很好地解决碎波条件下波浪水位问题；采用RANS方程结合界面追踪数值模型考虑了自由面演化过程中波浪和空气之间的相互作用以及流体黏度和湍流流动的影响，具有解决碎波条件下波浪水位问题的能力，是一种较为直接的求解模型，但目前使用这种求解模型的方法大多基于商业软件。商业软件中关于空间及时间离散精度以及边界条件设定的限制使得潜堤上波浪传播过程的数值模拟精度受到一定影响。为了克服商业软件的缺陷，本文拟建立一种求解潜堤上波浪传播问题的二维数值计算模型，并进行验证计算。用该模型进一步研究波高、潜堤顶部淹没深度以及潜堤坡度等参数对潜堤上波浪传播过程的影响。

2 数值模型的建立

2.1 Level-Set界面追踪方法

Level-Set方法由Osher等[10]于1988年提出，其中心思想是将随时间运动的2种物质间界面Γ(t)看作某个函数φ(x,t)的零等值面(线)，即构造函数φ(x,t)使得在任意时刻t，运动界面Γ(t)恰好是φ(x,t)的零等值面(线)，满足关系式

(1)

式中：Ω表示整个计算域；φ(x,t)又被称为Level-Set函数。

φ(x,t)的初值需满足在Γ(t)附近法向单调，在Γ(t)上始终为0。一般可取φ(x,t)为点x到t=0时刻界面Γ(0)的符号距离，关系式为

(2)

式中：d(x,Γ(0))表示点x到界面Γ(0)的最小距离；Ω1和Ω2分别表示第1种物质和第2种物质所处的计算域。

在任意时刻t，对于运动界面Γ(t)上的任意点x，都要保证φ(x,t)=0，从而函数φ(x,t)需满足关系式

(3)

式(3)被称为Level-Set方程，求解该方程即能得到任意时刻φ(x,t)的函数值，从而确定运动界面Γ(t)的位置。

由于在数值计算过程中容易产生误差，根据式(3)计算得到的φ(x,t)可能不再是t时刻点x到界面的距离，这将失去φ(x,t)的零等值面就是运动界面的意义。因此，为了保持φ(x,t)的符号距离性质，需对φ(x,t)作重新初始化，使其重新成为点x到界面Γ(t)的符号距离。重新初始化过程通过求解式(4)的初值问题来实现。

(4)

2.2 控制方程

本文选取不可压缩RANS方程，结合Level-Set方程求解潜堤上波浪传播问题，二维控制方程表达式为

(5)

式中：ui,uj均为时均速度；ρ为波浪密度；p为压强；ν为运动黏度；νT为涡黏系数；g为重力加速度。压强p和时均速度ui的耦合迭代求解采用预处理BiCGStab算法[11]，湍流模型选用k-ω模型[12]。

2.3 空间离散和时间推进格式

本文选取的空间离散格式为Jiang等[13]提出的五阶WENO有限差分格式，简称WENO5格式。WENO5格式将用于对流项中时均速度ui,k-ω湍流模型中的湍动能k和湍流耗散率ω,以及Level-Set函数φ的离散迭代求解。下面用Level-Set重新初始化过程为例说明WENO5格式的离散求解过程。

将式(4)进行有限差分，二维差分格式为

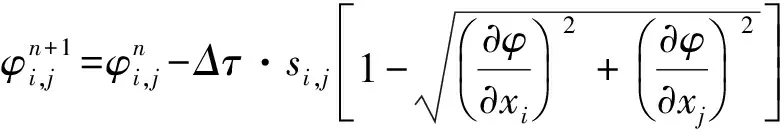
(6)

其中：

(7)

(8)

(9)

式中si,j为符号函数sign(φ)的简写。

式(7)中WENO5的定义式为

(10)

其中：

(11)

式中：IS1,IS2,IS3被称为光滑因子；ε表示一不为0的小量。时间推进格式为Shu等[14]提出的三阶TVDRunge-Kutta格式，表达式为

(12)

其中：

2.4 解析松弛法

解析松弛法最早由Mayer等[15]提出，并在消波中使用，后经由学者研究发现该方法可同时用于造波和消波。其基本原理是在数值水槽的前端和后端分别设立一个造波区和消波区，相当于在计算区域添加进口和出口边界条件，进口边界条件只负责造波，而出口边界条件只负责消波。造波区和消波区内每一时刻对速度进行解析松弛处理，保证波浪在数值水槽中传播时不受二次反射波以及透射波的影响。本文在对速度解析松弛处理基础上，对Level-Set函数φ也作同样处理。

解析松弛处理的关系式为

(13)

式中下标r，a，c分别代表解析松弛值、理论值以及当前计算值。

式(13)中的R(x)为解析松弛函数，本文选取Jacobsen提出的松弛函数，表达式为

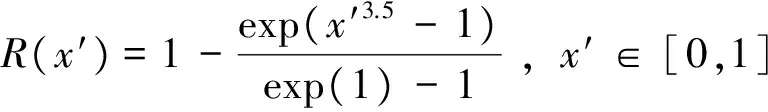
(14)

式中x′为造波区或消波区内水平方向坐标与造波区或消波区长度的比值。一般在造波区内解析松弛函数取R(x′)，消波区内取R(1-x′)。

图1 潜堤上波浪传播数值水槽模型示意图Fig.1 Schematic diagram of numerical flumemodel for simulating wave propagation overa submerged dike

3 算例验证

为验证第2节数值模型对潜堤上波浪传播过程数值模拟的精确性，本文选取Beji等[16]建立的潜堤上波浪传播过程物理试验模型作为算例，图1为物理试验模型简化成的潜堤上波浪传播数值水槽模型。

整个数值水槽长38.0m，高0.80m，水槽中水位为0.40m。造波区和消波区分别位于数值水槽的前后两端，梯形潜堤位于数值水槽中部的工作区。波浪由造波区生成后从左向右传播至工作区，经过潜堤后最终进入消波区。梯形潜堤的前沿距造波区6.0m，向波坡面坡度1∶20，背波坡面坡度1∶10，潜堤高度0.30m，数值水槽中水位距潜堤顶部0.10m。水槽工作区内共设置8个水位仪用于水位监测，分别为WG1—WG8，以造波区为起点，对应位置分别为6.0，11.0，12.0，13.0，14.0，15.0，16.0，17.0m。数值模拟网格大小dx=dz=0.01 m，整个数值水槽网格单元数为304 000。为模拟试验中的真实波浪，本文选取周期T=2.525 s，波高H=0.022 m的二阶Stokes波为生成波。时间步大小满足CFL条件：CFL数=0.1。

将水位仪(WG1—WG8)所处位置的波浪水位数值计算结果与Beji等[16]的试验结果进行对比，结果如图2所示。

图2 潜堤上波浪传播过程中水位数值计算与试验结果的对比Fig.2 Comparison between numerical results and experimental data of water level in the process of wave propagation over a submerged dike

图2表明：

(1) 图2(a)中水位仪WG1监测的是波浪传播至潜堤向波坡面起点的水位。由于潜堤向波坡面的存在，波浪从深水区往浅水区传播过程中受到浅水作用而出现变形。WG1数值计算水位波形水平方向不对称并且波峰高度比波谷深度要稍微大一点。

(2) 图2(b)中水位仪WG2监测的是波浪传播至潜堤向波坡面上的水位。WG2计算水位波形与WG1类似，但波峰高度和波谷深度都有增加，其中波峰高度增加更为明显。

(3) 图2(c)中水位仪WG3监测的是波浪刚刚传播至潜堤顶部平台时的水位。WG3数值计算水位波形较WG2而言，波峰高度和波谷深度稍微增加，同样波峰高度增加更加明显。

(4) 图2(d)中水位仪WG4监测的是波浪沿潜堤平台传播时的水位。WG4数值计算水位波形的主波峰之后出现了2次波峰，并且主波峰高度较WG3进一步增加。

(5) 图2(e)中水位仪WG5监测的是波浪刚刚从潜堤顶部平台传播至背波坡面位置时的水位。WG5数值计算水位较WG4变化明显，出现明显的2次波峰且主波峰高度达到最大值。

(6) 图2(f)和图2(g)中水位仪WG6和WG7监测的是波浪传播至背波坡面上的水位。值得注意的是，由于潜堤背波坡面的存在，此后波浪从浅水区往深水区传播并受到反浅水作用，使得WG6和WG7数值计算水位波形出现了3次波峰，WG7的3次波峰高度较WG6要高。

(7) 图2(h)中水位仪WG8监测的是波浪传播至潜堤背波坡面终点时的水位。WG8数值计算水位波形中3次波峰高度较WG7进一步增加。

整个数值计算的各个水位监测点的水位波形与Beji等[16]的试验结果非常相符，表明本文建立的数值模型对潜堤上波浪传播过程的模拟具较高精度。

4 各种参数对波浪传播的影响

为进一步研究潜堤上波浪的传播过程，通过调整波浪波高、潜堤上淹没深度、潜堤向波坡面坡度以及背波坡面坡度等参数，深入分析各种参数对波浪传播的影响。

4.1 波浪波高

图3给出了波高H=0.011，0.022，0.044 m条件(其余计算条件与第3节一致)下潜堤上波浪传播过程中水位的数值计算结果。

图3 不同波高条件下潜堤上波浪传播过程中水位的数值计算结果Fig.3 Numerical results of water level in the process of wave propagation over a submerged dike in the presence of varying wave height

从图3中可以看出，不同波高条件下WG2，WG3，WG5，WG7数值计算水位波形明显不同，具体表现为：①由于从深水区往浅水区传播过程中波浪受到浅水作用，波高H=0.044 m的波浪受浅水作用影响较大，WG2位置波高H=0.044 m的水位波形水平方向不对称较为明显，且波峰高度和波谷深度都近似与H=0.011，0.022 m的数值计算结果成倍数关系。②WG3位置波高H=0.044 m的水位波形波峰高度进一步增加，且波形有2次波峰出现，相比之下波高H=0.011，0.022 m波峰高度增加得并不明显，波形变化较小。③WG5位置波高H=0.044 m的水位波形已出现明显的2次波峰，波浪主波峰高度明显下降。波高H=0.022 m的水位波形出现明显的2次波峰，H=0.011 m水位波形有2次波峰出现的趋势。④WG7位置波浪受反浅水作用，波高H=0.044 m水位波形明显出现3次甚至4次波峰，H=0.022 m水位波形出现明显的3次波峰，H=0.011 m水位波形有3次波峰出现的趋势。

图4 不同淹没深度条件下潜堤上波浪传播过程中水位的数值计算结果Fig.4 Numerical results of water level in the process of wave propagation over a submerged dike in the presence of varying submergence depth

4.2 潜堤顶部淹没深度

图4给出了潜堤顶部淹没深度d=0.05，0.1，0.2 m条件(其余计算条件与第3节一致)下潜堤上波浪传播过程中水位的数值计算结果。

从图4中可以看出，不同淹没深度条件下WG2，WG3，WG4，WG6数值计算水位波形明显不同，具体表现为：①由于从深水区往浅水区传播过程中波浪受到浅水作用，淹没深度d=0.05 m时波浪受浅水作用影响较大，WG2位置淹没深度d=0.05 m的水位波形水平方向不对称较为明显，且波峰高度和波谷深度均比d=0.1，0.2 m的数值计算结果要大。值得注意的是，淹没深度d=0.05 m条件下波浪传播的水平速度要更大。②WG3位置淹没深度d=0.05 m的水位波形波峰高度进一步增加，且波形有2次波峰出现，相比之下d=0.1，0.2 m波峰高度增加的并不明显，波形变化较小。③WG4位置淹没深度d=0.05 m的水位波形已出现明显的2次波峰，波浪主波峰高度明显下降。淹没深度d=0.1 m的水位波形也有明显的2次波峰出现，d=0.2 m水位波形变化不大。④WG6位置淹没深度d=0.05 m的水位波形受反浅水作用，出现3次甚至4次波峰。淹没深度d=0.1 m水位波形的2次波峰高度明显增加并出现3次波峰，d=0.2 m水位波形有2次波峰出现趋势。

4.3 潜堤向波坡度

图5给出了潜堤向波坡度1∶5，1∶10，1∶20条件下(其余计算条件与第3节一致)潜堤上波浪传播过程中水位的数值计算结果。

图5 不同向波坡度条件下潜堤上波浪传播过程中水位的数值计算结果Fig.5 Numerical results of water level in the process of wave propagation over a submerged dike with varying seaward slope gradient

从图5中可以看出，不同向波坡度条件下WG2，WG3数值计算水位波形明显不同，而WG5，WG6水位波形近乎相同。其中，从深水区往浅水区传播过程中波浪受到浅水作用，向波坡度1∶20时波浪受浅水作用影响较大，WG2与WG3位置水位波形水平方向不对称较为明显，波峰高度增加较多。值得注意的是，淹没深度d=0.05 m条件下波浪传播的水平速度要更大；相比之下坡度1∶5，1∶10的水位波形变化不明显，波峰高度有些许增加。由于后续潜堤的水平平台尺寸以及背波坡度都一致，波浪的后续传播过程中外部条件影响相同，导致后续水位波形趋于相同。

4.4 潜堤背波坡度

图6给出了潜堤背波坡度1∶5，1∶10，1∶20条件下(其余计算条件与第3节一致)潜堤上波浪传播过程中水位的数值计算结果。

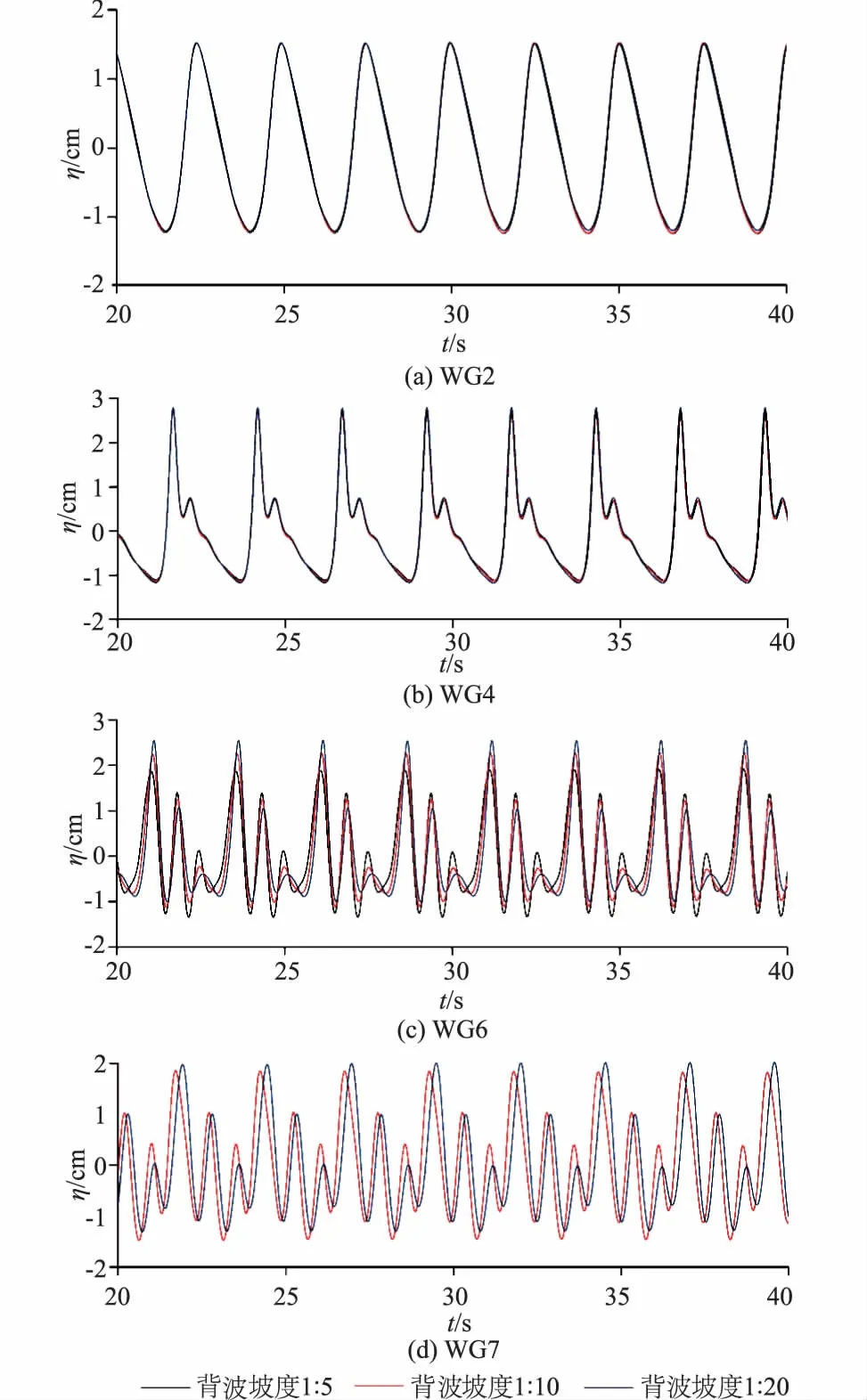
图6 不同背波坡度条件下潜堤上波浪传播过程中水位的数值计算结果Fig.6 Numerical results of water level in the process of wave propagation over a submerged dike with varying leeward slope gradient

从图6可以看出，不同背波坡度条件下WG2，WG4数值计算水位波形几乎一致，而WG6，WG7水位波形有些许不同。其中，由于潜堤的向波坡度以及水平平台尺寸都一致，波浪的前期传播过程中外部条件影响相同，导致WG2，WG4数值计算水位波形几乎一致。后续波浪从浅水区往深水区传播过程中波浪受到反浅水作用，从图6(c)，图6(d)中可以看出，背波坡度1∶20条件下受反浅水作用稍大，WG6，WG7水位波形水平方向不对称稍微明显。但总体来说，3种背波坡度条件下波浪受反浅水作用影响较为接近，WG6，WG7位置水位波形主波峰、2次及3次波峰高度相差不大。由于背波坡度1∶5条件下，WG7位置不在背波坡面上，所以背波坡度1∶5的WG7水位波形不参与比较。

5 结 论

本文从进一步提升潜堤上波浪传播数值模拟的精度出发，利用五阶WENO有限差分格式以及三阶TVD Runge-Kutta格式离散求解RANS方程，采用Level-Set方法追踪波浪与空气间自由面并采用解析松弛法实现造波消波，建立了一种求解潜堤上波浪传播问题的数值模型。采用经典的梯形潜堤试验验证数值模型精度，并进一步研究了波高、潜堤顶部淹没深度以及潜堤坡度等参数对潜堤上波浪传播过程的影响，得到以下结论：

(1) 数值模型计算的各个水位监测点的水位波形与Beji等[16]的试验结果非常相符，表明数值模型对潜堤上波浪传播过程的模拟具有较高的精度，数值模拟结果具有较高的可靠性。

(2) 波高越高时波浪受浅水作用越明显，波浪变形较为明显，水位波形较早出现次级波峰；波高H=0.044 m条件下，水位波形甚至出现了4次波峰。

(3) 潜堤的淹没深度越小波浪受浅水作用越明显，此时波浪变形非常明显；淹没深度d=0.05 m条件下，水位波形同样出现了4次波峰。

(4) 潜堤的向波坡面越小，浅水作用越明显；而背波坡面坡度越小，受反浅水作用稍大，但并不明显。

[1] BROCCHINI M, DRAGO M, IOVENITTI L. The Modelling of Short Waves in Shallow Waters. Comparison of Numerical Methods based on Boussinesq and Serre Equations[C]∥American Society of Civil Engineers. Proceedings of the 23rd International Conference on Coastal Engineering. Venice, Italy. October 4-9, 1992: 76-88.

[2] BEJI S, BATTJES J A. Numerical Simulation of Nonlinear Wave Propagation over a Bar[J]. Coastal Engineering, 1994, 23(1): 1-16.

[3] 孙 先, 杨文俊, 王国栋. 基于 坐标变换和水位函数法的立面二维水动力学模型[J]. 长江科学院院报, 2012, 29(7): 6-9, 26.

[4] KOBAYASHI N, OTTA A, ROY I. Wave Reflection and Run-up on Rough Slopes[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1987, 113(3): 282-298.

[5] 陈善群, 廖 斌, 李海峰. 用最小二乘无网格有限差分方法求解二维浅水方程[J]. 长江科学院院报, 2012, 29(6): 36-39, 57.

[6] 李昌良, 谢媛媛. 不同结构形式潜堤上的随机波浪运动[J]. 海岸工程, 2008, 27(1): 1-9.

[7] 蒋昌波, 曹永港, 陈 杰, 等. 斜坡上梯形潜堤附近流动结构的数值研究[J]. 水动力学研究与进展A辑, 2009, 24(3): 286-295.

[8]JACOBSEN N G, FUHRMAN D R, FREDSØE J. A Wave Generation Toolbox for the Open-source CFD Library: OpenFOAM[J]. International Journal for Numerical Methods in Fluids, 2011, 70(9): 1073-1088.

[9] 刘忠波, 于德海, 孙昭晨. 潜堤上破碎波浪传播变形的数值模型及其验证[J]. 海洋通报, 2011, 30(6): 633-636.[10]OSHER S,SETHIAN J A.Fronts Propagating with Curvature-dependent Speed:Algorithms based on Hamil- ton-Jacobi Formulations[J].Journal of Computational Physics, 1988, 79(1): 12-49.

[11]VAN DER VORST H A. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems[J]. SIAM Journal on Scientific and Statistical Computing, 1992, 13(2): 631-644.

[12]WILCOX D C. Turbulence Modeling for CFD[M]. Los Angeles: DCW Industries Inc., 1994.

[13]JIANG G S, SHU C W. Efficient Implementation of Weighted ENO Schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228.

[14]SHU C W, OSHER S. Efficient Implementation of EssentiallyNon-oscillatoryShockCapturingSchemes[J].Journal of Computational Physics, 1988, 77(2): 439-471.

[15]MAYER S,GARAPON A,SØRENSEN L S.A Fractional StepMethodforUnsteadyFreeSurfaceFlowwithAppli- cationstoNon-linearWaveDynamics[J].International Journal for Numerical Methods in Fluids, 1998, 28(2): 293-315.

[16]BEJI S, BATTJES J A. Experimental Investigation of Wave Propagation over a Bar[J]. Coastal Engineering, 1993, 19(1/2): 151-162.

(编辑：黄 玲)

Numerical Investigation of Wave Propagation overa Submerged Dike

LIAO Bin, CHEN Shan-qun, REN Chao-yang

(College of Civil Engineering and Architecture, Anhui Polytechnic University, Wuhu 241000, China)

In this study, a computational model is established for solving wave propagation over a submerged dike based on RANS equations combined with Level-Set method. The fifth-order finite difference WENO scheme is used for spatial discretization, and a TVD third-order Runge-Kutta explicit time scheme is employed for time discretization in the model. The Level-Set method is used for tracking the free interface between the air and water phases, and a relaxation method is employed for wave generation and absorption. In order to validate the accuracy and applicability of the model, numerical investigation of the wave propagation over a submerged dike is conducted. The numerical results show a good agreement with experimental data. Further studies are carried out to investigate the influence of physical parameters, such as wave height, submerged depth, seaward and leeward slope gradients, on the process of wave propagation over a submerged dike. Results reveal that when the wave height is higher, submerged depth smaller, and seaward slope flatter, the effect of shoaling is more obvious; when leeward slope is flatter, the effect of shoaling on wave is slightly larger, but not obvious.

submerged dike; Level-Set method; wave propagation; numerical investigation；shoaling

2016-04-25；

2016-06-16

国家自然科学基金项目(51409001)；安徽省自然科学基金项目(1508085QE100)；安徽高校优秀青年人才支持计划项目(gxyq2017015)

廖 斌(1985-)，男，江西抚州人，高级实验师，硕士，研究方向为流体力学，(电话)13515534139(电子信箱)liaobinfluid@126.com。

10.11988/ckyyb.20160393

2017,34(8):52-58

TV131.2

A

1001-5485(2017)08-0052-07