分级加载条件下深部灰岩蠕应变特性研究

肖伟晶，王晓军, b ，陈 辰，卓毓龙，李永欣

(江西理工大学 a.资源与环境工程学院；b.江西省矿业工程重点实验室，江西 赣州 341000)

分级加载条件下深部灰岩蠕应变特性研究

肖伟晶a，王晓军a, b，陈 辰a，卓毓龙a，李永欣a

(江西理工大学 a.资源与环境工程学院；b.江西省矿业工程重点实验室，江西 赣州 341000)

为研究深部灰岩蠕应变特性，采用GDS-VIS三轴流变仪对不同深度试样做分级加载单轴蠕变试验。基于试验结果，计算出灰岩长期强度与瞬时强度之比的均值为0.758，且深度越深比值越小；分析不同深度灰岩在各分级应力水平下轴向蠕应变增量与加载级数的变化规律，并将蠕应变增量进行一次累加，得到轴向蠕应变。结果表明：蠕应变增量随级数的增加呈现先减小后剧增的变化规律，且随深度增加，蠕应变增量达到谷底所对应的应力百分比有明显增大趋势；在分级加载过程中，随级数增加，轴向蠕应变先后呈现减速增加、等速增加和加速增加3个发展阶段；当恒载应力百分比为60%～70%时，蠕应变趋于稳定，当超过该范围后，蠕应变加速增加直至发生蠕变破坏。研究得到的这一应力百分比范围可以为识别深部灰岩是否会发生蠕变破坏提供依据。

采矿工程；深部灰岩；蠕应变特性; 单轴蠕变试验；分级加载；长期强度

1 研究背景

随着21世纪经济的快速发展，国家对资源的需求量越来越大，采矿工程不断向深部发展，同时规模不断扩大，对矿山深部岩石力学特性研究，尤其是深部岩石的流变特性研究正成为科研工作者们关注的焦点[1-7]。岩石在恒载应力作用下，其变形具有时间效应的现象称之为流变或蠕变。许多科研工作者在岩石的流变领域做了大量研究，并得出很多重大研究成果[8-10]。邵珠山等[11]基于脆性岩石细观模型，分析了岩石细观蠕变损伤特性，得出裂纹角度对脆性岩石的力学性质有重要影响；张清照等[12]对绿片岩试样做蠕变试验，得到岩样的长期强度,并提出了一种新的长期强度定量分析方法；曹平等[13]通过对金川矿区工程深部斜长角闪岩以分级增量加载方式进行松弛试验与蠕变试验，研究其流变特性并建立了流变模型；曹文贵等[14]通过模拟岩石加速蠕变的全过程，并引入损伤理论，建立了岩石加速蠕变过程中损伤模拟的新方法；蒋昱州等[15]以三峡库区典型砂岩为研究对象，研究在不同应力水平下典型砂岩的流变特性，并推导出了在三维应力状态下的流变本构方程；韩庚友等[16]对薄层状岩石做分级蠕变试验，研究岩石在不同加载方向的蠕变特性，结果表明片理面的存在对岩石蠕变曲线的影响较小；王志俭等[17]对三峡库区万州红层砂岩做流变特性试验，分析并研究了砂岩蠕变特性以及蠕变应变率随时间的变化规律。

笔者对江西某矿深部灰岩做分级加载的单轴蠕变试验并获取试验数据，通过对试验数据进行分析，研究灰岩在不同应力水平下的蠕变特征，讨论了灰岩在各应力水平下蠕应变增量以及轴向蠕应变的发展规律。

2 试验方案

选用3个不同深度，且完整性较好的灰岩进行试验，每个深度取2块，共6块。为减少选取岩石试样时的离散性导致的试验误差，采用RSM-SY(5)型分体式智能声波检测仪对各试样进行轴向声波测试，取同一深度下声波波速相近的岩样，将其加工成尺寸为Φ50 mm×100 mm圆柱形试样(在制作过程中，试样尺寸会有少许出入)。将试样两端进行打磨，使其端面不平行度和平直度控制在±0.02 mm以内。试验仪器及试样见图1，各岩石试样参数见表1。

图1 试验仪器及试样Fig.1 Test apparatuses and specimens

2.1 单轴压缩试验

采用RMT-150C岩石力学试验系统对不同埋

表1 岩石试样参数

深灰岩试样做无侧限单轴加载压缩试验，采用位移式控制加载，加载速率为0.002 mm/s，自动记录各试样单轴抗压强度，见表2。

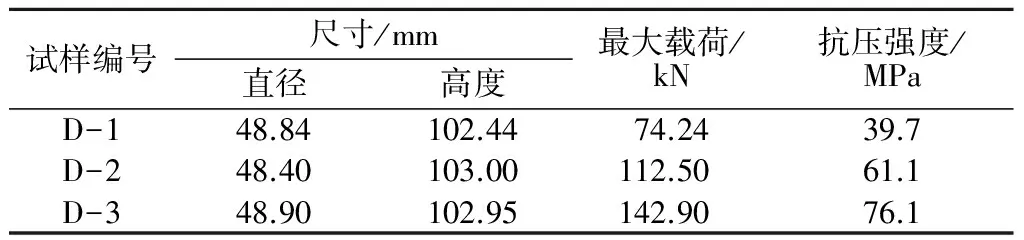
表2 岩石试样单轴试验结果

2.2 单轴蠕变试验

采用分级加载方式对试样R-1,R-2,R-3进行分级加载蠕变试验，得到不同应力水平下灰岩蠕变特性，其中各分级恒载应力值的大小参考同一深度灰岩试样的单轴抗压强度试验值σc进行设置。采用GDS-VIS三轴流变仪进行分级蠕变试验，通过应力式控制加载，加载速率为0.1kN/s，加载至指定荷载并稳压8h后，再继续加载至下一分级应力。

3 试验数据分析

3.1 蠕变特性分析

通过分级加载蠕变试验，测得各荷载水平下岩石试样的力学参数，并绘制出各试样蠕变试验特性曲线(各荷载水平加载阶段在曲线中未画出),见图2。

根据蠕变特性曲线，3个试件除最后一级恒载出现加速蠕变外，其余各分级均未出现。而且在发生蠕变破坏前一分级(即倒数第二分级)出现等速蠕变，但蠕变速率为一个很小的定值且几乎为0，由此取蠕变破坏前一分级(即倒数第二分级)应力值作为长期强度[6, 16]，据此，各试样的长期强度所对应的荷载分别为56,84,108kN。计算各试样的长期强度σ，取相同深度下试样的单轴抗压强度为该试样的瞬时强度σi，计算出σ与σi的比值μ，见表3。

表3 长期强度与瞬时强度比值

由表3可知，该矿深部灰岩的长期强度与瞬时强度之比的平均值为0.758，且随深度增加，比值呈逐渐减小的趋势。根据文献[6]，由经验统计得到长期强度与瞬时强度之比的范围为0.60～0.80时，蠕变特性较强，据此可知，该矿深部灰岩具有较强的蠕变特性，且深度越深，蠕变特性越强。

3.2 蠕应变特性分析

根据分级加载蠕变试验结果，得到各试样在不同荷载作用下轴向应变的变化情况，其中，各荷载水平恒载状态下产生的应变称之为蠕应变增量[18]，其计算公式为

(1)

式中：Δεc表示蠕应变增量；usc,uec分别是开始蠕变时的变形和蠕变结束时的变形；h为试样高度。计算结果见表4。应力百分比为各分级应力与单轴抗压强度比值。

表4 不同荷载下轴向蠕应变增量

根据表4，绘制出各试样在整个蠕变过程中，各轴向蠕应变增量变化趋势,见图3。

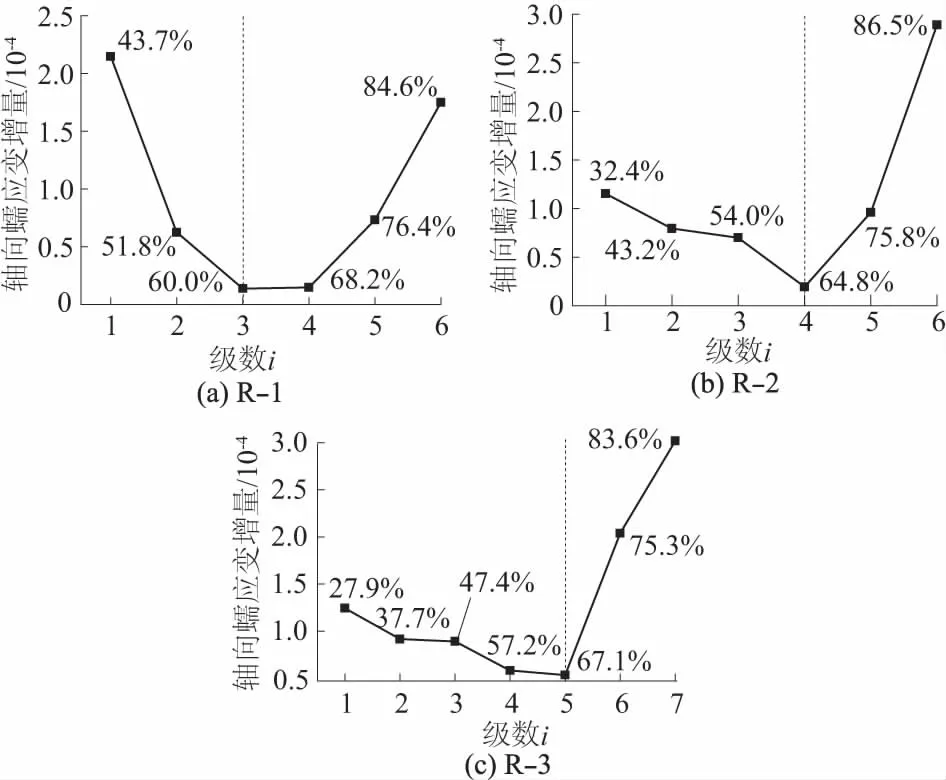
注：百分数表示各点的应力百分比图3 轴向蠕应变增量与级数的关系Fig.3 Relationship between increment of axial creep strain and load step

由图3可知：在蠕变试验过程中，随着各分级恒载应力的增加，各分级蠕变应变增量呈现先减小后增加的发展趋势。而且与前期减小的趋势相比，后期蠕应变增量随应力百分比增加而增加的趋势更加明显，直至试样最终发生蠕变破坏。

通过进一步分析可知，由于岩石试样在未受荷载前，内部含有一定数量的空隙，在前期荷载下空隙被明显压密，轴向蠕应变增量较大，而且随着级数增加，应力百分比增大，空隙逐渐密实，轴向蠕应变增量减小；当试样内部空隙被充分压密后，随着恒载应力继续增加，空隙裂隙开始相互贯通，蠕应变增量不再减小，而是逐渐增大，内部损伤持续发展，直至试样发生蠕变破坏。根据图3可知，3个试样随深度增加，轴向蠕应变增量达到谷底时所对应的级数越来越高，应力百分比越来越大，依次为60.0%,64.8%,67.1%，据此可得出，该矿深部灰岩随深度增加，轴向蠕应变增量达到谷底所对应的应力百分比有明显后移趋势。说明随深度增加，压密岩石所需要的应力水平逐步增高。

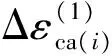
(2)

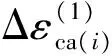
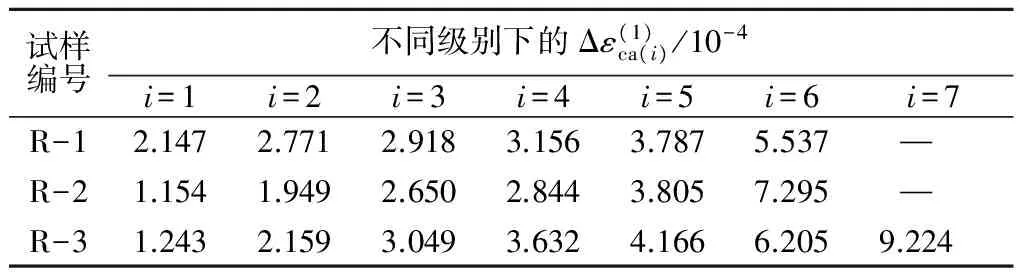
表5 各分级轴向蠕应变

结合表5，绘制各试样在不同应力百分比的情况下轴向蠕应变的变化关系，如图4所示。

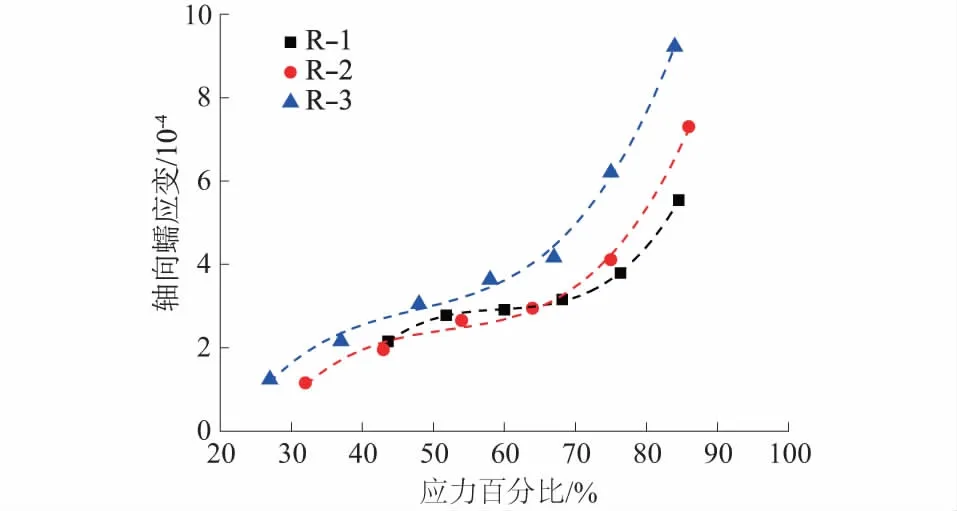
图4 轴向蠕应变与应力百分比的关系Fig.4 Relationship between axial creep strain and stress

通过分析图3和图4可知，在蠕变试验过程中，随恒载应力百分比的增加，轴向蠕应变呈现减速增加、等速增加和加速增加3个发展阶段。表明在蠕变试验前期，随各分级恒载应力百分比的增加，试样内部原有的空隙被逐渐压密，轴向蠕应变增量逐级递减，轴向蠕应变则呈现减速增加和等速增加。在蠕变试验后期，蠕应变拟合曲线等速阶段与加速阶段的拐点所对应的应力百分比在60%～70%之间，在此应力范围内，岩石试样内部已充分压密，空隙裂隙稳定发展；当恒载应力百分比超过该范围并继续增加时，空隙裂隙相互贯通，内部损伤不断发展，致使轴向蠕应变加速增加，直至试样发生蠕变破坏。各稳定状态的应力区间所对应的应力与长期强度比值的范围见表6。

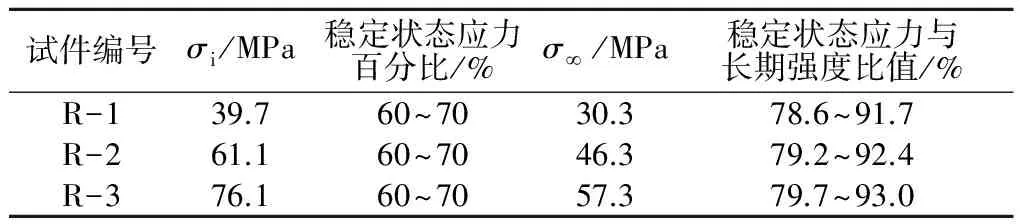
表6 各稳定状态应力与长期强度的比值

由表6可知，当岩体处于稳定状态时所对应的应力与长期强度的比值在78.6%～93.0%之间，且随深度增加，该比值逐步提高(3个不同深度试样的比值范围依次为：78.6%～91.7%,79.2%～92.4%,79.7%～93.0%)。由此可将该稳定状态应力区间作为长期强度的初步判别范围。

上述分析表明：当应力百分比在 60%～70%之间时，该矿深部灰岩被充分压缩密实，岩体处于稳定状态，此时岩体所受应力与长期强度的比值在78.6%～93.0%之间；当应力百分比超过该范围后，蠕应变将明显增加，最终导致蠕变破坏。根据研究得到的这一应力百分比范围可以为识别该矿深部灰岩是否会发生蠕变破坏提供依据，同时也能够为初步判别岩体长期强度提供参考。

4 结 论

(1) 该矿深部不同深度灰岩的长期强度与瞬时强度的比值μ依次是0.764,0.758,0.753，均值为0.758，而且深度越深,比值越小。由此表明，该矿深部灰岩的蠕变特性较为明显，且随深度增加蠕变特性增强。

(2) 在各分级应力的恒载作用下，灰岩蠕应变增量随级数(或恒载应力)的增加呈现先减小后剧增的趋势。随深度增加，轴向蠕应变增量达到谷底时的级数越来越高，所对应的应力百分比有明显后移趋势。说明随深度增加，压密岩石所需要的应力水平逐步增高。

(3) 在蠕变过程中，随应力百分比增加，轴向蠕应变先后呈现减速增加、等速增加和加速增加3个发展阶段。当应力百分比为60%～70%时，灰岩试样轴向蠕应变只出现减速增加和等速增加，岩体处于稳定状态；当超过该范围后，轴向蠕应变将急剧增加，最终发生蠕变破坏。因此，研究得到的这一应力百分比范围可以为识别该矿深部灰岩是否会发生蠕变破坏提供依据。

[1] 孙 钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报,2007,26(6):1081-1106.

[2] 蒋海飞,胡 斌,刘 强,等. 一种新的岩石黏弹塑性流变模型[J]. 长江科学院院报,2014,31(7):44-48.

[3] 张 哲,王大国,洪 林. 深部岩体中断续节理对巷道稳定性影响的数值试验[J]. 辽宁工程技术大学学报,2007, 26(4):481-484.

[4] 周宏伟,谢和平,左建平. 深部高地应力下岩石力学行为研究进展[J]. 力学进展,2005,35(1):91-99.

[5] 胡 波,王宗林,梁 冰,等. 岩石蠕变特性试验研究[J]. 实验力学,2015,30(4):438-446.

[6] 刘传孝,贺加栋,张美政,等. 深部坚硬细砂岩长期强度试验[J]. 采矿与安全工程学报,2010,27(4):581-584.

[7] 王志荣,张利民,韩中阳. 平顶山盐田互层状盐岩蠕变特性与试验模型研究[J]. 水文地质工程地质,2014,41(5):125-130,137.

[8]AYDANO,AKAGIT,KAWAMOTOT.TheSqueezingPotentialofRockAroundTunnels:TheoryandPredictionwithExamplesTakenfromJapan[J].RockMechanicsandRockEngineering, 1996, 29(3): 125-143.

[9] 宋勇军,雷胜友,邹 翀,等. 分级加载下炭质板岩蠕变特性的试验研究[J]. 长江科学院院报,2013,30(9):47-52.

[10]MALANDF.Time-dependentBehaviorofDeepLevelTabularExcavationsinHardRock[J].RockMechanicsandRockEngineering, 1999, 32(2): 123-155.

[11]邵珠山, 李晓照. 基于细观力学的脆性岩石蠕变损伤特性研究[J]. 固体力学学报,2015,36(增1):44-49.

[12]张清照,沈明荣,丁文其. 锦屏绿片岩力学特性及长期强度特性研究[J]. 岩石力学与工程学报,2012,31(8):1642-1649.

[13]曹 平,郑欣平,李 娜,等. 深部斜长角闪岩流变试验及模型研究[J]. 岩石力学与工程学报,2012, 31(增1):3015-3021.

[14]曹文贵,袁靖周,王江营,等. 考虑加速蠕变的岩石蠕变过程损伤模拟方法[J]. 湖南大学学报(自然科学版),2013,40(2):15-20.

[15]蒋昱州,王瑞红,朱杰兵,等. 砂岩的蠕变与弹性后效特性试验研究[J]. 岩石力学与工程学报,2015,34(10):2010-2017.

[16]韩庚友,王思敬,张晓平,等. 分级加载下薄层状岩石蠕变特性研究[J]. 岩石力学与工程学报,2010,29(11):2239-2247.

[17]王志俭,殷坤龙,简文星,等. 三峡库区万州红层砂岩流变特性试验研究[J]. 岩石力学与工程学报,2008,27(4):840-847.

[18]潘金龙,王 俊,刘伟庆,等. 大气或氯离子浸泡环境下玻璃纤维增强复合材料蠕变试验和理论研究[J]. 工业建筑,2015,45(4):127-131.

(编辑：占学军)

Creep Strain Characteristics of Deep Limestone under Step Loading

XIAO Wei-jing1, WANG Xiao-jun1, 2, CHEN Chen1, ZHUO Yu-long1, LI Yong-xin1

(1.School of Resource and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China; 2.Jiangxi Provincial Key Laboratory of Mining Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China )

In the aim of exploring the creep characteristics of deep limestone, uniaxial creep tests were conducted with GDS-VIS triaxial rheometer by step loading on specimens from different depths. According to the test results, the mean value (0.758) of the ratio of long-term strength to instantaneous strength decreases as depth increases. Furthermore, the variation law of axial creep strain increment of limestone in different depths under different stress levels was investigated, and then axial creep strains were obtained by accumulating creep strain increment. Results revealed that creep strain increment decreased first and then increased dramatically with the increasing of stress level. As depth increased, the percentage of stress corresponding to the minimum creep strain increment obviously increased. Moreover, with the increase of loading level, the axial creep strain experienced three development stages from decelerated growth, constant growth and accelerated growth. When the stress percentage ratio of constant load was within the range from 60% to 70%, creep strain tended to be stable; whereas beyond the range, the creep strain acceleratedly increased until creep failure. Therefore, the range of stress percentage could be taken as reference for identifying whether creep failure will happen or not for deep limestone.

mining engineering; deep limestone; creep strain characteristics; uniaxial creep test; step loading; long-term strength

2016-07-31；

2016-09-07

国家自然科学基金项目(51564012)；江西省科技支撑计划项目(20141BBE50005)

肖伟晶(1991-)，男，江西高安人，硕士研究生，主要从事工程岩体稳定性分析与控制等方面的研究工作，(电话)18270716918(电子信箱)921046160@qq.com。

王晓军(1979-)，男，山西晋中人，副教授，博士，从事工程岩体稳定性分析与控制等方面的研究与教学工作,(电话)13970141616(电子信箱)xiaojun7903@126.com。

10.11988/ckyyb.20160767

2017,34(8):135-138，143

TD315

A

1001-5485(2017)08-0135-04