明渠曲线渐变段体型求解新方法研究

邬 颢，刘韩生，金 硕

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

明渠曲线渐变段体型求解新方法研究

邬 颢，刘韩生，金 硕

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

明渠渐变段体型对渐变段中的水流形态有很大影响。为了解决明渠渐变段与下游水流的扩散衔接问题，消除明渠渐变段下游菱形冲击波的影响，根据冲击波特性和辐射水流基本关系，采用冲击波简化积分式，并考虑到渐变段水流与下游衔接，按刘韩生曲线边墙窄缝挑坎计算方法算出明渠曲线渐变段边墙体型，且该方法能够计算渐变段中的水面线。试验表明明渠曲线渐变段中水流平顺稳定且水面渐变升高。渐变段后水流正常，为均匀流，无菱形冲击波的影响，故能够解决水流扩散衔接的问题，该方法可以运用到明渠曲线渐变段边墙体型设计中。

明渠；渐变段；冲击波；边墙体型；水面线

1 研究背景

渐变段是明渠水流常用的水工建筑物,渐变段体型主要有直线型和曲线型2种。曲线型渐变段中水流相较直线型[1]更平顺稳定，与渐变段下游渠道水流衔接更好，众多学者对其进行了深入研究。20世纪90年代，刘韩生等[2-6]应用冲击波简化积分式直接推导曲线反射扰动线的方程而无需迭代试算，进行了曲线边墙窄缝挑坎设计。丙巷河水库枢纽泄洪隧洞出口[7]应用了该方法，经水力学模型试验验证，效果很好，能较好适应山区狭窄河谷高水头的水库枢纽泄洪消能布置。

根据冲击波简化积分式设计窄缝挑坎与设计明渠渐变段在本质上是相同的，不同之处在于窄缝挑坎的设计主要考虑到挑坎的泄流要求[3]，边墙曲线只需保留图1中A0M段，自M点经挑坎挑射出流；而明渠渐变段的设计主要考虑渐变段水流与下游的平顺衔接问题，故需添加图1中B0M段。

图1 曲线边墙渐变段计算模型Fig.1 Calculation model of the transition section with curved side-wall

窄缝挑坎设计方法是根据冲击波理论推导得出，冲击波理论是广泛适用于解决明渠水力问题的基本方法，同样可以运用在明渠曲线渐变段体型设计中。

2 计算方法

计算方法参见文献[3]。

2.1 曲线边墙的确定

类似于曲线边墙窄缝挑坎，明渠曲线边墙渐变段可看作边墙连续的微小转折[8]，产生的冲击波为缓冲击波，适合比能不变假定，不考虑能量损失[9]，渠道做成平底渠道。渐变段断面为矩形，来流为均匀流，已知渠道设计流量Q，控制渐变段进口断面的水深为h1，渐变段前渠道宽b1，渐变段后渠道宽b2。则可求出渐变段进口断面的流速v1及Fr12(Fr1为进口断面的弗劳德数)。

根据刘韩生对称曲线边墙窄缝挑坎的计算方法，水流比能H为

(1)

式中h,v分别代表渐变段中任一断面的水深和流速。

冲击波简化积分式[2]为

(2)

式中α为曲线边墙上任一点处的切线方向与来流流向的夹角，单位为弧度。该式反映了曲线边墙水面线的变化规律。

辐射水流基本关系为：

(3)

(4)

式中：Fr0,Fr分别为已知点、待求点的弗劳德数；R0,R分别为已知点、待求点的辐射半径；P为设定的函数名。

由水流连续条件、比能不变假定及辐射水流基本关系推导得到渐变段出口断面的水深h2及Fr22(Fr2为出口断面的弗劳德数)。

渐变段长度L为

(5)

式中α0为收缩角的一半(图1)。α0满足式(6)

(6)

P0点和Q0点的辐射半径分别为：

(7)

(8)

图1中，规定以渐变段进口断面与中轴线的交点为坐标原点，中轴线为x轴，正方向为水流流向。由上述公式得到渐变段边墙A0点与B0点的坐标分别为(xA0，yA0),(xB0，yB0)。

取α=α0，由式(9)可得M点的坐标，即

(9)

式中RM,FrM分别为M点的辐射半径和弗劳德数。

特征线的性质[10]及辐射水流的基本关系式为：

(10)

(11)

(12)

式中：FrAi,FrPi分别为Ai点和Pi点的弗劳德数;RPi,RP0分别为Pi点和P0点的辐射半径。

由式(10)—式(12)可得A0M段边墙各点Ai坐标。

为使渐变段水流与下游明渠平顺衔接，在A0M段基础上添加图1中B0M段。在B0M段，同理可求得边墙各点Bi坐标。由上述可得曲线渐变段边墙体型(如图1)。

2.2 理论水面线的确定

由于渐变段为对称曲线边墙，故渐变段左边墙与右边墙的理论水面线相同。边墙A0M段各点理论水深由式(1)和式(2)得出，B0M段各点理论水深由式(1)和式(10)得出。坐标规定同上理论所述，作出理论水面线,如图2(a)和图2(b)中虚线所示。

图2 不同部位的水面线Fig.2 Water surface lines at different positions

中轴线上的理论水深计算时分为3段:第1段为从渐变段进口至P0点，中轴线在扰动线A0P0上游，其水深不受边墙收缩的影响，保持渐变段进口水深h1；第2段为P0Q0，中轴线位于辐射水流区，将P0Q0等分为100段，分别求出各点所对应的辐射半径R，利用辐射水流基本关系及比能不变假定，由式(1)、式(3)、式(4)得出中轴线各点水深；第3段为从Q0至渐变段出口，与第1段类似，中轴线在扰动线B0Q0下游，水深与渐变段出口水深h2相同。坐标变换与边墙相同，作出中轴线理论水面线如图2(c)中虚线所示。

3 实例验证

实例的水力条件为：流量Q=18 L/s，渐变段进口断面的渠道宽度b1=0.252 m，出口断面渠道宽度b2=0.126 m，来流为均匀流，其水深h1=0.038 m。现要求计算渐变段边墙曲线，使得下游也形成均匀流。

由已知条件可得Fr12=9.79。由上述理论可得Fr22=3.02，h2=0.089 m，试验模型渐变段长度L=85.4 cm。坐标规定与上述计算方法相同。

在渐变段上选定若干代表断面，记录各断面相应的坐标x，分别测得各代表断面左边墙、右边墙和中轴线的水深。从边墙设计数据中找出与各代表断面位置相同的坐标x，并采用上述计算方法求得各代表断面边墙与中轴线的理论水深，与实测水深相比进行误差分析，如表1。

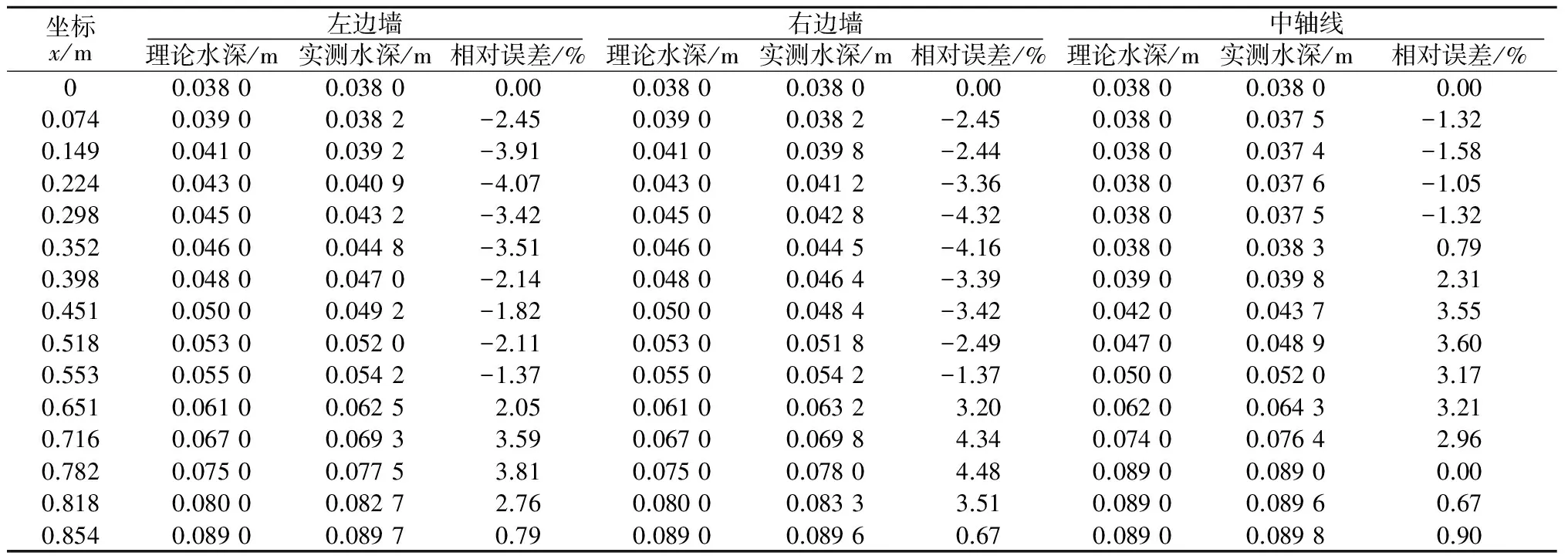
表1 不同部位理论水深与实测水深对比

误差分析结果表明，左边墙各代表断面实测水深与理论水深的误差范围为-4.07%～3.81%；右边墙各代表断面实测水深与理论水深的误差范围为-4.32%～4.48%；中轴线各代表断面实测水深与理论水深的误差范围为-1.58%～3.60%。其误差均在±5%的范围内，实测水面线满足误差要求，说明设计出的渐变段体型符合刘韩生曲线边墙窄缝挑坎的设计要求。由表1可分别作出左、右边墙及中轴线的理论水面线与实测水面线(图2)，由图2可得到水面线是逐渐变化的一条平顺曲线而并非突变，说明渐变段内水流状态较好。

图3(a)为试验中渐变段水流侧视流态，图3(b)为渐变段水流俯视流态，图3(c)为渐变段下游局部水流侧视流态。由图3(a)、图3(b)标识线可以看出渐变段中水面线为平顺曲线，急流进入渐变段后，两侧水流在中轴线交汇、扩散，逐渐消除急流冲击波的影响。由图3(c)标识线可以看出，渐变段下游已经没有冲击波的影响，不产生菱形冲击波，水面线接近水平直线，下游流态平顺稳定，说明该曲线边墙渐变段能够解决水流扩散衔接的问题。

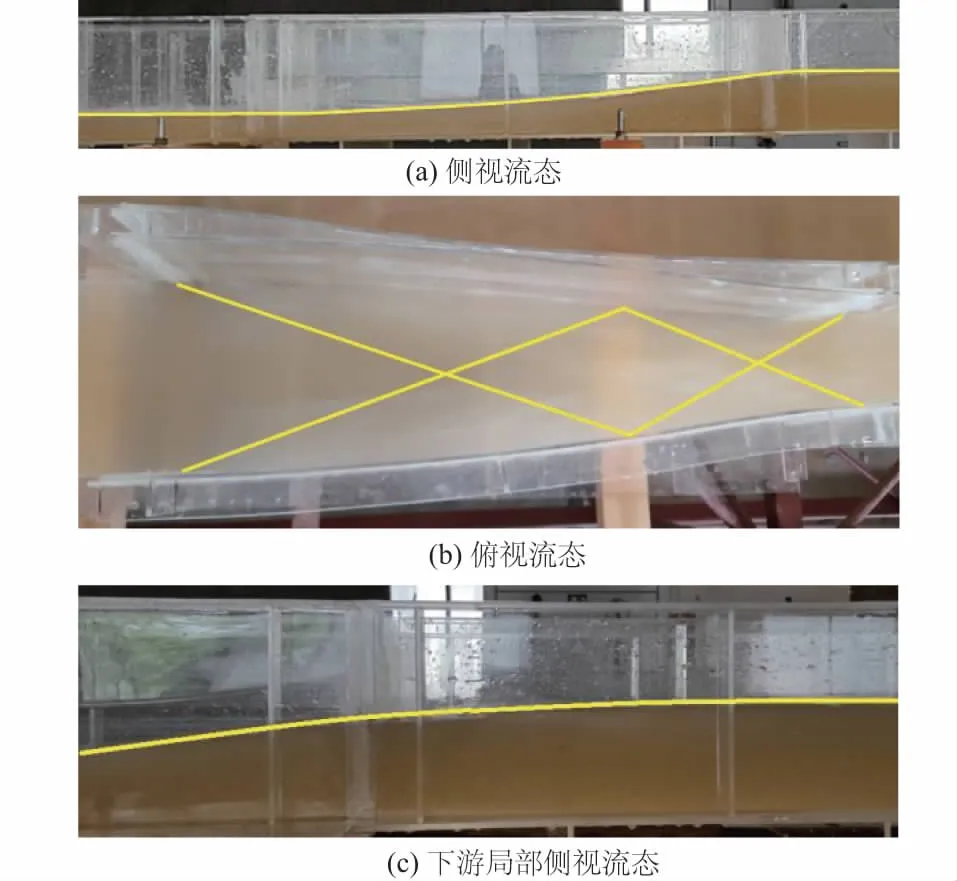
图3 渐变段不同视角下水流的流态Fig.3 Flow pattern in the transition section from different views

4 结 论

(1) 将刘韩生曲线边墙窄缝挑坎的计算方法运用到明渠曲线边墙渐变段设计中，在考虑到渐变段水流与下游衔接问题后，可以计算明渠曲线渐变段边墙体型，给出边墙曲线计算方法。

(2) 试验表明渐变段中，水流平顺稳定，水面渐变升高，渐变段后水流正常，为均匀流，无菱形冲击波的影响。

(3) 该方法能够计算水面线，理论值与实测值吻合，两者相差<5%，能够解决水流扩散衔接的问题，为工程建设提供新方法。

[1] 余常昭.明槽急变流——理论和在水工中的应用[M].北京:清华大学出版社,1999:148-153.

[2] 刘韩生,倪汉根.急流冲击波简化式[J].水利学报, 1999,30(6):56-60.

[3] 刘韩生,倪汉根,梁 川.对称曲线边墙窄缝挑坎的体型设计方法[J].水利学报, 2000,31(5):70-75.

[4] 刘韩生,倪汉根,梁 川.非对称窄缝挑坎的边墙曲线计算方法[J].水力发电学报,2001,32(3):59-67.

[5] 倪汉根,刘韩生,梁 川.兼使水流转向的非对称窄缝挑坎[J].水利学报,2001,32(8):85-89.

[6] 倪汉根,刘韩生.窄缝式消能工收缩段的体型设计[J].水利学报,1999,30(2):33-38.

[7] 张家明,陈定意.窄缝挑坎在丙巷河水库枢纽泄洪隧洞出口的设计应用[J].水力发电,2003,29(6):61-63.

[8]CHOWVT.Open-channelHydraulics[M].NewYork:McGraw-HillBookCompanyInc., 1959: 448-454.

[9] 倪汉根,刘亚坤.击波 水跃 跌水 消能[M].大连:大连理工大学出版社, 2008:1-35.

[10]斯里斯基C.M.高水头水工建筑物的水力计算[M]. 毛世民,杨立信,译.北京:水利水电出版社, 1984:113-135.

(编辑： 王 慰)

ANewMethodofCalculatingtheShapeofTransitionSectionwithCurvedSide-wallinOpenChannel

WU Hao, LIU Han-sheng, JIN Shuo

(College of Water Conservancy and Architectural Engineering, Northwest Agricultural and Forestry University, Yangling 712100, China)

The shape of transition section has great influence on the flow pattern in open channel. The aim of this research is to address the problem of flow diffusion and the coherence between transition section and downstream flow, and to eliminate the impact of diamond-shaped shock wave in the downstream of open channel. According to the characteristics of shock wave and the basic relationship between shock wave and radical flow, we calculated the shape of the transition section with curved side-wall in open channel by adopting the simplified integral equation of shock wave following Liu Hansheng’s formula of slit-bucket with curved side-wall. The flow coherence between the transition section and the downstream was also considered. This method can calculate the water surface curve in the transition section. Test results show that the flow in the transition section of open channel is smooth and stable, and water surface rises gradually. After the transition section, the water flow is normal, which is uniform flow, with no impact of diamond-shaped shock wave, demonstrating that this method could solve the problem of flow diffusion and coherence, hence can be applied to the design of transition section with curved side-wall.

open channel; transition section; shock wave; shape of side-wall; water surface curve

2016-05-16；

2016-06-21

邬 颢(1994-)，男，山东郓城人，本科生，主要从事水力学研究工作,(电话)13681929495(电子信箱)312858873@qq.com。

刘韩生(1962-)，男，陕西韩城人，教授，博士，主要从事水力学及河流动力学方面的研究工作，(电话)13319231569(电子信箱)hanshengliu@126.com。

10.11988/ckyyb.20160471

2017,34(8):68-71

TV131.3

A

1001-5485(2017)08-0068-04