多元线性回归的S P SS统计应用
——以某公司成年男子体脂率与身体形态指标为例
2017-08-31谢煊成都体育学院四川成都610041华安财产保险股份有限公司四川分公司四川成都610016
□谢煊(成都体育学院四川成都610041;华安财产保险股份有限公司四川分公司四川成都610016)
多元线性回归的S P SS统计应用
——以某公司成年男子体脂率与身体形态指标为例
□谢煊(成都体育学院四川成都610041;华安财产保险股份有限公司四川分公司四川成都610016)
本文运用多元线性回归分析方法,对某公司40名成年男子的体脂率与身体形态指标进行分析,用逐步回归方法建立线性回归方程,并与全回归结果进行对比,通过分析找出影响体脂率的主要形态指标因素。
成年男子体脂率形态指标多元线性回归应用
1、线性回归相关概念
1.1、关于“回归”一词
为了描述父母身高与儿子身高之间的关系,生物统计学家高尔顿(F.Galton,1822-1911)引进了“回归”一词。
1.2、多元线性回归模型
线性回归分析研究的是因变量与自变量的线性依存关系,多元线性回归方程为:y^=b0+b1x1+…+b k x k,其中y^为因变量y的估计值,x i(i=1,…,k)为自变量,k为自变量个数,b0为回归方程的常数项,b i(i=1,…,k)为回归系数。
一元线性回归方程在回归模型中只含有一个自变量,它是多元线性回归方程的特殊情形。
2、实例分析
某公司40名成年男子体脂率(y)与身高(x1)、体重(x2)、胸围(x3)、腰围(x4)、臀围(x5)等指标,如下表1所示。运用多元线性回归分析法的其中两种方法,即全回归分析法及逐步回归分析法及其相互间的分析对比,找出影响体脂率的主要形态指标因素。
3、全回归分析
3.1、SPSS软件操作步骤
选择“分析”菜单—“回归”—“线性(L)…”项,打开如图1所示的“线性回归”对话框,从左边的原变量列表框将因变量“体脂率”移至“因变量(D)”框,再将“身高”、“体重”、“胸围”、“腰围”、“臀围”等自变量全部移至“自变量(I)”框。在“方法(M)”下拉式列表框中选择“进入”。
图1 线性回归对话框
单击“统计量(S)…”按钮,打开“线性回归:统计量”对话框,如图2所示。在“回归系数”框中选择“估计(E)”项,在“残差”框中选择“Dur b in-W atson”项,在其他选项中选择“模型拟合度(M)”和“共线性诊断(L)”,其余使用默认选项。回到“线性回归”对话框,按“确认”按钮,进行S P SS运算。
单击“统计量(S)…”按钮,打开“线性回归:统计量”对话框,如图2所示。在“回归系数”框中选择“估计(E)”项,在“残差”框中选择“Dur b in-W atson”项,在其他选项中选择“模型拟合度(M)”和“共线性诊断(L)”,其余使用默认选项。回到“线性回归”对话框,按“确认”按钮,进行S P SS运算。
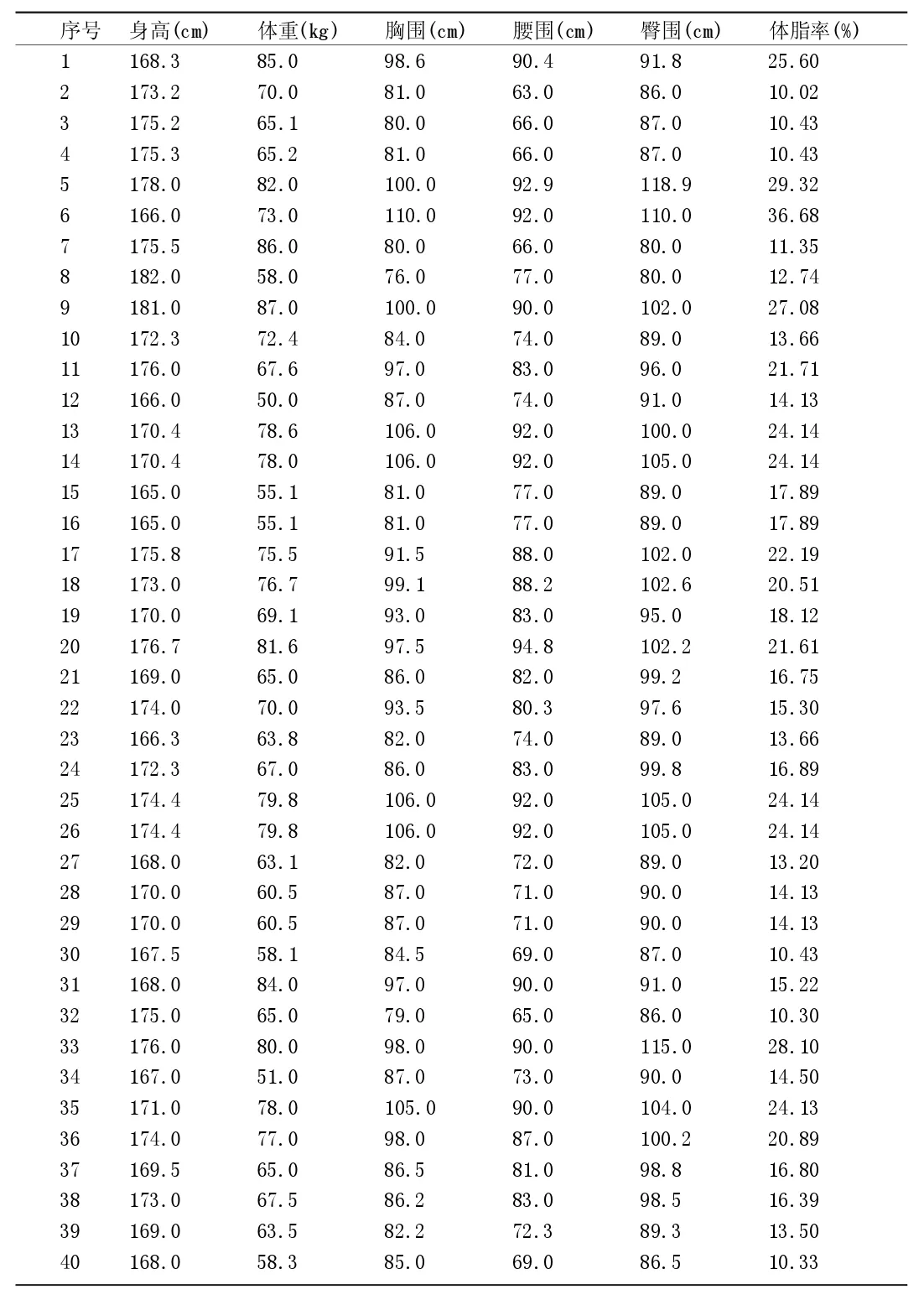
表1 某公司40名成年男子形态指标汇总表
3.2、计算结果及分析
计算结果如表2至表5所示。
表2给出了回归分析的常用统计量,其中包含了D-W检验值。决定系数R2为0.841,较接近于1;剩余标准差S y为2.69701,经计算,标准剩余标准差S y'为14.93%,精度低;D-W检验值为1.165,其值趋向于2,则说明不存在自相关关系,即不能认为存在异方差。
图2 “线性回归:统计量”对话框

表2模型汇总b
表3是对方程进行方差分析检验的结果,P<0.001,方程具有显著的可靠性,线性关系可以确立。

?
表4给出方程系数、系数检验结果和共线性检验结果。由各自变量的标准回归系数可以看出,胸围(x3)、腰围(x4)、臀围(x5)等三项指标对体脂率(y)的影响最大。通过对各自变量回归系数的t值大小的比较,也可以分析出胸围(x3)、腰围(x4)、臀围(x5)等三个自变量对体脂率(y)的影响最大。参数检验结果显示,只有b3、b4、b5的相伴概率P<0.1具有显著意义,其余系数均P>0.1,不显著。根据容忍值(T ol)法,因为T ol均大于0.1,初步说明自变量间的共线性不强。
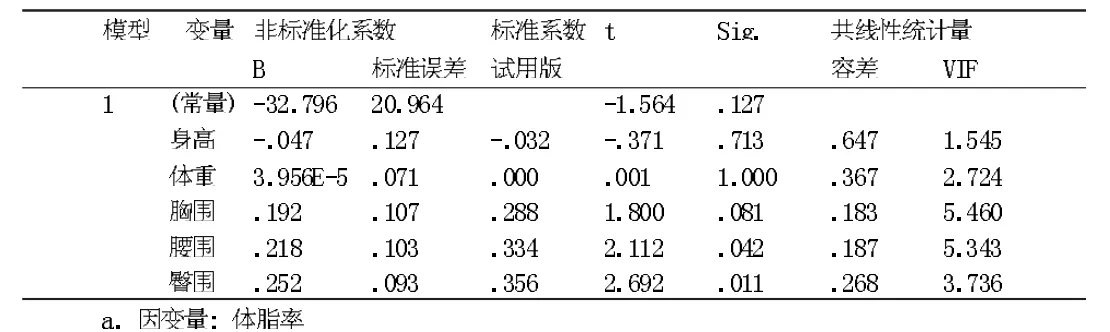
表4 系数a
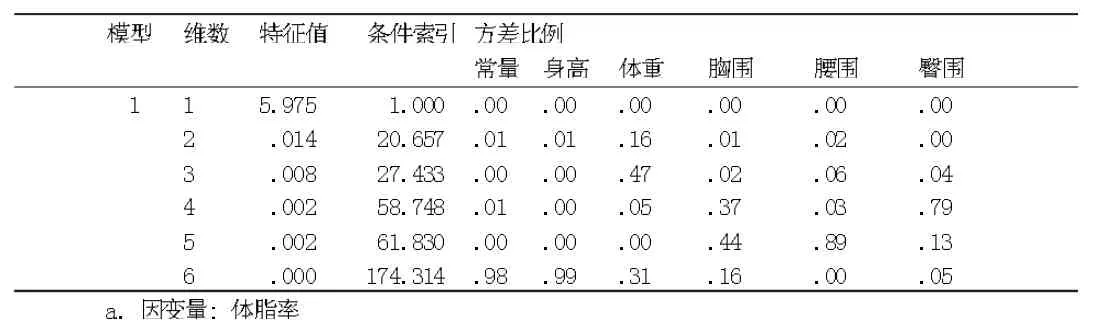
表5 共线性诊断a结果
由表4,可以得到回归方程为:
y^=-32.796-0.47x1+0.00003956x2+0.192x3+0.218x4+0.252x5
表5为共线性诊断分析结果。可以看到,第6维的条件索引为174.314,远远大于30,特征值为0,但因只有身高(x1)的方差比例(0.99)大于50%,说明这几个变量间不存在严重的共线性问题,即自变量间的共线性不强。
4、逐步回归结果与全回归结果对比分析
4.1、逐步回归分析SPSS软件操作步骤
选择“分析”菜单-“回归”-“线性(L)…”项,打开如图3所示的“线性回归”对话框,从左边的原变量列表框将因变量“体脂率”移至“因变量(D)”框,再将“身高”、“体重”、“胸围”、“腰围”、“臀围”等自变量全部移至“自变量(I)”框。在“方法(M)”下拉式列表框中选择“逐步”。
图3 线性回归对话框
在“线性回归”对话框中单击“选项”按钮,打开“线性回归:选项”对话框,如图4所示,本题采用图4的默认值。
回到“线性回归”对话框,单击“确认”按钮进行统计S P SS运算。
图4 “线性回归:选项”对话框
4.2、计算结果与全回归结果进行对比分析
计算结果如表6-表9所示。
由表6可以看出,本题的最终决定系数为0.840,与全回归决定系数0.841非常接近,且仍较接近于1;剩余标准差S y为2.62864,经计算,标准剩余标准差S y'为14.55%,虽然自变量减少,但估计精度比全回归反倒有所提高;D-W检验值为1.234,其值趋向于2,则说明不存在自相关关系,即不能认为存在异方差。
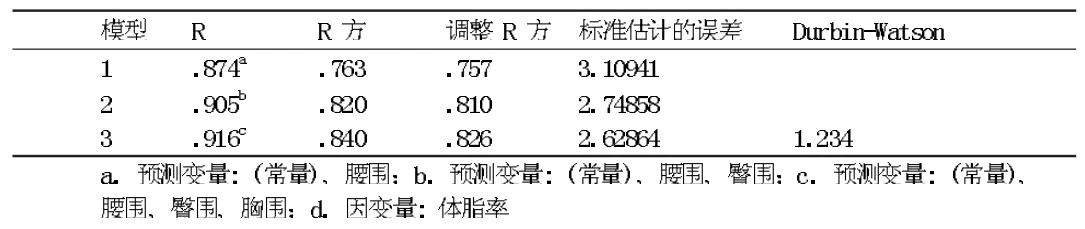
表6 模型汇总d
由表7可以看出,方差分析结果P<0.001,方程具有显著的可靠性,线性关系可以确立。
由表8可以看出,只有胸围(x3)、腰围(x4)、臀围(x5)被选入方程,其余变量均被剔除,最终得到回归方程为:
y^=-40.787+0.198x3+0.214x4+0.245x5
参数检验结果显示,目前方程中的三个自变量的P值都小于0.05,具有显著意义。共线性检验结果显示V I F<10,说明不存在共线性。
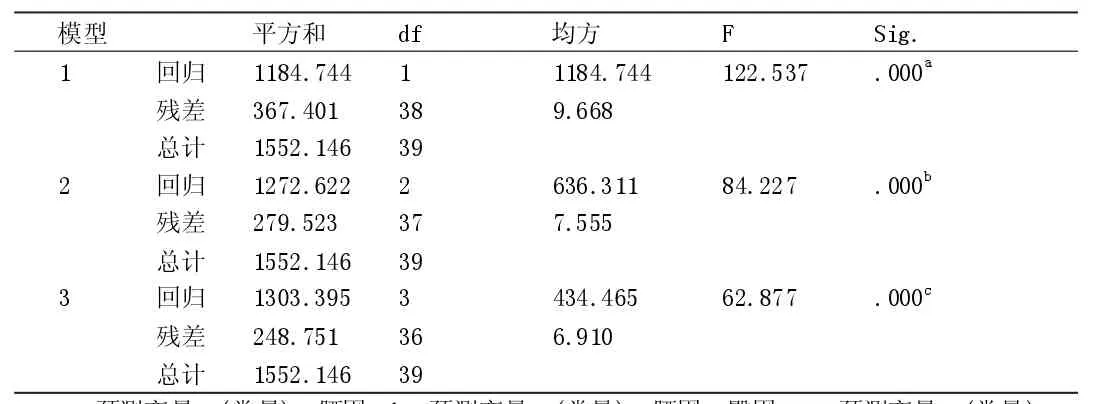
表7 逐步回归方差分析表(novad)
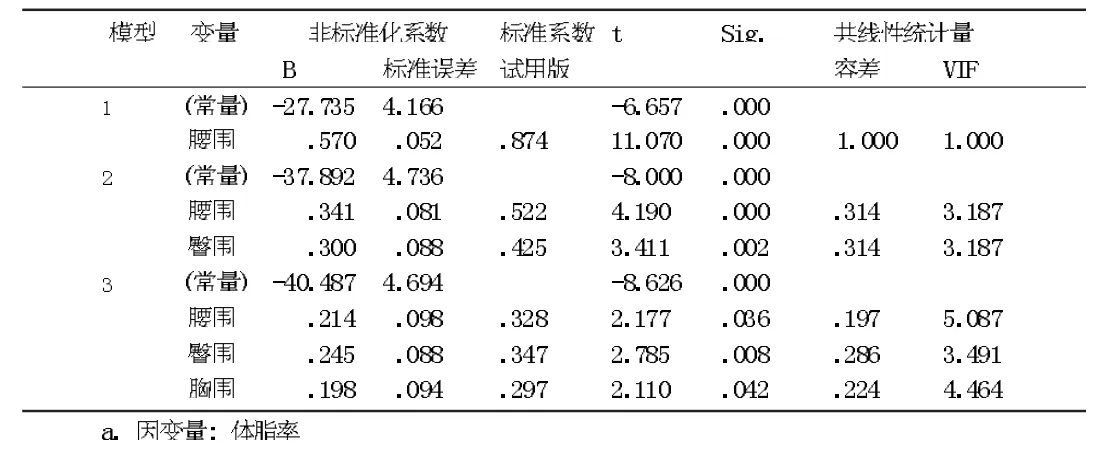
表8 逐步回归系数a分析表
由表9可以看出,模型3中第二维的条件指数大于15,第三维、第四维的条件指数均大于30,其特征值均接近于0,但在这三维中均未出现两个以上变量的方差比例同时大于50%的情况,因此不能认定存在共线性问题。这与表8的结论一致。
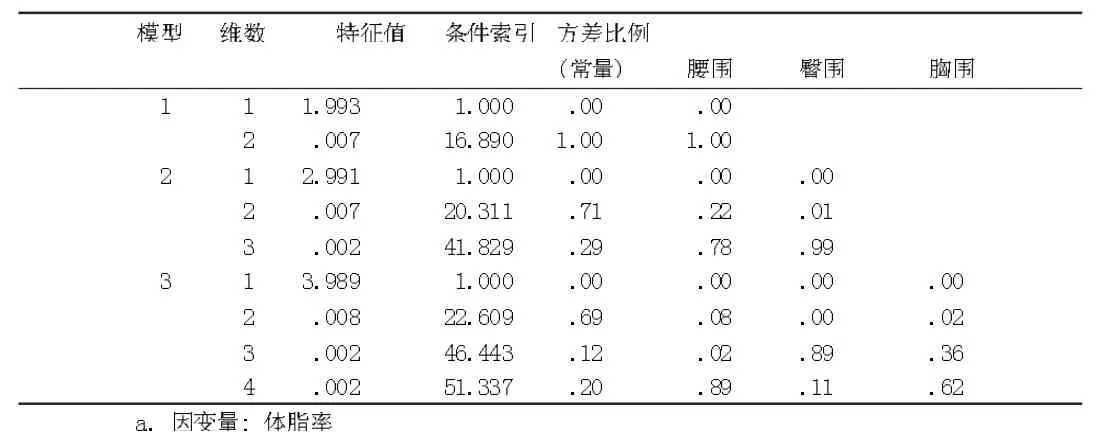
表9 逐步回归共线性诊断a分析表
5、结论
通过与全回归结果的对比分析,逐步回归的效果均优于全回归分析效果;影响体脂率的主要形态指标因素是胸围(x3)、腰围(x4)、臀围(x5)。
[1]权德庆主编.体育统计学[M].北京:人民体育出版社,2011.
[2]叶中行.概率论与数理统计[M].北京:北京大学出版社,2010.
[3]宇传华.SPSS统计分析[M].北京:电子工业出版社,2007.
[4]陈及治.体育统计[M].北京:人民体育出版社,2006.
[5]李世明.实用体育多元分析方法[M].北京:人民体育出版社, 2006.
G804
A
1006-8902-(2017)-08-SY
