基于粒子群优化的改进EMD算法在轴承故障特征提取中的应用

郭 泰， 邓忠民， 徐 萌

(1 北京航空航天大学 宇航学院，北京 100191；2 中国民航大学 电子信息与自动化学院，天津 300300)

基于粒子群优化的改进EMD算法在轴承故障特征提取中的应用

郭 泰1， 邓忠民1， 徐 萌2

(1 北京航空航天大学 宇航学院，北京 100191；2 中国民航大学 电子信息与自动化学院，天津 300300)

经验模态分解(Empirical Mode Decomposition, EMD)作为一种数据驱动的自适应信号分解方法，在轴承故障特征提取中有着广泛应用。针对EMD自身存在的模态混叠、端点效应以及三次样条插值带来的过冲/欠冲问题，同时考虑到有理Hermite插值方法具有一个形状控制参数，为选择最优的插值曲线提供了可能，基于此，提出了一种基于粒子群优化(Particle Swarm Optimization, PSO)的改进EMD算法，选定频率带宽作为IMF优劣评判准则，并以此作为PSO的评价函数；在筛分过程中，从众多不同形状控制参数对应的分解结果中寻找最优IMF从而确定最优形状控制参数；在每阶分解结果中都能保证所得IMF是最优的，从而达到更好的自适应性及更高精度。为验证所提出方法的有效性，采用传统EMD、EEMD与该算法对仿真信号进行处理、对比，并通过计算相关技术指标进行了验证。最优将其应用于滚动轴承故障特征提取，并与传统EMD算法、EEMD进行对比，包络谱结果显示，改进后的EMD算法具有更好的分解效果，抑制干扰并能提取出更多故障信息。

EMD；有理Hermite插值；PSO；轴承；故障特征提取

轴承作为旋转机械中运用最为广泛且关键的部件，众多故障皆来源于此[1]，同时，它的运行状态也直接影响了整台设备的产能以及精度。在实际运行环境下，轴承通常有以下几种故障形式：外圈故障、内圈故障、球故障以及几种复合情形。而这些故障原因多由于滑油污染、过载[2]、脉冲宽度调制逆变器电流泄露[3]等原因。为确保轴承运行的稳健，对于早期轴承故障状态进行识别是非常必要的。

与此同时，由于多数机械振动信号为非线性非平稳信号，传统意义下的傅里叶变换、Wigner-Vile分布(Wigner-Vile Distribution，WVD)、和小波变换(Wavelet Transform, WT)都存在其固有局限性，而不能成为完全自适应的信号分解方法。EMD作为一种数据驱动的时频处理方法，能够根据信号的局部特征时间尺度将一个复杂信号分解为若干固有模态函数(Intrinsic Mode Functions, IMF)之和。它是完全自适应的，因此非常适合于处理非线性非平稳振动信号。但EMD也存在其固有的缺陷如模态混叠、虚假模态及端点效应等。

因此，众多学者对基于EMD算法在轴承故障诊断中的应用进行了潜心研究。Yan等[4]通过将振动信号进行经验模态分解后得到瞬时频率幅值并用于滚动轴承故障特征提取；Rai等[5]通过对分解得到的IMF进行Fourier变换来提取各IMF频谱特征，从而提取故障频率;周浩等[6]提出一种基于EMD、峭度及Hilbert包络解调的轴承故障诊断方法；此后相关学者对EMD算法的改进尤其是插值方式进行了研究，Qin等[7]提出一种基于分段幂函数的包络算法并将其应用于Hilbert-Huang变换； Li等[8]在三次Hermite插值基础上提出了有理Hermite插值的方法。

本文在有理Hermite插值方法基础上，结合频率带宽准则、粒子群优化(PSO)提出一种基于优化思想的改进EMD算法，通过设定优劣评判准则，在每一阶分量获取过程中，根据不同形状控制参数所对应的不同上下包络，从预先得到的众多IMF中选择最优，从而确保在包络曲线合理的前提下，每一阶分解得到的IMF都是最优的，从而提升了整个算法的自适应性及分解效果。为验证算法的有效性，将所提出方法应用于仿真信号及轴承故障特征提取，并与传统EMD、EEMD进行对比，结果显示，本文提出的算法能够有效抑制模态混叠且具有更好的分解性能。

1 EMD算法概述

EMD算法能够将复杂的非线性非平稳信号自适应性地分解成为一系列不同特征尺度的固有模态函数(IMF)之和，其算法流程图如图1所示。

2 有理Hermite插值方法

有理Hermite插值方法是一种新提出的基于三次Hermite插值方法的带有形状控制参数的插值算法，因为其在插值过程中增加了一个形状控制参数，通过调整形状控制参数的大小可改变插值曲线的形状，因此为选取最优插值包络提供了可能并用于图1中上下包络的插值过程。

图1 传统EMD算法流程图Fig.1 Flow chart of thetraditional EMD algorithm

对于给定的离散序列 (xk,yk),k=1, 2, 3,…,N,yk是位于xk处的极大值或极小值，目的是要在区间(xk,xk+1),k=1, 2,…,N-1采用有理Hermite插值方法进行包络曲线拟合，假定hk=xk+1-xk为每个子区间长度，dk=P′(xk)为插值基函数在xk处的斜率，插值基函数的构造形式如下[9]

Fk(t)=1+(δ-3)t2-(2δ-2)t3+δt4

Fk+1(t)=-(δ-3)t2+(2δ-2)t3-δt4

Gk(t)=t+(δ-2)t2-(2δ-1)t3+δt4

Gk+1(t)=-(δ+1)t2+(2δ+1)t3-δt4

(1)

式中,t=(x-xk)/hk。

此外，以上基函数满足以式(2)关系

Fk(0)=Fk+1(1)=1,Fk(1)=Fk+1(0)=0

Gk(0)=Gk(1)=Gk+1(0)=Gk+1(1)=0

Fk(t)+Fk+1(t)=1,Gk(t)+Gk+1(1-t)=0

(2)

因此，插值基函数的最终表达式为

P(t)=yk+hkdkt+[-(δ-3)τkhk+(δ-2)hk×dk-(δ+1)hkdk+1]t2+[(2δ-2)τkhk-(2δ-1)hkdk+(2δ+1)hkdk+1]t3+[-δτkhk+δhkdk-δhkdk+1]t4

(3)

式中，τk=(yk+1-yk)/hk为差分系数。

插值基函数是一个关于t的四次多项式，因而结构明晰且计算方便。当δ=0时，该插值基函数退化为普通的三次Hermite插值，包络曲线的形状会随着δ值的改变而改变，同时这也意味着通过相关目标准则及优化算法可以获取最优的包络曲线。

3 基于粒子群优化(PSO)的改进EMD算法

本文基于PSO优化及有理Hermite插值方法提出一种改进EMD算法，该算法在EMD过程见(见图1)中采用Hermite插值代替传统三次样条插值，并根据频率带宽准则选取每阶最优的IMF(将此最优IMF定义为P-IMF，改进算法称为P-EMD)，从而能够确保算法更好的自适应性及更高的精度。

3.1 IMF优劣评判准则

通常IMF可近似为一个局部窄带信号，带宽越小意味着频率调制越小，因此带宽准则用来选择最优的IMF，带宽准则的详细信息阐述如下：

对于一个给定信号z(t)=a(t)ejΦ(t),信号在时间t的瞬时带宽为

(4)

瞬时带宽Bt用来形容信号z(t)的Wigner分布对中心瞬时频率的集中程度。当Bt非常小时，信号z(t)可认为是一个窄带信号。

信号z(t)的带宽B可分为以下两部分

(5)

3.2 基于PSO算法的改进EMD算法过程

基于PSO及有理Hermite插值方法的改进EMD算法，能够通过设定的IMF优劣准则在每阶分解过程中确定插值函数最优的形状控制参数，从而保证每阶IMF都是最优的。算法的主要步骤如图2所示。

其中，图2中形状控制参数寻优过程为整个算法过程的核心环节，其具体步骤如图3所示。

4 仿真验证

为验证算法的有效性并对相关性能分解指标进行对比，采用如下仿真信号x(t)[10]进行验证。x(t)=x1(t)+x2(t)，其中x1(t)=(1+0.5sin6πt)sin180πt，x2(t)=sin100πt，t=0 ∶1/1 000 ∶1。仿真信号x(t)及其组成分量信号在时域内的波形图如图4所示。

分别采用传统EMD、EEMD、P-EMD算法对仿真信号进行分解，分解结果分别如图5～图7所示。从图中可以看出，传统EMD算法在分解过程出现的模态混叠现象在EEMD、P-EMD结果中都得到有效抑制，但EEMD在抑制模态混叠的同时也引入了更多的虚假模态，而本文所提出的P-EMD改进算法不仅能够有效抑制模态混叠，且不引入虚假模态，具有更好的分解性能与重构性。

图2 改进EMD算法流程图Fig.2 Flow chart of theP-EMD algorithm

图3 形状控制参数寻优过程流程图Fig.3 Flow chart of shape controlling parameter optimization process

图4 信号x(t)及其分量的时域波形Fig.4 Waveform of the signal x(t) and its components

最后通过计算均方值误差RMSE、与真实分量的相关系数、正交指数三个指标对三种算法进行更直观的对比，结果显示在表1中。从表中可以看出，P-EMD改进算法在三种算法中，RMSE更接近于0，且相关系数更加趋于1，从而能够证明其分解结果精度更高，更接近真实值。此外正交指数最小，各分量具有最优的正交性。综合以上对比，P-EMD能够有效抑制传统EMD中出现的模态混叠，在三种算法中的分解结果中，P-EMD结果与真实分量具有最好的一致性。

图5 仿真信号x(t)传统EMD算法结果Fig.5 Traditional EMD decomposition results of simulation signal x(t)

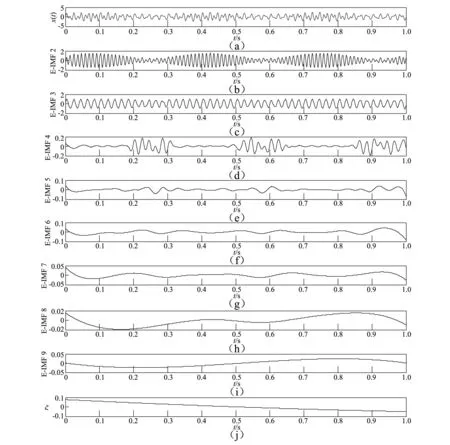
图6 仿真信号x(t)EEMD分解结果Fig.6 EEMD decomposition results of simulation signal x(t)

图7 仿真信号x(t)P-EMD算法分解结果Fig.7 P-EMD decomposition results of simulation signal x(t)

5 实验数据验证

本文提出一种新的基于PSO的改进EMD算法并有效应用于滚动轴承故障特征提取。首先，采用改进后EMD算法对带有故障的轴承振动信号进行分解，并取前5阶P-IMFs；其次，对每一阶P-IMF，采用经验AM-FM分解[11]获取瞬时幅值部分；最后，通过计算瞬时幅值的傅里叶变换求得每阶P-IMF对应的包络谱，根据包络谱可有效识别轴承故障，同时为验证所提方法在处理真实信号时的有效性，与传统EMD算法及EEMD进行对比，实验数据来自美国凯撒西储大学公开的轴承数据[12]。

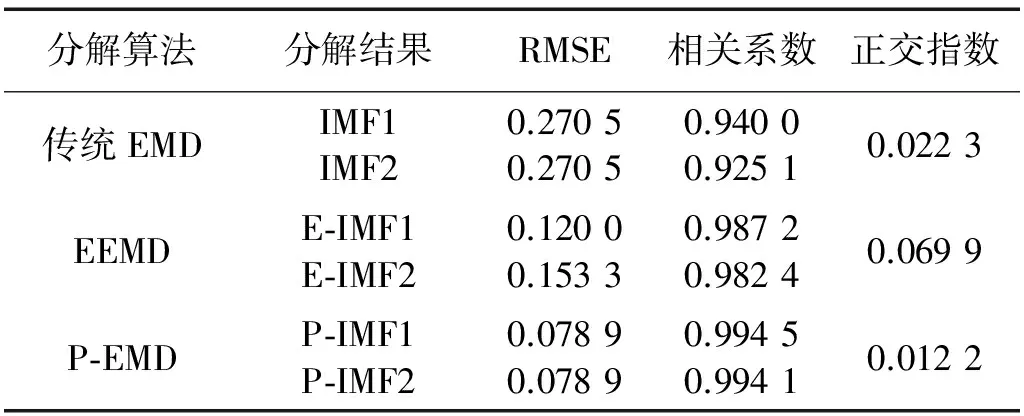
表1 三种算法分解性能指标对比

实验对象为6205-2RS JEM SKF型深沟球轴承，故障类型为单点故障，故障直径为0.177 8 mm，深度为0.279 4 mm，转速为1 797 r/min，在采样频率12 000 Hz下采集相应的振动加速度信号。文中分别以外圈、内圈为例，经计算转频为30 Hz，外圈故障频率f0为107 Hz，内圈故障频率fi为162 Hz。采集到的带有外圈、内圈故障的轴承振动信号分别如图8、图9所示。

图8 带有外圈故障的轴承振动信号时域波形Fig.8 The vibration signal waveform rolling bearing with outer fault

图9 带有内圈故障的轴承振动信号时域波形Fig.9 The vibration signal waveform of rolling bearing with inner fault

首先，分别采用传统EMD、EEMD与P-EMD算法对带有外圈故障的轴承振动信号进行分解，并取前5阶分量进行显示、对比与分析，分解结果分别如图10～图12所示。从各自分解结果的对比中可以看出，传统EMD分解结果中有较为明显的模态混叠现象，而EEMD与P-EMD则在每阶分量的时间特征尺度上更为均衡，模态混叠抑制效果明显。

图10 对带有外圈故障的轴承振动信号采用传统EMD算法的分解结果(IMFi(i=1,…,5)表示前5阶分量)Fig.10 The traditional EMD decomposition results of the vibration signal of bearing with outer ring fault(IMFi(i=1,…,5)stands for ith order component)

图11 对带有外圈故障的轴承振动信号采用EEMD算法的分解结果(E-IMFi(i=1,…,5)表示前5阶分量)Fig.11 The EEMD decomposition results of the vibration signal of the bearing with outer ring fault(E-IMFi(i=1,…,5)stands for ith order component)

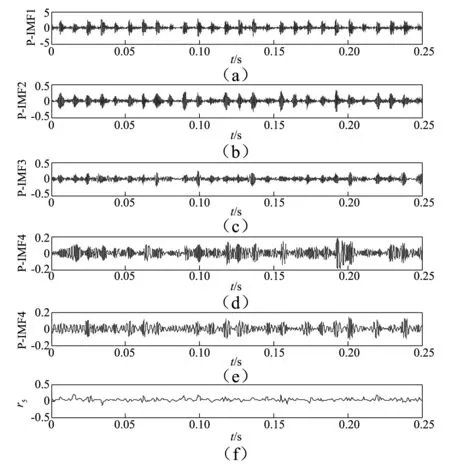
图12 对带有外圈故障的轴承振动信号采用P-EMD算法的分解结果(P-IMFi(i=1,…,5)表示前5阶分量)Fig.12 The P-EMD decomposition results of the vibration signal of the bearing with outer ring fault(P-IMFi(i=1,…,5) stands for ith order component)

对分解得到的各阶分量，采用经验AM-FM分解进行处理，得到各阶瞬时幅值分量，求得相对应包络谱，三种算法包络谱如图13所示。从图中可以看出，第3阶分量的包络谱都非常清晰，能够反映高频分量被故障频率调制的现象，但也可以看出EEMD信噪比在三幅谱图中较低；在第4阶IMF分量包络谱中有明显的干扰谱线，相反在E-IMF与P-IMF包络谱中得到很好的抑制，能够清晰判断故障频率；在第5阶IMF与E-IMF分量的包络谱中，已经不能提供有效的频率信息，而P-IMF包络谱仍能准确识别出故障频率。

同理，可以采用传统EMD算法、EEMD与P-EMD对带有内圈单点故障的轴承振动信号进行分解，其2、3、4阶分量对应的包络谱如图14所示。

根据图14中包络谱对比显示，第2阶分量的包络谱非常接近，相差不大；在第3阶IMF分量的包络谱中在132 Hz处有明显的干扰谱线，影响对故障频率的判断，但在对应E-IMF与P-IMF包络谱中干扰谱线得到抑制，谱线较为清晰，但E-IMF包络谱信噪比略低于P-IMF；第4阶IMF分量包络谱不能提供有效信息，E-IMF虽能够提供二倍转频，但谱线已不太明显，而相应P-IMF包络谱仍能提供清晰的2倍轴频与故障频率谱线。因此，比较而言，所提出的P-EMD算法相对传统EMD算法与EEMD算法有一定优越性，在抑制模态混叠的同时具有更好的分解性能。

图13 IMFi、E-IMFi与P-IMFi(i=3,4,5)的包络谱Fig.13 Envelope spectra of IMFi、E-IMFi and P-IMFi(i=3,4,5)

图14 IMFi、E-IMFi与P-IMFi(i=2,3,4)的包络谱Fig.14 Envelope spectra of IMFi, E-IMFi and P-IMFi(i=2,3,4)

6 结 论

本文结合有理Hermite插值方法与带宽选取准则及PSO提出一种改进型EMD算法，并对基于EMD与包络谱相结合用于滚动轴承故障特征提取的相关理论进行了介绍，通过对仿真信号的结果对比与故障轴承实验数据的处理，能够得出以下结论：

所提出的改进型EMD算法是一种较为优秀的信号分解方法，能够避免传统EMD分解过程中出现的模态混叠现象，提升分解精度与性能。

结合经验AM-FM分解求取包络谱，所提出方法能够有效应用于带有外圈、内圈单点故障的滚动轴承特征提取。

相比于传统EMD算法，所提出的改进EMD方法能够有效抑制干扰谱线，为进一步故障分类等处理提供更多、更准确信息，且与EEMD相比，具有更高信噪比。

综上，将有理Hermite插值方法与PSO结合的改进型EMD算法是一种有效的信号分解方法。当然，目前该方法仍有不成熟的地方，比如算法耗时较长，关于IMF优劣的判别准则仍需要继续研究，但相信基于优化思想的改进型EMD算法能够为信号分解提供一种新的思路。

[ 1 ] ALI J B, FNAIECH N, SAIDI L, et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals[J]. Applied Acoustics, 2015, 89(2):16-27.

[ 2 ] DYBALA J, ZIMROZ R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal[J]. Applied Acoustics, 2014, 77(3):195-203.

[ 3 ] SOUALHI A, MEDJAHER K, ZERHOUNI N. Bearing health monitoring based on Hilbert-Huang transform, support vector machine, and regression[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(1):52 - 62.

[ 4 ] YAN R, GAO R X. Hilbert-Huang transform-based vibration signal analysis for machine health monitoring[J]. IEEE Transactions on Instrumentation & Measurement, 2006, 55(6):2320-2329.

[ 5 ] RAI V K, MOHANTY A R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform[J]. Mechanical Systems & Signal Processing, 2007, 21(6):2607-2615.

[ 6 ] 周浩, 贾民平. 基于EMD和峭度的Hilbert包络解调在滚动轴承故障诊断中的应用分析[J]. 机电工程, 2014, 31(9):1136-1139. ZHOU Hao, JIA Minping. Analysis of rolling bearing fault diagnosis based on EMD and kurtosis Hilbert envelope demodulation [J]. Journal of Mechanical & Electrical Engineering, 2014, 31(9):1136-1139.

[ 7 ] QIN S R, ZHONG Y M. A new envelope algorithm of Hilbert-Huang Transform[J]. Mechanical Systems & Signal Processing, 2006, 20(8):1941-1952.

[ 8 ] LI Y, XU M, WEI Y, et al. An improvement EMD method based on the optimized rational Hermite interpolation approach and its application to gear fault diagnosis[J]. Measurement, 2015, 63:330-345.

[ 9 ] 郑近德, 程军圣, 曾鸣, 等. 广义经验模态分解性能分析与应用 [J]. 振动与冲击, 2015, 34(3): 123-128. ZHENG Jinde, CHENG Junsheng, ZENG Ming, et al. Performance analysis and application of generalized empirical mode decomposition [J]. Journal of Vibration and Shock, 2015, 34(3): 123-128.

[10] ZHENG J, CHENG J, YANG Y. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems & Signal Processing, 2013, 40(1):136-153.

[11] WU Z, HUANG N E, LONG S R, et al. On instantaneous frequency [J]. Advances in Adaptive Data Analysis，2009, 1(2): 177-229.

[12] Case Western Reserve Univesity. Bearing Data [EB/OL]. http:∥csegroups.case.edu/bearingdatacenter/pages/download-data-file.

An improved EMD algorithm based on particle swarm optimization and its application to fault feature extraction of bearings

GUO Tai1, DENG Zhongmin1, XU Meng2

(1. School of Astronautics, Beihang University, Beijing 100191, China; 2. School of Electronic Information and Automation, Civil Aviation University of China, Tianjin 300300, China)

Empirical mode decomposition (EMD), as a data driven and adaptive signal decomposition method, was widely utilized in fault feature extraction of bearings. This work aims to solve the problems of mode mixing, end effect and the overshoot or undershoot brought by cubic spline interpolation. Meanwhile, the rational Hermite interpolation method has a shape controlling parameter, which can change the shape of interpolation curve, was considered. An improved EMD algorithm based on particle swarm optimization (PSO) and rational Hermite interpolation was put forward. Firstly, the frequency bandwidth, as the evaluation function of PSO, was used to select optimal IMF. Secondly, the optimal IMF from many different decomposition results was found out and the optimal shape controlling parameters were determined. Finally, the obtained IMF was optimal in each step of the decomposition result. Therefore, better adaptability and higher accuracy could be achieved. To verify the effectiveness of the presented method, a simulation signal was processed by traditional EMD, EEMD and improved EMD, respectively. The comparison results show that the introduced algorithm can effectively restrain the mode mixing and the obtained IMF has better consistency with the real component. Eventually, the improved EMD was applied to fault feature extraction of rolling bearings and compared with the traditional EMD, EEMD. The envelope spectra indicate that the proposed algorithm has better decomposability, ability of restraining interference and can extract more fault information.

empirical mode decomposition(EMD); rational Hermite interpolation;particle swarm optimization(PSO); bearing; fault feature extraction

国家自然科学基金(10972019)

2016-03-08 修改稿收到日期： 2016-06-29

郭泰 男，硕士生，1992年生

邓忠民 男，博士,教授，1968年生

TH165；TN911

A

10.13465/j.cnki.jvs.2017.16.028