基于改进EEMD样本熵的高速列车滚子缺陷AE信号提取

邓 韬， 林建辉， 黄晨光， 靳 行， 张 敏

(西南交通大学 牵引动力国家重点实验室，成都 610031)

基于改进EEMD样本熵的高速列车滚子缺陷AE信号提取

邓 韬， 林建辉， 黄晨光， 靳 行， 张 敏

(西南交通大学 牵引动力国家重点实验室，成都 610031)

提出一种改进EEMD滚子缺陷声发射(AE)信号提取新方法，该方法根据EMD分解的二进滤波器组特性构造幅值与频率成线性-正弦规律变化的噪声添加进测试数据，给出了噪声构建原则，并按频率由高到低限定各阶IMF筛选次数，选取同一时段高频IMF归一化样本熵较小的数据段作为声发射事件参考。对实测数据计算表明特殊构造的噪声和筛选次数能有效抑制中低频段模态混叠和高阶IMF小波消失现象，改进后的EEMD方法分解出的IMF分量物理意义明确，性能优于传统EEMD方法。分段的IMF样本熵变化能在连续监测中捕捉声发射事件，对应的Hilbert谱能直观凸显出滚子缺陷声发射信号，滚动体AE信号事件周期与理论计算相吻合。

声发射； 改进EEMD； 分段样本熵； 滚子缺陷

高速列车轮轴故障检测的重点在于其早期故障的发现和预警[1]，声发射(Acoustic Emission，AE)检测作为一种早期故障检测手段其信号比振动加速度频率范围宽、包含的信息量大、受外界干扰情况更复杂，对轮轴AE信号的有效捕捉分析一直是研究的难点。

经验模式分解(Empirical Mode Decomposition，EMD)作为依据数据自身驱动的分析方法[2-3]使声发射这种非高斯、非线性信号有了全新的分析手段。针对EMD算法和待分解信号频率特征影响易产生模态混叠的现象，由Wu等[4]提出的聚合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)通过加入噪声辅助分析(Noise-Assisted Data Analysis，NADA)改变信号极值点分布，多次平均后在一定程度上减轻了信号由间断点带来的模态混叠，该方法得到了较好的运用[5-7]。然而其添加噪声的幅值和筛选次数对EEMD最终分解结果影响很大。其次，噪声幅值和筛选次数都是人为根据经验设定，最终结果受主观因素影响很大。基于此，雷亚国等[8]提出一种自适应总体平均经验模式分解用于行星齿轮箱故障检测，该方法对振动信号加入幅值随频率呈正弦变化的噪声，每阶本征模态分量(Intrinsic Mode Function，IMF)都自适应地选择不同的筛选次数，克服了上述EEMD 方法对所有 IMF用人为设定的等幅值噪声和相同筛选次数问题。

本文提出一种MEEMD(Modifled Ensemble Empirical Mode Decomposition)方法，即根据高速列车轴承钢质滚动体、保持架的声发射信号特征，结合EEMD二进滤波特性，在EEMD中设计加入一种呈线性-正弦规律变化的噪声。选取最可能包含声发射特征频段的前几个低阶IMF分别进行分段样本熵计算，同一时刻不同尺度下样本熵都明显较小的几个数据段信号随机性较小，有较大概率是声发射信号，对其进行希尔伯特变换，可进一步研究其谱分布。该方法可减小声发射信号的模态混叠现象，能够在复杂测试环境下对含有高噪声的大段连续轮轴监测数据进行声发射信号的捕捉和观察。

1 AE信号的EEMD改进方法

1.1 EEMD算法及噪声加入原则

EMD算法先要寻找到信号的局部极值点，再由三次样条曲线分别连接这些局部极大值和极小值点得到上下包络线，继而求出信号的均值曲线。通过EMD的二进滤波器组特性对高斯白噪声进行研究发现[9]，不同阶次的IMF频带范围是不同的，低阶IMF分量属于高频分量，包含有相对较宽的频率成分，高阶IMF分量属于低频分量，频率成分相对较少。因此，众多的高频成分会集中出现在同一个低阶IMF中，而单一的低频成分则可能会分散在多个高阶IMF中。

如果信号中包含有异常点如间断点等，极值点的选取会因此而发生改变，信号经上下包络求取均值最后得到IMF分量一连串受到影响，在同一IMF中最终包含有原有信号和异常信号的“多重”模态，从而产生了模态混叠。

为了解决EMD存在的模态混叠现象，由Wu等提出了基于噪声辅助分析(NADA)的EEMD方法。其基本思路是对原信号加入高斯白噪声，因高斯白噪声谱分布均匀，它的加入如同在各个时间尺度下画好“格子”，不同时间尺度的信号会填入这个格子中间。同时噪声的加入一定程度上能弱化异常信号的影响。根据高斯白噪声具有的零均值性，EEMD多次平均后能把每次加入的噪声基本抵消，噪声对最终分解结果影响很小。

EEMD算法如下：

(1)设定聚合的总次数N,加入高斯白噪声的幅值比值系数k，令计算次数a=1。其中k为加入的白噪声幅值标准差en与原始信号幅值标准差e0的比值系数。

(2)计算第a次时，在信号中加入高斯白噪声na(t)后的实验信号，即

Xa(t)=x(t)+kna(t)

(1)

(3)对Xa(t)进行经验模式分解共得到I个模态分量，即IMFci,a(i=0,1,…,I)，其中ci,a为第i次分解得到的第a个IMF；

(4)计算所有a次聚合后对应IMF的均值

(2)

(5)把各个IMF的均值作为信号最终的IMF输出。

Wu等[10]研究了在聚合经验模态分解中添加白噪声的幅值比值系数和聚合次数设定之间的关系,文中给出了噪声对分解结果影响e与N，K有

(3)

式中：N为聚合次数;k为噪声幅值比值系数;e为信号分解相对误差的期望最小值,代表原信号与EEMD分解后IMFs的相对误差。

实际使用可以发现EEMD是通过在全频段添加相同强度的白噪声来实现对信号极值点“修正”的，只能在一定程度上削弱单纯EMD的模式混叠现象，根据具体信号的不同，模式混叠现象还有可能发生。雷亚国等对一包含冲击、高频余弦和低频余弦的仿真信号进行EEMD分解，分别设定添加的噪声标准差为原始信号标准差的 0.001 倍和0.01 倍时可以发现，加入较小噪声时高频出现了模式混叠，加入较大噪声时低频出现了模式混叠，基于此提出了按正弦规律变化的噪声加入方法。总结而言，EEMD产生模式混叠的原因与分解过程中高频成分与低频成分对加入噪声大小的敏感性不同相关。

1.2 改进的噪声加入方法

有别于一般的振动加速度信号，声发射信号往往是一种突发的宽频信号，金属材料出现裂纹等缺陷时往往在某些特定频段或频率范围表现出较高能量，表1给出了一般钢材处于静态加载条件下，分别在韧性撕裂、孔洞和夹杂物起裂分离和准解理脆断三种情况下的声发射信号强度和频率特性。轮轴缺陷声发射信号所涉及的频段根据不同的缺陷主频涵盖从90～350 kHZ的频段，并且频域可从300 kHz延伸到1 MHz以上，分析此类信号不仅需要关注较宽的主频段还要兼顾延伸出去的超高频段，这一超高频段包含有缺陷轮轴声发射信号所具有的特征成分。

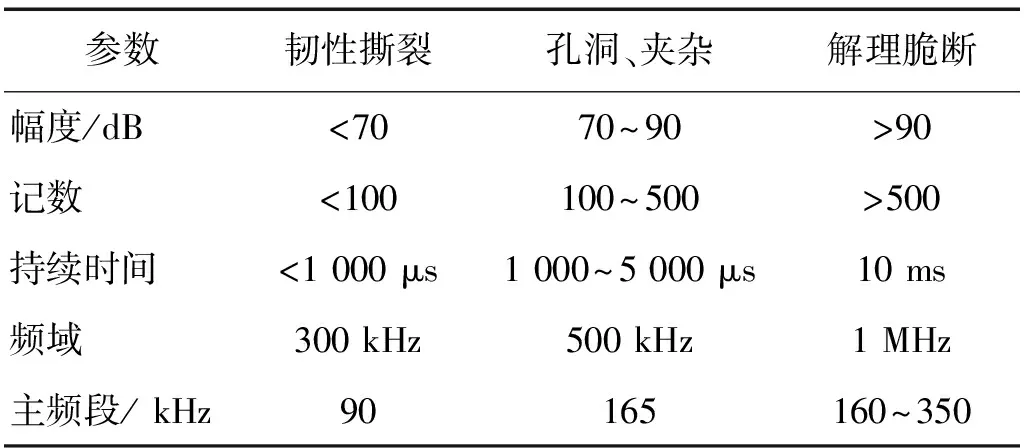
表1 一般钢材几种缺陷的信号特征

当信号中添加较小幅值噪声时，对低频成分极值点影响轻微，可减少低频成分被分散到多个 IMF 中的几率；信号中添加较大幅值噪声时，噪声所刻画的“尺度”更明晰，利于高频分量分解到对应的频率框架中，减轻高频成分的模态混叠现象。

按信号频率由低到高研究幅值以线性递增和正弦递增的两种噪声，发现在低频段加入幅值按线性规律递增的噪声，在高频段加入幅值按正弦规律递增的噪声更能契合声发射信号频段构成，有较理想的分解结果。为使中低频噪声加入可控，引入由低到高成线性-正弦变化的噪声频谱构成为

(4)

式中：F(f)为高斯白噪声频谱；F0(f)为线性-正弦噪声频谱；f0为1/2采样率；引入τ为线性和正弦噪声节点算子。

图1为不同τ下的线性-正弦噪声频谱图，采用归一化的噪声频率幅值描述。拟合的线性-正弦噪声相比单纯的线性变化噪声在高频段幅值递增更平滑，在低频段噪声衰减更直接。引入的τ与线性变化区和正弦变化区分割点相关，改变τ的取值可以改变线性区和正弦区的比例。τ值越大线性区越小，正弦区越大，低频中频率较高的部分更多的被正弦区覆盖，加入的噪声较多；τ值越小线性区越大，正弦区越小，当从最低频到较高频都处于线性段时，有较陡峭的噪声幅值变化，加入噪声相比正弦变化要更小。对一个完整的声发射信号，通过调整τ使得最低特征频率段以下的部分处于线性变化段使噪声加入量变小，利于后期分解。

图1 不同τ下的线性-正弦噪声频谱图Fig.1 Linear-sinusoidal noise spectrum in different τ

1.3 IMF筛选次数优化

根据EEMD 的二进滤波器特性可知，最高频率IMF即一阶IMF包含的频带宽度是最宽的，从一阶依次往下各阶IMF包含频宽基本呈现2 的指数次衰减；此外，各阶IMF所包含的频带重叠情况不一，越往高频带重叠情况越大。所以，对不同阶次的IMF应当设定不同的筛选次数，由大量仿真数据可知，对于最高阶即最低频IMF分量，只需进行2次筛选就能得到稳定的结果，对于每低一阶的IMF分量筛选次数增加的足够大才能有效的减小模态混叠现象。

因此，根据分解后各IMF分量的复杂度，参考类比 EEMD所具有的二进滤波器特性，第一阶IMF分量所含频率成分最多，需要的聚合次数也最高，其他IMF所需聚合次数依次降低。于是考虑按频率由高到低以2的指数次方衰减规律变化确定筛选次数，IMF阶次由低到高设定聚合次数N为2n，2n-1，…，2；其中n为IMF分量个数。

2 IMF样本熵筛选和谱分析

2.1 本征模态函数样本熵

样本熵(SampEn)是一种测量信号复杂度或不规则度的指标，取值越大，不规则度越大。

声发射信号是突发冲击信号，对每一阶IMF分量分别计算其样本熵，包含此类高频冲击信号的IMF小波形很多，样本熵值较高；包含由转动频率带来的各阶调制频率成分的高阶IMF幅值突变小，较为连续且规律，属于中大波形，能量较大，其样本熵值往往偏小，剔除那些样本熵值较小的IMF分量可以避免较大能量在频率图谱上盖过能量较小的声发射信号，凸显其谱线。

作为近似熵的改进算法，样本熵不再计算自身匹配,而是从计算样本产生信息量比率入手。样本熵在计算条件概率时也不再采用模板匹配方式,计算中只需设定一个长度为m的模板向量，然后通过寻找m+1长度匹配的方式来得到熵值，因而不再需要长度为m+1的模板向量。样本熵能够克服近似熵的计算偏差，且速度更快，具有更高精度。

一个时间序列样本熵的计算如下[11]。

对于一个数据量为D的时间序列{x(i):j=1,2,…,D}，可以构成D-m+1个相空间矢量Xm(i)，有{i│1≤i≤D-m+1},Xm(i)={u(i+k):0≤K≤m-1}为u(i)～u(i+m-1)的m个相空间向量。

定义两个m维的矢量X(i)与X(j)之间的最大距离为

k=0,1,…,m-1

(5)

(6)

同样的对m+1可以得到Bm+1(r)，用平均值表示，序列的样本熵定义为

(7)

对于数据长度为有限D的时间序列样本熵估计值为

(8)

数据经EEMD后获得的n个IMF分别按一定数据长度计算其样本熵得到{Se(I):I=1,2,…,n}，I为IMF阶次数，于是有归一化样本熵

(9)

定义归一化样本熵指标

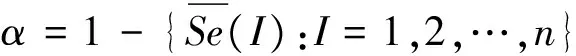
(10)

前γ个高频段IMF分段归一化样本熵值相加有

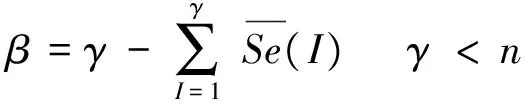
(11)

由式(11)可知α<1,β<γ，其中α主要表征单个低阶高频的IMF样本熵大小，而β对应相应数据段下的前γ个高频IMF分量所包含的信号变化剧烈程度，α和β越大，说明随机噪声可能性越小，为声发射事件的概率也越大。α、β作为较高频率IMF信号随机性判据必须同时满足不小于某一值，其大小可根据具体数据和高频IMF分量的个数γ作调整。

2.2 Hilbert谱分析

Hilbert谱是通过对各IMF分量进行Hilbert变换得到相应时频幅值谱图的谱分析方法[12]，有

(12)

由式(12)可以看出Hilbert谱给出的是频率、幅值和时间的三维关系谱图。EMD分解把复杂的信号分界为简单的单分量的信号，使其可以应用瞬时频率的概念，Hilbert变换的目的就是分析出瞬时频率。

对比Gabor、小波等具有多尺度的时频分析方法，得到的是一个包含时频分布的二维矩阵。所以HHT在每一时刻只计算出一个频率值，而小波等得到的是一系列的频率值。从Hilbert谱时频分布图上看到的是一条线，而不是一幅图，这一特点更利于观测到短时突发特征的AE信号。

图2给出了整个改进EEMD的样本熵计算Hilbert谱的步骤。

图2 改进EEMD分段样本熵绘制信号Hilbert谱Fig.2 AE Hilbertspectrumbased onmodified EEMD and segmentsample entropy

3 实验设计与数据分析

3.1 试验布置

高速列车双列圆锥滚子轴承主要由滚动体、内滚道、外滚道和保持架等构成。滚动体缺陷为沿其纵向烧蚀的一条凹痕，深度1 mm，宽度1 mm，两个故障滚动体间隔4个正常滚动体。

转动试验台如图3所示，设备主要由底部的电机驱动轮和上部的液压加压固定装置构成。声发射传感器用钢板螺丝夹具固定于轴箱侧面，每侧2个传感器，上下放置。实验设置采样率1 Msps，带宽20～400 kHz，触发门限60 dB，放大器放大倍率20 dB。

图3 试验台Fig.3 Experimental platform

3.2 数据分析

不同于静态检测时的门限触发采样，试验采用连续波形流采样以获得时间和波形连续的测试数据。图4为试验速度100 km/h工况下连续波形采样获得的数据时域图(横坐标为数据点数)。

图4 试验数据时域图Fig.4 Test signals

对测试数据进行EEMD分解，设定加入的高斯白噪声幅值系数为0.2，聚合次数200次，共得到9个IMF分量。图5(a)是分解后前5个IMF，从图中可以看到最高频率的IMF1分量只有幅值变化很小的连续小波形；IMF2分量只在8 400点处分解出较大波动；对应图5(a)方框中数据，观察IMF3的分解结果中4 080点、6 200点、8 200点、10 300点和15 400点的波形有较大可能为声发射事件，但这一宽频事件并没有在较高频率的IMF1和IMF2中体现出来，分解结果难以判定声发射事件。

图5 EEMD分解结果Fig.5 IMFs by EEMD

之前EEMD分解了解到IMF1分量的中心频率在350 kHz，为了确定改进噪声添加中的τ值，以350 kHz为中心频率、上下浮动10 kHz拟合一段长度为2 000点的窄带声发射信号如图6所示。图6下部时域信号为相同环境下声发射传感器采集到的一段正常轴承运行波型，每隔15 000点截取5组40 000点长度的数据(数据1～数据5)，分别做FFT获得各组数据350 kHz上下10 kHz频段范围的平均幅值。

图6 仿真信号Fig.6 Simulation signals

为了适当凸显声发射事件，分别将拟合声发射信号按各组得到平均幅值的5倍大小处理后叠加。对添加了拟合声发射信号的5段数据按τ值取20、6、1.5、1做噪声改进EEMD分解。对包含中心频率350 kHz最丰富的IMF1分量按拟合信号叠加起止点截取2 000点数据。表2为各IMF分量截取数据与原始窄带声发射信号的相关情况，可以看到当τ值为1.5时，即正弦噪声和线性噪声结合点在330 kHz时分解出各组数据和原始拟合信号的相关程度最高，因此τ值选取应尽量使线性-正弦结合点在所关心频率附近。

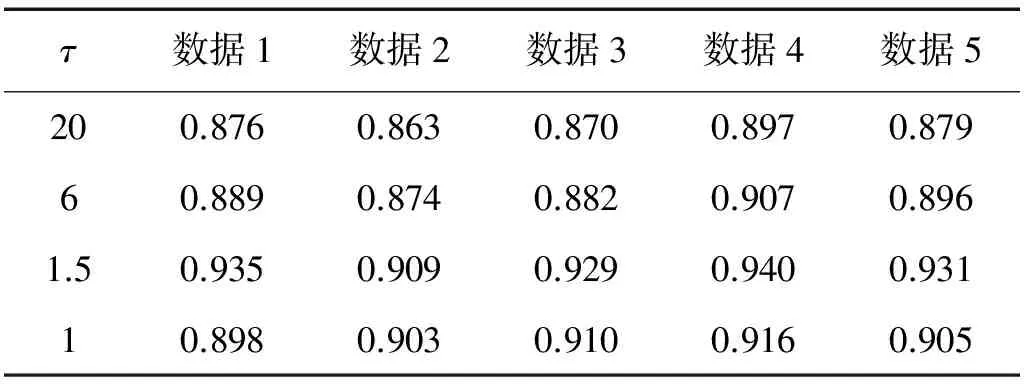
表2 不同τ值下各组分解结果相关性比较

对测得的包含滚动体缺陷连续波形数据采用改进后的EEMD方法进行分解，IMF2分量中心频率在225 kHz，结合前段分析，考虑对IMF2中心频率以下的加入噪声进行线性添加取τ值为2.5，最高白噪声幅值系数比取0.2做线性-正弦噪声计算得到新的噪声进行EEMD，聚合次数按照29，28，…，2计算得到前7个IMF分量如图7所示。

图7 改进后的EEMD分解结果Fig.7 IMFs by modified EEMD

图7(b)和图7(c)为图7(a)中方框部分放大结果，可以看到在同一时刻前三个分量有明显尖峰信号出现，符合声发射同一时刻有较宽频率脉冲波发出的情况，物理意义明确。显然传统的EEMD把前两个分量的小脉冲分解到了IMF3中，产生模态混叠。

为了在较长的监测数据中提取有效声发射信号，对每个IMF按数据长度N为5 000点分段进行三组样本熵计算。嵌入维数m是截取数据长度，一般m取1或2，实际应该优先选2，因基于联合概率重构可得到更多的详细信息。当m>2时数据长度太大，难以保证所截取信号具有相同的性质；且m>2时相应的r值也加大，计算的样本熵会难以反映序列的详细信息，因此，取m=2。

相似容限r为各模式间的有效阈值，是维数为m的超立方体半径。Pincus[13]对确定性过程和随机过程进行分析，认为r值过小对统计概率估计不理想，过大又会丢失较多的细节信息，得出r在0.1E～0.25E可以估计出较为有效的统计特性(E是原始数据的标准偏差，这里为各阶IMF的标准差)。因此，选取r=0.2E。

计算得到前7个IMF 4组分段样本熵判据变化结果如图8所示，α，β越大说明样本熵越小，而随机噪声样本熵一般较大。γ=3，通过多组的对比取α最低界限为0.1，β为0.59，图7(b)和图7(c)前三个IMF满足α，β分别为0.76和1.15均大于设定的最小值，于是判定5 00点～15 000点为包含声发射事件数据段。

图8 4组分段的前7个IMF归一化样本熵指标Fig.8 Segmentsample entropy of the first seven IMFs

图9给出了前10万点数据用前三个较小样本熵IMF计算的Hilbert谱。通过对比可以清晰的看到在5 000点～20 000点间有几组频宽在250 kHz和350 kHz的谱线，这种在同一时间点出现的几个连续宽频能量谱线明显区别于随机噪声，具有典型的声发射频谱特征。

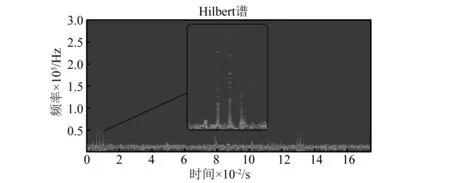
图9 Hilbert谱Fig.9 The Hilbert spectrum

通过对200 km/h速度下连续采集的信号进行分析，设定声发射事件闭锁时间为100 ms，可以得到4组独立的每隔0.014 7 s的声发射事件脉冲。双列圆锥滚子轴承滚动体故障特征频率计算公式为

(13)

式中：d为滚动体直径，mm；D为轴承直径(内圈和外圈直径的平均值)，mm；α为压力角(接触角)。通过计算可得200 km/h速度下单个滚动体缺陷触发频率为68 Hz，这与0.014 7 s的声发射事件脉冲数是吻合的。

4 结 论

本文针对高速列车轮轴缺陷声发射检测，提出了一种基于添加线性-正弦噪声和依据频率限定聚合次数的EEMD新方法，给出了拟合改进添加噪声曲线的初步经验。相比于改进前，该方法能更有效的契合声发射信号频率分布和能量分布，较好的避免模态混叠。对包含声发射事件的数据，其分解结果物理意义明确。通过分段计算IMF样本熵，建立了高频IMF分段样本熵与声发射事件的对应判定关系，在长时间连续采样数据段中判定并筛选出声发射事件，对应的Hilbert谱观察到连续的宽频谱线进一步验证了该方法的有效性，实测数据的滚动体缺陷与理论计算情况吻合度高，取得了不错的结果。

[ 1 ] 刘方,沈长青，何清波，等.基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究[J] . 振动与冲击,2013, 32 (24): 104-109. LIU Fang, SHEN Changqing，HE Qingbo,et al. Wayside acoustic fault diagnosis for locomotive bearings based on doppler effect correction and EEMD method in time domain [J]. Journal of Vibration and Shock, 2013, 32 (24): 104-109.

[ 2 ] WANG K S, HEYNS P S. Application of computed order tracking,Vold Kalman filtering and EMD in rotating machine vibration [J]. Mechanical Systems and Signal Processing, 2011, 25(1): 416-430.

[ 3 ] YUNLONG Z, PENG Z. Vibration fault diagnosis method of centrifugal pump based on EMD complexity feature and least square support vector machine [J]. Energy Procedia, 2012, 17: 939-945.

[ 4 ] WU Z H,HUANG N E. Ensemble empirical mode decomposition:a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009,1(1):1-41.

[ 5 ] 沈长青,谢伟达，朱忠奎，等.基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J].振动与冲击,2013,32(2): 39-43. SHEN Changqing, XIE Weida, ZHU Zhongkui,et al. Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method [J]. Journal of Vibration and Shock, 2013,32(2): 76-80.

[ 6 ] LEI Y, HE Z Y.Application of the EEMD method to rotorfault diagnosis of rotating machinery [J].Mechanical Systems and Signal Processing,2009,23(4):1327-1338.

[ 7 ] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012，32(11): 106-111. HU Aijun, MA Wanli, TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J].Proceedings of the CSEE, 2012,32(11): 106-111.

[ 8 ] 雷亚国, 孔德同, 李乃鹏，等.自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报， 2014，50(3)：64-70. LEI Yaguo, KONG Detong, LI Naipeng, et al.Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering, 2014，50(3)：64-70.

[ 9 ] FLANDRIN P，GABRIEL R，PAULO G. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letter，2004,11(2):112-114.

[10] WU Zhaohua, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J].Proceedings of the Royal Society, 2004, 454: 1597-1611.

[11] RICHMANM J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy [J]. American Journal of Physiology Heart & Circulatory Physiology, 2000, 278(6):2039.

[12] 陈双喜,林建辉,陈建政.基于希尔伯特-黄变换提取车桥耦合系统时频特性[J].振动与冲击,2012, 31(15): 175-179. CHEN Shuangxi, LIN Jianhui. Time-frequency characteristics extraction for vehicle/bridgecoupled system based on Hilbert-Huang transformation [J]. Journal of Vibration and Shock,2012, 31(15): 175-179.

[13] PINCUS S M．Approximate entropy as a measure of system complexity[J]. Proc. Natl. Acad. Sci. USA, 1991, 88:2297-2301.

AE signal extraction of a high speed train roller based on modified EEMD and segment sample entropy

DENG Tao, LIN Jianhui, HUANG Chenguang, JIN Hang, ZHANG Min

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

A new method of high speed train roller AE signal extraction was presented. The EMD acted as a dyadic filter bank and noise with proportional amplitude and frequency was added to the tested data. The sifting number was set by frequencies from high to low. Then, IMF’s segment sample entropy was calculated along the timeline, which took a larger proportion and was identified as an AE event. The experimental result shows that the Linear-Sinusoidal noise spectrum and sifting number could restrain the mode mixing and the little wave vanishing. The modified EEMD obtained a tangible physical meaning and improved results compared with the original EEMD. Segment sample entropy could capture the AE events in a continuous monitoring data. The AE signal was intuitively reflect in the corresponding Hilbert spectrogram. The roller AE signals were consistent with the theoretical calculation.

acoustic emission; modifled ensemble empirical mode decomposition(MEEMD); segment sample entropy; roller defect

国家自然科学基金重点项目(61134002)

2016-06-06 修改稿收到日期： 2016-06-27

邓韬 男,博士生,1987年9月生

林建辉 男,博士,教授,博士生导师,1964年10月生

TN911.7；TH17

A

10.13465/j.cnki.jvs.2017.16.023