基于奇异值分解的液压信号时域分解方法
2017-08-31张小明张梅军
张小明,唐 建,张梅军
(中国人民解放军理工大学 野战工程学院,南京 210007)
基于奇异值分解的液压信号时域分解方法
张小明,唐 建,张梅军
(中国人民解放军理工大学 野战工程学院,南京 210007)
为了抑制模态混叠和降低分量中的噪声含量,提出了一种基于奇异值分解的液压信号时域分解方法。根据奇异值分解的两点特性:①每个频率成分对应两个大小相当的奇异值;②各频率对应的奇异值的大小与该频率的振幅呈正相关,该方法先选取原信号中的某一频率,向其中叠加频率相同、振幅已知的周期信号,使叠加信号中该频率的振幅最大,这样与其对应的奇异值一定位于对角矩阵的前两阶,解决了原信号该频率的奇异值阶数无法确定的问题,继而选取前两阶奇异值重构,再减去前步加入的周期信号,即还原出原信号中该频率的时间序列。同样,对于原信号中的其他频率用相同方法处理,最终获得一组分量。经实验,该方法较EMD不仅能有效消除模态混叠,而且降低了分量中的噪声含量。
奇异值分解;构造信号;叠加信号;模态混叠;噪声含量
液压信号可以看成是由若干个不同频率的频率族分量组成,而每一个频率族的分量所对应的幅值可以看成是调幅信号[1],将这些成分单独地分开是后续处理过程的关键步骤,在将液压信号分解到不同的频率通道中的研究中,主要有以下两种方法:
(1) 小波分解及小波包分解。不同于小波分解仅对低频部分继续分解,小波包分解兼对低频和高频部分实施分解,以获得更高的频率分辨率。当需要获得信号在一个频段的时间序列的时候,可以重构该频段的分解系数获得。但是限于怎样合适选取小波基函数及特定基函数对于特定信号是否适用,使得小波分解及小波包分解的应用于实测信号存在困难。
(2) EMD(Empirical Mode Decomposition)及其改进方法。EMD是由Huang等[2-3]提出的一种信号的时域分解方法,信号通过EMD被分解成一系列内禀模态函数 (Intrinsic Mode Function, IMF),这些IMF含有特定的频率成分。在处理实测信号时,EMD主要存在两点缺陷:
①模态混叠 (Mode Aliasing)。EMD分解的最理想的效果是每个IMF分量中仅含有一种频率成分。而实测信号在分解时常会出现单个IMF分量中存在多个频率成分,或者单个频率成分会发散到不同的IMF分量中的现象,即模态混叠。为了改善模态混叠,Wu等[4]提出的EEMD (Ensemble Empirical Mode Decomposition)通过向原信号中加入多组白噪声分解后再求平均的方法来抑制该缺陷,但该方法面临着如何合适选取噪声组数和方差的困难;Ryan等[5]提出掩膜信号法,通过对原信号分别加上和减去一个掩膜信号分别进行EMD分解,再对IMF分量做平均,赵玲等[6]对平均瞬时频率进行修正来改进掩膜信号,但是针对不同的信号需要确定不同的掩膜信号,而且用希尔伯特变换估计出的瞬时频率偏差比较大,该方法对分离振幅和频段比较接近的信号效果并不好。
②IMF分量中噪声含量较高。分解得到的IMF分量中有的分量的幅值谱中的波峰向两边发散较大,分量中参杂了不必要的噪声成分。实际操作时,为了有效降低IMF分量中的噪声含量,往往对实测信号先降噪,再分解。
奇异值分解 (Singular Value Decomposition, SVD)是一种通过矩阵运算对信号进行处理的方法,根据Hankel矩阵构造形式将一维信号构造成信号矩阵,该矩阵通过奇异值分解被分解成两个酉矩阵和一个对角阵的乘积,该方法在信号处理尤其是信号降噪中有着广泛的使用[7-12]。其中最具代表性的是赵学智等人提出的奇异值差分谱降噪方法,该方法合理地选择了有效重构奇异值的阶数,很好地从含噪信号中还原出理想信号。
根据奇异值分解的相关特性,本文提出了一种液压信号的时域分解方法。该方法根据原信号中某一频率的构造一相同频率、振幅已知的周期信号,与原信号叠加,使得叠加信号中该频率对应的奇异值所在阶数可以确定,继而选取这些阶数上奇异值重构出叠加信号中该频率的时间序列,再减去加入的周期信号,最终还原出原信号中该频率的时间序列。在与EMD进行比较后,发现该方法不仅有效消除了模态混叠,而且降低了分量中的噪声含量。
1 奇异值分解及其差分谱理论
1.1 奇异值分解理论
实测信号x可以根据Hankel矩阵形式被构造成一个m×n的信号矩阵Hx,矩阵构造形式为
(1)
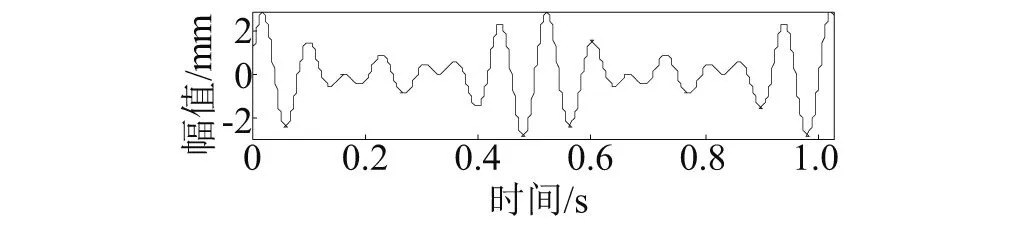
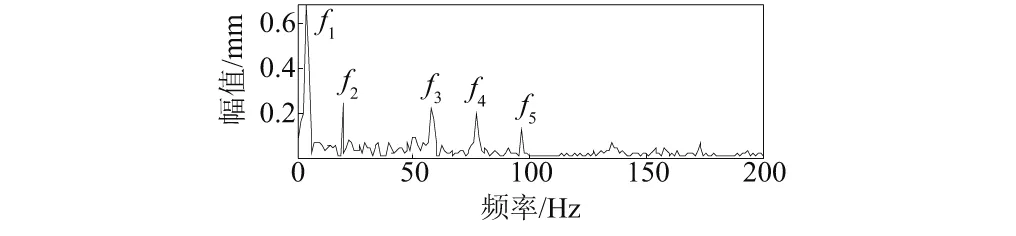
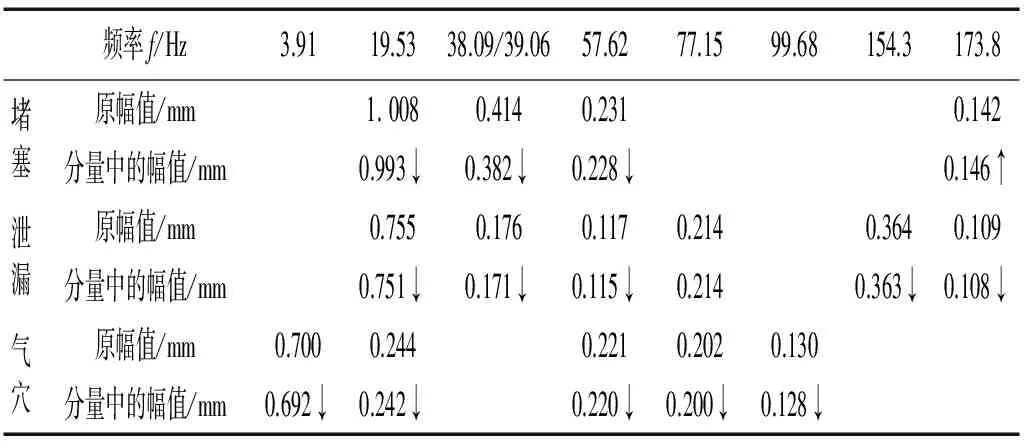
式中:N为x的长度;1 对Hx进行奇异值分解 Hx=USVT (2) 式中:U为m×m的酉矩阵;S为m×n的对角矩阵;V为n×n的酉矩阵。其中S可表示为 (3) 式中:∑=diag(σ1,σ2,…,σr) (σ1>σ2>…>σr>0)。 这种变换的本质是将原始信号分解为一系列分量信号的简单线性叠加,而这一系列分量可以通过单独选取S中的对角线上的单个奇异值重构获得,而且重构出的信号的相位和它在原信号中叠加的相位是不变的,即具有零相位偏移特性。 1.2 奇异值差分谱理论 奇异值分解被有效用于信号的降噪中,在文献[13]中,定义差分值bi来描述σi的变化情况 bi=σi-σi+1(1 (4) 式中,min(m,n)为Hankel矩阵行数和列数中的较小值。当bi达到最大值时,此时奇异值σi所代表的分量实现了从有用信号分量向噪声分量的转变,接下来选取该点及其之前的奇异值为有效奇异值,其他奇异值置零,然后通过式(2)重构出降噪后的信号矩阵,再重排矩阵元素获得降噪信号。 2.1 方法的提出 本文提出的方法旨在消除分量中模态混叠,这就要求待分解的原信号必须是平稳信号,因为平稳信号中的频率具有可数性和时不变性的特点,这就给原信号中不同频率能够被单独分开提供了可能;同时原信号的截取应满足采样定理和足够的采样长度,这样生成的序列才能重现振动波形中的所有频率成分及获得较高的频率分辨率。文章开始提到液压信号可以看成由不同频率族分量的调幅信号组成,表示液压信号同样是平稳信号,适合用本文提出的方法进行分解。 通过钱征文等[14]的研究和相关实验,总结出奇异值分解在处理平稳信号时存在以下两点性质: (1) 当原信号中除噪声外仅含有一个频率成分,该信号的Hankel矩阵经分解后得到的对角阵S的前两阶的奇异值较大,而其他阶奇异值很小;当除噪声外含有两个频率成分,分解后S的前4阶的奇异值较大,而其他阶奇异值很小。依此类推:当原信号除噪声外含有k个频率成分,经分解后S的前2k阶奇异值较大,其他阶奇异值较小。而对于信噪比较高的信号,仍然满足上述规律。 (2) 成对出现的奇异值的大小与该频率的振幅呈正相关,即某频率的振幅越大,经分解后在S中得到的奇异值越大,它们在S中所处的阶数越靠前。而奇异值大小与频率大小无明显关系。 现构造y1对以上性质加以说明,y1中含有4个分量,分量1是频率10 Hz,振幅为1的正弦分量;分量2是频率为20 Hz,振幅为2的正弦分量;分量3是频率为30 Hz,振幅为3的正弦分量;分量4是均值为0,方差为1的白噪声。y1的采样频率为1 000 Hz,含有1 024个采样点。图1是y1及其各分量的时域图。 y1=sin(20πt)+2sin(40πt)+3sin(60πt)+wn (5) 图1 y1及各分量的时域图Fig.1 y1’s components’ time-domain plots 构造y1的Hankel矩阵并对其进行奇异值分解,获得U1、S1和V1。画出S1对角线上奇异值随其所在阶数的变化火柴梗图,如图2所示。 图2中可以发现,前6阶奇异值(772.34、762.55、520.89、506.16、256.98、250.05)的数值比较大,为有用信号的奇异值,而之后的奇异值很小,为噪声成分的奇异值。而且前6阶奇异值可以很明显地分成3组:772.34和762.55为一组;520.89和506.16为一组;256.98和250.05为一组。由前述的奇异值分解的性质可得:这3组奇异值由3个频率成分分解获得,而且这3个频率成分的振幅依次递减。再参照的的频率组成可以确定:772.34和762.55是30Hz分量的奇异值,520.89和506.16时20Hz分量的奇异值,256.98和250.05为10Hz分量的奇异值。 图2 奇异值-阶数变化图Fig. 2 Singular value-order plot 分别选取前3对奇异值重构出3个时间序列,图3为3个序列时域图及幅值谱。从图3中可以明显看出3个序列各自对应着y1中的30Hz、20Hz和10Hz的频率成分,和前面的结论相吻合。 从上述过程可以看出,奇异值大小对振幅的分辨是敏感的,假设原信号中某个频率成分的振幅最大,且在数值上较其他频率的振幅占有绝对优势,那么该成分对应的奇异值一定位于对角阵S的前两阶,此时只要选取S的前两阶就可以重构出该频率的时间序列。但是实测信号中也可能存在振幅相当的频率成分,这样它们对应的奇异值大小也就难以区分。 图3 3组奇异值重构出的时间序列的时域图及幅值谱Fig.3 Time-domain plots and amplitude spectrums of three pairs singular values 拟定任意平稳信号x的分解步骤 步骤1 从x的时域图上得到它的振幅A,从幅值谱上准确得到其频率成分f1、f2、…、fk(f1 (6) (7) 步骤4 构造xnew的Hankel矩阵Hnew,对其进行奇异值分解,获得两个酉矩阵Unew和Vnew,一个对角矩阵Snew。 步骤5 选取Snew中的前两阶奇异值重构出一个信号xb1,xb1是叠加信号xnew中f1对应的时间序列。 (8) 步骤7 针对f2,重复步骤1~步骤6,最终得到原信号中fi(i=1,2,…,k)对应的时间序列xi(i=1,2,…,k)。 2.2 基于仿真信号的性能检验 实验发现,EMD在分解含有频率成分较接近的信号时易产生模态混叠,因此构造信号y2(见图4)。 图4 y2的时域图Fig. 4 y2’s time-domain plots y2中含有10Hz、12Hz和14Hz的频率成分,且各成分振幅均为1。该信号含1 024个采样点,采样频率为1 000Hz。 y2=sin(20πt)+sin(24πt)+sin(28πt) (9) 先对y2进行EMD分解,图5为IMF分量的时域图和幅值谱。从图5(b)中明显地看出IMF1和IMF2中出现严重的模态混叠。 再对y2用提出方法进行分解,先从时域图上得到y2的振幅为A2=2.93。据式(6)构造一个频率为10Hz (10) 图6为xi、x2、x3的时域图和幅值谱。从图6(b)中可以看出每个幅值谱明显只含有一种频率成分,不存在模态混叠。且各频率依次为10Hz、12Hz、14Hz,和原信号中的频率成分吻合。且图6(a)中xi的振幅都稳定在1处,和原信号中的各频率振幅一致。 图5 IMF分量的时域图和幅值谱Fig.5 IMF’s time-domain plots and amplitude spectrums 图6 xi的时域图和幅值谱Fig.6 xi’s time-domain plots and amplitude spectrums 2.3 基于液压信号的性能检验 实验所用的液压综合试验台上分布着泄漏控制阀、调速阀、气穴控制阀和堵塞控制阀等。通过不同阀门的是否开合,开合大小的控制,来实现液压系统不同工况的控制。图7为实验现场图和传感器布置图。实验采用121A100型压电式IEPE加速度传感器通过EMT690D信号采集仪与电脑连接。如图7(b)中A点所示,传感器通过磁力吸附在液压缸的水平方向,来测取物块提升过程中液压缸的振动信号。 图7 实验相关图片Fig.7 Experiment related pictures 分别测得液压缸在堵塞,泄漏,气穴工况的振动信号,y3,y4,y5是从3个信号中截取出的1 024个连续信号点,采样频率为1 000Hz,它们的时域图如图8所示。 (a) 堵塞信号y3 (b) 泄漏信号y4 (c) 气穴信号y5图8 不同状态下信号的时域图Fig.8 Signals of different status in time domain 2.3.1 堵塞信号y3的分解 (1) 本文提出的方法 作y3的幅值谱如图9所示。 图9 y3的幅值谱Fig.9 y3’s amplitude spectrum 从图9中精确地得出幅值谱中的明显频率成分,分别为19.53Hz、38.09Hz、57.62Hz和173.80Hz,对应图9中的f1、f2、f3、f4。再从图8(a)中得到y3的振幅A3=2.28。 (11) 图10中可以看出y3被单独分解成了4个分量,不存在模态混叠。4个频率分别是19.53 Hz、38.09 Hz、57.62 Hz和173.80 Hz。和图9中y3的幅值谱中的主要频率成分吻合,而且每个频率的幅值和图9中各频率幅值相当,每个频率被极大地提取出来。同时各分量的频域谱线比较平滑,噪声含量比较小。 (2) EMD分解 对y3先用小波阈值降噪后再进行EMD分解,得到一组IMF分量。图11为IMF分量的时域图和幅值谱。从图11(b)中可以看出:①IMF1和IMF2发生了模态混叠;②IMF分量的频域图比较散乱,分量中噪声含量较高。 图10 xi的时域图和幅值谱Fig.10 xi’s time-domain plots and amplitude spectrums 图11 IMF分量的时域图和幅值谱Fig.11 IMF’s time-domain plots and amplitude spectrums 2.3.2 泄漏信号y4的分解 (1) 本文提出的方法进行处理。 作y4的幅值谱如图12所示。 图12 y4的幅值谱Fig.12 y4’s amplitude spectrum 从图12中精确地得出幅值谱中的明显频率成分,分别为19.53 Hz、39.06 Hz、57.62 Hz、77.15 Hz、154.30 Hz和173.80 Hz,对应图12中的f1、f2、f3、f4、f5、f6。再从图8(a)中得到y4的振幅A4=1.63。用提出的方法对y4进行分解,得到分量xi(i=1,2,…,6)。图13为xi的时域图和幅值谱。从图中看出,经分解后y4中的6个频率成分被单独分开,不存在模态混叠,且各频率成分保持了原信号中的幅值,分量的频域谱线仍比较光滑,噪声含量较小。 (2) EMD分解。 对y3先用小波阈值降噪后再进行EMD分解,得到一组IMF分量。图14为IMF分量的时域图和幅值谱。从图14(b)中可以看出IMF1和IMF2中存在着模态混叠,同时分量的频域谱线仍比较杂乱,噪声含量较高。 图13 xi的时域图和幅值谱Fig.13 xi’s time-domain plots and amplitude spectrums 图14 IMF分量的时域图和幅值谱Fig.14 IMF’s time-domain plots and amplitude spectrums 2.3.3 气穴信号的分解 (1) 本文提出的方法进行处理。 作y5的幅值谱如图15所示。 图15 y5的幅值谱Fig.15 y5’s amplitude spectrum 从图15中精确地得出幅值谱中的明显频率成分,分别为3.91 Hz、15.93 Hz、57.62 Hz、77.15 Hz和99.68 Hz, 对应图15中的f1、f2、f3、f4、f5。再从图8(a)中得到y5的振幅A4=1.94。用提出的方法对y5进行分解,得到分量xi(i=1,2,…,5)。图16为xi的时域图和幅值谱。经分解,y5中的5个频率成分被单独分开,不存在模态混叠,且各频率成分保持了原信号中的振动幅值,同样各分量中噪声含量较小。 (2) EMD分解。 对y5先用小波阈值降噪后再进行EMD分解,得到一组IMF分量。图17为IMF分量的时域图和幅值谱。从图17(b)中可以看出IMF1和IMF2中存在着模态混叠,同时分量的频域谱线仍比较杂乱,噪声含量较高。 图16 xi的时域图和幅值谱Fig.16 xi’s time-domain plots and amplitude spectrums 图17 IMF分量的时域图和幅值谱Fig.17 IMF’s time-domain plots and amplitude spectrums 综合液压系统的三种工况的分解结果,将各工况下的原信号和分量中频率及其幅值汇总至表1。 从表1中可以看出: (1) 原信号经分解后,分量中的频率幅值都略有减小(用下降箭头标出),这是因为分解时每次仅选取前两个较大的奇异值重构,而代表噪声的小奇异值没有参与重构,噪声一直被压制在剩余信号中,从而减小了噪声在幅值谱中的叠加。 (2) 对比不同工况下的频率组成,堵塞、泄漏信号含有四个相同的频率(38.09Hz和39.06Hz被视为同一频率),但是泄漏信号多出了77.15Hz的中高频分量和154.3Hz、173.8Hz的高频分量,这就导致泄漏状态下的执行装置的提升声音更加尖锐。而气穴信号相比其他两种工况出现了幅值较大的3.91的低频分量,导致气穴状态的工作声音比较低沉。 表1 不同状态下原信号和分量中频率及其幅值 本文利用奇异值分解中奇异值对不同频率振幅大小的分辨能力,提出了一种基于奇异值分解的液压信号的时域分解方法,方法根据原信号的频率组成,依次向其中叠加频率相同、振幅已知的周期信号,再选取特定的奇异值重构,最终还原出每个频率的时间序列。 分别通过仿真信号和液压信号对该方法性能进行验证,并与EMD的分解结果就模态混叠和噪声含量做了比较。本文提出的方法不仅消除了分量中模态混叠,而且抑制了分量中的噪声含量。 [ 1 ] 唐宏宾, 吴运新, 滑广军,等. 基于EMD包络谱分析的液压泵故障诊断方法[J]. 振动与冲击, 2012, 31(9): 44-48.TANG Hongbin, WU Yunxin, HUA Guangjun, et al. Fault diagnosis of pump using EMD and envelope spectrum analysis[J]. Journal of Vibration and Shock, 2012, 31(9): 44-48. [ 2 ] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]// Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society, 1998:903-995. [ 3 ] HUANG N E, WU Manli, QU Wendong, et al. Applications of Hilbert-Huang transform to non-stationary financial time series analysis[J]. Applied Stochastic Models in Business and Industry, 2003, 19(3): 245-268. [ 4 ] WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. [ 5 ] RYAN D, KAISER J F. The use of a masking signal to improve empirical mode decomposition[C]// International Conference on Acousic, Speech and Signal Processing 2005 IEEE. Cambridge: MIT Press, 2005: 485-488. [ 6 ] 赵玲, 刘小峰, 秦树人,等. 消除经验模态分解中混叠现象的改进掩膜信号法[J]. 振动与冲击, 2010, 29(9): 13-17. ZHAO Ling, LIU Xiaofeng, QIN Shuren, et al. Use of masking signal to improve empirical modede composition[J]. Journal of Vibration and Shock, 2010, 29(9): 13-17. [ 7 ] HASSANPOUR H, ZEHTABIAN A. Time domain signal enhancement based on an optimized singular vector denoising algorithm[J]. Digital Signal Processing, 2012, 22(5): 786-794. [ 8 ] 刘鎏, 闫云聚, 李鹏博. 奇异谱分解在超声速无人机声振试验数据处理中的应用[J]. 振动与冲击, 2015, 34(3): 28-34. LIU Liu, YAN Yunju, LI Pengbo. Singular value spectral decomposition and its application in acoustic vibration test data processing of a supersonic aircraft[J]. Journal of Vibration and Shock, 2015, 34(3): 28-34. [ 9 ] 刘敏, 张英堂, 李志宁,等. 基于自适应奇异值标准谱和 EMD 的柴油机故障诊断[J]. 车用发动机, 2015(2): 77-82. LIU Min, ZHANG Yingtang, LI Zhining, et al. Diesel engine fault diagnosis based on adaptive sigular value stantard spectrum and empirical mode decomposition[J]. Vehicle Engine, 2015(2): 77-82. [10] 王超, 孔凡让, 黄伟国,等. 改进的奇异值分解在轴承故障诊断中的应用[J]. 振动工程学报, 2014, 27(2): 296-303. WANG Chao, KONG Fanrang, HUANG Weiguo, et al. Application of improved singular value decompostion in bearing fault diagnosis[J]. Journal of Vibration Engineering, 2014,27 (2): 296-303. [11] 胥永刚, 谢志聪, 孟志鹏,等. 基于奇异值分解的磁记忆信号特征提取方法[J]. 振动、测试与诊断, 2014, 34(6): 1105-1109. XU Yonggang, XIE Zhicong, MENG Zhipeng, et al. Feature extraction method of magnetic memory signal based on SVD[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(6): 1105-1109. [12] 徐彦凯, 双凯. 自适应奇异值分解瞬变信号检测研究[J]. 电子与信息学报, 2014, 36(3): 583-588. XU Yankai, SHUANG Kai. Detection of transient signal based on adaptive singular value decomposition[J]. Journal of Electronics & Information Technology,2014, 36(3): 583-588. [13] 赵学智, 叶邦彦, 陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报, 2010, 46(1): 100-108. ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Journal of Mechanical Engineering, 2010, 46(1): 100-108. [14] 钱征文, 程礼, 李应红. 利用奇异值分解的信号降噪方法[J]. 振动、测试与诊断, 2011, 31(4): 459-463. QIAN Zhengwen, CHENG Li, LI Yinghong. Noise reduction method based on singular value decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 459-463. A hydraulic signal decomposition method based on singular value decomposition ZHANG Xiaoming, TANG Jian, ZHANG Meijun (Engineering Institute of Engineering Corps, PLA University of Science and Technology, Nanjing 210007, China) In order to suppress the mode aliasing phenomenon and reduce noise composition, a signal decomposition method in time domain based on singular value decomposition (SVD) was proposed. Based on two features of SVD, firstly each frequency corresponds to two sizeable singular values. Secondly singular values are positively related to the amplitude of its corresponded frequency. The method was conducted by adding a known simulation sine signal with appropriate amplitude to make the location of singular values easier to be identified. Then, time series were reconstructed by choosing related singular values. Finally, the time series of a certain frequency could be achieved by subtracting added simulation signal. By comparing with the EMD, it is effectively confirmed that the method can both eliminate mode aliasing and reduce noise composition. singular value decomposition; construct signals; superposition of signals; mode aliasing; noise composition 国家自然科学基金 (51175511;61472392);省青年基金(BK20150724) 2016-03-21 修改稿收到日期: 2016-06-28 张小明 男,硕士生,1991年12月生 唐建 女, 硕士生导师, 1977年1月生 TH137 A 10.13465/j.cnki.jvs.2017.16.015
2 基于奇异值分解的信号时域分解方法






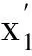
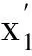
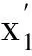







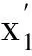

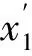







3 结 论
