SH波斜入射时有阻尼成层介质自由场的一维化时域算法

高智能， 卓卫东，2， 谷 音，2

(1. 福州大学 土木工程学院，福州 350116； 2. 福州大学 福建省土木工程多灾害防治重点实验室，福州 350116)

SH波斜入射时有阻尼成层介质自由场的一维化时域算法

高智能1， 卓卫东1，2， 谷 音1，2

(1. 福州大学 土木工程学院，福州 350116； 2. 福州大学 福建省土木工程多灾害防治重点实验室，福州 350116)

在进行大型大跨结构抗震设计时，需要考虑地震波斜入射的影响。在刘晶波等提出的一维化时域算法基础上，采用有限差分方法，推导建立了SH波斜入射情形下、考虑阻尼影响的水平成层弹性介质出平面自由场求解的显式数值逐步法公式，并采用Fortan程序语言编制了相应的数值计算程序。综合采用有限元法和数值逐步法，进行SH波斜入射下单层土和双层土的算例分析。结果表明：土层介质阻尼仅影响到SH波斜入射下自由场的位移幅值，而对位移时程的波形没有影响；SH波斜入射下有阻尼与无阻尼情形相比位移幅值有明显衰减，对单层土，30°斜入射下衰减幅度可达40.5%；对双层土，最大衰减幅度可达39.7%；有阻尼土层位移幅值的衰减幅度从底部边界向自由表面逐渐增大。

成层介质；出平面波动；斜入射；一维化时域算法；介质阻尼；逐步法

已有研究表明，地震波斜入射引起的地面运动非一致变化对地铁车站、长大桥梁、大坝等大型大跨结构的地震响应有较大的影响[1-4]。因此，有必要在这类结构的抗震设计中考虑地震波斜入射的影响。在实际工程中，由于土层分布的复杂性，对地震波斜入射下土层自由场的解析求解几乎是不可能的[5-6]。因此，采用各种数值方法，研究复杂土层介质中的地震波动问题，已经成为主要的研究方向。

实际大型大跨结构基础所在的土层往往被假定为水平成层介质；对水平成层弹性半空间，地震波斜入射下自由场的计算可在频域内实现[7-8]。然而，为获得地震动时程，频域方法需要进行多次快速Fourier变换，这会消耗大量的计算机存储空间和计算时间。针对频域方法的不足，李山有等[9]根据地震波斜入射情形下水平成层弹性半空间波动传播水平视波速不变且已知的特点，采用透射边界[10]模拟远场对有限域的影响，建立了入射侧边界节点自由场计算的精确内插公式，并将其与计算内节点位移的显式差分公式相结合，得到了地震波斜入射下无阻尼水平成层弹性半空间人工边界节点自由场的时域计算方程，可用于近场波动数值模拟中内行波场与散射波场的时域同步模拟。刘晶波等[11-13]进一步提出一种一维化的时域算法，将地震波斜入射下水平成层弹性半空间自由场的计算问题简化为时域内的一维问题求解，且具有与二维有限元数值解同样的精度。赵密等[14]在刘晶波等算法的基础上，提出一种模拟基岩半空间辐射阻尼的人工边界条件，采用该人工边界条件代替黏性边界条件，提高了大角度斜入射下平面内自由波场的计算精度。为了改善显式有限差分时域算法的局限性，范留明等[15]基于惠更斯波动观点，提出一种称为“界面子波算法”的新的时域数值方法，可求解成层弹性半空间出平面一维自由场。王笃国等[16]基于一维等效线性化频域方法，利用成层弹性介质频域传递矩阵，推导了等效剪应变公式，提出一种可计算地震波斜入射下成层介质非线性自由场的数值方法。

已有关于地震波斜入射情形下水平成层弹性半空间自由场的显式有限差分时域算法，均未考虑土层介质阻尼的影响。然而，土层介质阻尼可能对地震波斜入射下土层介质的自由场有重要的影响。本文在刘晶波等算法的基础上，考虑土层介质阻尼，综合采用有限元法与有限差分法，推导建立SH波斜入射下水平成层弹性介质出平面自由场求解的数值逐步法公式，并编制相应的数值计算程序；通过算例分析，讨论土层介质阻尼对SH波斜入射情形下水平成层弹性介质出平面自由场的影响。

1 成层半空间出平面波动问题的一维化

在地下土层自由场的计算中，通常将土层介质假设为由下卧弹性半空间(基岩)和其上的水平成层弹性介质(土层)组成，各层的质量密度和剪切波速分别为ρl和csl(l=1,2,…,L)。按照刘晶波等提出的一维化算法的思路，将水平成层弹性半空间划分为如图1所示的有限元离散化模型；图1中，竖向网格尺寸为Δy，可取为满足精度要求的任意值；水平方向网格尺寸为Δx，其取值需满足式(1)

Δx=cx·Δt

(1)

式中：cx为入射SH波的水平视波速；Δt为时间步长。

图1 水平成层半空间有限元模型Fig.1 Finite element model of the layered half-space

(2)

式中，Mi,j、Ci,j和Ki,j分别为与节点(i,j)相关的集中质量系数、阻尼系数和刚度系数。

由式(2)可见，节点(m,n)的运动只与该节点直接相邻的节点运动有关。在弹性介质中，沿水平方向的波动为行波，波速为视波速cx，因此，弹性介质内的波场可以表示为

(3)

若取时间步长为Δt，则由式(3)可以得到式(4)

u(x+jcxΔt,y,t)=u(x,y,t-jΔt) j∈(-∞,∞)

(4)

对图1中的各离散节点，利用式(4)可得到

(5)

当i=±1时，由式(5)有

(6)

同理，节点速度和加速度同样存在以上关系。由式(6)可见，与节点(m,n)直接相邻的同一层节点(m-1,n)和节点(m+1,n)在pΔt时刻的运动可用节点(m,n) 在相邻时刻的运动来表示。

综合式(2)和式(6)可见，节点(m,n)在pΔt时刻的运动方程式(2)中，未知量仅包含第m列节点在pΔt及其相邻时刻的运动。在求得第m列节点位移之后，根据式(3)即可确定整个半空间中的自由场。如此，SH波斜入射下水平成层弹性半空间出平面自由场的计算问题就转化为一维问题求解。

2 考虑介质阻尼的一维化时域算法

2.1 考虑介质阻尼的数值逐步法的计算公式

首先，采用刘晶波等算法的思路，将SH波斜入射下水平成层弹性半空间出平面自由场的计算问题转化为一维问题。其次，综合采用有限元法与有限差分法，在时域内直接求解式(2)所列的运动方程。在数值计算中可取m=0，即先求得y轴上各节点的位移，再根据式(3)，依次确定水平成层弹性半空间中的自由场。以下，采用有限差分方法，推导建立考虑土层介质阻尼时求解y轴上各节点位移的计算列式。

根据式(2)，在考虑土层介质阻尼时，y轴上任一内节点(0,n)在pΔt时刻的运动方程为

(n=1,2,…,N-1)

(7)

式中，M0,n为节点(0,n)的集中质量。

y轴与自由表面交界处的节点(0,0) 在pΔt时刻的运动方程为

(8)

式中，M0,0为节点(0,0)处的集中质量。

在采用数值方法计算水平成层弹性半空间的自由场时，显然必须从半无限介质中切取有限的计算区域，并在区域边界引入合适的人工边界条件。目前已发展了多种人工边界[17-26]，不失一般性，本文假定人工边界为黏性边界。对y轴与黏性边界交界处的节点(0,N)(设为节点B)，其在pΔt时刻的运动方程为

(9)

(10)

式中：ρ为介质质量密度；cs为介质剪切波速；θ为地震波入射角；w0(xB,yB,t)和τ0(xB,yB,t)分别为入射波在黏性边界节点B上产生的位移和应力。

式(7)～式(9)所列的运动方程中的加速度项可利用中心差分法近似计算

(11)

(12)

考虑式(6)，同时将式(11)和式(12)代入式(7)～式(9)中，并简记u0,n=un，M0,n=Mn，经整理得到如下矩阵形式的方程

(13)

(14a)

(14b)

从式(14)可见，式(13)所列的矩阵方程左边的系数矩阵是稀疏的三对角矩阵，右边的向量仅与边界节点输入的等效荷载以及y轴上各节点在pΔt时刻及其前一时刻(p-1)Δt的位移有关，故只要给定边界节点等效荷载以及初始时刻各节点的位移和速度值，即可通过逐步法求解上述方程组，得到轴上各节点在时域内的位移解，进而确定全部自由场。

2.2 计算步骤及程序实现

由式(13)所列的矩阵方程可见，本文基于有限差分方法建立的考虑介质阻尼的水平成层弹性介质自由场的数值逐步法的计算公式是显式的，因此，求解容易实现。具体计算步骤如下：

步骤1 对选取的计算区域进行离散化(见图1)，采用有限元法计算离散化模型的质量矩阵M和刚度矩阵K，其中质量矩阵M采用集中质量法计算，并假定阻尼矩阵C。

步骤2 根据黏性人工边界条件，确定人工边界节点等效荷载时程。

(15)

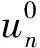
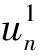
步骤6 由式(3)，确定计算区域内各节点的自由场。

根据上述计算步骤，基于Fortran语言编制了相应的计算程序。限于篇幅，这里没有给出计算程序的源代码。

2.3 算法的稳定性和计算精度

本文所建立的SH波斜入射下考虑介质阻尼的水平成层弹性介质出平面自由场的一维化时域算法，其稳定性条件仍与刘晶波等算法的稳定性条件相同，即要求

(16)

文献[11]分析表明，当时间步长满足式(16)所表示的稳定性条件时，一维化时域算法对于不同方向的入射波都有很高的计算精度。

3 算例分析

以下选择物理性质均匀的单一土层(下文简称单层土)和基岩表面覆盖软土层(下文简称双层土)这两种情形分别进行分析。算例分析中，均假定土层和基岩介质阻尼为Rayleigh阻尼。因而，可按下式计算其阻尼矩阵C[27]

C=αM+βK

(17)

式中，α、β为比例系数，它们由式(18)计算

(18)

式中：ωi和ωj分别为两个特定的自振圆频率；ξi和ξj分别为与ωi和ωj相关的模态阻尼比。

3.1 单层土算例分析

假定单层土由半无限空间的均匀弹性土层组成，其几何参数和物理参数取值如表1所列，计算区域yb取为100 m。计算区域的有限元离散化模型如图2所示，其中竖向网格尺寸Δy取为5 m，水平方向网格尺寸Δx根据式(1)确定。在计算区域的底部边界引入人工黏性边界条件，并假定在黏性人工边界处入射SH波为持时0.5 s、峰值1 cm的Dirac函数形式的单位脉冲，其位移时程如图3所示。在数值计算中，为满足稳定性条件，时间步长取为0.005 s，持时取为2.5 s。

表1 单层土模型参数

图2 单层土有限元离散化模型Fig.2 FEM model of one-layer soil

图3 黏性边界节点C1处入射的SH波位移时程Fig.3 Displacement time history of incident SH wave at boundary joint C1

利用ABAQUS软件建立计算区域的有限元模型，计算得到单层土模型的质量矩阵M和刚度矩阵K；通过动力特性分析，得到该单层土模型前两阶的自振频率：ω1=8.864 5rad/s，ω2=10.028 0rad/s；将其代入式(18)，并取单层土模态阻尼比ξ1=ξ2=ξ=0.1，求得α=0.941 2，β=0.010 58；将α、β的数值代入式(17)，得到单层土模型的阻尼矩阵C。

利用所编制的计算程序，计算了SH波以30°斜入射情形下单层土模型的自由场。选取y轴上自由表面节点A1、中部节点B1以及底部边界靠内侧节点C1作为观测点(见图2)，对计算结果进行分析讨论。由于无阻尼情形下一维化算法的计算结果已得到验证，这里主要讨论考虑土层介质阻尼情形下一维化算法的计算结果。

图4绘出了SH波以30°斜入射情形下，采用一维化算法计算得到的无阻尼和有阻尼单层土模型在3个观测点处的位移响应。从图4中可以发现，无阻尼与有阻尼均匀单层土的位移时程曲线波形一致；有阻尼与无阻尼均匀单层土相比，前者在各个时刻的位移响应绝对值均减小了，尤其在自由表面观测点A1处，位移幅值衰减幅度最大。这说明土层介质阻尼仅影响到位移幅值，而对位移时程的波形没有影响。

(a) 观测点A1位移时程的计算结果

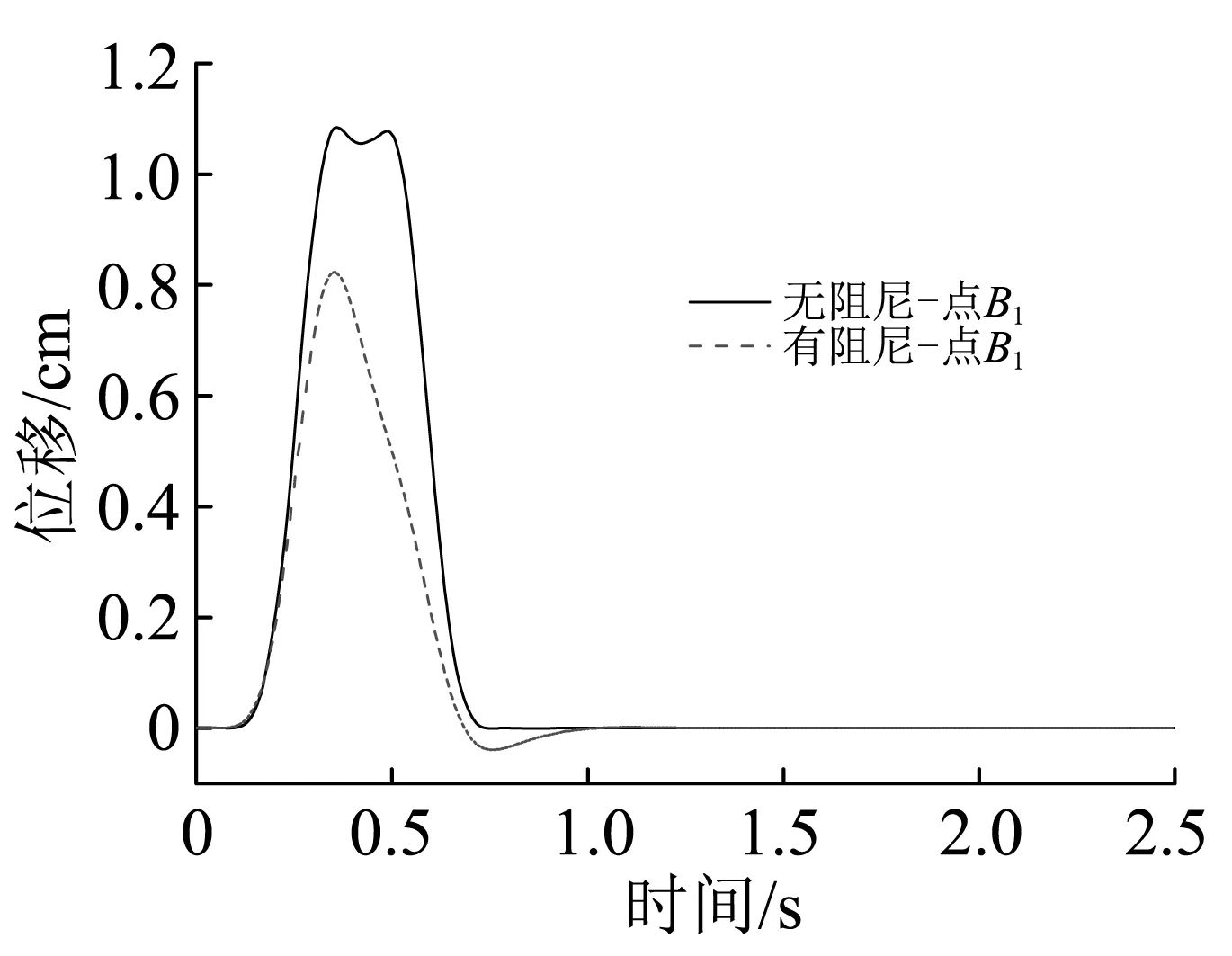
(b) 观测点B1位移时程的计算结果

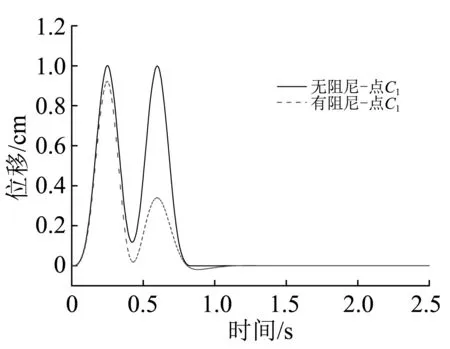
(c) 观测点C1位移时程的计算结果

图4 SH波30°斜入射时无阻尼和有阻尼单层土的位移响应比较

Fig.4 Comparison between the displacement response of the one-layer soil with and without damping by incident SH wave at 30°

根据计算结果，无阻尼与有阻尼均匀单层土相比，自由表面观测点A1处的位移幅值从2.00 cm减小至1.19 cm，衰减幅度达40.5%；中部观测点B1的位移幅值从1.08 cm减小至0.82 cm，衰减幅度达24.1%；底部观测点C1的位移幅值从1.00 cm衰减至0.92 cm，衰减幅度达8.0%。可见，SH波斜入射下土层介质阻尼显著影响到均匀单层土自由场的位移幅值，且其影响程度从底部边界向自由表面逐渐增大。

3.2 双层土算例分析

假定双层土由下卧半无限空间的基岩和上覆50 m厚的均匀土层组成，其几何参数和物理参数取值如表2所列，计算区域yb取为100 m。计算区域的有限元离散化模型如图5所示，其中竖向网格尺寸Δy取为5 m，水平方向网格尺寸Δx根据式(1)确定。在计算区域的底部边界引入人工黏性边界条件，同样假定在黏性人工边界处入射SH波为持时0.5 s、峰值1 cm的Dirac函数形式的单位脉冲，其位移时程见图3。为满足稳定性条件，时间步长取为0.005 s，持时取为2.5 s。

首先，利用ABAQUS软件建立计算区域的有限元模型，计算得到双层土模型的质量矩阵M和刚度矩阵K；进而得到上覆均匀土层和下卧基岩层的质量子矩阵MS和MR，以及刚度子矩阵KS和KR。

表2 双层土模型参数

图5 双层土有限元离散化模型Fig.5 FEM model of two-layer soil

对双层土模型，可假定均匀土层和基岩介质阻尼为Rayleigh阻尼；然而，考虑到土层和基岩层阻尼机制不同，双层土模型的阻尼矩阵C需要采用非比例阻尼矩阵构造。通过动力特性分析，得到该双层土模型前两阶的自振频率：ω1=13.585 0 rad/s，ω2=16.258 0 rad/s；取上覆均匀土层的模态阻尼比ξS1=ξS2=ξS=0.1，取下卧基岩层的模态阻尼比ξR1=ξR2=ξR=0.03，分别将其代入式(18)，求得均匀土层和基岩层的比例系数分别为αs=1.480 3，βs=0.006 7，以及αR=0.444 2，βR=0.002 0；将质量子矩阵MS、MR和刚度子矩阵KS、KR以及各自的比例系数代入式(17)，得到上覆均匀土层和下卧基岩层各自的阻尼矩阵CS和CR；通过有限元直接集装方法，得到双层土离散化模型的阻尼矩阵C。上述过程均可通过ABAQUS软件实现。

在得到双层土模型的质量矩阵M、刚度矩阵K和阻尼矩阵C后，利用所编制的计算程序，计算了SH波以不同入射角入射情形下双层土模型的自由场；所取的入射角变化范围为0°～90°，并以15°为间隔。选取y轴上自由表面节点A2、中部节点B2以及底部边界靠内侧节点C2作为观测点(见图5)，对计算结果进行分析讨论。同样地，由于无阻尼情形下一维化算法的计算结果已得到验证，这里也主要讨论考虑土层介质阻尼情形下一维化算法的计算结果。

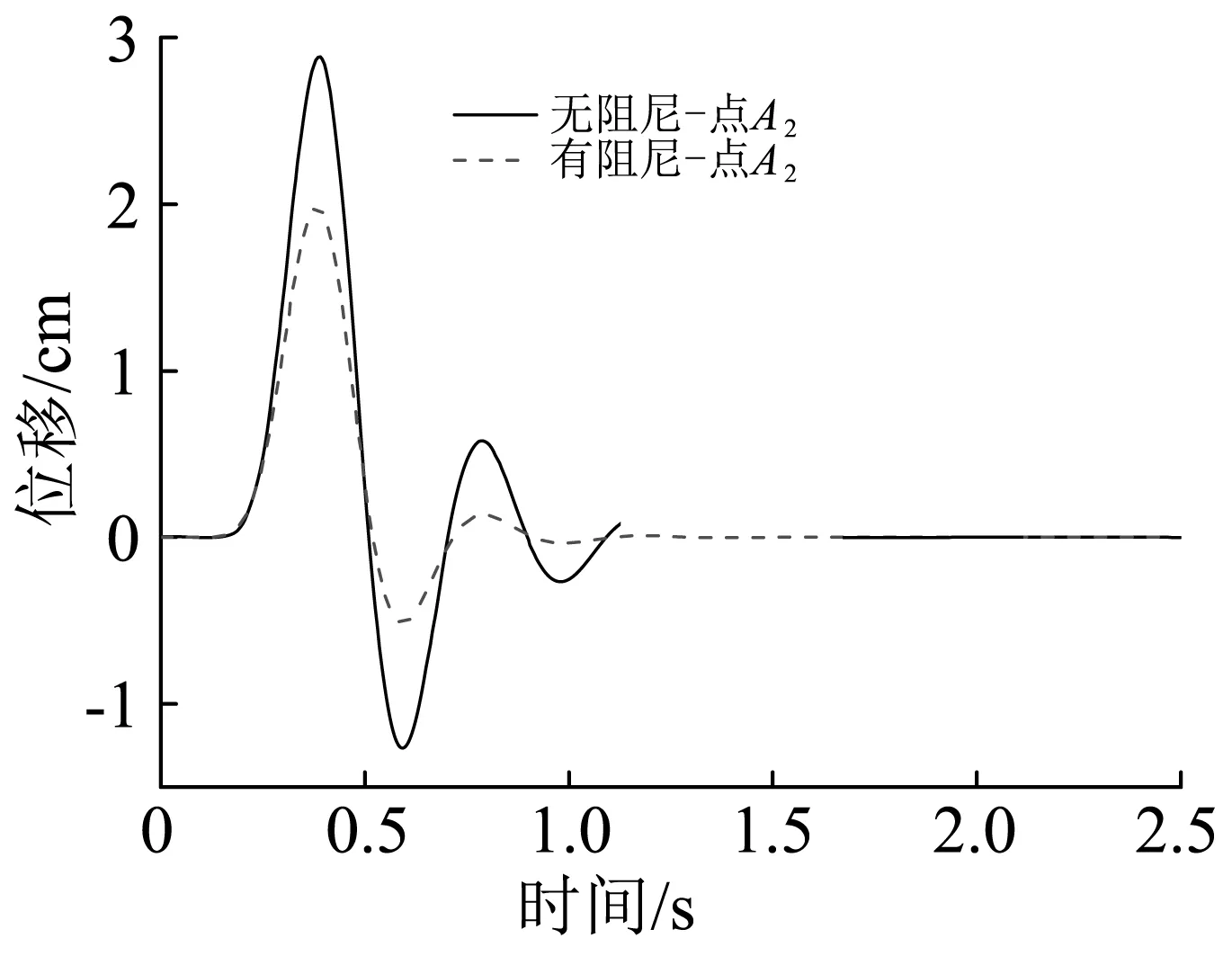
图6绘出了SH波以30°角斜入射情形下，采用一维化算法计算得到的无阻尼和有阻尼双层土模型在3个观测点处的位移响应。从图6中可以发现，有阻尼双层土模型中均匀土层和基岩层的位移时程曲线与无阻尼双层土模型的相比，两者波形一致；有阻尼与无阻尼双层土模型相比，前者在各个时刻的位移响应绝对值均减小了，尤其是在自由表面观测点A2处，位移幅值衰减幅度最大。这说明基岩与土层介质阻尼也仅影响到位移幅值，而对位移时程的波形没有影响。

根据计算结果，无阻尼与有阻尼双层土模型相比，自由表面观测点A2处的位移幅值从2.88cm减小至1.98cm，衰减幅度达31.3%；中部观测点B2的位移幅值从1.48cm减小至1.33cm，衰减幅度达10.1%；底部观测点C2的位移幅值从1.28cm衰减至1.20cm，衰减幅度达6.3%。可见，SH波斜入射下土层介质阻尼显著影响到双层土自由场的位移幅值，且其影响程度同样从底部边界向自由表面逐渐增大。

图7绘出了SH波以不同入射角入射情形下，无阻尼和有阻尼双层土在表面观测点A2处的位移幅值随入射角的变化情况。从图7中可以发现，无阻尼和有阻尼双层土的位移幅值均随着SH波入射角的增大而减小；在入射角为90°时，位移幅值减小为0，这也验证了SH波沿底部边界水平方向入射时不会在自由表面上引起位移的理论认识。此外，与无阻尼双层土模型相比，相同入射角下有阻尼双层土模型的位移幅值均减小了。计算结果表明，在SH波入射角为75°时，有阻尼双层土模型在自由表面观测点A2处的位移幅值从1.89cm(无阻尼时)减小至1.14cm，衰减幅度最大，达39.7%。从衰减幅值看，在SH波入射角为0°～45°时，有阻尼双层土模型的位移幅值皆减小了0.90cm；在SH波入射角超过45°后，位移幅值相对衰减较小。

(a) 观测点A1位移时程的计算结果

(b) 观测点B1位移时程的计算结果

(c) 观测点C1位移时程的计算结果

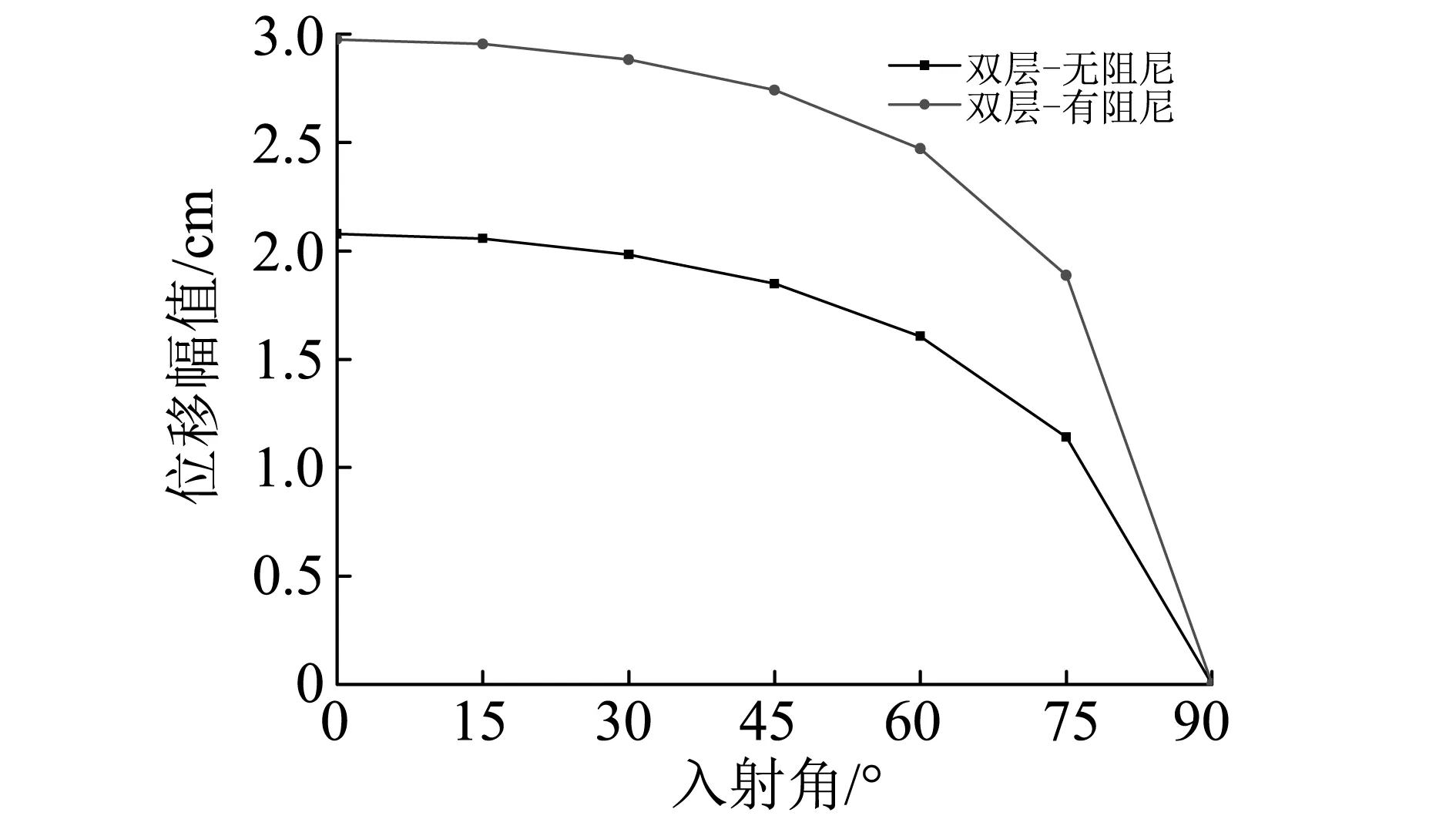
图7 观测点A2位移幅值随SH波入射角的变化曲线Fig.7 Peak displacements at joint A2by incident SH wave with different angles

4 结 论

本文基于刘晶波等的算法，提出了考虑土层介质阻尼影响的水平成层弹性介质出平面自由场的一维化时域算法，并编制了相应的数值计算程序。通过算例分析，讨论了土层介质阻尼对SH波斜入射下水平成层弹性介质出平面自由场的影响。分析结果表明：

(1)介质阻尼对水平成层弹性介质出平面的自由场有重要的影响。SH波斜入射下有阻尼与无阻尼情形相比位移幅值有明显衰减，对单层土，30°斜入射下衰减幅度可达40.5%；对双层土，最大衰减幅度可达39.7%。

(2)土层介质阻尼仅影响到SH波斜入射下自由场的位移幅值，而对位移时程的波形没有影响。

(3)不管是单层土还是双层土，与无阻尼土层相比，有阻尼土层位移幅值的衰减幅度从底部边界向自由表面逐渐增大。

[ 1 ] WOLF J P, OBERNHUBER P. Effects of horizontally traveling waves in soil-structure interaction[J]. Nuclear Engineering and Design, 1979, 57(2): 221-244.

[ 2 ] 李山有, 廖振鹏, 周正华. 大型结构地震反应数值模拟中的波动输入[J]. 地震工程与工程振动, 2001, 6(2): 1-5. LI Shanyou, LIAO Zhenpeng, ZHOU Zhenghua. Wave motion input in numerical simulation of seismic response for 1arge-scale structure[J]. Earthquake Engineering and Engineering Vibration, 2001, 6(2): 1-5.

[ 3 ] 潘旦光, 楼梦麟, 范立础. 多点输入下大跨度结构地震反应分析研究现状[J]. 同济大学学报, 2001, 29(10): 1213-1219. PAN Dan’guang, LOU Menglin, FAN Lichu. Status of seismic response analysis of long-span structures under multiple support excitations[J]. Journal of Tongji University, 2001, 29(10): 1213-1219.

[ 4 ] 杜修力, 陈维, 李亮, 等. 斜入射条件下地下结构时域地震反应分析初探[J]. 震灾防御技术, 2007, 2(3): 290-296. DU Xiuli, CHEN Wei, LI Liang, et al. Preliminary study of time-domain seismic response for underground structures to obliquely incident seismic waves[J]. Technology for Earthquake Disaster Prevention, 2007, 2(3): 290-296.

[ 5 ] 傅淑芳, 刘宝诚. 地震学教程[M]. 北京: 地震出版社, 1991.

[ 6 ] 廖振鹏. 工程波动理论导论[M]. 2版.北京: 科学出版社, 2002.

[ 7 ] HASKELL N A. The dispersion of surface waves in multi-layered media[J]. Bulletin of the Seismic Society of American, 1953, 43: 17-34.

[ 8 ] BREKHOVSHIKH L M. Waves in layered media[M]. New York: Academic Press Inc., 1980.

[ 9 ] 李山有, 王学良, 周正华. 地震波斜入射情形下水平成层半空间自由场的时域计算[J]. 吉林大学学报(地球科学版), 2003, 33(3): 372-376. LI Shanyou, WANG Xueliang, ZHOU Zhenghua. The time-step numerical simulation of free field motion of layered half-space for inclined seismic waves[J]. Journal of Jilin University(Earth Science), 2003, 33(3): 372-376.

[10] 廖振鹏, 黄孔亮, 杨柏坡, 等. 暂态波透射边界[J]. 中国科学(A辑), 1984(6): 556-564. LIAO Zhenpeng, HUANG Kongliang, YANG Baipo, et al. A transmitting boundary for transient wave[J]. Science in China(Series A) , 1984(6): 556-564.

[11] 刘晶波, 王艳. 成层半空间出平面自由波场的一维化时域算法[J]. 力学学报, 2006, 38(2): 219-225. LIU Jingbo, WANG Yan. A 1D time-domain method for 2D wave motion in elastic layered half-space by antiplane wave oblique incidence[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 219-225.

[12] 刘晶波, 王艳. 成层介质中平面内自由波场的一维化时域算法[J]. 工程力学, 2007, 24(7): 16-22. LIU Jingbo, WANG Yan. A 1D time-domain method for in-plane wave motion of free field in layered media[J]. Engineering Mechanics, 2007, 24(7): 16-22.

[13] LIU Jingbo, WANG Yan. A 1D time-domain method for inplane wave motions in a layered half-space[J]. Acta Mechanica Sinica, 2007, 23(6)：673-680.

[14] 赵密, 杜修力, 刘晶波, 等. P-SV波斜入射时成层半空间自由场的时域算法[J]. 地震工程学报, 2013, 35(1): 84-90. ZHAO Mi, DU Xiuli, LIU Jingbo, et al. Time-domain method for free field in layered half space under P-SV waves of oblique incidence[J]. China Earthquake Engineering Journal, 2013, 35(1): 84-90.

[15] 范留明, 赵钦. 成层半空间出平面自由波场的界面子波算法[J]. 地震工程学报, 2014, 36(4): 765-772. FAN Liuming, ZHAO Qin. Interfacial wavelet superposition method for out-of-plane wave motion of a free field in a layered half space[J]. China Earthquake Engineering Journal, 2014, 36(4): 765-772.

[16] 王笃国, 赵成刚. 地震波斜入射时二维成层介质自由场求解的等效线性化方法[J]. 岩土工程学报, 2016, 38(3): 554-561. WANG Duguo, ZHAO Chenggang. Two-dimensional equivalent linear seismic analysis of free field in layered half-space due to oblique incidence[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 554-561.

[17] LYSMER J, KULEMEYER R L. Finite dynamic model for infinite media[J]. Journal of Engineering Mechanics, 1969, 95(4): 859-877.

[18] WOLF P J. A comparison of time-domain transmitting boundaries[J]. Earthquake Engineering and Structure Dynamics, 1986, 14(4):655-673.

[19] DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25-42.

[20] 王振宇, 刘晶波. 成层地基非线性波动问题人工边界与波动输入研究[J]. 岩石力学与工程学报, 2004, 23(7): 1169-1173. WANG Zhenyu, LIU Jingbo. Study on wave motion input and artificial boundary for problem of nonlinear wave motion in layered soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(7): 1169-1173.

[21] 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域黏弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51. LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46-51.

[22] 刘晶波, 谷音, 杜义欣. 一致黏弹性人工边界及黏弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070-1075. LIU Jingbo, GU Yin, DU Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070-1075.

[23] 杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49-56. DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in FEA for near-field wave problem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49-56.

[24] 卢华喜, 梁平英, 尚守平. 地基非线性波动问题中黏-弹性人工边界研究[J]. 岩土力学, 2008, 29(7): 1911-1916. LU Huaxi, LIANG Pingying, SHANG Shouping. Research on viscoelastic artificial boundary for problem of nonlinear wave motion in soil[J]. Rock and Soil Mechanics, 2008, 29(7): 1911-1916.

[25] 张波, 李术才, 杨学英, 等. 三维黏弹性介质人工边界研究[J]. 岩土力学, 2009, 30(11): 3469-3475. ZHANG Bo, LI Shucai, YANG Xueying, et al. Study of three dimensional viscoelastic medium artificial boundary[J]. Rock and Soil Mechanics, 2009, 30(11): 3469-3475.

[26] 赵密, 杜修力, 刘晶波. 一种高阶精度人工边界条件：出平面外域波动问题[J]. 工程力学, 2012, 29(4): 7-14. ZHAO Mi, DU Xiuli, LIU Jingbo. A high-order accurate artificial boundary condition: out-of-plane exterior waver problem[J]. Engineering Mechanics, 2012, 29(4): 7-14.

[27] CHOPRA A K. Dynamics of structures: theory and applications to earthquake engineering [M]. 3rd ed. New Jersey: Pearson Education Inc., 2007.

A 1D time-domain method for free field motion in layered mediawith damping under obliquely incident SH wave

GAO Zhineng1, ZHUO Weidong1,2, GU Yin1,2

(1. College of Civil Engineering, Fuzhou University, Fuzhou 350116, China; 2. Key Laboratory for Multi Disaster Prevention andGovernance of Civil Engineering of Fujian Province , Fuzhou University , Fuzhou 350116, China )

The influence of obliquely incident seismic wave on the seismic responses of large and long-span structures need to be considered in seismic design. Based on a 1D time-domain method for the out-of-plane wave motion of the free field in a layered half space proposed by Liu and Wang, formulas of an explicit time-stepping method to solve the out-of-plane wave motion of the free field in layered media with damping under obliquely incident SH wave were established by using the finite difference method, and its numerical program was developed with Fortran programming language. A cases study of out-of-plane wave motions of the free field in one-layer soil and two-layer soil with damping under obliquely incident SH wave were carried out respectively. The results show that: soil damping only has effect on the peak displacements of free field motions, and has no effect on the waveforms of the displacement time histories; the displacement amplitudes in layered soil with damping reduce significantly compared with that of without damping under obliquely incident SH wave, and the displacement amplitudes can be reduced by 40.5% and 39.7% for one-layer soil and two-layer soil, respectively. The case study also indicates that the attenuation of displacement amplitudes in layered soil with damping gradually increased from the bottom boundary to the free surface.

layered media; out-of-plane wave motion; oblique incidence; 1D time-domain method; damping; time-stepping method

国家自然科学基金资助项目( 51108088)

2016-01-29 修改稿收到日期： 2016-07-01

高智能 男，博士生，1984年生

卓卫东 男，博士，教授，1966年生

TU311.3; P315.9

A

10.13465/j.cnki.jvs.2017.16.006