半转翼悬停和前进飞行升力估算方法

王孝义 张玉华 董银萍 邱 晗 陈富强 邱支振

安徽工业大学机械工程学院，马鞍山，243002

半转翼悬停和前进飞行升力估算方法

王孝义 张玉华 董银萍 邱 晗 陈富强 邱支振

安徽工业大学机械工程学院，马鞍山，243002

在分析半转翼运动模型和翼面气流特点的基础上，建立了悬停和前进两种飞行状态下的半转翼升力计算模型。根据半转翼的运动特性，推导出适合半转翼运动的升力计算解析表达式。结合半转翼样机参数，应用导出的理论公式和基于CFD软件的数值仿真模型，分别计算不同飞行条件下半转翼的升力，获得半转翼悬停和前进两种飞行状态下升力变化规律。理论计算与数值仿真所得升力曲线的对比验证了升力估算解析法的有效性和可行性。研究结果可为半转翼飞行器的参数设计与升力预估提供理论指导。

半转翼；悬停飞行；前进飞行；升力计算

0 引言

动物肢体运动形式虽各有不同，但本质上都是“不对称摆动”[1]。摆动是适应肌肉特点的运动形式，动物利用这种不对称运动产生了高效而巧妙的运动效果，像鸟类和昆虫的飞行，机动灵活，非常适合复杂环境下的活动。扑翼飞行器是模仿鸟类或昆虫飞行方式的飞行器，因其在国防和民用领域的广阔应用前景而成为各国学者研究的热点[2-5]。特别是在扑翼气动力研究方面，人们开展了理论建模[6-7]、不同工况升力试验[8-12]以及基于CFD理论的数值仿真[13-14]等一系列的研究，取得了较为丰富的成果[15]。然而，扑翼的往复快速摆动会产生较大惯性力[16-17]，导致扑翼飞行器在大型化方面遇到了难以逾越的障碍[18]。在此背景下，安徽工业大学提出了一种能避免摆动而只产生不对称运动的转动机构——半转机构[1,19]，通过对半转机构的不断改进，研制出一种简约化半转机构作为类扑翼飞行器驱动机构。这种新型飞行驱动机构具有结构简单、飞行驱动效率高、适应能力强等优点，可尝试在大尺寸、高升力上取得突破，从而使大尺寸半转翼飞行器成为可能。

在半转翼飞行器的研制中，飞行器的升力预估是最基本的环节。半转翼飞行器作为一种以转动替代摆动的新型类扑翼系统，针对其升力特性方面的研究尚未展开。本文通过分析基于简约化半转机构的半转翼运动模型和翼面气流特点，对半转翼飞行器悬停和前进两种飞行状态下的升力形成进行理论研究，旨在建立适合半转翼运动的气动力模型，探索半转翼飞行升力估算方法。

1 半转翼运动及翼面气流

1.1 半转翼运动模型

半转翼是一种适应于飞行的简约化半转机构的输出构件，也是半转翼飞行器产生升力的工作构件。如图1所示，AB为半转翼，翼展长度为2a；O1C为曲柄，半径为R。曲柄与半转翼的铰接中心C位于半转翼的中部；定点O(又称不动点)处安装转动滑块，使得定点O始终位于半转翼AB上。

图1 半转翼的平面运动模型Fig.1 Planar motion model of HRW

因以上几何约束作用，半转翼在曲柄的带动下做平面运动，即绕定点O的转动以及随铰接中心C点的平移。在定点O建立固定坐标系OXY，X轴通过曲柄转动中心O1，在动点C建立动坐标系Cxy，x轴方向沿翼的展向。设ω为曲柄的转动角速度，则半转翼转动角速度为ω/2，半转翼上任意位置D的速度为

(1)

式中,φ为曲柄的转角；x为D位置处沿翼展向的位置坐标。

令x=0，得C点的速度

vC=ωR

(2)

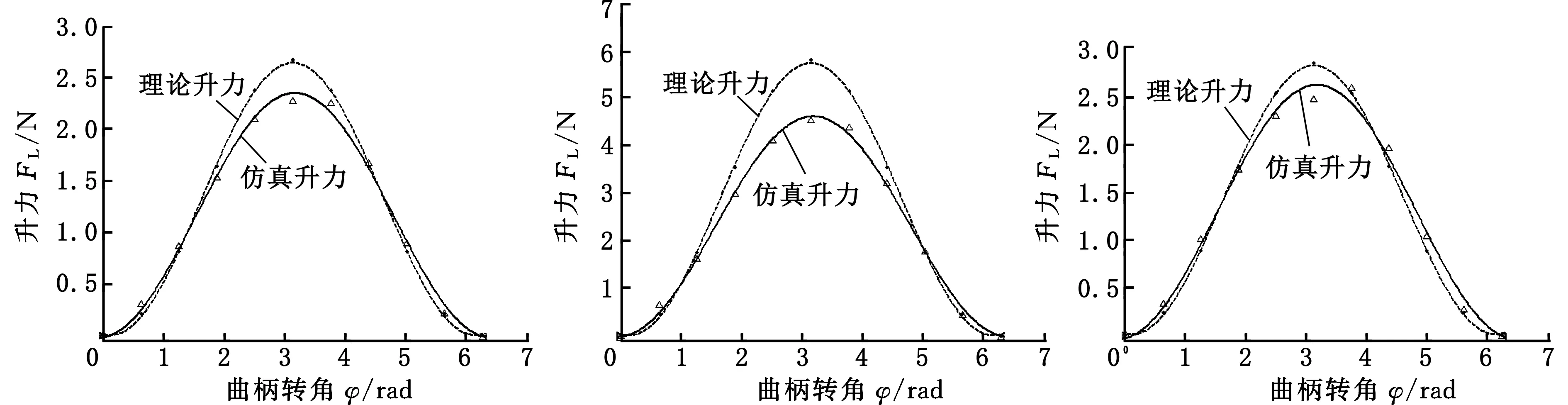
由于C点位于半转翼AB的中点，为防止B点从O点脱出， 必有a>2R。如图1所示，当半转翼逆时针转动到不动点O的左侧时，半转翼逐渐向下运动，相当于昆虫翅的下拍行程；当半转翼逆时针转动到不动点O的右侧时，半转翼逐渐向上运动，相当于昆虫翅的上挥行程。据此，可将半转翼运动区间分为下拍区和上挥区[1]。由图1可知，下拍区和上挥区区间分别为-2Rsin(φ/2)

1.2 半转翼翼面气流与迎角

半转翼飞行器有悬停和前进两种飞行状态，两种飞行状态下的翼面气流组成不同。考虑到半转翼翼片运动的周期性，对曲柄转动一周的过程进行分析。

当半转翼飞行器处于悬停飞行状态时，半转翼的运动是平面运动，因其在运转中有明显的展向伸缩运动，故翼片上会产生沿翼面展向分布的展向气流，如图2所示。考虑到除翼片两顶端的展向气流外，翼面中间的展向气流不能越过翼片，因而并不产生绕流作用，也就是说展向气流因绕流产生的升力甚小，因此，在翼面气动力元分析计算中可忽略展向气流的作用，只考虑在翼面弦向截面内的气流作用。

图2 悬停时半转翼翼面气流Fig.2 Airflow distribution on the surface of HRW in hovering flight

考虑翼面与静止空气的相对速度，气流的速度沿半转翼弦向的分布是均匀的，而沿展向的分布是变化的。半转翼上任意位置D的气流速度v可用式(1)计算，方向与vD相反，气流与半转翼的迎角α为vD与翼面切向夹角之锐角，规定下拍区α为正，上挥区α为负。由图1可得，悬停状态下气流迎角

(3)

当半转翼飞行器以速度v0前进飞行时(图3)，相当于飞行器固定而前方有-Z方向的来流，速度大小为v0，来流在半转翼上产生弦向气流。此时翼片上既有展向气流也有弦向气流，将半转翼任意点的展向气流速度分解为平行于翼面的分量vx和垂直于翼面的分量vy。如前所述,平行于翼面的展向气流分量对飞行升力的贡献甚微,可忽略不计(故图3中只给出弦向气流示意)；前方来流产生的弦向绕流可产生较大升力，此外在弦向截面内还应考虑vy对气流相对速度的影响，于是可得气流相对速度

图3 前进时半转翼翼面气流Fig.3 Airflow distribution on the surface of HRW in forward flight

(4)

vy=ω(Rsin(φ/2)+x/2)

前进状态下气流迎角用γ表示， 则由图3中v0和vy关系可得

(5)

由式(5)可见，气流迎角与作用点在弦向的位置无关，而与来流速度v0、曲柄转速ω、转角φ及作用点在展向的位置x有关。令x=0，C点在前进状态下迎角

(6)

因sin(φ/2)∈[0,1]，故C点迎角最大值

γCmax=arctan(ωR/v0)

(7)

2 半转翼悬停飞行升力估算

2.1 悬停飞行升力元

在静止空气中悬停飞行时，气流相对翼片的速度只由翼片上相应点的速度决定。沿展向的位置不同，气流的速度和迎角都是变化的，半转翼上各点处的气动力也不同。

沿展向取气动力元(图4)，dD是对应迎角α的阻流力元，它们在固定坐标系Y方向上的投影构成阻流升力元；dL是对应迎角α的绕流力元。悬停时绕流只能沿展向发生，可忽略展向气流的绕流作用，故悬停时只需计算阻流升力。由于悬停飞行时绝大多数时间处于大迎角状态，故采用平板大攻角气动力的近似计算公式[20]来估算其阻流升力。需要指出的是，半转翼在下拍区产生向上的升力，在上挥区产生向下的负“升力”。

图4 悬停时半转翼气动力元Fig.4 Aerodynamic element of HRW in hovering flight

2.2 悬停飞行的升力

悬停飞行时的升力按阻流升力计算，阻流力元计算式为

dD=0.5CD1ρhv2sin2αdx

(8)

式中，ρ为空气的密度；CD1为悬停飞行时的压差阻力系数，由实验测定。

进一步可得下拍区和上挥区的阻流升力元统一表达式：

dFLB=-dDcos(φ/2+α)

(9)

对阻流升力元沿展向在全翼进行积分，得全翼升力FLB(即悬停飞行总升力FL)：

(10)

3 半转翼前进飞行升力估算

由1.2节分析可知，前进飞行状态下半转翼飞行升力主要考虑弦向气流的影响。气流的速度和迎角沿弦向是固定不变的(不计翼边界效应)，但两者随来流速度v0、曲柄转速ω、曲柄转角φ以及作用点沿展向的位置x的变化而变化。为区分小迎角和大迎角工况，以半转翼展向对称中点C的迎角γC作为判定量。令进入小迎角区的临界迎角为γ0，则|γC|<γ0为小迎角状态，而|γC|≥γ0为大迎角状态。

3.1 半转翼前进飞行升力元

如图5所示，沿半转翼的展向截取弦向气流气动力元，气动力元的前缘为半转翼的前缘。半转翼沿展向任意微段dx受到绕流力元dL和阻流力元dD，dF代表dL和dD在垂直翼面方向分力的合力。飞行升力元dFL为dF在铅垂Y方向的分力。迎角γ规定逆时针为正，顺时针为负，由图5可知下拍区γ为正，上挥区γ为负。

图5 前进时半转翼弦向气动力元Fig.5 Aerodynamic element of chordwise HRW in forward flight

3.2 小迎角条件下弦向绕流升力

小迎角时，绕流升力由绕翼环量确定。图5中，半转翼弦向气流气动力元上的环量

(11)

任意展向长度为dx的翼元上由弦向气流产生的绕流力元

dLS=ρvΓdx=πρv2hsinγdx

(12)

进一步可得下拍区和上挥区的绕流升力元统一表达式：

(13)

对绕流升力元在全翼进行积分，可得小迎角条件下(|γC|<γ0)全翼弦向绕流升力

(14)

3.3 大迎角条件下弦向绕流升力

对半转翼大迎角条件下弦向气流产生升力的分析，仍采用平板大攻角绕流气动力的近似计算公式估算绕流升力与阻流升力。

大迎角(|γC|≥γ0)时，任意展向长度为dx的翼元上由弦向气流产生的绕流力元

dLL=0.5CD2ρv2hsinγcosγdx

(15)

其中，CD2为前进飞行时的压差阻力系数，一般也通过实验测定。需要指出的是，前进和悬停飞行条件下压差阻力系数并不相同。

进一步可得下拍区和上挥区弦向气流产生的绕流升力元统一表达式：

(16)

对绕流升力元在全翼进行积分，可得大迎角条件下全翼弦向绕流升力

(17)

3.4 半转翼前进飞行阻流升力

半转翼前进时的阻流升力主要出现在大迎角范围内。大迎角时，任意展向长度为dx的翼元上由弦向气流产生的气动阻流力元

dD=0.5CD2ρv2hsin2γdx

(18)

进一步可得下拍区和上挥区弦向气流产生的阻流升力元统一表达式：

(19)

对阻流升力元在全翼进行积分，可得大迎角条件下全翼弦向阻流升力：

(20)

3.5 前进飞行总升力

半转翼前进飞行总升力FL为弦向绕流升力FLA和弦向阻流升力FLB的合力。在一个运动周期内，FL根据迎角不同而分段计算，即

(21)

其中，FLAS、FLAL、FLB分别用式(14)、式(17)和式(20)计算。

4 半转翼升力估算方法的数值验证

为验证半转翼升力估算理论模型，根据已研制的半转翼样机(图6)模型参数，采用前述升力公式对不同飞行条件下的升力进行预估计算，并将理论计算结果与相同条件下利用XFLOW软件数值计算结果进行对比。

图6 半转翼样机(对称布置双翼片)Fig.6 HRW prototype with double symmetrical wings

4.1 升力估算实例

半转翼样机主要尺寸参数：曲柄半径R=0.06 m，翼片展向长度2a=0.282 m，弦向长度h=0.2 m。空气密度ρ=1.225 kg/m3。悬停飞行状态下压差阻力系数CD1由实验测得(其值为4.1)。前进飞行时取γ0=π/9，压差阻力系数CD2采用Dickinson等[12]通过实验修正得到的经验值3.46。设置四种悬停飞行条件(曲柄转速ω为6π rad/s，10π rad/s，20π rad/s，30π rad/s)和六种前进飞行条件(ω=20π rad/s,v0=2 m/s；ω=30π rad/s,v0=2 m/s；ω=20π rad/s,v0=3 m/s；ω=30π rad/s,v0=3 m/s；ω=20π rad/s,v0=6 m/s；ω=30π rad/s,v0=6 m/s)，分别计算上述飞行条件下曲柄运转一周内不同位置对应的半转翼悬停和前进飞行升力理论值。另外，根据半转翼样机的尺寸参数，在流体动力学仿真软件XFLOW中建立数值仿真模型，设定相关参数，分别针对以上飞行条件，对半转翼悬停和前进飞行的升力进行数值计算，获得升力仿真值。

4.2 理论计算结果与仿真结果的比较分析

图7所示为半转翼悬停飞行理论升力和仿真升力曲线比较，同时反映出不同曲柄转速下的升力变化规律。随着曲柄转速的增大，升力增大，且升力增大倍数近似等于转速增大倍数的平方。图8所示为半转翼前进飞行时的理论升力和仿真升力曲线比较，同时也反映出不同前进飞行条件下升力变化规律。来流速度相同时，升力随曲柄转速增大而增大；曲柄转速相同时，来流速度增大，升力变化却较小，说明平行于翼面的气流对半转翼升力影响不大。

(a)ω=6π rad/s

(b)ω=10π rad/s

(c)ω=20π rad/s

(d)ω=30π rad/s图7 半转翼悬停飞行理论升力和仿真升力曲线Fig.7 Lift curves of HRW in hovering flight by theoretical calculation and numerical simulation

综合图7和图8可见：①理论计算升力和仿真升力的变化趋势基本一致，两者误差小于20%，说明半转翼飞行升力的理论估算方法是有效的。②在曲柄行至中间位置，即半转翼水平下拍瞬间，半转翼飞行升力达到最大值，情况与实际相符。③悬停飞行时，半转翼升力只与曲柄转速有关；前进飞行时，半转翼升力主要取决于曲柄转速，来流速度对升力的影响比曲柄转速的影响小得多。

导致理论计算升力和仿真升力存在误差的主要原因是理论与仿真的计算条件不同，理论估算中假定翼片在理想的静止流场中运动，而仿真计算中模仿真实流场考虑了翼片对流场的扰动。因此，图7中仿真值小于理想状态的理论值，而且转速越高，翼片对流场的扰动越强烈，导致理论值与仿真值的偏差越大。另外，由于翼片的运动平面与来流方向垂直，来流会把翼片运动区域内的扰动带向下游，减少了翼片运动流场中的扰动程度，从而提高了升力数值；而且来流速度越大，带走扰动的能力越强，所以图8中当转速相同时，随着来流速度提高，仿真值与理论值的误差变小。

(a)ω=20π rad/s,v0=2 m/s (b)ω=30π rad/s,v0=2 m/s (c)ω=20π rad/s,v0=3 m/s

(d)ω=30π rad/s,v0=3 m/s (e)ω=20π rad/s,v0=6 m/s (f)ω=30π rad/s,v0=6 m/s图8 半转翼前进飞行理论升力和仿真升力曲线Fig.8 Lift curves of HRW in forward flight by theoretical calculation and numerical simulation

5 结论

(1)半转翼悬停飞行时，翼面气动力主要为由法向气流产生的阻流升力，建立了适合半转翼运动的阻流升力计算模型，导出了升力计算公式，可以估算半转翼悬停飞行状态下的升力大小。

(2)半转翼前进飞行时，升力主要来源于弦向气流。建立了适合半转翼运动的弦向流升力计算模型，根据气流迎角的不同，导出了升力计算公式，可以估算半转翼前进飞行状态下的升力大小。

(3)应用导出的表达式计算不同飞行条件下半转翼的升力，获得了半转翼悬停和前进两种飞行状态下升力变化规律。悬停飞行时，随着曲柄转速的增大，升力近似按与转速的平方成正比的规律增大；前进飞行时，半转翼升力主要取决于曲柄转速，与平行于翼面的前进速度关系不大。

(4)比较计算升力曲线与CFD数值仿真所得的升力曲线，两者变化趋势一致，最大误差小于20%。验证了升力估算解析法的有效性和可行性，可为分析半转翼飞行器的参数设计和升力预估提供重要的、便于应用的理论分析工具。

[1] 邱支振. 半转机构[M]. 合肥：中国科学技术大学出版社，2011. QIU Zhizhen.Half-rotating Mechanism [M].Hefei: Press of University of Science and Technology of China,2011.

[2] YOON S, KANG L H, JO S. Development of Air Vehicle with Active Flapping and Twisting of Wing[J]. Journal of Bionic Engineering,2011,8(1):1-9.

[3] NGUYEN Q V, CHAN W L, DEBIASI M. Hybrid Design and Performance Test of a Hovering Insect-inspired Flapping-wing Micro Aerial Vehicle[J]. Journal of Bionic Engineering, 2016,13(2):235-248.

[4] FARUQUE I A, HUMBERT J S.Wing Motion Transformation to Evaluate Aerodynamic Coupling in Flapping Wing Flight[J]. Journal of Theoretical Biology,2014,363:198-204.

[5] SMITH M. Simulating Moth Wing Aerodynamics towards the Development of Flapping Wing Technology[J]. AIAA Journal,1996,34(7):1348-1355.

[6] GURSUL I, HO C M.Oscillating Foils of High Propulsive Efficiency [J]. Journal of Fluid Mechanics,1998,360(1):41-72.

[7] TUNCER I H, WALZ R, PLATZER M. A Computational Study on the Dynamic Stall of a Flapping Airfoil [C]//16th AIAA Applied Aerodynamics Conference. Albuquerque,1998:219-225.

[8] FREYMUTH P. Thrust Generation by an Airfoil in Hover Modes [J]. Experiments in Fluids,1990,9(1/2):17-24.

[9] BRICH J M, DICKINSO M H. The Influence of Wing-wake Interactions on the Production of Aerodynamic Forces in Flapping Flight [J]. Journal of Experimental Biology, 2003,206(13):2257-2272.

[10] 刘岚，方宗德，侯宇，等. 微型扑翼飞行器的气动建模分析与试验[J].航空动力学报，2005,20(1):22-28. LIU Lan, FANG Zongde, HOU Yu, et al. Aerodynamic Modeling and Analysis of Flapping-wing MAV [J]. Journal of Aerospace Power,2005,20(1):22-28.

[11] 周骥平，朱兴龙，周建华，等.仿生扑翼飞行简化力学模型及其实验研究[J].中国机械工程，2007,18(6):631-635. ZHOU Jiping, ZHU Xinglong, ZHOU Jianhua, et al. Simple Mechanics Model and Experimental Research on Flapping-wing Based on Bionics [J]. China Mechanical Engineering, 2007,18(6):631-635.

[12] WANG Z J, BIRCH J M, DICKINSO M H. Unsteady Forces and Flows in Low Reynolds Number Hovering Flight: Two-dimensional Computations vs Robotic Wing Experiments [J]. Journal of Experimental Biology,2004,207(Pt3):449-460.

[13] 魏瑞轩，胡明朗，郭庆，等.仿鸟扑翼飞行器动力学建模[J].系统仿真学报，2009,21(15)：4811-4815. WEI Ruixuan, HU Minglang, GUO Qing, et al. Dynamics Modeling of Bird-like Flapping Wing Air Vehicle [J]. Journal of System Simulation, 2009,21(15)：4811-4815.

[14] RAMAMURTI R, SANDBERG W, LOHNER R. Simulation of Flow about Flapping Airfoils Using a Finite Element Incompressible Flow Solver [J]. AIAA Journal, 2001,39(2):253-258.

[15] 杨文青，宋笔锋，宋文萍，等.仿生微型扑翼飞行器中的空气动力学问题研究进展与挑战[J]. 实验流体力学,2015,29(3):1-10. YANG Wenqing, SONG Bifeng, SONG Wenping, et al. The Progress and Challenges of Aerodynamics in the Bionic Flapping-wing Micro Air Vehicle[J].Journal of Experiments in Fluid Mechanic,2015,29(3):1-10.

[16] 胡明朗, 魏瑞轩,崔晓峰，等. 仿昆扑翼飞行器的翅膀惯性力分析[J]. 航空动力学报,2008,23(7):1279-1286. HU Minglang, WEI Ruixuan , CUI Xiaofeng, et al. Inertia Force of Flapping Wing in Entomopter Micro Air Vehicle[J]. Journal of Aerospace Power,2008,23(7):1279-1286.

[17] COMBES S A, DANIEL T L. Into Thin Air: Contributions of Aerodynamic and Inertial-elastic Forces to Wing Bending in the Hawkmoth Manduca Sexta[J].The Journal of Experimental Biology,2003,206(17):2999-3006.

[18] DELAURIER J D. The Development and Testing of a Full-scale Ornithopter [J]. Canadian Aeronautics and Space Journal,1999,45(2):72-82.

[19] 邱晗，王孝义．半转机构——一种运动仿生机构的构成及其基本运动特性[J].机械科学与技术，2011，30 (2)：600-604. QIU Han, WANG Xiaoyi. Half-rotating Mechanism: a Biomimetic Mechanism of Animal Motion and Its Basic Motion Characteristics[J]. Mechanical Science and Technology for Aerospace Engineering,2011,30(2):600-604.

[20] 姜海波，曹树良，程忠庆．平板大攻角绕流升力和阻力系数的计算[J]．应用力学学报，2011，28(5)：518-520. JANG Haibo, CAO Shuliang, CHENG Zhongqing. Lift and Drag Coefficients of Flow around a Flat Plate at High Attack Angles [J]. Chinese Journal of Applied Mechanics,2011,28(5):518-520.

(编辑 陈 勇)

Lift Estimation of HRWs in Hovering and Forward Flights

WANG Xiaoyi ZHANG Yuhua DONG Yinping QIU Han CHEN Fuqiang QIU Zhizhen

School of Mechanical Engineering, Anhui University of Technology, Ma’anshan, Anhui,243002

The lift models of HRW in hovering and forward flights were proposed based on analyses of the motion models of HRW and flow characteristics on the surfaces of the wing. According to the motion characteristics of HRW, the analytical expressions of lift were further derived. The lifts under different flight conditions were calculated using derived formula and numerical simulation based on CFD software respectively with same HRW prototype parameters, by which the changing rule of HRW lift in hovering and forward flights could be also got. The comparisons of lift curves between the theoretical calculation and the numerical simulation demonstrated that the analytical method to estimate lift of HRW is effective and feasible. The research results mentioned above may provide important theoretical guidance for the parameter designs and lift prediction of the HRW air vehicles.

half-rotating wing(HRW); hovering flight; forward flight; lift estimation

2016-10-10

国家自然科学基金资助项目(51375014)

V212

10.3969/j.issn.1004-132X.2017.15.005

王孝义，男，1970年生。安徽工业大学机械工程学院教授、博士。主要研究方向为仿生机械、数字化设计与制造。E-mail：wangxy@ahut.edu.cn。张玉华，男，1961年生。安徽工业大学机械工程学院教授。董银萍，女，1989年生。安徽工业大学机械工程学院硕士研究生。邱 晗，男，1976年生。安徽工业大学机械工程学院实验师。陈富强，男，1960年生。安徽工业大学机械工程学院副教授。邱支振，男，1946年生。安徽工业大学机械工程学院教授。