基于BB算法的左截断威布尔分布可靠性分析

孔祥芬 张凯奇 张 俊 张 飞

1.中国民航大学航空工程学院，天津，3003002.深圳航空有限责任公司维修工程部，深圳，518000

基于BB算法的左截断威布尔分布可靠性分析

孔祥芬1张凯奇1张 俊2张 飞2

1.中国民航大学航空工程学院，天津，3003002.深圳航空有限责任公司维修工程部，深圳，518000

针对寿命分布类型和参数估计方法问题，对国内某航空公司现役机型B737-800飞机主起落架减振支柱漏油故障数据进行可靠性分析。结合数据类型特点，初步预判其寿命分布类型可能为左截断两参数威布尔分布、对数正态分布、指数分布。基于极大似然估计法分别估计三种分布的未知参数，并利用根据BB算法改进的柯尔莫哥洛夫-斯米尔诺夫假设检验(K-S检验)法判断其寿命分布类型。实证分析结果表明，采用左截断两参数威布尔分布来拟合是合适的，并提出了具体维修建议。

起落架；可靠性分析；极大似然估计；K-S检验；左截断威布尔分布；BB算法

0 引言

飞机起落架减振支柱是飞机安全飞行的重要前提和基础[1]，其工作的可靠性直接影响到飞机起飞和着陆性能的实现及飞行安全[2]。针对各飞机系统或部件的不同故障模式和故障后果，拟定不同的维修方式和维修制度，对提高飞行安全和控制维修成本具有重要意义[3]。目前，学者们对飞机部件的可靠性分析问题已进行了大量的研究。在失效数据分布类型研究方面，周英彪等[4]对比分析了两参数威布尔分布与三参数威布尔分布的优点和缺点，并应用球磨机缺陷数据进行了实证分析。在失效数据精度分析上，辛龙等[5]以最小二乘法为威布尔分布参数估计方法，从经验分布函数角度对比了平均秩次法和中位秩法，并证明平均秩次法精度更高。伍建军等[6]进一步结合平均秩次法和加权最小二乘法的优点，对两参数威布尔分布进行了参数估计，对比了水平残差平方和垂直残差平方，得到形状参数取值范围不同应该采取不同的参数估计方法的结论。秦明等[7]发现，威布尔分布参数的最小二乘估计并不是最优方法，并且指出极大似然估计法(maximum likelihood estimation,MLE)对于较复杂样本情况仍然具有优良的适用性和精确的估计。吴江[8]应用粒子群算法(particle swarm optimization,PSO)对混合威布尔分布的参数估计值进行了数值逼近，对比证明了该方法收敛速度相对较快，不易陷入局部最优解，但该方法并没有考虑K-S法拟合检验中参考统计量D的选取问题，仅对参数值的数值逼近方法进行了优化。

研究和实践结果表明，机械、电气、气动、液压本身或其所包含零件和子系统的故障模式适合用威布尔分布来拟合[9]。在参数估计的数值分析方法中，MLE方法不仅可以得到理想的参数估计结果，而且适用于完全样本以外的截尾数据和截断数据情形，甚至对于小样本情形也有较好的适用性。国内某航空公司自2010年9月以来，引进了大量B737-800飞机，其数量约占公司机队规模的一半左右。然而该机型飞机主起落架减振支柱渗油故障时有发生。截止到2016年3月底，在统计到的35架B737-800飞机起落架系统故障记录中共发生70多次主起落架减振支柱漏油故障。因而从安全角度以及经济效益影响方面综合考量，对B737-800飞机主起落架减振支柱漏油故障的寿命分布及其失效原因加以分析和研究是非常必要和有现实意义的。

本文以该航空公司35架B737-800飞机主起落架油气式减振支柱漏油故障数据(平均无故障间隔时间)为研究对象进行寿命分布对比研究，以极大似然估计法为核心进行参数估计，并对参数估计结果进行了基于BB算法改进的K-S拟合检验。基于所获得的寿命分布结果，进一步开展主起落架减振支柱漏油故障数据可靠性分析，并提出了相应的维护措施。

1 相关理论

1.1 左截断两参数威布尔分布

两参数威布尔分布的概率分布函数[10]如下：

(1)

其中，τ为随机变量；非负参数α为尺度参数；β为形状参数。形状参数β取值不同，概率密度曲线的形状不同，恰好能拟合浴盆形状的寿命分布曲线的不同时期。如果假定设备的寿命符合两参数威布尔分布，则可以通过形状参数β的不同值来建议维修方式[11]。

如果一个样本容量为n的独立同分布左截断数据集合(τ1，τ2，…τn)具有τL<τi(i=1,2,…,n)的性质，其中τL为非负参数，表示数据的左截断点，则左截断威布尔分布的概率分布函数和密度函数分别为

(2)

(3)

τ>τL

本文假设非负参数左截断点τL是已知或可以设定的，则利用极大似然估计法可以得到确定分布参数α、β似然估计值的方程：

(4)

(5)

(6)

如果不满足式(6)要求，则会求出无效解α=β=0。

1.2 左截断两参威布尔分布的Kolmogorov-Smirnov检验

单样本的Kolmogorov-Smirnov检验(K-S检验)用来检验一组样本数据的观测经验分布是否与某一已知的理论分布相符合，当两者的差距很小时，推断该样本取自已知的理论分布。

(7)

根据Brownian Bridge和Donsker’s定理以及数值分析法(Brownian Bridge-Donsker’s， BB)[12-14]，可以得到临界值DL的数值方法逼近值。限于篇幅，仅给出相应理论推导结论(以下结论公式均假定显著性水平取值为0.05)。

当参数α、β已知时，临界值DL可看作关于样本容量n的函数：

(8)

(9)

η≡(τL/α)β

其中，η为截断参数。当把DL当作关于截断参数η的函数时，有

(10)

其中，A(n)、B(n)、C(n)、D(n)、E(n)均为BB算法给出的式(10)中涉及的具体参数值。结合式(8)和式(10)，可以得到修正的临界值DL函数形式：

(11)

表1给出了显著水平为0.05时参数A、B、C、D、E、F的取值。

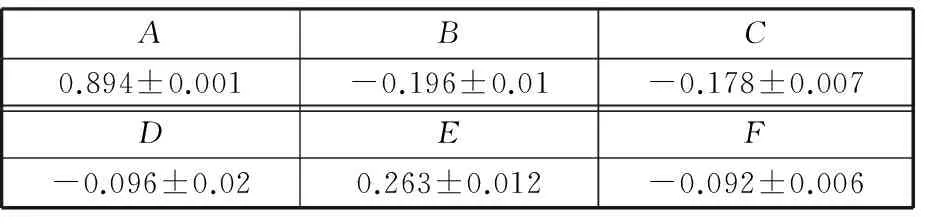
表1 威布尔分布BB算法K-S检验拟合参数对照表

2 主起落架减振支柱漏油故障数据寿命分布

2.1 故障数据的采集与处理

本文采集到的原始故障数据来自国内某航空公司35架B737-800飞机起落架系统的电子版故障记录，记录时间从2010年9月14日到2016年3月29日。本文考虑的B737-800飞机主起落架减振支柱漏油故障数据主要包括以下两种类型：①在故障描述中说明主起落架减振支柱漏油严重，并在排故措施中采取更换封严等措施的故障；②在故障描述中体现主起落架减振支柱发生漏油现象，并因后续漏油决定采取持续监控或镜面加热措施，且在排故措施中不符合勤务范围而采取更换封严等措施的故障。

利用单机同一主起落架减振支柱相邻两次漏油故障的飞行小时数(NF)记录，得到其可靠性计算指标故障间隔时间，并按照故障间隔时间从小到大升序排列，具体统计见表2。

对表2的故障间隔时间以NF=800为间隔进行分组，绘制频数分布直方图(图1)。

频数分布直方图可以直观地体现数据的趋中性和分散性，可预测数据的分布类型。观察图1的数据分布趋势，初步预测B737-800飞机主起落架减振支柱漏油故障数据分布符合指数分布、对数正态分布和左截断两参数威布尔分布，且由数据走势预判左截断两参数威布尔分布的形状参数β>1。

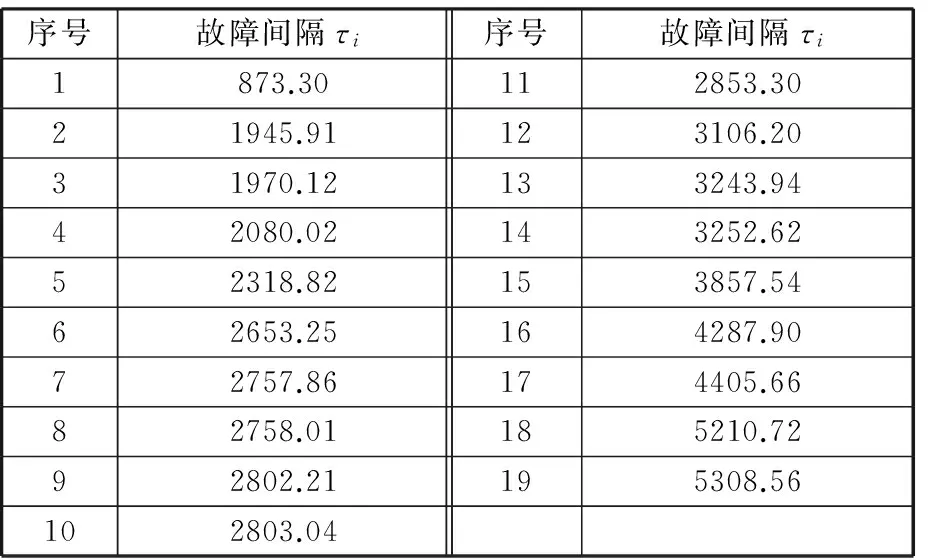
表2 B737-800飞机主起落架减振支柱漏油故障间隔时间统计表

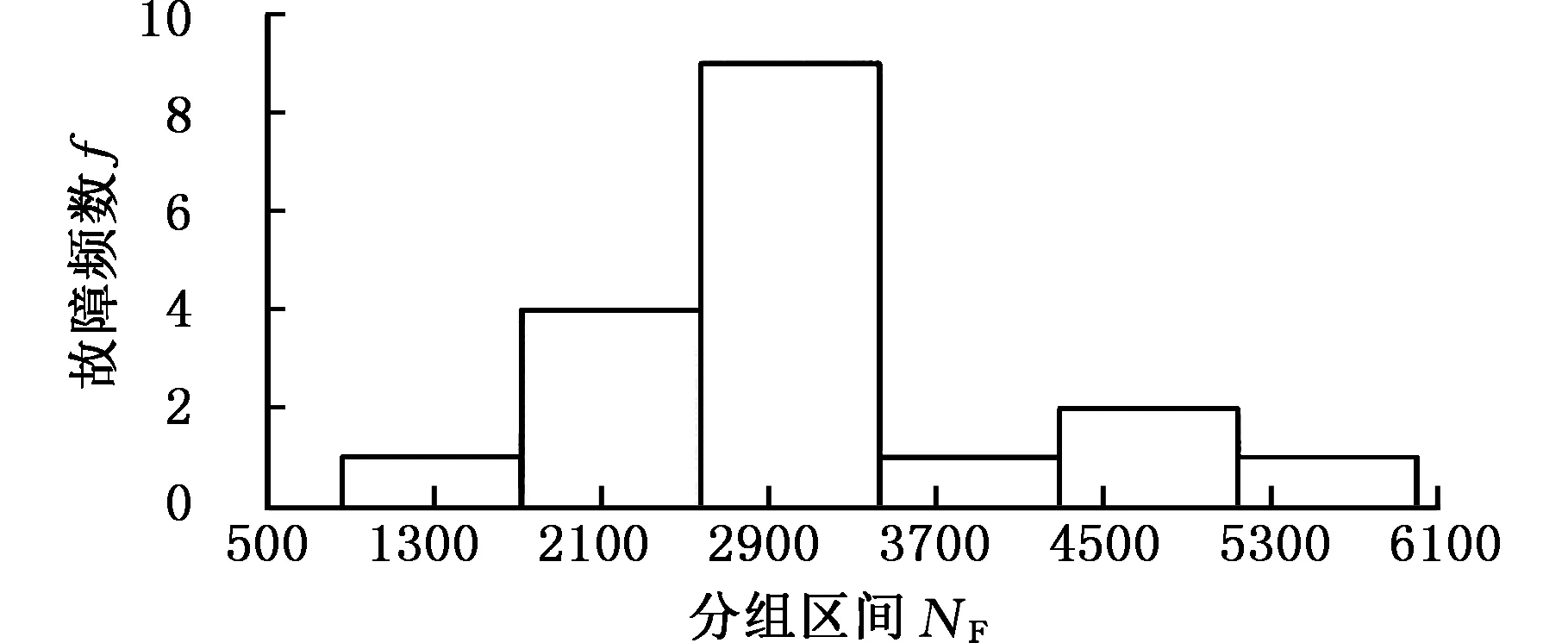
图1 B737-800飞机主起落减振支柱漏油故障频数分布直方图Fig.1 Frequency distribution histogram of main landing gear shock absorber pillar oil spill for B737-800

2.2 寿命分布类型的参数估计与检验

2.2.1 参数估计与检验步骤

基于极大似然估计法，利用MATLAB软件编程计算估计分布函数对应未知参数。具体参数为：指数分布的参数λ、对数正态分布的对数均值μ和对数标准差σ，左截断两参数威布尔分布的尺度参数α和形状参数β。运用K-S检验法对各分布函数进行拟合优度检验，比较各个统计观察值Dn，若Dn相差较大，则Dn较小的分布拟合效果比较好，更符合实际情况；若Dn相差不大，则进一步利用Minitab软件进行Personχ2拟合优度交叉检验。计算出相关系数ρxy并绘制相应的概率图，最终验证数据的分布类型。

2.2.2 参数估计与检验实例过程

首先对提供的B737-800飞机主起落架减振支柱漏油故障数据进行过滤，剔除无用数据。由于本文主要侧重对左截断类型数据的研究，故将截尾数据等同于无用数据处理。得到截断水平p≈0.3，并根据式(9)计算得到相应的截断参数η≈0.35。则取定n=19、η=0.35的情况下，结合表1参数值代入式(11)，得到DL(0.35,19)≈0.9525。

运用MATLAB编程，计算得到B737-800飞机主起落架减振支柱漏油故障数据威布尔分布参数的估计值α=3445.7，β=3.0，再结合式(9)计算得到截断点τL≈2428.29。则B737-800飞机主起落架减振支柱漏油故障的寿命分布函数

(12)

由表2数据和式(7)，计算得到Dn=0.1681。显然Dn≈0.2185，所以接受原假设，即该故障数据分布符合左截断两参数威布尔分布。

2.2.3 参数估计与检验结果对比分析

同理，利用MATLAB编程分别计算另外两种分布的参数，然后按K-S检验步骤进行拟合检验。三种分布的对比结果列于表3。

表3 B737-800飞机主起落架减振支柱漏油故障寿命分布参数估计及K-S检验

由表3可见，B737-800飞机主起落架减振支柱漏油故障间隔时间符合左截断两参数威布尔分布和对数正态分布，并且拟合效果相近，两参数威布尔分布拟合效果相对更好。进一步利用Minitab软件对对数正态分布和左截断两参数威布尔分布进行Personχ2拟合优度检验，拟合结果如图2所示。

(a)对数正态分布 (b)威布尔分布 (95%置信区间) (95%置信区间)图2 对数正态分布、威布尔分布拟合优度检验Fig.2 Goodness of fit test of lognormal distribution and Weibull distribution

图2表明，两种检验对应的P值均大于显著性0.05，表明两种分布假设均成立，但对B737-800飞机主起落架减振支柱漏油故障数据拟合效果较好的为左截断两参数威布尔分布。此时运用MATLAB程序求得其相关系数ρxy=0.9654，弃真概率小于0.05，有理由相信用左截断两参数威布尔分布拟合B737-800飞机主起落架减振支柱漏油故障的寿命分布更好。运用MATLAB程序绘制其威布尔概率图，如图3所示。

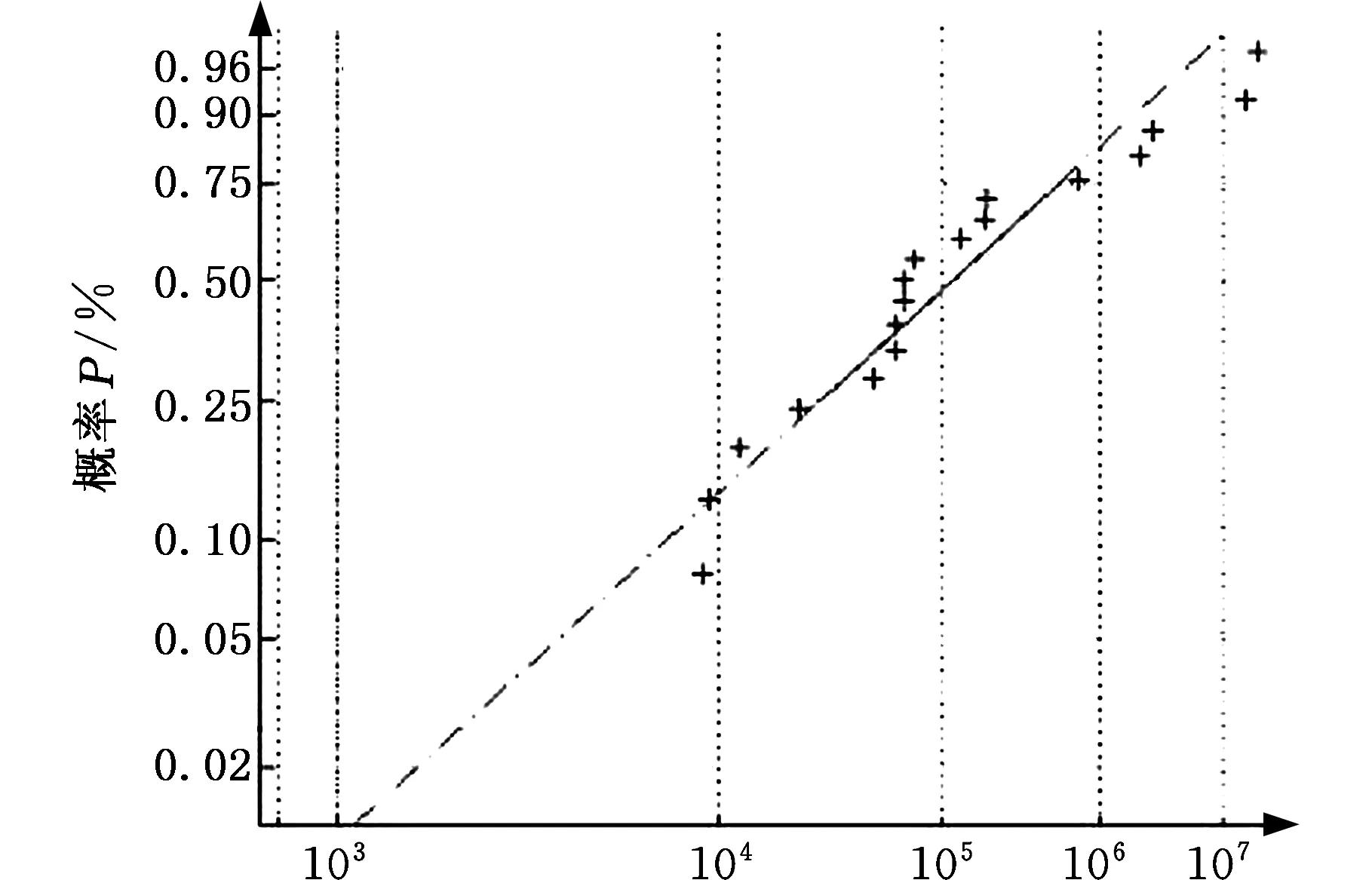
图3 威布尔概率图 Fig.3 Weibull Probability Chart

图3中，数据点(xi,yi)是均匀且趋向于一条直线分布的，这也充分说明B737-800飞机主起落架减振支柱漏油故障的寿命分布用左截断两参数威布尔分布来拟合是准确的。

3 主起落架减振支柱漏油故障数据可靠性分析

B737-800飞机主起落架减振支柱漏油故障较好寿命分布为左截断两参数威布尔分布，其中，β=3.0，1<β<4，其失效率随时间的延长而增大，故障类型为早期损耗，可以通过优化相应的预定维修计划来提高可靠性。具体可以采用硬时限的控制方式，即确定一个由合理的可靠度计算出的使用时限，当使用时间达到该时限时进行维护或翻修。

应用MATLAB软件分别绘出B737-800飞机主起落架减振支柱漏油故障左截断两参数威布尔分布(α=3445.7，β=3)的失效率函数曲线和可靠度函数曲线，如图4、图5所示。

图4 失效率函数曲线Fig.4 Failure rate function curve

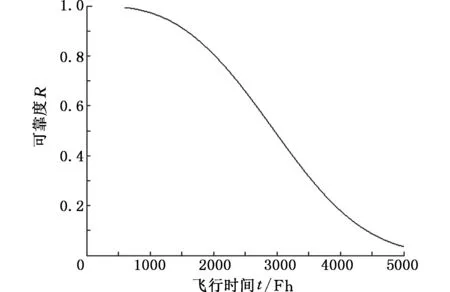
图5 可靠度函数曲线Fig.5 Reliability function curve

由失效率函数曲线可知，B737-800飞机主起落架减振支柱漏油故障大约在NF=1500时失效率明显上升，同时由可靠度函数曲线可知其可靠度在NF=1500左右急剧下降。假设该减振支柱已工作NF=1500，则当前的失效率λ(1500)=1.65×10-4/Fh，可靠度R(1500)=0.92，这表明B737-800飞机主起落架减振支柱在工作时间达NF=1500后，单位时间内的失效率为1.65×10-4，也表明每10个这样的减振支柱在工作时间达NF=1000后就有约1～2个产生漏油故障。假设可靠性维修大纲要求B737-800飞机主起落架减振支柱可靠度为92%才能正常工作，则该作动器工作时间大约在NF=1500左右就必须进行检修，这显然符合工程实际中起落架部件的可靠度往往大于90%的要求。

经计算得到B737-800飞机主起落架减振支柱在NF=500时R(500)=0.9969；在NF=800时R(800)=0.9876；在NF=1000时R(1000)=0.9759；在NF=1200时R(1200)=0.9586。假设工程实际中要求起落架部件的可靠度为99%以上，则建议在NF=500以后就应密切关注其实际运行状态。此外，状态检修方面，如点检管理等，需要给出适当的状态检测时间间隔，即需要计算出平均无故障工作时间tMBF。通常情况下，状态检测周期Tm=0.10tMBF，此处给出根据威布尔分布两参数计算得到的tMBF计算公式：

tMBF=ηΓ(1+1/β)

(13)

代入数据α=3445.7，β=3，得tMBF=3077.01，则状态检测周期Tm=307.70。因此，建议每隔NF=308左右，对主起落架减振支柱进行漏油方面的状态检测。

4 结语

工程实际中要求起落架部件的可靠度为99%以上，建议在NF=500以后就应密切关注其实际运行状态。在点检方面，建议每隔NF=308左右，对主起落架减振支柱进行漏油方面的状态检测。同时航空公司的航材部门可以根据本文结论预测需要储备航材的种类和数量，为进行合理备件提供决策依据，进而节约公司维修成本，提高飞机的使用效率。研究结果可为飞机其他系统、子系统及其部件的寿命分布研究和可靠性分析提供参考。

[1] 王红，凌云，何超．对172R型飞机前起落架减振支柱渗油故障诊断及解决方法的研究[J].机床与液压，2016，44(4):142-144． WANG Hong, LING Yun, HE Chao. The Study of the Leakage Fault Diagnosis and Solution of 172R Front Landing Gear Shock Strut Oil[J]. Machine Tool & Hydraulics,2016,44(4):142-144．

[2] LU Lixian, LEI Jianhe. Design and Reliability Prediction of a Distributed Landing Gear Control System [J].Aircraft Engineering and Aerospace Technology, 2010,82(1):15-22.

[3] 孙见忠,左洪福,梁坤. 基于民航发动机状态数据的涡轮叶片剩余寿命评估[J]. 机械工程学报,2015,51(23):53-59. SUN Jianzhong, ZUO Hongfu, LIANG Kun. Remaining Useful Life Estimation Method for the Turbine Blade of a Civil Aircraft Engine Based on the QAR and Field Failure Data[J]. Journal of Mechanical Engineering, 2015,51(23):53-59.

[4] 周英彪,段权鹏,范杜平. 利用威布尔分布模型对球磨机可靠性分析[J]. 热能动力工程,2009,24(1):95-99. ZHOU Yingbiao, DUAN Quanpeng, FAN Duping. The Reliability Analysis of Ball Mill by Weibull Distribution Model[J].Journal of Engineering for Thermal Energy and Power, 2009,24(1):95-99.

[5] 辛龙,周越文,翟颖烨,等. 基于Weibull分布的航空装备部件寿命预测研究[J].电光与控制,2014,21(12):102-105. XIN Long, ZHOU Yuewen, ZHAI Yingye, et al. Weibull Distribution Based Lifetime Prediction for Components of Aerial Equipments[J]. Electronics Optics & Control, 2014,21(12):102-105.

[6] 伍建军,游雄雄,吴事浪,等.典型矿冶废旧零部件剩余寿命预测模型与可再制造性评估决策方法[J]. 机械科学与技术,2014,33(12):1859-1864. WU Jianjun, YOU Xiongxiong, WU Shilang, et al. Remanufacturing Assessment of Typical Mining Waste Parts Based on Remaining Life Prediction Model[J]. Mechanical Science and Technology for Aerospace Engineering, 2014,33(12):1859-1864.

[7] 秦明,巫世晶,彭潇, 等. 一种服从威布尔分布装备的可靠性评估方法[J]. 武汉大学学报(工学版),2008,41(6):100-102. QIN Ming, WU Shijing, PENG Xiao, et al. A Reliability Evaluation Method for Equipment with a Weibull Failure Distribution[J]. Engineering Journal of Wuhan University,2008,41(6):100-102.

[8] 吴江.飞机可靠性分析中的混合威布尔分布参数估计方法[J]. 工程设计学报,2015,22(1):26-29. WU Jiang. Parameter Estimation Method of Mixed Weibull Distribution in Reliability Analysis of Aircraft[J]. Chinese Journal of Engineering Design, 2015,22(1):26-29.

[9] LI S M, DONG C L, HUANG Y X.Evaluate Reliableness of Aero-engine Turbine Blades Based on Weibull-distributing [J]. Journal of Civil Aviation University of China, 2008,26(4):14-17.

[10] BLOCKJ B. A Study of Aviation Field Data Fitting to a Two Parameter Weibull Distribution [C]//Risk, Reliability and Societal Safety: Proceedings of the European Safety and Reliability Conference 2007. Stavanger,2007:1339-1445.

[11] 徐微,胡伟明,孙鹏. 基于两参数威布尔分布的设备可靠性预测研究[J]. 中国工程机械学报,2013,11(2):112-116. XU Wei, HU Weiming, SUN Peng. Equipment Reliability Prediction Based on Dual-parametric Weibull Distribution [J].Chinese Journal of Construction Machinery, 2013,11(2):112-116.

[12] PANC C, CHU L. Reliability Assessment for One-shot Product with Weibull Lifetime Components[J]. International Journal of Quality & Reliability Management,2010,27(5):596-610.

[13] KIZILERSU A, KREER M, THOMAS A W. Goodness-of-fit Testing for Left-truncated Two-parameter Weibull Distributions with Known Truncation Point[J]. Austrian Journal of Statistics,2016,45(3):15-42.

[14] O’Connor P T.Practical Reliability Engineering [M]. 4th ed. London:Heyden & Son Ltd.,2002.

(编辑 陈 勇)

Reliability Analysis of Left-truncated Weibull Distribution Modified by BB Algorithm

KONG Xiangfen1ZHANG Kaiqi1ZHANG Jun2ZHANG Fei2

1.College of Aeronautical Engineering, Cival Aviation University of China, Tianjin，300300 2.Maintenance & Engineering Department of Shenzhen Airlines, Shenzhen, Guangdong，518000

A reliability analysis was done based on the failure data of B737-800 main landing gear shock strut oil leakages herein, which came from a domestic airlines’ electronic records, in consideration of the life distribution type and parameter estimation method. The characteristics of data preliminarily demonstrated that the life distribution type might be left-truncated two parameter Weibull distribution, logarithmic normal distribution or exponential distribution. Next, the parameters corresponding to three types of distributions were estimated by using the MLE method. Then, the Kolmogorov-Smirnov(K-S) hypothesis test, which modified by BB algorithm and goodness-of-fit test , was used to identify and confirm the life distribution function model. The analysis results show that the distribution of the data is left-truncated two parameter Weibull distribution. In the end, reasonable maintenance plan and optimized maintenance scheme are provided.

landing gear；reliability analysis；maximum likelihood estimation(MLE)；Kolmogorov-Smirnov (K-S)hypothesis testing；left-truncated Weibull distribution；BB(Brownian Bridge-Donsker’s)algorithm

2016-10-11

航空科学基金资助项目(20130267001)

V226.3

10.3969/j.issn.1004-132X.2017.15.012

孔祥芬，女，1974年生。中国民航大学航空工程学院副教授。主要研究方向为工业工程、质量管理与服务质量。E-mail:759185381@qq.com。张凯奇，男，1989年生。中国民航大学航空工程学院硕士研究生。张 俊，男，1993年生。深圳航空有限责任公司维修工程部航线维护工程师。张 飞，男，1989年生。深圳航空有限责任公司维修工程部航线维护助理工程师。