欠驱动弹跳机器人最优运动姿态的驱动器配置

孟祥艳 葛文杰

西北工业大学机电学院，西安,710072

欠驱动弹跳机器人最优运动姿态的驱动器配置

孟祥艳 葛文杰

西北工业大学机电学院，西安,710072

研究了具有一个被动关节的三关节单腿欠驱动弹跳机器人的轨迹规划问题。首先建立欠驱动机器人在着地阶段的动力学模型;然后采用数值迭代的方法，以主动关节驱动力矩最小为优化目标，得出了机器人各关节转角的运动规律;最后通过仿真得到三种驱动器配置情况下机器人的关节转角运动规律、姿态图以及驱动力矩，并对其进行了分析比较。结果表明：所提出的运动规划方法是可行的，采用髋关节和踝关节驱动是三种驱动器配置中最合理的情况。

弹跳机器人；轨迹规划；欠驱动；着地阶段

0 引言

随着机器人应用范围的扩大，机器人面临的工作环境越来越复杂，这就要求机器人具有较高的运动灵活性和自主能力。弹跳机器人[1-4]可以越过障碍物和沟渠，对地形有较强的适应能力，所以弹跳机器人具有广阔的应用前景。欠驱动机器人具有运动灵活、质量小、成本低和能耗低等优点，已成为当今机器人研究的热点。但欠驱动跳跃机器人的被动关节受到二阶非完整约束(即加速度约束)，使得机器人的运动规划变得非常困难，至今还没有成熟的理论来解决欠驱动机器人的运动规划问题。

针对欠驱动机械臂，BERGERMAN等[5]通过控制关节制动器的开关状态，得到一系列连接起始和目标位形的轨迹，实现了机器人的无碰撞运动规划。YOSHIKAWA等[6]针对平面三自由度欠驱动系统，使轨迹能从任意给定初始点出发，中途经过任意给定点，收敛到任意期望点。LYNCH等[7]把轨迹规划问题分解成简单的问题，采用时间尺度方法实现了平面三自由度机械臂的无碰撞路径规划。LUCA等[8]采用动力学反馈来处理线性化末端为欠驱动杆的平面三自由度欠驱动机械臂的运动规划问题。NISHIDA等[9]把轨迹规划变换成约束问题，采用多层感知器构成的神经网络实现了平面二自由度机器人的轨迹规划。GREGORY等[10]实现了欠驱动平面机械臂的能量最优运动规划。在国内，何广平等[11]把人工势场法引入冗余度机械臂的避障运动规划，提出了欠驱动冗余度机械臂的虚拟模型控制方法。陈伟[12]通过控制被动关节的加速度，产生不同形式的平动、转动和平面运动，将这些运动进行组合，实现了机械臂的运动规划。刘庆波[13]采用遗传算法实现了欠驱动机器人的最优运动规划和避障运动规划。WU等[14]考虑具有欠驱动相的弹跳机器人的轨迹规划问题，用规划Bezier曲线表示主动关节的轨迹，基于驱动能量最小目标进行轨迹规划。刘载淳[15]通过推导欠驱动跳跃机器人的伪逆运动学方程，采用模型降阶的方法，对四刚体欠驱动跳跃机器人进行了运动规划研究。HE等[16]用多项式函数描述关节运动规律来研究四刚体弹性欠驱动弹跳机器人的最优运动规划问题。

由于欠驱动机器人具备多种优势、并拥有很好的应用前景，故本文针对具有髋关节、踝关节及趾关节的三关节单腿欠驱动跳跃机器人轨迹规划问题，研究具有两个主动关节的欠驱动三关节弹跳机器人的最佳驱动器配置方案。首先建立欠驱动弹跳机器人着地阶段的动力学模型；然后采用数值递推和优化的方法实现了机器人的关节空间运动规划；最后对不同驱动器配置下弹跳机器人的起跳姿态等进行了比较。

1 机器人建模

如图1所示，弹跳机器人由身体1、腿2、脚3和脚趾4组成，假设机器人在着地阶段不产生反弹、打滑，脚趾与地面始终保持接触。取地面为参考系，建立以趾关节C为原点的固定参考坐标系Cxy。

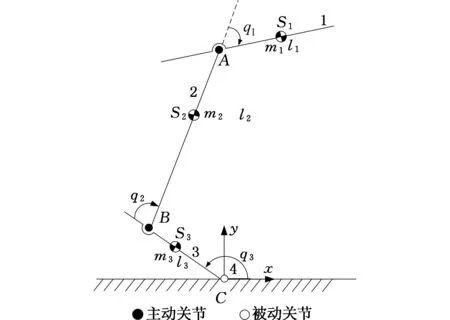
图1 弹跳机器人模型Fig.1 Model of hopping robot

设机器人各杆件的长度为li(i=1,2,3)，各杆的相对位置转角为qi(逆时针方向为正)，各杆的质量为mi，质心位置为lSi，各杆绕质心的转动惯量为Ji，关节A、B、C处驱动力矩分别为τ1、τ2、τ3。

选取q=[q1q2q3]T作为系统的广义坐标，根据拉格朗日方程，建立机器人在着地阶段的动力学方程：

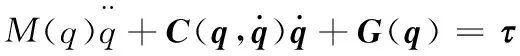
(1)

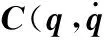
本文研究包含2个主动关节和1个被动关节的欠驱动弹跳机器人，根据驱动器配置的不同，共分为以下三种情况。

(1)髋关节和踝关节为主动关节，趾关节为被动关节，τ= [τ1τ20]T。

(2)髋关节和趾关节为主动关节，踝关节为被动关节，τ = [τ10 τ3]T。

(3)踝关节和趾关节为主动关节，髋关节为被动关节，τ= [0τ2τ3]T。

根据各关节是否存在驱动，可将式(1)写成主动和被动关节分离的形式：

(2)

(3)

式中，qa、qp分别为主动关节和被动关节的角位移；τa为主动关节的驱动力矩。

矩阵Mpp为正定矩阵，它的逆是存在的。解式(3)，得到主动和被动关节之间的耦合关系:

(4)

对机器人进行运动学分析，求得机器人总质心的位置矢量:

X=f(q)

(5)

式中，X为机器人总质心在x和y方向上的分量，X=[xCyC]。

对式(5)求二阶导数，得机器人总质心的加速度矢量：

(6)

式中，J为机器人的雅可比矩阵，J=[JaJp]。

将主被动关节的耦合关系式(4)代入质心加速度方程中，消去总质心加速度方程中被动关节的加速度，得

(7)

式(7)可简写作

(8)

式(8)可视为总质心加速度与主动关节加速度的耦合关系式。

2 关节运动规划

机器人关节空间运动规划的目标：给定机器人在着地阶段的总质心位置轨迹，规划机器人在关节空间的各关节转角运动规律。

机器人的逆运动学问题是一个复杂的非线性问题，通常不存在解析解，且解的存在具有多解性；同时，欠驱动机器人由于被动关节的存在，故主动关节和被动关节之间还必须满足耦合关系，由此，本文采用数值方法求解机器人关节空间运动规划问题。

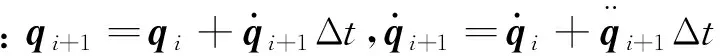
首先根据机器人起跳时应满足的约束条件，采用五次多项式规划得到机器人总质心运动规律。其次根据质心初始位置和速度反求运动学方程，得到各关节转角和速度的初值，将机器人的关节转角和速度值代入耦合方程式(8)，则式(8)变成一个关于机器人主动关节加速度的线性方程,将其作为优化时的约束条件。再次以主动关节驱动力矩最小为优化目标，建立机器人着地阶段关节空间运动规划的目标函数：

(9)

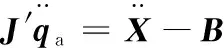
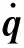
3 不同驱动形式下的运动规划比较

采用前述方法，分别对采用不同驱动器配置时的弹跳机器人进行运动规划，规划时采用的机器人参数、质心运动轨迹和初始条件等保持不变。

在仿真计算中，取机器人起跳阶段时间t=0.15 s,离散时间间隔Δt=0.002 s，采用MATLAB对该欠驱动机器人进行运动规划仿真，其中跳跃机器人参数[2]见表1。

表1 物理参数

分析采用不同驱动器配置时进行起跳过程轨迹规划所得到的关节运动规律、起跳姿态图和主动关节力矩变化规律。

从图2所示的轨迹规划得到三种情况下的各关节转角变化规律，可以看出：①对运动时间进行对比，其中t=0.15 s是机器人的起跳离地时刻，只有趾关节被动时机器人的运动才能达到起跳离地时刻，另外两种情况中合理的运动时间都比较短，无法达到起跳时的加速度和速度；②图2b中各关节运动规律在前期和图2a大致相同，但踝关节和趾关节的转角在0.07 s后急剧变化，使得机器人运动情况变差；图2c中踝关节的运动规律比较合理，但趾关节的转角先减小后增大，然后迅速减小，表明机器人先向前运动再向后倒，这两种情况都是不符合生物运动规律的。

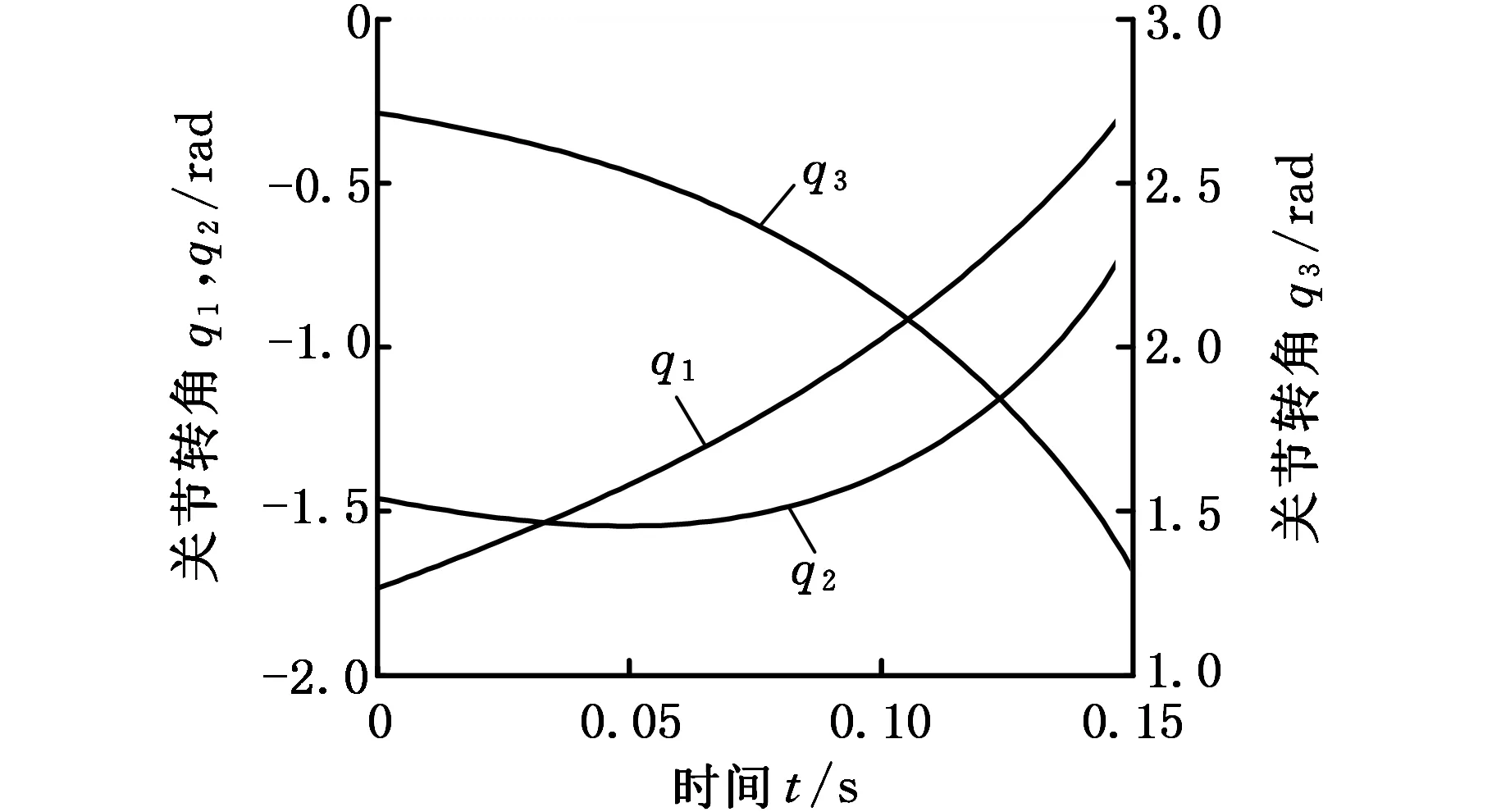
(a)髋关节和踝关节驱动

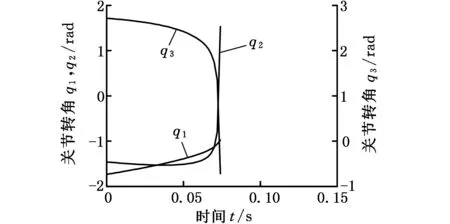
(b)髋关节和趾关节驱动

(c)踝关节和趾关节驱动图2 不同驱动器配置下关节转角运动规律的比较Fig.2 Comparison of joint angle of different actuator placements

图3为不同驱动器配置下的弹跳机器人起跳姿态图。可以看出：图3a采用髋关节和踝关节驱动比较合理，机器人脚杆的转动和腿杆与躯干均处于持续前伸的过程，各杆的运动规律都十分平滑，与生物的运动形态规律[2]相当吻合；而且采用髋关节和踝关节驱动，两驱动器在结构设计时可近躯干方向布局，有利于减小腿部的质量及其摆动时的转动惯量，从而减小其驱动力矩并改善机动性，使机器人更容易弹跳，故这种配置是最为合理的。图3b在同等条件下机器人的趾关节和踝关节运动虽然比较正常平稳，但其运动时间段较短，脚和腿的运动幅度也相对较小，而其躯干则水平加速前移而无抬起趋势，故不能起跳。机器人在此之后延续运动的时间里其姿态将会变得混乱。图3c在髋关节被动的情况下，机器人的脚几乎不转动，此时腿转动且转动幅度较小，而其躯干则由起跳运动姿态的起始位置(图中带有“○”的位置)先向前运动一小段距离，然后就有向后倒的运动趋势，而且与图3b存在同样的运动时间段较短问题。加之机器人身体的惯性很大(一般身体质量约占总质量的85%)，踝关节和趾关节驱动情况下，容易使得机器人向后倾倒，故第3种驱动配置属于三者中最差的一种配置。综上可知，在考虑机器人驱动器配置时，采用髋关节和踝关节驱动是最好的一种配置方式。在此配置情况下，由于跳跃机器人髋关节主要起调整身体姿态的作用，而踝关节则主要起驱动的作用：在着地起跳阶段，髋关节基本处于无驱动状态，而整个机器人的起跳动力主要由踝关节提供；进入腾空阶段，髋关节发力并用于提腿进而向前迈腿实现空中调姿，而踝关节此时处于无驱动状态。可见，采用髋关节和踝关节驱动配置，在机器人跳跃过程中这两个关节非同时发力而是一个分段交替发力过程，也是一个二次欠驱动的过程，机器人跳跃实质上总是同时仅有一个驱动器发力，因而髋关节和踝关节双驱动对机器人的动力能源分配极为合理，具有生物节能优势。

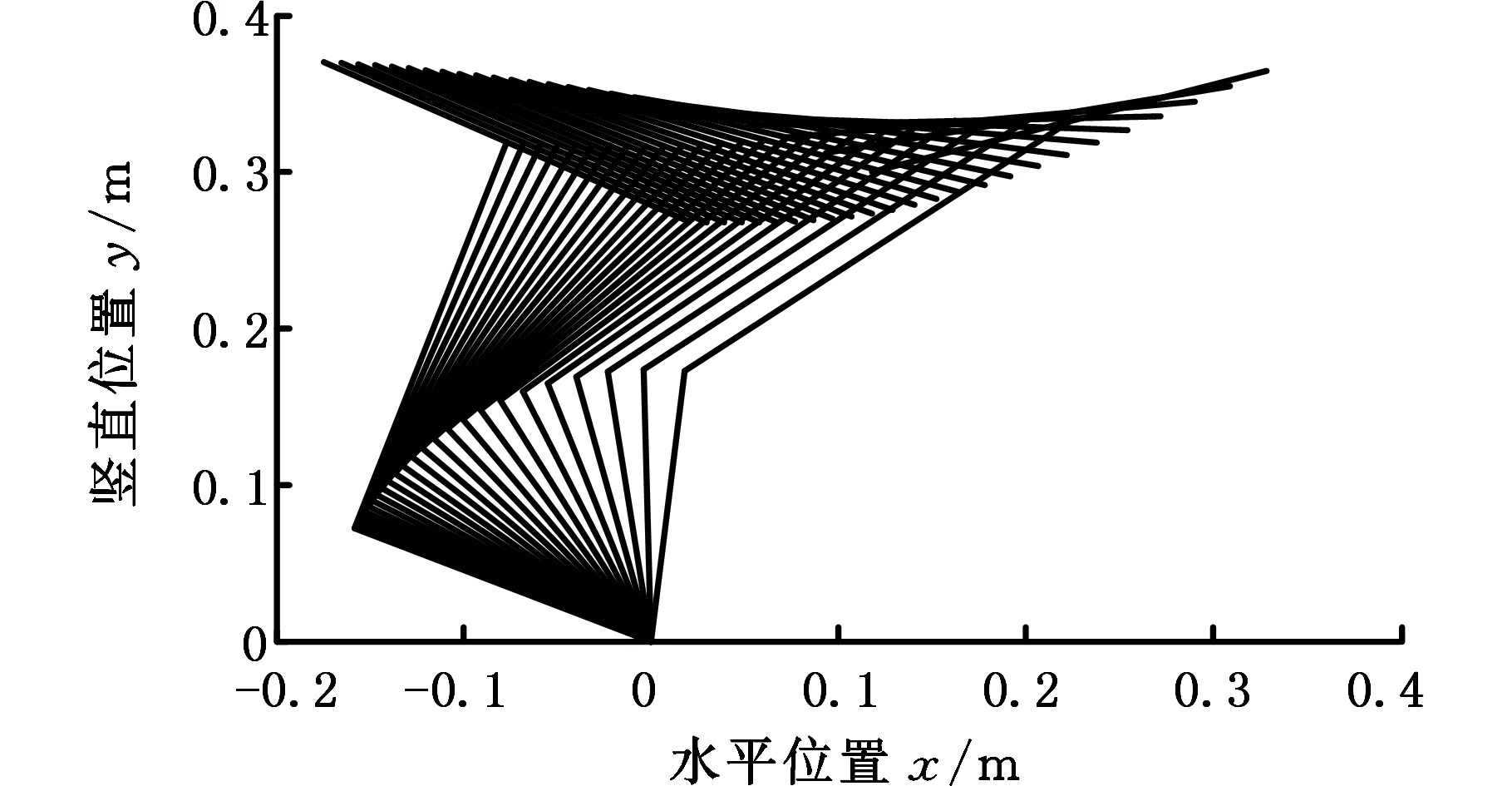
(a)髋关节和踝关节驱动

(b)髋关节和趾关节驱动

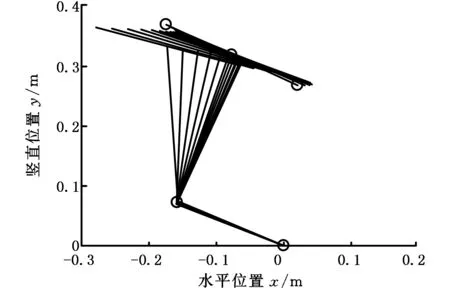
(c)踝关节和趾关节驱动图3 不同驱动器配置下姿态图的比较Fig.3 Comparison of posture of of different actuator placements

图4所示为不同驱动配置情况下机器人起跳过程中两主动关节的驱动力矩变化曲线。其中图4a所需的驱动力矩较小，髋关节和踝关节的最大驱动力矩分别是32.4215 N·m和17.6281 N·m，是三种驱动配置情况下的驱动力矩最小的。图4c中踝关节和趾关节所需的驱动力矩的最大值分别是215.3394 N·m和314.8706 N·m，是三种驱动配置情况下的驱动力矩最大的。需要说明的是，图4b中在0.06 s后出现的力矩突变曲线，表明由此之后规律实际上不存在。综上，采用髋关节和踝关节驱动配置时所需的驱动力矩最小，是最好的动力配置方案，其运动及动力规律均符合生物运动及发力的动力学先进机理，且能实现仿生起跳姿态。其他两个驱动器配置方案都存在不合理之处，尤其是第三种方案，尽量不采用。

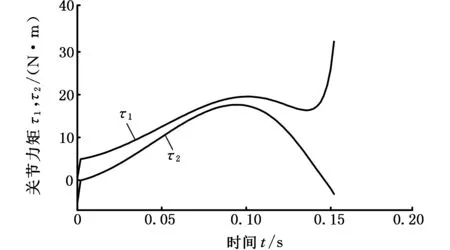
(a)髋关节和踝关节驱动

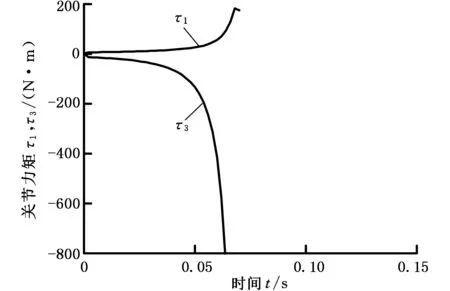
(b)髋关节和趾关节驱动

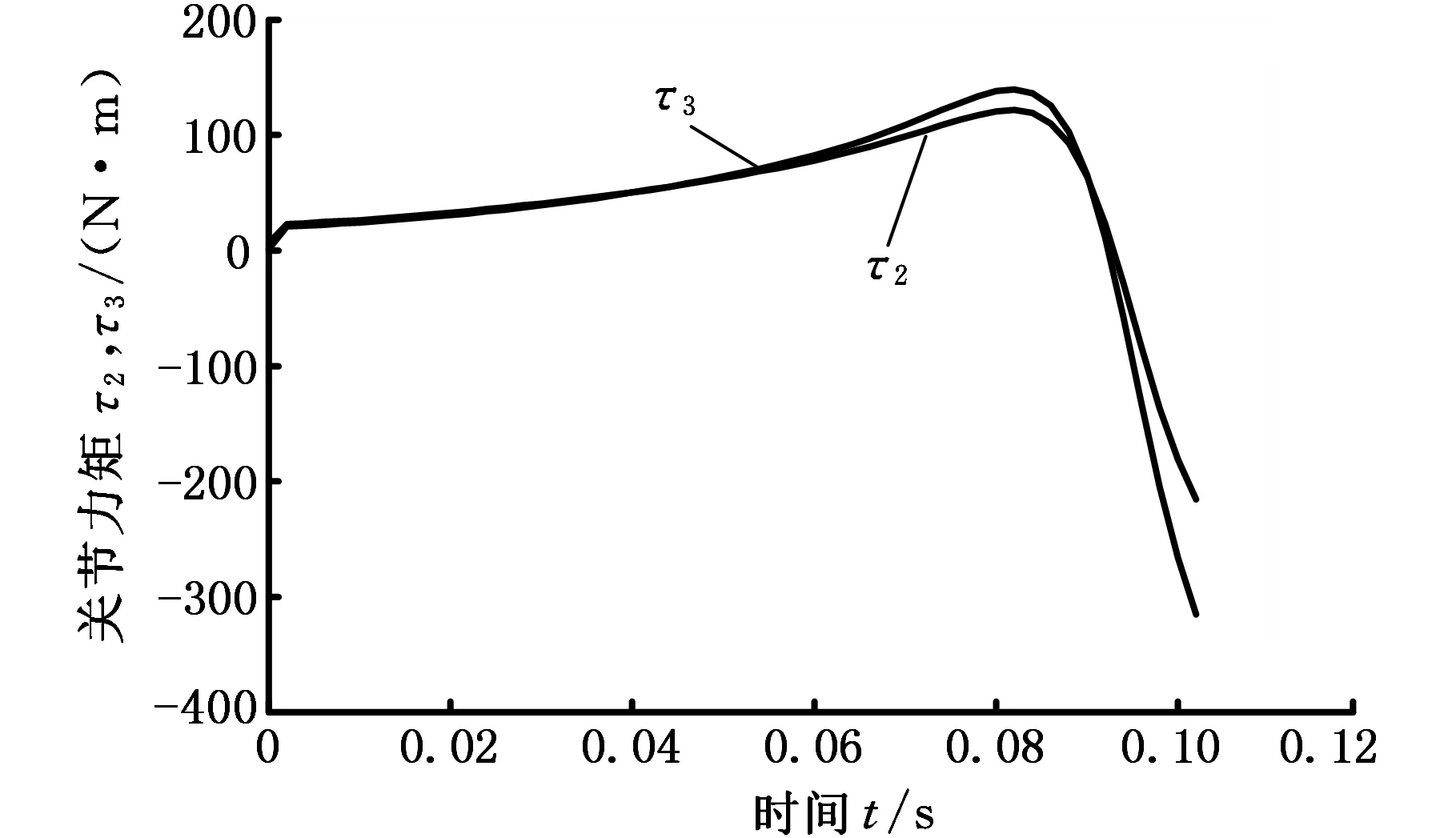
(c)踝关节和趾关节驱动图4 不同驱动器配置下关节驱动力矩的比较Fig.4 Comparison of driving torque of different actuator placements

4 结论

(1)本文提出的运动规划方法是可行的和有效的，具有计算快速简单的优点；只要给定机器人质心初始位置和速度以及质心运动轨迹，即可得到机器人在起跳阶段转角运动规律。

(2)采用髋关节和踝关节作为驱动关节时，弹跳机器人运动符合生物运动规律，驱动力矩在三者之中最小，能够达到起跳时的速度和加速度，能顺利实现起跳，且这种布置有利于驱动器向躯干方向布置，有利于腿部质量和转动时转动惯量的减小，是三种情况中最合理的；而其他两种情况都存在运动时间较短、驱动力矩较大的问题，采用髋关节和趾关节驱动姿态比较合理，但后期会导致驱动力矩过大，若采用踝关节和趾关节驱动，机器人会先向前运动然后向后倒，无法实现起跳，所以这两种驱动器配置方式效果均不佳。

[1] VERMEULEN J. Trajectory Generation for Planar Hopping and Walking Robots: an Objective Parameter and Angular Momentum Approach[D]. Brussel: Vrije Universiteit,2004.

[2] 葛文杰.仿袋鼠跳跃机器人运动学及动力学研究[D]. 西安: 西北工业大学,2006. GE Wenjie. Research on Kinematics and Dynamics of a Kangaroo Hopping Robot[D]. Xi’an: Northwestern Polytechnical University,2006.

[3] 魏敦文，葛文杰. 跳跃机器人研究现状和趋势[J]. 机器人, 2014,36(4): 503-512. WEI Dunwen,GE Wenjie. Research Status and Development Trend of Hopping Robots[J].Robot,2014,36(4):503-512.

[4] 王申江, 郭祖华. 单腿跳跃机器人轨迹规划[J]. 中国机械工程, 2015,26(17):2330-2335. WANG Shenjiang, GUO Zuhua. Trajectory Planning for an One-legged-hopper Robot[J].China Mechanical Engineering,2015,26(17):2330-2335.

[5] BERGERMAN M, XU Y S.Planning Collision-free Motions for Underactuated Manipulators in Constrained Configuration Space[C]//Proceedings of the 1997 IEEE International Conference on Robotics and Automation. Albuquerque,1997:549-555.

[6] YOSHIKAWA T, KOBAYASHI K, WATANABE T. Design of a Desirable Trajectory and Convergent Control for 3-DOF Manipulator with a Nonholonomic Constraint[C]// Proceedings of the 2000 IEEE International Conference on Robotics and Automation. San Francisco,2000:1805-1810.

[7] LYNCH K M, SHIROMA N, ARAI H, et al. Collision-free Trajectory Planning for a 3-D of Robot with a Passive Joint[J]. International Journal of Robotics Research,2000,19(12):1171-1184.

[8] LUCA D A, ORIOLO G.Trajectory Planning and Control for Planar Robots with Passive Last Joint[J]. The International Journal of Robotics Research,2002,21(5/6):575-590.

[9] NISHIDA Y, NAGAMATU M.Trajectory Planning with Dynamics Constraints for an Underactuated Manipulator[J]. Lecture Notes in Computer Science,2008,5506:787-793.

[10] GREGORY J, OLIVARES A, STAFFETTI E. Energy-optimal Trajectory Planning for Planar Underactuated RR Robot Manipulators in the Absence of Gravity[J]. Abstract and Applied Analysis,2013,2013(3):360-374.

[11] 何广平, 陆震,王凤翔.欠驱动余度机械臂的无碰撞运动规划与控制[J]. 机械工程学报, 2005,41(6):208-213. HE Guangping, LU Zhen, WANG Fengxiang. Motion Planning and Control of Underactuated Redundant Manipulators with Obstacle Avoidance[J].Chinese Journal of Mechanical Engineering,2005,41(6):208-213.

[12] 陈伟.欠驱动平面耦合刚体动力学与运动规划研究[D].北京：北京机械工业学院，2006. CHEN Wei. Study on Dynamics and Motion Planning for Planar Underactuated Coupled Rigid Bodies[D]. Beijing:Beijing Information Science and Technology University,2006.

[13] 刘庆波. 水平运动的欠驱动机器人运动规划与控制研究[D].北京:北京工业大学,2009. LIU Qingbo. Motion Planning and Control of Horizontal Underactuated Robots[D].Beijing: Beijing University of Technology,2009.

[14] WU T Y, YEH T J, HSU B H.Trajectory Planning of a One-legged Robot Performing a Stable Hop[J].The International Journal of Robotics Research,2011,30(8):1072-1091.

[15] 刘载淳.欠驱动跳跃机器人的运动轨迹规划及试验研究[D].哈尔滨:哈尔滨工业大学,2011. LIU Zaichun. Trajectory Planning and Experiment Research of Underactuated Hopping Robot[D].Harbin: Harbin Institute of Technology,2011.

[16] HE Guangping, GENG Zhiyong.Dynamics Synthesis and Control for a Hopping Robot with Articulated Leg[J]. Mechanism and Machine Theory,2011,46(11):1669-1688.

(编辑 陈 勇)

Actuator Configuration of Optimal Motion Posture for Underactuated Hopping Robots

MENG Xiangyan GE Wenjie

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, 710072

This paper dealt with the trajectory planning problems of three joints underactuated hopping robots with one passive joint. Firstly, the dynamics model of the robot was established. Secondly, the angles of three joints were obtained by the numerical iterative method and the optimization objective was minimization of the active joint torques. Finally the joint angle trajectory, motion postures and driving torques of three kinds of actuator configurations were obtained by simulation, then the differences were analyzed and compared. The results show that the proposed motion planning method is feasible, and the hopping robot with actuation at hip and ankle is the most reasonable.

hopping robot; trajectory planning; underactuated; stance phase

2016-10-31

国家自然科学基金资助项目(50975230)；高等学校博士学科点专项科研基金资助项目(20136102130001)

TP242

10.3969/j.issn.1004-132X.2017.15.001

孟祥艳，女，1985年生。西北工业大学机电学院博士研究生。主要研究方向为弹跳机器人、仿生机器人。E-mail: xym_02@126.com。葛文杰，男，1956年生。西北工业大学机电学院教授、博士。