Cancelable remote quantum fingerprint templates protection scheme∗

Qin Liao(廖骎),Ying Guo(郭迎),†,and Duan Huang(黄端),2,‡

1 School of Information Science and Engineering,Central South University,Changsha 410083,China

2 State Key Laboratory of Advanced Optical Communication Systems and Networks,and Center of Quantum Information Sensing and Processing, Shanghai Jiao Tong University,Shanghai 200240,China

Cancelable remote quantum fingerprint templates protection scheme∗

Qin Liao(廖骎)1,Ying Guo(郭迎)1,†,and Duan Huang(黄端)1,2,‡

1 School of Information Science and Engineering,Central South University,Changsha 410083,China

2 State Key Laboratory of Advanced Optical Communication Systems and Networks,and Center of Quantum Information Sensing and Processing, Shanghai Jiao Tong University,Shanghai 200240,China

With the increasing popularity of fingerprint identification technology,its security and privacy have been paid much attention.Only the security and privacy of biological information are insured,the biological technology can be better accepted and used by the public.In this paper,we propose a novel quantum bit(qbit)-based scheme to solve the security and privacy problem existing in the traditional fingerprint identification system.By exploiting the properties of quantum mechanics,our proposed scheme,cancelable remote quantum fingerprint templates protection scheme,can achieve the unconditional security guaranteed in an information-theoretical sense.Moreover,this novel quantum scheme can invalidate most of the attacks aimed at the fingerprint identification system.In addition,the proposed scheme is applicable to the requirement of remote communication with no need to worry about its security and privacy during the transmission.This is an absolute advantage when comparing with other traditional methods.Security analysis shows that the proposed scheme can effectively ensure the communication security and the privacy of users’information for the fingerprint identification.

quantum communication,fingerprint identification,cancelable template

1.Introduction

With the continuous development of biological technologies and artificial intelligence,fingerprint identification technology has been commonly used by the public.Compared with the traditional identity authentication methods using passwords or character string,the usage of fingerprint identification is simple,convenient,and without having to make extra efforts in memorizing,because only with the scanning of the user’s finger over the sensor,the identity authentication process will be completed.However,the biological technology does not equal to absolute security and it also has several intrinsic problems.For example,the original feature data of the fingerprint(called‘minutiae’)are usually stored in the database of servers,if the database is compromised,all feature data from fingerprints will be exposed,[1]eavesdroppers,then, can restore the original fingerprint images by using these exposed and compromised minutiae.Therefore,it will never be secure once the original fingerprint images are compromised.

To overcome the mentioned problems,a technology called revocable biological template protection has been proposed.[2]This technology protects user’s security and privacy by using irreversible template transformation of minutiae.In the process of fingerprint identification,only the transformed template is used for authentication.By doing this, compromise and exposure of minutiae can be prevented.The advantage of this scheme is that a renewed irreversible transformed template will be generated from records of the same minutiae once the transformed template is exposed.In recent years,a fingerprint identification algorithm by exploiting biological features template protection technology has become a hot-spot,researchers have proposed various strategies to protect the biological features template,and these strategies can be categorized into two types:[3](i)transformation of biological features[4–9]and(ii)the methods based on helper data.[10–15]However,these classical security schemes still have problems.For example,in the first type,bio-hashing of biological features[6]is proposed in which one can combine random number and fingerprint images to create the template.However,eavesdroppers can easily attack the system if he/she has obtained the identity token.Chulhan et al.[8]came up with an idea of reflecting the minutiae into a three dimensional array and combining the personal PIN code to obtain a transformed bit string.This scheme still has weakness, once the PIN code is reset,the security of the system could be greatly reduced.For the second type,Yang et al.[13]proposed a Delaunay quadrangle-based fingerprint authentication system,which expands the Delaunay triangle-based structure proposed in Refs.[14]and[15].The local Delaunay quadrangle based structure has better structural stability than the Delaunay triangle-based structure and it is able to tolerate a certain extent of nonlinear distortion-induced structural change,but lots of parameters in this method need to be set which thus may lead to complexity and expenditure problems.Generally speaking,the two types of protection strategies both have in-trinsic weaknesses,which to some degree causes security and privacy issues for the biological characteristics template.

By contrast with the above-mentioned classical methods, in the field of physics,meanwhile,quantum mechanics is a set of theories established at the beginning of 20th century.[16]After the development of a century,it has become one of the sub-disciplines of physics,which focuses on researching the movement pattern of micro-particles in the material world.[17]Quantum mechanics is not only one of the basic theories in modern physics,but also has wide applications in relevant disciplines(e.g.,chemistry and cryptology)as well as many modern technologies.[18]Interestingly,the micro-particles have lots of strange properties which could provide new methods to solving the classical problem.[19,20]Inspired by distinct properties of quantum,Bennett and Brassard proposed a quantum method to solve the problem of key distribution;their research results were published as the well-known BB84 protocol,[21]which encodes information by exploiting the complementarity of two states of a linearly polarized photon(horizontal and vertical directions)and two states of a circularly polarized photon (levorotary and dextrorotary directions).This protocol has a profound impact on the discrete-variable quantum key distribution(DVQKD)area.For decades,researchers have put forward lots of improved DVQKD protocols.Meanwhile,the unconditional security proofs for this type of protocols have steadily improved and today unconditional security,namely, the security guaranteed in an information-theoretical sense, has been established for DVQKD protocols in both asymptotic limit[22]and finite-size regime.[23,24]Our quantum fingerprint templates protection scheme can be deemed as an application of the DVQKD protocol in fingerprint identification area.Thus,from this viewpoint,our scheme not only can well defend most specific attacks aimed at the fingerprint identification system,but also can defend the collective attacks which are the most powerful attacks to the DVQKD protocols.

In what follows,we detail the proposed novel cancelable remote quantum fingerprint templates protection scheme, which can theoretically guarantee the security and privacy of the fingerprint identification system.The organization of this paper is as follow.In Section 2,we briefly describe several quantum properties related to our works.The novel quantum fingerprint templates protection scheme is detailed in Section 3.Security analysis is presented in Section 4 and the conclusion is given in Section 5.

2.Quantum properties

Details about quantum mechanics can be found in Ref.[17].In this section,we only discuss several basic quantum properties related to the proposed scheme,and they are significant for the design of a quantum fingerprint recognition system.

2.1.Uncertainty principle

In order to acquire the information encoded in quantum bit|ϕ〉,we must measure this quantum bit.Given a measurement operator Q,let|qi〉(i=1,2,...,n)be Q’s eigenstates, then arbitrary quantum bit|ϕ〉can expand according to the eigenstate of Q,namely,

If at least two items in ci(i=1,2,...,n)are not 0,|ϕ〉is certainly not the eigenstate of operator Q.Let|ϕ〉be an eigenstate of measurement operator L,namely,

Since|qi〉(i=1,2,...,n)is a set of orthonormal basis,which is linear independence and can expand a linear space.But |ϕ〉and|qi〉(i=1,2,...,n)cannot be orthonormalized due to Eq.(1).Thus,they cannot be the eigenstate of Q and L simultaneously.In quantum mechanics,this situation is called that Q and L cannot be commuted,namely,

Hence,Q and L cannot be measured simultaneously.That is to say,the measurement result of|ϕ〉using the measurement basis corresponding to Q as the measurement operator is different from the measurement result of|ϕ〉using the measurement basis corresponding to L as the measurement operator.

For example,consider a basic quantum bit which could be|0〉or|1〉,their corresponding probabilities are‖α‖2and‖β‖2,respectively.According to the superposition principle,this quantum bit also could be the linear state α|0〉+β|1〉, but we cannot exactly know which state it is without measurement.Quantum measurement is related to the option of measurement basis,that is to say,if we choose an improper basis, we cannot obtain the precise result.Figure 1 shows that an arbitrary quantum bit|ψ〉in a two-dimensional Hilbert space can be represented by a vector|ψ〉=α|0〉+β|1〉(orange arrow) which consists of base|0〉and base|1〉(black solid coordinate axes).As a result,the measurement result is either|0〉or|1〉when one chooses the basis|0〉〈0|and|1〉〈1|to measure|ψ〉. However,since the amplitude and phase are not commuted, we can only obtain the precise result of the amplitude while the phase is uncertain.But if using{|0′〉,|1′〉}(blue dashed coordinate axes)as the measurement basis,|ψ〉can be absolutely determined.This is because quantum bit|ψ〉can be represented by|ψ〉=α′|0′〉,which is one of the orthogonal basis {|0′〉,|1′〉}.Hence,the amplitude and phase can be precisely measured in{|0′〉,|1′〉}rather than{|0〉,|1〉}.

Fig.1.(color online)Uncertainty principle of quantum bit.

The property of imprecise measurement of quantum bit is determined by uncertainty principle.This speciality renders the quantum bit completely different from a classical bit.[25]For a classical bit,on which most cancelable fingerprint templates protection methods are based,it can be measured precisely under any situation.A classical binary bit only can be‘1’or‘0’.However,for a quantum bit,it is impossible to obtain accurate information if improper measurement basis is chosen.The uncertainty principle is the quantum’s inherent nature.Although this property may cause some difficulties in quantum computing,it provides novel ideas in security communication area.

2.2.No-cloning theorem

In quantum physics,the no-cloning theorem states that it is impossible to create an identical copy of an arbitrary unknown quantum state.

Suppose that a clone-wanted quantum state is arbitrary quantum bit|Ψ〉,and the initial quantum bit state of the clone particle is|s〉.The objective of the quantum clone is to transform|s〉to|Ψ〉under the impact of unitary transformation U without destroying the clone-wanted quantum state,namely, the following process:

which is impossible.

No-cloning theorem is an inherent property of quantum mechanics,which is as if one has set an insurmountable limitation.This theorem is one of the bases of quantum information science,which guarantees the security of quantum cryptogram and makes it impossible for an eavesdropper to acquire legal user information through clone technology.[26]Hence,it provides a qualitative safeguard for quantum fingerprint template protection scheme.

2.3.Entanglement

A basic quantum bit is made up of a single quanta,while the composited quantum bit is compounded by n quantum bits, which can be expressed as

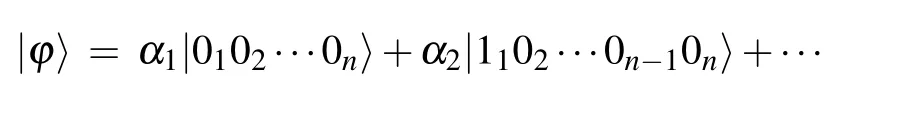
where m≤n,subscripts represent different quantum.

There is a special kind of composited quantum bit, namely,the entangled state.Therein to,EPR entangled pair is the most representative entangled quantum bit,which can be represented as follows:

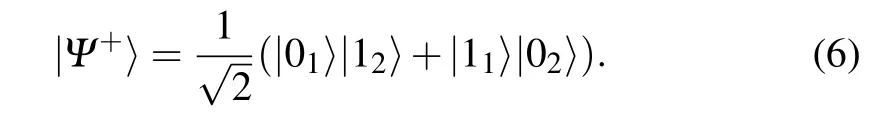
The characteristic of this system is that when particle 1 is in the state|0〉,particle 2 is inevitably in the state|1〉;and when particle 1 is in the state|1〉,particle 2 is inevitably in the state |0〉.However,the quantum state will collapse into a sort of eigenstate after measurement operation and it is no longer capable to turn back to the original state anymore.[27]

3.Quantum fingerprint system

In this section,we detail the remote quantum fingerprint templates protection scheme.This scheme encodes the traditional minutiae feature in quantum bits and utilizes inherent properties of quantum bit to ensure the system’s security and privacy.Therefore,this scheme not only can be deployed independently,but also adapt to most existing classical minutiae extraction algorithms.Meanwhile,we creatively propose the concept of quantum remote fingerprint verification,namely, the minutiae extraction device(client)and the fingerprint verification device(server)do not need to deploy at the same place,which could meet the demand of remote authority.

Although the proposed scheme does not involve concrete physical implementation,the complementarity of two states of linearly polarized photon|↑〉,|→〉(horizontal and vertical directions)and two states of circularly polarized photon|↗〉,|↘〉(levorotary and dextrorotary directions)can be used(not limited to use)to illustrate the principle of the scheme.[28]Therein to,two states of linearly polarized photon and two states of circularly polarized photon are orthogonal respectively,while the states of linearly polarized photon and the states of circularly polarized photon are not orthogonal, namely,

where x∈{↑,→}and y∈{↗,↘}represent the states of linearly polarized photon and circularly polarized photon,respectively.

The states of linearly polarized photon and circularly polarized photon are conjugate states,which meet the uncertainty principle discussed in Section 2.The more precise the measurement of linearly polarized photon means the less precise of that of circularly polarized photon and vice versa.That is to say,a certain result can be obtained when measurement basis⊥for a linearly polarized photon is adopted to measure the linearly polarized photon,while,due to the uncertainty principle,the result is uncertain if measurement basis⊥is adopted to measure the circularly polarized photon.Similarly,a certain result can be obtained when measurement basis○for circularly polarized photon is adopted to measure circularly polarized photon while the result is uncertain if measurement basis○is adopted to measure linearly polarized photon.

We define an interconversion rule:|→〉→0,|↗〉→0, |↑〉→1,|↘〉→1,which is used to interconvert the presentation of four polarized photon states and classical binary bit. Subsequently we introduce the concept of decision sequence. The role of the decision sequence is to determine which polarized photon state is used to denote 0 or 1.According to the interconversion rule mentioned above,′C′means using two states of circularly polarized photons(|↗〉and|↘〉)to denote classical bits,while′H′means using two states of linearly polarized photons(|→〉and|↑〉)to denote classical bits.For example,Table 1 shows that the minutiae binary bit string{0 1 1 0 0 1}(note that the length of a genuine bit string after minutiae extraction is much longer than the example bit string)is translated into quantum bit string{|→〉|↘〉|↑〉|→〉|↗〉|↘〉}by using decision sequence[H C H H C C].

Our proposed scheme consists of two modules,one is afingerprint extraction module(client)and the other is a fingerprint recognition module(server).The former module could be considered as a small portable device,and its main function is to extract and translate original fingerprint features(minutiae)and execute necessary communication with the server. The role of the latter module is similar to the cloud server in cloud computing technique,its main task is fingerprint identification.Having these two modules,users could fulfill various objectives such as remote authority,unlock,and recognition through scanning their fingerprints on portable micro devices. The security and privacy of telecommunication,which will be elaborated at Section 4,can be guaranteed by the proposed scheme.Similarly with most traditional template protection methods,the proposed quantum template protection scheme is also divided in two stages,which are the enrollment stage and the verification stage.We detail each stage as follows.

Table 1.Interconversion between classical binary bit and quantum bit.

3.1.Enrollment stage

At the enrollment stage,a decision sequence and a measurement basis sequence are produced by the client and the server respectively for each registrant.The procedure of the enrollment stage is shown in Fig.2 and the detail steps are explained below.

Fig.2.(color online)Enrollment stage.

1)The client firstly produces a random decision sequence for each fingerprint and then transmits the sequence to the server’s database through a classical channel.This sequence is used to decide which interconversion rule is used to transform the presentation from classical bit to quantum bit.After that, a classical binary bit string,which is acquired by minutiae extract,is transformed to the corresponding quantum bit string. Meanwhile,the server prepares a set of EPR entangled pairs according to each single quantum bit in the quantum bit string mentioned above.For each EPR entangled pair,the server transmits one of its particle|qa〉to the client through quantum channel and reserves|qb〉at its own quantum memory.By doing these,every binary bit corresponds to an EPR pair.

2)The server randomly produces a measurement basis sequence,subsequently saves it in the database and transmits its copy to the client through classical channel.The client measures each particle|qa〉successively using the corresponding measurement basis according to the measurement basis sequence.Owing to the property of EPR entanglement,which is discussed in Section 2,once a particle of EPR has been measured,another particle state can be confirmed.In this case, |qa〉has been measured,thus the state of|qb〉can be known without additional measurement.Note that the server actually does not know what the state is if the client does not tell it the result of measurement,so the server must utilize the corresponding measurement basis to measure|qb〉.Since each measurement basis of randomly produced measurement basis sequence probably cannot measure the quantum state precisely due to the uncertainty principle,the measurement result of server’s quantum bit string may contain several imprecise quantum states.Then,the server recovers the classical bit string according to the decision sequence produced in step 1), and saves it in database.After doing these,the key of each fingerprint has been formed and encrypted without using classical channel to transmit minutiae.The encrypted key is stored in server’s database.

3)Generate a cancelable template using the decision sequence and measurement basis sequence.Note that the lengths of both types of sequences are fixed according to the original fingerprint features.Each type of sequence is formed randomly and independently,which means each of them be reformed without affecting the other.Here we use an example to illustrate the generation of cancelable template.As can be seen from Fig.3,providing that the decision sequence is [H C H H C C H C C H]and the measurement basis sequence is[⊥⊥○⊥○⊥○○⊥○],we use these two sequences to generate a template.Firstly,these two sequences are translated into a binary string presentation.Let′1′indicate H and⊥,′0′indicate C and○.After doing this,a NOT gate is used to act on the translated decision sequence.A new binary string is generated by using the translated measurement basis sequence and inverse translated decision sequence as inputs through XOR gate.Finally,′0′in this novel binary string is replaced with′?′.In this case,template[1??1 1??1??] is generated.

Fig.3.(color online)Generate cancelable template.

3.2.Verification stage

At this stage,the primary task of the system is to identify whether users are legitimate or not.For each enrolled record in the server database,the procedure of verification stage is illustrated in Fig.4 and details are stated below.

1)The client prepares a set of EPR entangled pairs according to this record’s decision sequence and query fingerprint minutiae binary string.For each EPR entangled pair,the client transmits one of its particles|qb〉to the server through quantum channel and reserves|qa〉for itself.By doing these, every query fingerprint minutiae binary bit has an EPR pair counterpart.Then,the client possesses a quantum bit string |qa〉i(i=1,2,...,n)while the server possesses a corresponding quantum bit string|qb〉i(i=1,2,...,n),where n is the length of the classical binary bit string extracted from the query fingerprint.

2)The server utilizes each measurement basis in this record’s measurement basis sequence to measure the corresponding quantum bit in|qb〉i(i=1,2,...,n).After measurement,all these quantum bits are collapsed into the eigenstates of their corresponding measurement operators.Applying Pauli-X gate[28]to these collapsed quantum bits,subsequently,the quantum bits X|qb〉iare translated into a classical binary bit string according to the interconversion rule.By these two steps,an encrypted and specific binary bit string for the current record has been produced.This binary bit string is called the query code.

Fig.4.(color online)Verification stage.

Table 2.Matching process.

3)The final step of the verification stage is to match the query code and record’s encrypted key.Assume that BErepresents the encrypted key,BQrepresents the query code,and BTrepresents the template.The matching process is shown in Table 2.After obtaining four substrings,SE,SQ,UE,UQ, two similarity matrices are proposed to determine whether the record belongs to the current user or not.The similarity matching scores can be calculated as follows:

where·represents a bit-wise XOR-NOT operator.∑(□·□) counts the positions that have a value 1 in the operate result and sums them up.n and m denote the lengths of the template and the number of 1 in the template,respectively.s(SE,SQ) ranges from 0 to 1,where‘1’indicates a perfect match.We propose another metric s(UE,UQ)here to avoid the situation that once an encrypted key stored in the server database is compromised,an adversary may try to login in using this encrypted key,which makes the value of s(UE,UQ)be‘1’.That is to say,if the value of s(UE,UQ)is larger than a certain threshold tscore(0＜tscore＜1),this verification can be considered as a failure.

4.Security analysis

In this section,we elaborate the security analysis of the proposed cancelable remote quantum fingerprint templates protection scheme.The security of this scheme can be discussed from two aspects,one is unconditional security in quantum communication,and the other one is specific security against fingerprint system.We show the unconditional security of our proposed scheme first.

As we mentioned in Section 1,our proposed scheme is based on the discrete-variable quantum key distribution protocol,in particular the well-known BB84 protocol.The method that we use qbits to transmit minutiae is similar to the method that the BB84 protocol uses qbits to encode communication information.From this viewpoint,the proposed cancelable remote quantum fingerprint templates protection scheme can be deemed the practical application of the BB84 protocol for which unconditional security has already been proved.[22–24]Thus,our scheme also has unconditional security which means the security is not based on the computational power or quan-tum memory power but guaranteed by the quantum nature.

On the other side,owing to the speciality of quantum technique and the limitation of our laboratory,we cannot directly test the performance of the proposed scheme by using authentic fingerprint data,e.g.,FVC2002 and FVC2004.Instead,we give the detailed specific security analysis in fingerprint system of our proposed scheme.

The specific security analysis in fingerprint system includes four aspects,which are briefly summarized as follows.

Diversity Cross-matching between templates from the same user across different applications must be prevented.

Remoteness It should allow users to login to the system remotely.

Cancelability A new template can be reissued once the obsolete template is compromised.

Irreversibility It should be computationally infeasible or hardly realizable to derive the original biometric information from the encrypted key.

In what follows,we discuss the specific security analysis of our proposed scheme.

4.1.Security against specific attacks aimed at fingerprint system

Our proposed scheme must guarantee the user’s privacy during the whole process of the quantum fingerprint system, therefore,several scenarios are considered to analyze the security against specific attacks aimed at the fingerprint system.

4.1.1.Lost quantum bit string attack

Assume that legal user’s quantum bit string is lost somehow.In this scenario,there is no need to be nervous only if the quantum bit string is stolen by eavesdropper.Actually,legal user’s quantum bit string is useless for the eavesdropper without knowing any other extra information.Since this string is formed by a set of EPR pairs according to a certain decision sequence and the interconversion rule,the eavesdropper cannot recover original biometric information from this quantum bit string because the formation rules are unknown.For the eavesdropper,he does not even know the state of each quantum bit in this string,he can only randomly choose a certain measurement basis to measure the quantum bit one-by-one. The probability of choosing the correct measurement basis for all quantum bits is 1/2n,where n represents the length of the quantum bit string,it would not be a likely achievement in practice.Moreover,the entanglement of the EPR pair will no longer exist once a certain particle in the EPR pair has been measured and this particle’s quantum state will collapse.That is to say,if the eavesdropper chooses at least one improper measurement basis,he not only cannot acquire the correct result but also irreversibly changes this quantum bit string.On the other hand,some attackers may want to copy this quantum bit string as classical binary bit string.This process is impossible according to no-cloning theorem.Thus,security can be guaranteed in this scenario.

4.1.2.Lost decision sequence or measurement basis sequence attack

Consider two scenarios,which are lost decision sequence or lost measurement basis sequence,respectively.Each legal user corresponds to a unique PIN stored in the server database, every PIN is related to a decision sequence and a measurement basis sequence.If the decision sequence is stolen by an eavesdropper,all he knows is just the rules how to generate the EPR quantum bit string.On the other hand,if the measurement basis sequence is stolen,the eavesdropper can only be aware of which measurement basis can measure the quantum bit correctly.The eavesdropper actually does not know the user’s biometric information in both cases because these two sequences completely do not contain any minutiae information.That is to say,even though the eavesdropper knows the rules of how to generate the EPR quantum bit string or how to measure each quantum bit for a legal user,he still cannot recover a user’s original biometric information and thus cannot get successful access to the system.

4.1.3.Template is compromised

The template is formed by the decision sequence and the measurement basis sequence through some bit-wise operators, as shown in Fig.3.The function of the template is to decode the encrypted key and extract the matching information. An eavesdropper could locate the position of the measured quantum bit which uses the proper measurement basis if the template is compromised.However,because the eavesdropper does not know the corresponding encrypted key,he still cannot obtain the final matching information.

4.1.4.Lost encrypted key attack

Lost encrypted key attack is the most dangerous situation in all attacks.This is because once the eavesdropper has acquired someone’s encrypted key,he can bypass all the former steps and directly use this encrypted key to start matching. Due to two identical encrypted keys as the matching step’s input,the score of s(SE,SQ)equals 1,which means perfect match.But,meanwhile,the score of s(UE,UQ)also equals 1,which is larger than threshold tscore.In this situation,the eavesdropper will be denied access to the system.

4.2.Diversity

Our proposed scheme is applicable to different applications simultaneously.Due to the randomness of the generation of decision sequence and measurement basis sequence,templates generated by different applications are also different, even these templates are generated from the same fingerprint image.As a result,the final encrypted keys from the same fingerprint image are also different,which means an individual is allowed to enroll different templates by using the same finger for different applications without cross-matching.This feature provides the security on which even if the eavesdropper has obtained a template of the user in an application,he still cannot use this template to access other applications which the same user has enrolled using the same fingerprint.

4.3.Remoteness

An advantage of our quantum fingerprint system is remoteness.Users can carry a little device featured with client function or a mobile phone integrated client function to login the quantum fingerprint system remotely.For example,a user can unlock their house door remotely or absently authorize someone to do something with this system.The traditional fingerprint system may also do these things,but there is an important problem that cannot be ignored in the remote respect,that is,communication security.The traditional remote fingerprint system needs to transmit user’s minutiae information(translated or untranslated)to the server,which is a high risk process.In this step,an eavesdropper could intercept the information,even steal or revise it in order to get a fake access.Although some systems transmit information with classical cryptographic algorithm,the eavesdropper still has a chance to crack it.[29]Moreover,a stolen minutiae information can be copied by the eavesdropper,whenever the attacker wants to access the system,he can use the copy to login in.

In our proposed remote quantum fingerprint system,communication can be guaranteed by the unconditional security of quantum communication.[27]As can be seen in Figs.2 and 4, no matter at which stage,only decision sequence and measurement basis sequence are transmitted through classical channel.These two sequences might be stolen by an eavesdropper during the transmission,which could lead to lost decision sequence or measurement basis sequence attack and compromised template discussed above.Nevertheless,our system can handle both situations well according to the corresponding analysis.

There is one step in both enrollment stage and verification stage in which we need to transport quantum bits using quantum channel,that is,when a side has prepared EPR quantum bits,each particle in a single EPR quantum bit must be transported to the other side through the quantum channel.Granted that an eavesdropper has acquired the entire quantum bit string somehow,he still cannot copy this quantum bit string on account of no-cloning theorem.Furthermore,the eavesdropper will know nothing about the state of each particle in this quantum bit string,because once he measures these particles using an improper measurement basis,they will collapse into uncertain states and the original quantum state cannot be recovered.

In addition,note that user’s minutiae features actually do not transmit through either classical channel or quantum channel,which means an eavesdropper has no chance to acquire the user’s related fingerprint data during the communication process.The technique,which ensures fingerprint minutiae communication without passing any channel,is called quantum teleportation.[30–32]

Therefore,the security of remote communication of the quantum fingerprint system can be guaranteed by the inherent properties of quantum bit.

4.4.Cancelability

One may consider a kind of situation in which an eavesdropper has obtained a legal user’s encrypted key;he could modify a few bits to let s(SE,SQ)get bigger and s(UE,UQ)less than threshold tscore.By doing this,the eavesdropper may get access to the system.This is a very dangerous attack.Fortunately,the proposed cancelable quantum fingerprint templates protection scheme can well handle this problem.When the system is compromised,all the current information including two kinds of sequences,template,and encrypted key can be discarded and subsequently a set of new information can be regenerated by changing randomly the formed decision sequence and measurement basis sequence.In addition,the latest information is uncorrelated to the compromised information although it is actually derived from the same original fingerprint.Hence,even if the eavesdropper obtained the encrypted key,he still cannot access the system as long as the system renews the encrypted key in time.

4.5.Irreversibility

At the lost encrypted key attack,although the eavesdropper knows the encrypted key,he still can hardly derive the original biometric information(classical binary bit string as an input to this system),even if he knows the corresponding template.This feature is called irreversibility,which is guaranteed by uncertainty principle.This is because each bit in the encrypted key is formed by different measurement basis,the measurement result cannot be sure if the selected measurement basis is improper to the corresponding polarized photon state. Thus,the eavesdropper cannot recover the original classical binary bit string.If the eavesdropper mandatorily recovers the original classical binary bit string regardless of uncertainty principle,he will obtain a string of fragmentary and useless bits.

5.Conclusion

We proposed a cancelable remote quantum fingerprint templates protection scheme by exploiting the inherent prop-erties of quantum state,specifically the uncertainty principle, no-cloning theorem,and entanglement.The proposed scheme has provided a novel orientation and idea for cancelable fingerprint verification system.By taking advantages of quantum techniques,the complexity of fingerprint identification system could be simplified tremendously and,foremost,the security and privacy of the system can be protected unconditionally. As the research goes on,there are several quantum communication techniques that can be considered to further improve the system.For example,a better scheme to defend the situation when n−m is too small at the matching step will be considered,and we will take the experimental implementation of our proposed scheme into account.Furthermore,in the future,we are planning to exploit continuous variable quantum information[33,34]to carry fingerprint feature minutiae, which is more compatible with standard telecommunication technologies and easy to implement.

[1]Cappelli R,Lumini A and Maltoni D 2007 IEEE Transactions on Pattern Analysis and Machine Intelligence 29 1489

[2]Ratha N,Connell J and Bolle R 2001 IBM Systems Journal 40 614

[3]K J A,Karthik N and Abhishek N 2008 Journal on Advances in Signal Processing 2008 1

[4]Nagar A,Nandakumar K,Jain A K 2010 Proceedings of SPIE-The International Society for Optical Engineering 7541 175

[5]Ang R,Safavinaini R and Mcaven L 2005 Information Security and Privacy,Australasian Conference,July 4–6,ACISP Brisbane,p.242

[6]Teoh A B J,Toh K A and Yip W K 2007 International Conference on Advances in Biometrics,Springer-Verlag,p.435

[7]Wang S and Hu J 2012 Pattern Recognition 45 4129

[8]Lee C and Kim J 2010 Journal of Network and Computer Applications 33 236

[9]Ratha N K,Chikkerur S,Connell J H and Bolle R M 2007 IEEE Transactions on Pattern Analysis and Machine Intelligence 29 561

[10]Jain A K,Ross A A and Nandakumar K 2011 Security Of Biometric Systems(New York:Springer)p.259

[11]Juels A and Sudan M 2004 IEEE International Symposium on Information Theory 38 408

[12]Dodis Y and Reyzin L 2004 Fuzzy Extractors:How to Generate Strong Keys from Biometrics and Other Noisy(Berlin:Springer)pp.97–139

[13]Yang W,Hu J and Wang S 2014 IEEE Transactions on Information Forensics and Security 9 1179

[14]Abellanas,Manuel,Hurtado and Ferran 1999 Information Processing Letters 71 221

[15]Khanban A A and Edalat A 2003 Proc.canad.conf.on Comput.geom 2011 94

[16]Spiller T P 1997 Proceedings of the IEEE 84 1719

[17]Nielson M A 2000 Quantum Computation and Quantum Information (Cambridge:Cambridge University Press)pp.558–559

[18]Mayers D 2004 Journal of the Acm 48 351

[19]Barrett M D,Chiaverini J,Schaetz T,Britton1.J,Itano W M,Jost J D, Knill E,Langer C,Leibfried D,Ozeri R and Wineland D J 2004 Nature 429 737

[20]Jennewein T,Simon C,Weihs G,Weinfurter H and Zeilinger A 2000 Phys.Rev.Lett.84 4729

[21]Bennett C H and Brassard G 1984 Proceedings of the IEEE International Conference on Computers,Systems,and Signal Processing,Bangalore,India,pp.175–179

[22]Valerio S and Renato R 2008 Phys.Rev.Lett.100 200501

[23]Yousuke S,Ryutaroh M and Tomohiko U 2010 J.Phys.A 43 495302

[24]Raymond Y Q C and Valerio S 2009 New J.Phys.11 045024

[25]Bang J Y and Berger M S 2006 Phys.Rev.D 74 345

[26]Wootters W K and Zurek W H 1982 Nature 299 802

[27]Horodecki R,Horodecki P,Horodecki M and Horodecki K 2007 Rev. Mod.Phys.81 865

[28]Hines A P and Stamp P C E 2007 Phys.Rev.A 75 1004

[29]Rafaeli S 2003 Acm Computing Surveys 35 309

[30]Ye L,Yao C and Guo G 2001 Chin.Phys.10 1001

[31]Riebe M,Haffner H,Roos C F,Hansel W,Benhelm J,Lancaster G P T,Korber T W,Becher C,Schmidt-Kaler F,James D F V and Blatt R 2004 Nature 429 734

[32]Pakniat R,Tavassoly M K and Zandi M H 2016 Chin.Phys.B 25 100303

[33]Weedbrook C,Pirandola S,Garcia-Patron R,Cerf N J,Ralph T C, Shapiro J H and Seth L 2011 Rev.Mod.Phys.84 621

[34]Ma H X,Bao W S,Li H W and Zhou C 2016 Chin.Phys.B 25 080309

22 February 2017;revised manuscript

15 May 2017;published online 18 July 2017)

10.1088/1674-1056/26/9/090302

∗Project supported by the National Natural Science Foundation of China(Grant Nos.61379153 and 61572529).

†Corresponding author.E-mail:yingguo@csu.edu.cn

‡Corresponding author.E-mail:duan.huang@foxmail.com

©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn