Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components∗
2017-08-30PengchengZhao赵朋程andLixinGuo郭立新
Pengcheng Zhao(赵朋程)and Lixin Guo(郭立新)
School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China
Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components∗
Pengcheng Zhao(赵朋程)†and Lixin Guo(郭立新)‡
School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China
The air breakdown is easily caused by the high-power microwave,which can have two mutually orthogonal and heterophase electric field components.For this case,the electron momentum conservation equation is employed to deduce the electric field power and effective electric field for heating electrons.Then the formula of the electric field power is introduced into the global model to simulate the air breakdown.The breakdown prediction from the global model agrees well with the experimental data.Simulation results show that the electron temperature is sensitive to the phase difference between the two electron field components,while the latter can affect obviously the growth of the electron density at low electron temperature amplitudes.The ionization of nitrogen and oxygen induces the growth of electron density,and the density loss due to the dissociative attachment and dissociative recombination is obvious only at low electron temperatures.
high power microwave,air breakdown,effective electric field,global model
1.Introduction
The high-power microwave easily causes the air breakdown because of its strong electric field.[1–5]The air breakdown is involved in many important applications,such as high power microwave systems,biomedical applications,and surface treatments.[6]In order to improve these applications,we must master the characteristics of the air breakdown,which include the breakdown formation time,breakdown electric field, breakdown plasma dynamics and pattern,and the microwave transmission in the breakdown plasma.
In recent years,many scholars have studied the air breakdown caused by the high-power microwave.[7–10]Nam et al.introduced the pressure-independent enhanced electron energy distribution function into the global model,and improved fidelity for modeling the gas breakdown.[7]The two dimensional model coupling Maxwell equations with plasma fluid equations was developed by Boeuf et al.to simulate the patterns of breakdown plasma,in which the accurate diffusion coefficient was adopted.[8]Ford et al.used the finite difference time-domain method to solve a one-dimensional model similar to that of Boeuf et al.,and predicted the breakdown formation time and the microwave transmission in the breakdown plasma.[9]The Poisson and Boltzmann equations were utilized by Zhu et al.to describe the air breakdown near the dielectric window,and the results showed that the range can be roughly divided into at least two regions,sheath region and plasma region.[10]Most of these studies above focused on the case in which the microwave has one electric field component or two mutually orthogonal and in phase electric field components.However,the microwave with two mutually orthogonal and heterophase electric field components frequently appears in the waveguide or the near field region of the antenna.We still know little about the air breakdown caused by such microwave.
In this paper,we use the global model consisting of spatially averaged continuity equations for charged particles and an electron energy equation to describe the air breakdown due to its great advantages in speed and simplicity.The global model requires the knowledge of the electric field power heating the electrons.In order to study the air breakdown caused by the microwave with the two mutually orthogonal and heterophase electric field components,we deduce the corresponding electric field power from the electron momentum conservation equation.We focus on how the phase difference between the two electron field components affects the electron temperature and electron density in the breakdown process. The dependence of the electron density on the reaction sets of oxygen and nitrogen is considered.In addition,the breakdown prediction from the global model is compared with the previous experimental data.
2.Global model
2.1.Basic equations
The global model consists of spatially averaged continuity equations for electron,and O−,and an electron energy equation.[7]When the background gas is air,theseequations can be written as

where ne,nN2,and nO2are the electron,N2,and O2densities,and nO−are theand O−densities,Teis the electron temperaturewhere ε is the electron energy and f(ε)is the normalized electron energy distribution function,εtiand Ki(i=N2–N25 in Table 1 and O2–O15 in Table 2)are the threshold energy and reaction coefficient of the reactions in Tables 1 and 2,is the energy transfer rate coefficient in the dissociative attachment collision process,PEis the electric field power for heating the electrons.

Table 1.Oxygen reaction set,εt is the threshold energy.[11]

Table 2.Nitrogen reaction set,εt is the threshold energy.[12]
These rate coefficients can be obtained by integrating the corresponding collision cross section over the electron energy distribution function.For example,the rate coefficient for the ionization of oxygen can be obtained as

where meis the electron mass,and σO14is the collision ion-ization cross section in oxygen.The detailed definition of these rate coefficients can refer to the work of Nam et al.[7]The electron energy distribution function is obtained from the Boltzmann equation solver Bolsig+at the low Te,[13],and is assumed as the Maxwellian distribution at the high Te.Next we deduce the electric field power of the microwave with the two mutually orthogonal and heterophase electric field components.
2.2.Electric field power
The two mutually orthogonal and heterophase electric field components of the microwave in time are written as

where Exmand Eymare the electron field amplitudes in xand y-axis direction,respectively,ω is the microwave angular frequency,and Δφ is the phase difference between the two electron field components.When ignoring the magnetic field force,which is much smaller than the electric field force,the electron momentum conservation equation can be written as
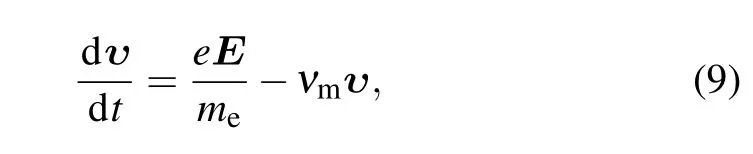
where e is the electron charge,and νmis the momentum transfer collision frequency whose definition is similar to Kiabove. By using Eqs.(7)–(9),the electron velocity is solved as

Then the electric field power is obtained as

Utilizing Eq.(13),we can deduce the average electricfield power as follows:

where〈〉denotes the time average operation.It can be found from Eq.(14)that PEadoes not depend on Δφ.By comparing PEain Eq.(14)with that of the dc electric field,[14]the effective electric field of the microwave can be defined as

By introducing the effective electric field into the empirical formulas for the ionization rate,one can easily estimate the breakdown formation time and threshold.[15]However,to obtain more physical characters,we introduce PEof Eq.(13)into the global model to simulate the air breakdown in this paper.
In order to well understand the following results,we can further simplify Eq.(13).At intermediate and high pressures, νm≫ω.Let Exm=Eym=Em,equation(13)is simplified as follows:

It can be found from Eq.(16)that PEdepends obviously on Δφ.
3.Results and discussion
When using the global model to simulate the air breakdown,the initial conditions are taken as follows:ne= 106m−3,nN+2=7.8×105m−3,nO+2=2×105m−3,and nO−=2×104m−3.In this case,the electric neutrality holds in the air at the initial time.We assume that the air is composed of 20%oxygen and 80%nitrogen since the amounts of other gases are very small in the air.The dependence of the air number density on the pressure is nair(m−3)=p(Torr)/760× 2.44×1025.
Since the oscillation frequency of PEis two times larger than that of the electric field(see Eq.(16)),we can consider the case of 0≤Δφ≤π.Figure 1 shows the variation of electron temperature and density with time at P=760 Torr, f=2.85 GHz,Exm=Eym=2.5 MV/m,and different Δφ.The electric field components of the incident microwave in time can refer to Eqs.(7)and(8).We see from Fig.1(a)that the electron temperature oscillates with time,and its oscillation frequency is two times larger than that of the electric field.It can be found from Eq.(16)that the electric field power PEcan reach the maximum when Δφ=kπ(k=0,±π,±2π,...). Therefore,among the four electron temperature amplitudes corresponding to different Δφ,the one at Δφ=0 is maximum, as shown in Fig.1(a).At Δφ=π/2,PEcan be approximated as constant(see Eq.(16)),and therefore the electron temperature Teremains almost unchanged with time.In this case, the electron temperature amplitude is minimum.At other Δφ such as 0.25π and 0.75π,the electron temperature amplitude lies between the maximum and the minimum.
We see from Fig.1(b)that the phase difference Δφ plays an important role in the electron density growth since the former affects the electron temperature obviously.At the high pressure,the electron temperature is low,and the ionization occurs only at the electron temperatures higher than the critical value.At the larger electron temperature amplitude,the ionization rate is larger and the time of electron density growth over one temperature period is longer.Therefore,the larger the electron temperature amplitude is,the faster the electron density grows.It can also be expected that the electron density growth is fastest at Δφ=0,as shown in Fig.1(b).We see from Fig.1(b)that the growth rate of the electron density is close to a constant at Δφ=π/2.This is due to the fact that the electron temperature remains almost unchanged with time.

Fig.1.(color online)(a)Variation of electron temperature with time. (b)Variation of electron density with time.P=760 Torr,f=2.85 GHz, Exm=Eym=2.5 MV/m,and Δφ=0,0.25π,0.5π,0.75π.
Figure 2 shows the variation of electron temperature and density with time at P=76 Torr,f=2.85 GHz,Exm=Eym= 2.5 MV/m,and different Δφ.At 76 Torr,the electron temperature amplitude is higher than that at 760 Torr.This is due to the increase in the collision interval during which the electrons are accelerated by the microwave and can gain energy.The effect of Δφ on the electron temperature at 76 Torr is similar to the case of 760 Torr.However,the difference among the electron densities corresponding to different Δφ is small.This can be attributed to the fact that the average electric field powers in Eq.(14)for different Δφ are the same,and with high electron temperature amplitudes,the reaction rate coefficients are not sensitive to the electron temperature oscillation.

Fig.2.(color online)(a)Variation of electron temperature with time. (b)Variation of electron density with time.P=76 Torr,f=2.85 GHz, Exm=Eym=2.5 MV/m,and Δφ=0,0.25π,0.5π,0.75π.
Figure 3 shows the breakdown formation time tbas a function of air pressure at f=2.85 GHz,Exm=Eym= 2.5 MV/m,and Δφ=0,0.25π,0.5π,0.75π.The breakdown formation time is defined as the time in which the electron density reaches 108times the initial density.[16]From the analysis of Figs.1 and 2,it can be expected that at high pressures,the phase difference Δφ has an obvious impact on the breakdown formation time tband as the pressure decreases the impact becomes small,as shown in Fig.3.In Fig.4,corresponding to the case of Fig.3,the effective electric field(see Eq.(15)) normalized to the pressure is shown as a function of P·tb(the pressure times the breakdown formation time).The simulation results show the same trend as that in the experiment of Foster et al.[17]

Fig.3.(color online)Breakdown formation time t b as a function of air pressure at f=2.85 GHz,Exm=Eym=2.5 MV/m,and Δφ=0,0.25π, 0.5π,0.75π.

Fig.4.(color online)Effective electric field normalized to the air pressure E eff/P vs.P·t b at f=2.85 GHz,Exm=Eym=2.5 MV/m,and Δφ=0,0.25π,0.5π,0.75π.

Fig.5.(color online)Reaction rates as a function of pressure when the electron density reaches 108 times the initial density.f=2.85 GHz, Exm=Eym=2.5 MV/m,and Δφ=0.5π.
It can be seen from Eq.(1)and Tables 1 and 2 that the variation of the electron density with time is related to the ionization of nitrogen(N25),ionization of oxygen(O14),dissociative attachment in oxygen(O9),dissociative recombination in oxygen(O16),electron impact detachment(O17), and detachment in oxygen(O19).Figure 5 shows how these reaction sets affect the variation of the electron density at f=2.85 GHz,Exm=Eym=2.5 MV/m,and Δφ=0.5π.It is clear that the ionization of nitrogen and oxygen causes the growth of the electron density.At low and moderate pressures,the ionization rate of oxygen is lower than that of nitrogen,since the oxygen number density is smaller than that of nitrogen.However,at high pressures,the ionization rate of oxygen is close to or higher than that of nitrogen.This is because Teis low,and then the tail of the electron energy distribution locates in the low energy region,which causes higher oxygen ionization due to its lower ionization threshold energy (12.06 eV for oxygen and 15.6 eV for nitrogen).We also see from Fig.5 that the electron density loss due to the dissociative attachment and dissociative recombination is obvious only at high air pressures.The results similar to Fig.5 can also be observed at other Δφ.
4.Conclusion
When the microwave has two mutually orthogonal and heterophase electric field components,the electron momentum conservation equation is employed to deduce its electric field power and effective electric field for heating electrons.The formula of electric field power,which depends obviously on the phase difference between the electric field components,is introduced into the global model to simulate the air breakdown caused by the microwave.The breakdown prediction from the global model agrees well with the previous experimental data. The simulation results show that the electron temperature oscillates with time,and its amplitude depends obviously on the phase difference between the two electric field components. The phase difference has an important impact on the time evolution of the electron density at low electron temperature amplitudes,and as the amplitudes increases,this impact becomes small.This can be attributed to the fact that the average electric field powers for different phase differences are the same, and with high electron temperature amplitudes,the reaction rate coefficients are not sensitive to the electron temperature oscillation.In addition,we find that the ionization of nitrogen and oxygen induces the growth of electron density,and the density loss due to the dissociative attachment and dissociative recombination is obvious only at high air pressures.
[1]Krile J T,Mcquage L,Edmiston G F,Walter J and Neuber A A 2009 IEEE Trans.Plasma Sci.2009 37 2139
[2]Cook A M,Hummelt J S,Shapiro M A and Temkin R J 2013 Phys. Plasmas 20 043507
[3]Zhao P,Guo L and Shu P 2017 Chin.Phys.B 26 029201
[4]Zhou Q H,Sun H F,Dong Z W and Zhou H J 2015 Acta Phys.Sin.64 0175202(in Chinese)
[5]Zhao P,Guo L and Li H 2015 Chin.Phys.B 24 105102
[6]Oda Y,Komurasaki K and Takahashi K 2006 J.Appl.Phys.100 113307
[7]Nam S K and Verboncoeur J P 2009 Comput.Phys.Comm.180 628
[8]Boeuf J P,Chaudhury B and Zhu G Q 2010 Phys.Rev.Lett.104 015002
[9]Ford P J,Beeson S R,Krompholz H G and Neuber A A 2012 Phys. Plasmas 19 073503
[10]Zhu M,Chang C,Yan K,Liu C and Chen C 2015 IEEE Trans.Plasma Sci.43 1670
[11]Vahedi V and Surendra M 1995 Comput.Phys.Comm.87 179
[12]The Siglo Data Base,CPAT and Kinema Software, http://www.csn.net/siglo,1998
[13]Hagelaar G J M and Pitchford L C 2005 Plasma Sources Sci.Technol. 14 722
[14]Khodataev K V 2013 Tech.Phys.58 294
[15]Ali A W 1988 Laser and Particle Beams 6 105
[16]Nam S K and Verboncoeur J P 2008 Appl.Phys.Lett.92 231502
[17]Foster J,Edmiston G,Thomas M and Neuber A 2008 Rev.Sci.Instrum. 79 114701
6 March 2017;revised manuscript
13 April 2017;published online 18 July 2017)
10.1088/1674-1056/26/9/099201
∗Project supported by the National Natural Science Foundation of China(Grant Nos.61501358,61431010,and 61627901)and the Fundamental Research Funds for the Central Universities,China.
†Corresponding author.E-mail:pczhao@xidian.edu.cn
‡Corresponding author.E-mail:lxguo@xidian.edu.cn
©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
杂志排行
Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction∗
- Collective motion of active particles in environmental noise∗
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks∗
- Analysis of dynamic features in intersecting pedestrian flows∗
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement∗
- Gas-sensor property of single-molecule device:F2 adsorbing effect∗
