First-principles study of solute diffusion in Ni3Al∗

Shaohua Liu(刘少华),Zi Li(李孜),and Chongyu Wang(王崇愚)

1 School of Materials Science and Engineering,Tsinghua University,Beijing 100084,China

2 Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

3 Department of Physics,Tsinghua University,Beijing 100084,China

First-principles study of solute diffusion in Ni3Al∗

Shaohua Liu(刘少华)1,Zi Li(李孜)2,and Chongyu Wang(王崇愚)3,†

1 School of Materials Science and Engineering,Tsinghua University,Beijing 100084,China

2 Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

3 Department of Physics,Tsinghua University,Beijing 100084,China

Using first-principles calculations in combination with Wagner–Schottky and kinetic Monte Carlo methods,the diffusion behaviors of solutes via various vacancy-mediated diffusion mechanisms in L12γ′-Ni3Al were investigated.The formation energies of the point defects and the migration energies for solutes were calculated.Adding alloying elements can decrease the defect-formation energies of NiAl,increase the defect-formation energies of AlNi,and have little effect on the formation energy of VNi.The migration energies of solutes are related with the site preference and the diffusion mechanism.The diffusion coefficients of Ni,Al,and solutes were calculated,and the concentration of antisite defects plays a crucial role in the elemental diffusion.

nickel-based superalloy,diffusion,Ni3Al,first-principles

1.Introduction

γ′-Ni3Al(L12structure)intermetallic compounds as the key strengthening precipitates of nickel-based single-crystal superalloys play a decisive role in the excellent mechanical properties for blade applications in jet engines and land-based gas turbines.[1,2]In addition,L12structure intermetallics have attracted a great deal of attention in recent years in connection with enormous potential structural materials for high temperature applications due to their anomalous temperature dependence of the yield stress.[3,4]To improve the mechanical properties and temperature resistance of γ′-Ni3Al,alloying elements,such as Ta,W,Re,Mo,and Cr,are often added.[5–7]In the investigation of creep and oxidation behavior at elevated temperature,diffusion plays an important role in the microstructure evolution,[8]planar deformation mechanisms,[9]and dislocation motion[10,11]for γ′precipitates.

Presently,there exist a large number of experimental works on self-diffusion and solute diffusion in model Ni3Al intermetallic compound measured in a wide temperature range.[12–21]Some of these data sets were studied using tracer techniques.[12–14]Unfortunately,direct experimental measurements on the Al self-diffusion in Ni3Al suffer from the lack of a suitable radiotracer Al.Thus,interdiffusion coefficients were measured using diffusion couples.[19,22,23]Due to the different concentrations of thermal defects(vacancies and anti-structure atoms)and sophisticated diffusion mechanisms in ordered intermetallics,the available data on the solute diffusion show a marked deviation and are often incomplete in the case of diffusion for alloying elements in ternary alloys.Therefore,a systematically theoretical investigation on the diffusion of alloying elements in ordered intermetallic compounds is important,not only from the fundamental scientific standpoint for gaining a deeper insight into the microscopic diffusion mechanisms,but also with the purpose of practical aspects for designing superior Ni-based super alloys.

In this work,we employed density functional theory (DFT)calculations to study the formation energy of point defects and migration barriers of ternary additions(Ti,Nb,Ta, Cr,Co,Mo,W,Re,Ru)in Ni3Al.In addition,several potential diffusion mechanisms were also taken into account and the diffusivity of Ni,Al,and solutes was predicted by using kinetic Monte Carlo(KMC)simulations.This also provides the knowledge for the diffusion behavior of alloying elements in other L12structure intermetallics(e.g.,Co3(Al,W)).

2.Computational methodology

Density-functional theory implementing in the Vienna ab-initio simulation package(VASP)[24]was used to investigate the vacancy formation and migration energies.All calculations were performed using the projector augmented wave method[25,26]and the generalized gradient approximation in the Perdew–Burke–Ernzerh of form(GGA-PBE).[27]The minimum plane wave energy cutoff was 350 eV.A first order Methfessel–Paxton smearing method[28]was used with a smearing width of SIGMA=0.2 eV.The convergence accuracy of the total energies of electronic self-consistency was 10−5eV.The Brillouin zone integration was performed with a 5×5×5 Monkhorst–Pack[29]k-point scheme.Fullionic relaxation was performed until the maximum Hellmann–Feynman force was lower than 0.02 eV/˚A.The vacancy formation and migration energies in the Ni–Al–M ternary systems were calculated in a 3×3×3(108 lattice sites)L12-Ni3Al supercell.

In the metal crystals,the dominant mechanism for the diffusion of matrix atoms and substitutional solutes is the vacancy mechanism.[30]Each atom moving through the crystal by this mechanism should satisfy two requirements:(i)a vacancy must exist at the first neighbor of the jumping atom,(ii) the thermal activation is sufficient to make an adjacent atom exchange with a vacancy.The exchange jump rate of atoms jumping into a particular neighboring site with the vacancy mechanism can be expressed as[30]

whereω denotes the jump rate between an atom and a vacancy,is the thermal equilibrium concentration of monovacancy in the crystal,and z is the coordination number.

Fig.1.(color online)Atomic configuration for ordered L12 Ni3Al,with possible directions of the vacancy jumps and possible types of point defects.Ni atoms occupy the face-centered sites and Al atoms locate at the corner position.The arrows show nearest-neighbor(NN)and nextnearest-neighbor(n)vacancy jumps.

In the L12-Ni3Al ordered structure as illustrated in Fig.1, each Ni atom is surrounded by eight nearest neighbor(NN)Ni atoms and four Al atoms,while each Al atom is surrounded by 12 Ni atoms.There are four types of point defects that can form in Ni3Al:VNion the Ni sublattices,VAlon the Al sublattices,AlNiantisite(anti-structure)atoms,and NiAlantisite atoms.The vacancy formation energies for Ni and Al atoms in the Ni3Al(γ′phase)were calculated using the Wagner–Schottky model[31,32]as follows:

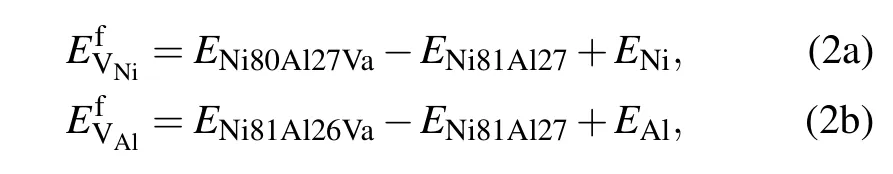
where E Ni80Al27Va,E Ni81Al26Va,and E Ni81Al27 are the energies of the supercells that contain one Ni vacancy,one Al vacancy, and no vacancy,respectively.ENiand EAlare the total energies per atom in perfect Ni and Al fcc crystals,respectively.In the presence of solute M at the Al sublattice or Ni sublattice for a dilute substitutional Ni3Al intermetallic with a vacancy, we have the expression

Based on the mean-field approximation and the mass-balance constraints,a set of non-linear equations can be determined through the minimization of the Gibbs free energy of the system(ΔG=ΔH−TΔS=min).Then,the equilibrium concentrations of point defects can be obtained by solving the following set of non-linear equations:[32]

where xiand Hidenote the mole fraction and formation enthalpy of point defect i,respectively.Note that,all calculations are performed at approximately zero pressure,the enthalpy Hiis equal to the energy Ei.xNiis the total mole fraction of Ni in the alloy.For the stoichiometric L12Ni3Al,xNi=0.75.For a given composition and temperature,the equilibrium concentrations of all point defects can be obtained by solving Eq.(4).

Based on the harmonic transition state theory (hTST),[33–36]the jump rate can be expressed as

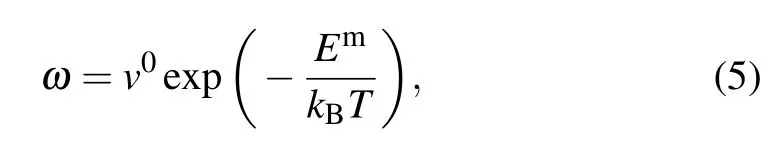
where ω is the number of jumps per unit time to a neighboring site andν0is the attempt frequency,which is of the order of the Debye frequency v0=1013Hz.Emis the migration barrier of Al,Ni,and M solutes,which is calculated using the climbing image nudged elastic band method(CI-NEB)as implemented in the VTST package[37]for VASP.Three image CI-NEB calculations were used to determine the minimum energy path. Then,the images were fully relaxed until the total energy of electronic self-consistency was below 10−5eV and the maximum Hellmann–Feynman force was below 0.02 eV/˚A.

According to the Einstein–Smoluchowski(ES) relation,[30]the coefficient of diffusion is directly related with the mean square displacement of atoms and can be written as

where〈L2〉is the total mean square displacement and τ is the simulation time in the simulation with averages taken over 105KMC trajectories.In each trajectory,105transitions are considered.

As mentioned above,the fractions of the Al and the Alsubstituting solutes on the Ni sublattice should be considered. Then,the exchange jump rate can be obtained as

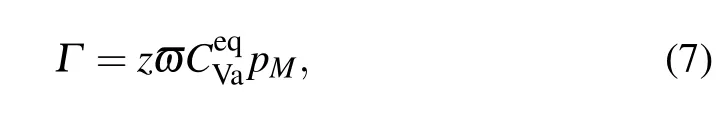
where pMdenotesthe fraction ofelementson Nisublattice.By neglecting the concentration of the Al vacancy concentration,can be written for the stoichiometric composition.

Introducing the exchange jump rate Γ into Eq.(6),we then have

where d is the jump length,with a value offor the fcc Bravais lattices.

The concentrations of point defects and the jump rate were included in the kinetic Monte Carlo(KMC)model[34,38]to calculate the diffusion rate at any particular temperature. Details of the KMC simulations can be found in our previous publication.[36]

3.Results and discussion

3.1.Concentration of point defects

The point-defect formation energies Edefectare listed in Table 1.The formation energy of AlNiis＜0 eV,indicating that it is favorable for the defect to form.The vacancy formation energies are higher than the antisite formation energies, which agrees with earlier results in the literature.[32,39]In the Ni–Al binary phase diagram,a narrow composition interval exists on both sides of the stoichiometric compositions,which are accommodated by antisite atoms(AlNiand NiAl).By numerically solving Eq.(4)with the point-defects formation energies given in Table 1,the concentrations of point defects in stoichiometric Ni3Al as a function of temperature are shown in Fig.2.Through a linear fit to the relationship

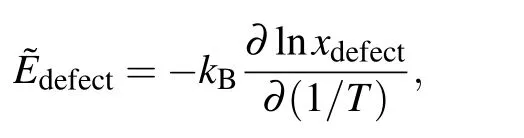
the effective defect formation energies are obtained from Fig.2 and listed in Table 2.As shown,the antisite defects are preferentially formed and vacancies are mainly formed on the Nisublattice.Note that,the defectformation energies measured by positron lifetime spectroscopy experiments should be compared with˜Edefectrather than Edefect,since the former is dependent on the alloy composition while the latter is dependent on the reference states of pure elements.As shown in Table 2,our calculations are in good agreement with the experiments.

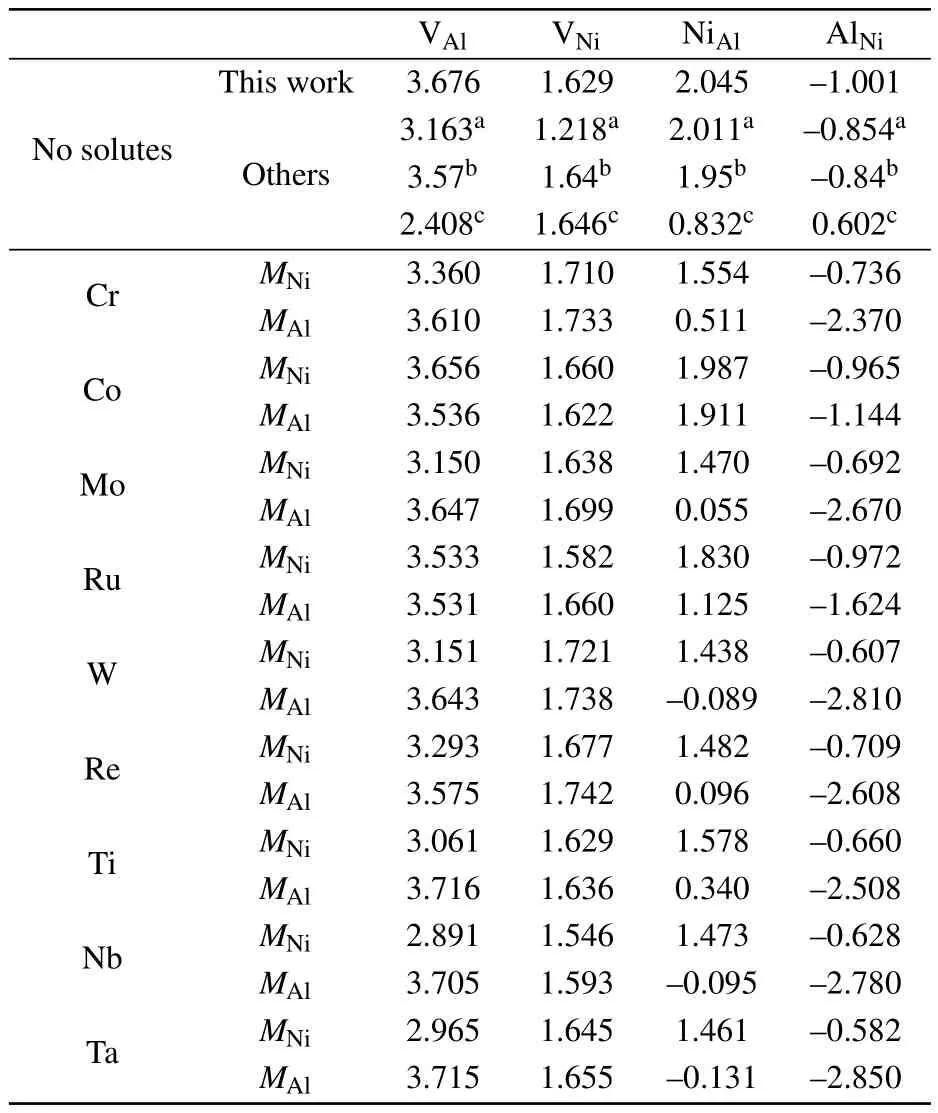
Table 1.Point defect formation energies(in units of eV)in Ni3Al with and without solutes in comparison with those from the literature.

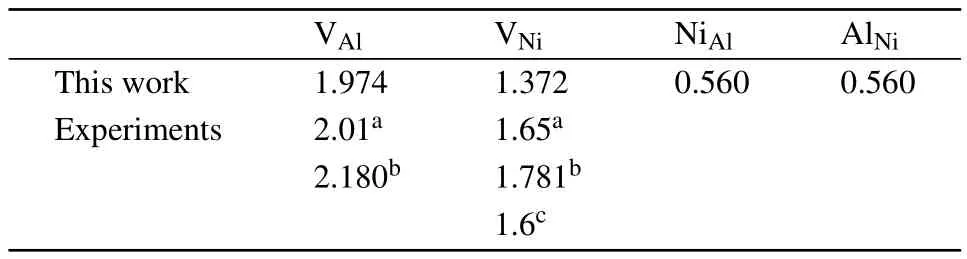
Table 2.Effective formation energies(in units of eV)of point defects in stoichiometric Ni3Al.

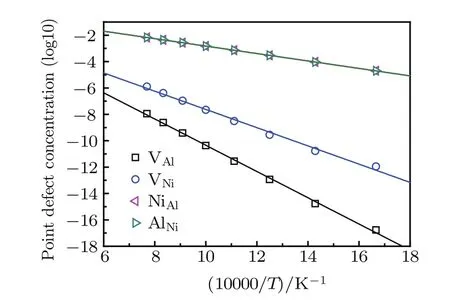
Fig.2.(color online)Equilibrium point defect concentrations in stoichiometric Ni3 Al as a function of temperature.

In multi-component super alloys,a variety of alloying elements dissolve in Ni3Al.Therefore,the solutes can influence the formation of Ni and Al vacancies and antisite atoms in Ni3Al.In order to gauge the maximum effect of the solutes on the point-defect energy,the solutes were placed in the NN positions of the point defect.Table 1 summarizes the influence of ternary solutes on formation energies of point defects.For the MNi,M is predicted to decrease the defect-formation energies of VAland NiAl,while increase that of AlNi.The effect of the solutes on the formation energy of VNiis negligible.For the MAl,the effect of the solutes on the point-defect energy is similar to that of Al,except that Ti,Nb,and Ta increase the formation energy of VAl.

It is known that vacancy-mediated diffusion is governed by the vacancy formation and vacancy-atom exchange process.The formation vacancy is a prerequisite for alloying element diffusion and the concentration of point defects may influene the diffusion rate.

3.2.Diffusion of solutes

In the L12ordered Ni3Al intermetallic compounds,certain vacancy-mediated diffusion mechanisms possibly work, such as six-jump-cycle(6JC),sublattice assisted diffusion (AS),antistructure bridge(ASB),etc.[45]The 6JC consists of six jumps and the energy barrier for the cycle is higher than the other mechanisms,[40]so the important diffusion mechanisms relevant to the diffusion behavior of Al in Ni3Al are AS and ASB jump as shown in Fig.3.The major component(Ni)of Ni3Al forms a lattice structure that enables nearest neighbor (NN)jumps through the respective sublattice without producing disorder in the L12structure.The majority component and minority component may diffuse mainly in such a Ni sublattice.As shown in Fig.3,a Ni atom can exchange with a NN vacancy on its own sublattice as the intra-sublattice jump. However,an Al atom jumps into the“wrong”sublattice(intersublattice jump)that always introduces disorder in the lattice, and continues its migration through the Ni sublattice.Since the concentration of antisite defects is higher that of Ni and Al vacancies in Ni3Al,the Al and Ni antisites play an important role in diffusion processes in L12intermetallics,which can drastically enhance the mobility at higher temperatures.[46,47]The ASB mechanism for Al atoms consists of two jumps:(i)a vacancy and an adjacent Al atom exchange their positions,(ii) an NN anti-structure AlNiatom jumps into the new vacant position on the Al sublattice.Similarly,the ABS mechanism for Ni atoms involves the exchange of a Ni vacancy with an NN anti-structure NiAlatom,and then with a regular atom on the Ni sublattice.Two Al atoms(or Ni atoms),namely,regular sublattice and antisite,participate in the ASB jump and exchange their own lattices.As the result of accomplishing the ASB jump,the vacancy can jump up to the fourth coordination shell from its initial position,resulting in a large geometrical factor and increasing its contribution to the diffusivity.The steps of the ASB jump are presented in Fig.3.Based on the available experimental data on the Al-substituting solute diffusion,Divinski et al.[12]suggested that a diffusion model of the minority component via Ni sublattice as anti-structure defects in combination with the ASB mechanism also mediates the diffusion of Al-substituting solutes.

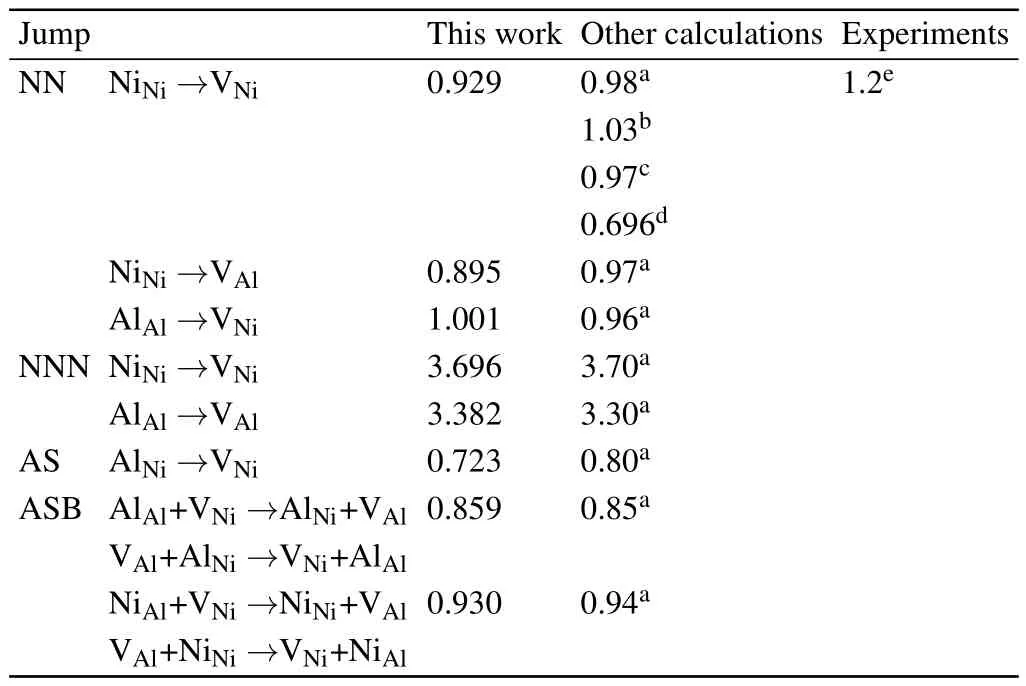
Table 3.Various energy barriers(in units of eV)for NN,n,AS,and ASB sublattice jumps for Ni and Al in L12 Ni3Al.Experimental data and previous calculations are also listed for comparison.

The calculated migration energy barrier of elementary jumps for Ni and Al in Ni3Al is listed in Table 3,which agrees well with previous calculations and available experimental values.For the NN jump,the migration energies of NiNi→VNiand NiNi→VAlare similar,with the value of∼0.9 eV.However,the n jumps for Ni and Al atoms have higher energy barriers than the NN jumps.This may be correlated with the distance of the diffusion path,the complex neighborhood environment,and the strong interactions.It indicates that the NN jump for Ni and Al atoms is energetically favorable and Al atoms will likely diffuse with the adjacent Ni vacancies.

Figures 3(b)–3(d)show the migration energies of solutes via one-step NN jump(MAl→VNi),AS jump,and ASB jump.According to our previous work about the site preference of ternary alloying additions,most metal elements exhibit a strong Al site preference in the dilute ternary ordered L12structure.[50]For the one-step NN jump,the solutes that preferentially occupy Al sites jump from the Al to the Ni sublattice,resulting in an inter-sublattice jump.From Fig.3(b), we see that the barrier energies for all solutes are higher than that for Al,which indicates that the addition of solutes into the γ′phase contributes to the inhibition of overall mass transport. In addition,all the minimum energy pathways(MEPs)for the inter-sublattice jump are asymmetric and the maximum energy appears at the position deviating from the midpoint of each step.Unlike the γ-forming elements(Cr,Co,Mo,Ru,W,Re), γ′-forming elements(Al,Ti,Nb,Ta)reach the maximum energy at a position close to the final state(MNi,endpoint structure).These resulted from the asymmetric defect structure and local atomic environment through which the vacancy passes, as shown in Fig.3(a).After the MAl→VNiinter-sublattice jumps,solutes M and Al are located at FNN positions.Because γ′-forming elements have larger atomic radii,the atomic environment around the M–Al pairs has a lattice distortion, leading to a high energy state.As shown in Table 4,the final state wherein a solute atom occupies the Ni sublattice is metastable and has a higher energy than the initial state where the solute occupies the Al sublattice.The energy difference between the final and initial states for Co is less than that for Al,while the energy increment for other solutes is higher than that for Al.It can be seen that Co atoms substitute at either an Al or Ni sublattice with a slight preference for the Al sublattice,whereas other solutes preferentially substitute at the Al sublattice.The above results agree with our previous reports about the site preference of transition metal elements in L12Ni3Al.[50]

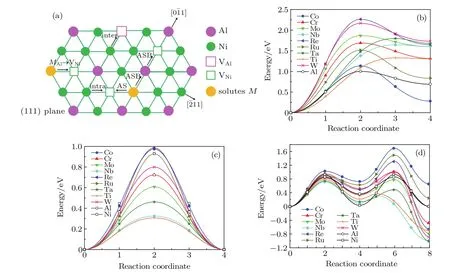
Fig.3.(color online)Diffusion pathways and minimum energy pathways for various jump mechanisms for solutes.(a)A scheme of the intra-sublattice,inter-sublattice,AS,and ASB mechanism in L12 Ni3Al.(b)Minimum energy pathways for M Al→VNi jump.(c)Minimum energy pathways for AS jump.(d)Minimum energy pathways for ASB jump.

Table 4.Energy difference(in units of eV)between the steady and the metastable states.

The schematics of the possible jump pathways and MEP plots for AS and ASB mechanisms for solutes diffusion in Ni3Al are shown in Fig.3,and the energy barriers for candidate mechanisms are listed in Table 5.For the AS mechanism, the migration energy of Re in Ni3Al with the AS mechanism is larger than that of other elements.Interestingly,the corresponding migration energy of the alloying elements for the AS jump in the ordered γ′-Ni3Al is less than that in the γ-Ni matrix,but the change in the energy barrier of Ni,Co,and Al is not much.For the ASB mechanism,the migration energy of Co is higher than that of other elements,these results may be related with the site preference of solutes in Ni3Al.Similar to the diffusion behavior of alloy elements in the matrix phase, the migration energy of the γ′-forming elements(Ti,Nb,Ta) is smaller than that of the γ-forming elements(Co,Cr,Ru,W, Re)for both AS and ASB mechanisms.However,the migration energy of Mo is lower than that of Al for AS and ASB mechanisms.

Obviously,the AS mechanism has a lower energy barrier than the other candidate mechanisms for elemental(except Co)diffusion.However,the alloying element must occupy the Ni sublattice and a Ni vacancy must occupy the NN position of the solutes for this jump to occur.These restrictions will likely result in a lower jump rate of the solute atoms compared to Ni atoms because most solutes exhibit a strong Al site preference in the ordered L12structure for multi-component superalloys. Due to Co occupying either Al or Ni sublattice in the ordered γ′-Ni3Al,the Co atoms jump from the Ni sublattice to the Al sublattice facing the competition of anti-structure AlNiatoms. Therefore,the migration energy of Co with the AS mechanism is higher than that of other solutes.In general,the stronger the preference for the Al site,the lower the energy barrier of solutes for AS and ASB mechanisms in the γ′phase.

Table 5.Calculated migration barrier(in units of eV)for various solute jumping mechanisms and site preferencein L12 Ni3Al in units of eV.

Table 5.Calculated migration barrier(in units of eV)for various solute jumping mechanisms and site preferencein L12 Ni3Al in units of eV.

a Ref.[51],b Ref.[50].

Co Ru Re Cr W Mo Ti Ta Nb M Al→VNi 1.134 1.516 2.264 1.690 2.166 1.867 1.329 1.799 1.643 AS 0.974 0.929 0.986 0.725 0.800 0.608 0.308 0.462 0.325 ASB 1.694 1.493 1.309 1.013 1.003 0.826 0.789 0.743 0.716 M in γa 1.114 1.432 1.706 1.268 1.328 1.151 0.526 0.779 0.654 Site preferenceb–0.103–0.875–1.976–1.553–2.199–2.030–1.783–2.263–2.204

As shown in Table 5,the migration energy of the ASB mechanism for solutes(except Co)is slightly higher than that of the AS mechanism,and smaller than that for MAl→VNijumps.If the concentration of the M anti-structure atoms is high enough at elevated temperature,the ASB mechanism will play a crucial role and promote elemental diffusion.This is in qualitative agreement with the previous experimental results that the higher Al self-diffusion and Al-like elements(Ge,Ga) diffusion with respect to the Ni self-diffusion occur at elevated temperature.[12]

According the theoretical works on the diffusion in Ni3Al,the Ni/Al self-diffusion and the solute diffusion are determined by the following main parameters:[12,43]the Ni vacancy concentrationthe fractions of the Al and solute M atoms at anti-structure positions(pAland pM),and the jump rates of Ni,Al,and solute atoms.Note that,both AS and ASB mechanisms are governed by the contributions of the Ni vacancy and the anti-structure defect.The latter factor pMis probably the most important one,because the vacancy formation energy of Ni for various solutes is similar as shown in Table 1.If the formation energy of the M anti-structure atom is larger than that of the Al anti-structure atoms,the probability of the ASB jumps to occur is decreased and the solute atom diffusivity is mainly determined by the MAl→VNiand AS jumps.

It is worth noting here that,the site preference of solutes in L12Ni3Al is a function of alloy composition and temperature,[52,53]and there will be a certain concentration of anti-structure atoms for solutes.Therefore,the absence of formation energy for anti-structure defects may be the reason that the activation energy of solutes obtained in the first-principles study is less than the experimental results.If the solutes occupy the Ni sublattice,the fraction of M atoms pM=1.If the solutes occupy the Al sublattice,the fraction of M atoms can be written as follows:[50,52]

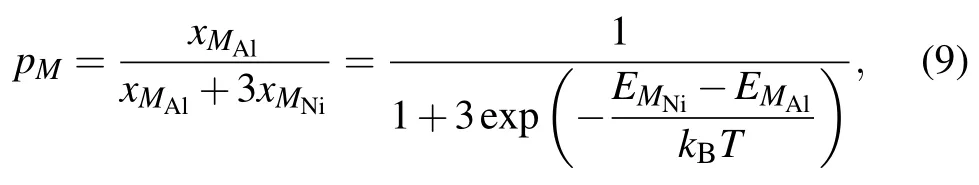
where xMAland xMAlare the concentrations of solutes on the Al and Ni sublattices,respectively.EMAland EMNiare the substitution formation energies of solutes on the Al and Ni sublattices,respectively,and the values are given in Table 5. According to Eq.(8),the diffusion coefficients of solutes via the AS mechanism are presented in Table 6.It can be seen that the diffusion coefficient of solutes is drastically reduced with the site preference from Ni to Al.The diffusion coefficients for Ni and Al with no solutes in stoichiometric Ni3Al are in good agreement with the available experimental results. The experimental results for solutes are within the range between the diffusivity for occupying Al and the diffusivity for occupying Ni,indicating that the concentration of solutes on the Ni sublattice is considerable in Ni3Al at given composition and temperature.Therefore,in addition to the migration barrier,the effect of the anti-structure defect on the diffusion of solutes is also important.Further,accurately calculating the fraction of solutes in the Ni sublattice is necessary.

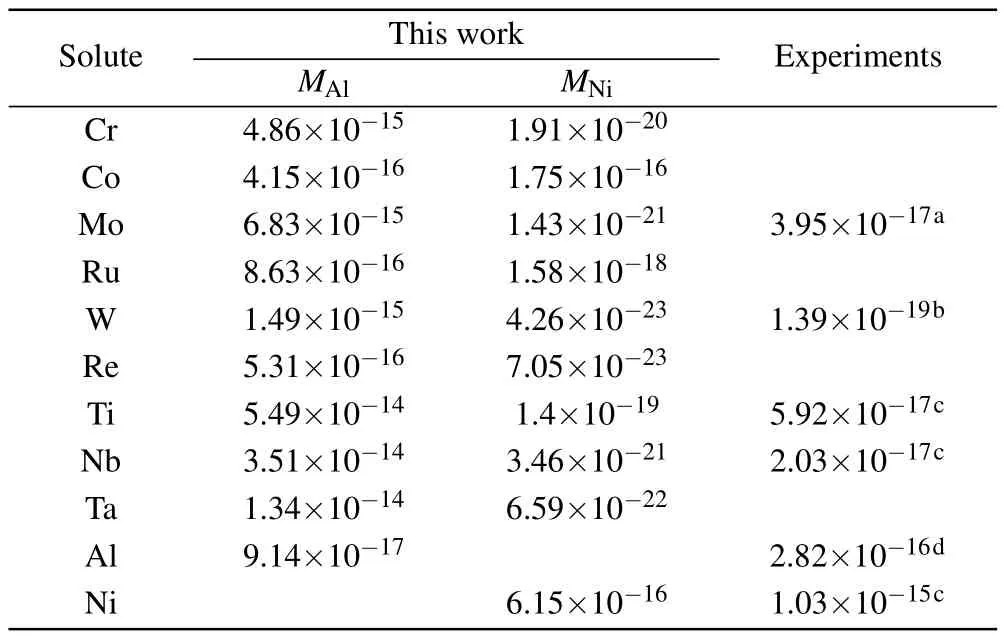
Table 6.Diffusivity(in units of m2/s)for Al,Ni,and solutes in the L12 γ′-Ni3Al phase at 1100°C in comparison with available experimental results.

4.Summary

By first-principles calculations with the KMC methods, the diffusion behavior of solutes via various vacancy-mediated diffusion mechanisms in L12γ′-Ni3Al were investigated.For the stoichiometric Ni3Al intermetallics,the AlNiand NiAlantisite atoms are preferentially formed.Vacancy formation on the Ni sublattice is energetically more favorable than on the Al sublattice.Adding alloying elements can decrease the defect formation energies of NiAland increase the defect-formation energies of AlNi.The effect of solutes on the formation energy of VNiis negligible.

The MAl→VNimechanism has a higher energy barrier than the AS and ASB mechanisms for solute(except Co)diffusion.For the MAl→VNimechanism,the barrier energies for solutes are higher than those for Al.For the AS and ASB mechanisms,the migration energy of the γ′-forming elements (Ti,Nb,Ta)is smaller than that of the γ-forming elements(Co, Cr,Ru,W,Re).The migration energy of solutes is related to the site preference of transition metal elements in L12Ni3Al.

To account for the available experimental data on the solute diffusion,various diffusion mechanisms for solutes contribute to the diffusivity in Ni3Al.The concentration of antisite defects plays a crucial role in the elemental diffusion and determines which diffusion mechanism gives the predominant contribution.

Acknowledgment

The simulations were carried out on the“Explorer 100”cluster system of the Tsinghua National Laboratory for Information Science and Technology,Beijing,China.

[1]Reed R C 2006 The Superalloys:Fundamentals and Applications(New York:Cambridge University Press)

[2]Pollock T M 2016 Nat.Mater.15 809

[3]Suzuki A,Inui H and Pollock T M 2015 Annu.Rev.Mater.Res.45 345

[4]Jiang L,Li S and Han Y 2017 IOP Conf.Ser.:Mater.Sci.Eng.182 012059

[5]Liu Z and Gao W 2001 Oxid.Met.55 481

[6]Nathal M V and Ebert L J 1985 Metall.Trans.A 16 1863

[7]Mishima Y,Ochiai S,Hamao N,Yodogawa M and Suzuki T 1986 Transactions of the Japan Institute of Metals 27 648

[8]Kamaraj M 2003 Sadhana 28 115

[9]Kovarik L,Unocic R R,Li J and Mills M J 2009 JOM 61 42

[10]Eggeler Y M,Müller J,Titus M S,Suzuki A,Pollock T M and Spiecker E 2016 Acta Mater.113 335

[11]Titus M S,Mottura A,Babu Viswanathan G,Suzuki A,Mills M J and Pollock T M 2015 Acta Mater.89 423

[12]Divinski S V,Frank S,Södervall U and Herzig C 1998 Acta Mater.46 4369

[13]Cserháti C,Szabó I A,Márton Z and Erdélyi G 2002 Intermetallics 10 887

[14]Shi Y,Frohberg G and Wever H 1995 Phys.Stat.Sol.A 152 361

[15]Fujiwara K and Horita Z 2002 Acta Mater.50 1571

[16]Cserháti C,Paul A,Kodentsov A A,van Dal M J H and van Loo F J J 2003 Intermetallics 11 291

[17]Minamino Y,Yoshida H,Jung S B,Hirao K and Yamane T 1997 Defect and Diffusion Forum 143-147 257

[18]Chen C,Zhang L,Xin J,Wang Y,Du Y,Luo F,Zhang Z,Xu T and Long J 2015 J.Alloys Compd.645 259

[19]Moniruzzaman M,Fukaya H,Murata Y,Tanaka K and Inui H 2012 Materials Transactions 53 2111

[20]Mabruri E,Sakurai S,Murata Y,Koyama T and Morinaga M 2008 Materials Transactions 49 1441

[21]Garimella N,Ode M,Ikeda M,Murakami H and Sohn Y H 2009 J. Phase Equilib.Diffus.30 246

[22]Ikeda T,Almazouzi A,Numakura H,Koiwa M,Sprengel W and Nakajima H 1998 Acta Mater.46 5369

[23]Watanabe M,Horita Z and Nemoto M 1997 Defect and Diffusion Forum 143-147 345

[24]Kresse G and Furthmüller J 1996 Phys.Rev.B 54 11169

[25]Blöchl P E 1994 Phys.Rev.B 50 17953

[26]Kresse G and Joubert D 1999 Phys.Rev.B 59 1758

[27]Perdew J P,Burke K and Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[28]Methfessel M and Paxton A T 1989 Phys.Rev.B 40 3616

[29]Monkhorst H J and Pack J D 1976 Phys.Rev.B 13 5188

[30]Mehrer H 2007 Diffusion in Solids:Fundamentals,Methods,Materials,Diffusion-Controlled Process(New York:Springer Berlin Heidelberg)

[31]Schottky W and Wagner C 1931 Zeitschr.Phys.Chem.B 11 163

[32]Jiang C,Sordelet D J and Gleeson B 2006 Acta Mater.54 1147

[33]Eyring H 1935 J.Chem.Phys.3 107

[34]Vineyard G H 1957 J.Phys.Chem.Solids 3 121

[35]Hänggi P,Talkner P and Borkovec M 1990 Rev.Mod.Phys.62 251

[36]Sun M,Li Z,Zhu G Z,Liu W Q,Liu S H and Wang C Y 2016 Commun. Comput.Phys.20 603

[37]Henkelman G,Uberuaga B P and Jónsson H 2000 J.Chem.Phys.113 9901

[38]Voter A F 2007 Radiation Effects in Solids(Dordrecht:Springer Netherlands)pp.1–23

[39]Zhang X,Deng H,Xiao S,Tang J,Deng L and Hu W 2014 J.Alloys Compd.612 361

[40]Gopal P and Srinivasan S G 2012 Phys.Rev.B 86 014112

[41]Yu S,Wang C Y,Yu T and Cai J 2007 Physica B 396 138

[42]Badura-Gergen K and Schaefer H E 1997 Phys.Rev.B 56 3032

[43]Numakura H,Ikeda T,M K and Almazouzi A 1998 Philos.Mag.A 77 887

[44]Wang T M,Shimotomai M and Doyama M 1984 J.Phys.F:Met.Phys. 14 37

[45]Gupta D 2005 Diffusion Processes in Advanced Technological Materials(Heidelberg:Springer Berlin Heidelberg)

[46]Kao C R and Chang Y A 1993 Intermetallics 1 237

[47]Divinski S V and Larikov L N 1997 J.Phys.:Condens.Matter 9 7873

[48]Chen G X,Wang D D,Zhang J M,Huo H P and Xu K W 2008 Physica B 403 3538

[49]Zhang X and Wang C Y 2009 Acta Mater.57 224

[50]Liu S H,Liu C P,Liu W Q,Zhang X N,Yan P and Wang C Y 2016 Philos.Mag.96 2204

[51]Liu S,Liu C,Ge L,Zhang X,Yu T,Yan P and Wang C 2017 Scr.Mater. Submitted

[52]Ruban A V and Skriver H L 1997 Phys.Rev.B 55 856

[53]Jiang C and Gleeson B 2006 Scr.Mater.55 433

3 June 2017;published online 18 July 2017)

10.1088/1674-1056/26/9/093102

∗Project supported by Beijing Municipality Science and Technology Commission,China(Grant No.D161100002416001)and the National Key Ramp;D Program of China(Grant No.2017YFB0701502).

†Corresponding author.E-mail:cywang@mail.tsinghua.edu.cn

©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn