基于响应面法的微操作平台可靠性稳健设计
2017-08-30胡俊峰杨展宏徐贵阳
胡俊峰, 杨展宏, 徐贵阳
(江西理工大学 机电工程学院, 江西 赣州 341000)
基于响应面法的微操作平台可靠性稳健设计
胡俊峰, 杨展宏, 徐贵阳
(江西理工大学 机电工程学院, 江西 赣州 341000)
以一种新型微操作平台为对象,考虑其结构参数的随机波动,提出一种基于6σ稳健设计思想和响应面法的可靠性稳健优化设计思路。采用筛选实验设计方法确定设计变量,采用中心组合试验设计方法建立反映平台性能指标的响应面模型。基于该模型采用一次二阶矩法得到反映平台可靠性和稳健性的性能指标,即平台位移放大倍数、固有频率和可靠性灵敏度的概率分布及可靠度。基于6σ稳健设计思想建立以平台位移放大倍数、固有频率和可靠性灵敏度的稳健性为目标,平台可靠度为约束的可靠性稳健优化模型,采用序列二次规划法对平台进行优化。将稳健优化和确定性优化结果进行比较分析可知,平台位移放大倍数、固有频率和可靠性灵敏度的方差分别减小了40.9 %、49.4 %、33.6 %,可靠度由61.36 %提高到99.78 %,实现了可靠性稳健优化的设计要求,说明了设计思路和理论模型的有效性。
微操作平台; 可靠性; 稳健设计; 响应面法; 实验设计
微操作平台广泛应用于生物工程、医疗科学、微机械制造、超精密加工、集成电路制造、扫描探针显微镜、光纤对接、光学微处理、航空航天等前沿领域[1-3]。柔顺机构是以柔性铰链代替传统运动副,利用柔性铰链的弹性变形传递或转换运动和力的一种新型机构,具有无摩擦、无间隙、分辨率高、一体化加工和免装配等优点,适宜作为微操作机器人执行机构[4-5]。
目前,国内外学者对微操作平台研究主要集中于构型设计、理论建模、力学性能的分析和优化设计[6-9],但由于平台的加工制造精度或其他随机波动因素的存在,如平台的结构参数与理想值存在偏差,平台所要求的性能指标难以得到保证。所以,如何减小结构参数的随机波动对平台性能的影响对其实际工程应用具有重要的意义。微操作平台在实际应用中对其设计和性能要求越来越高,不仅要具有微纳米级的运动精度,而且要有较大的运动空间,同时,还要具有较大的强度及快速的响应等。但这些性能均与结构参数有关,当结构参数随机变化,平台的静态性能与动态性能也会发生波动,这种波动对于要实现微纳米级操作精度的平台来说是不可忽略的,需要采用稳健设计思想以减小平台性能对噪声因素的敏感。同时,由于微操作平台是通过柔性铰链的变形传递运动和力,而且铰链的厚度较小,平台在操作过程中易发生断裂,使得平台失效。为了保证微操作平台的使用寿命,需要对平台进行可靠性稳健优化设计。
为了对微操作平台进行可靠性稳健优化设计,需要建立反映其性能与结构参数之间关系的理论模型。目前,建模方法主要为伪刚体法和有限元法。由于伪刚体法是将柔性铰链视为传统运动副建立平台的力学模型,该方法适宜于描述其静态力学性能,所建立的模型精度低。有限元法是将柔顺机构的柔性铰链和杆件划分为按一定方式相互联结的单元,具有多个自由度,该方法描述平台的力学性能具有精度高,但计算量大,计算效率低,不能得出机构参数与其性能之间的封闭形式的函数关系,不便于进行可靠性稳健优化设计。由于微操作平台结构复杂,铰链和杆件数量多,结构参数多,采用伪刚体法或有限元法均难以建立其精确的封闭形式的理论模型。响应面法是一种采用试验设计理论对指定的设计点集合进行试验,以预测非试验点的响应值的建模方法,具有计算方便,易于迭代等优点[7],所以可采用响应面方法得到平台性能参数和极限状态函数的显式表达式,以进行可靠性稳健优化设计。
本文以一种新型1维微操作平台为对象,采用响应面法建立反映平台性能的模型,基于6σ稳健设计思想,考虑平台结构参数的随机波动,以平台的位移放大倍数、固有频率性能的稳健为优化目标,以可靠度为约束,建立微操作平台多目标可靠性稳健优化数学模型,采用序列二次规划法得到稳健优化最优解,并将稳健优化结果和确定性优化进行比较分析,以说明可靠性稳健设计优化的有效性。
1 微操作平台的结构
图1为1维微操作平台,平台由4组直圆型柔性铰链和2组直梁型铰链组成的两条完全对称的运动支链组成。平台采用对称结构且通过整体加工的方式使得平台结构更为紧凑,同时由于对称结构的互补性,可以消除机构的侧向附加位移,具有较好的运动精度。平台采用两级杠杆放大原理以实现平台的大操作空间,如图1所示,杆II和直圆型柔性铰链C、D和E组成一级杠杆放大机构,其以铰链C为支点在铰链E得到一级放大;杆I和直圆型柔性铰链E、F和H组为二级杠杆放大机构。该平台具有结构紧凑、放大倍数大、固有频率和运动精度高等特点。

图1 微操作平台
微操作平台结构参数如表1所示,r,t分别表示直圆型柔性铰链半径与厚度,Lm表示杆件间的间隙,L,b分别表示杆II、III的长度和宽度,LH表示铰链H的长度;tH、tF分别表示铰链H和F的厚度,LV表示杆V的长度;LR表示减重孔之间的距离,LF表示铰链F的长度,d表示杆I的宽度,R表示减重孔的半径,h表示平台的厚度。

表1 微操作平台结构参数
2 平台可靠性稳健优化流程
6σ稳健优化设计是将可靠性设计和稳健性设计相结合的一种设计方法[10-12],当产品的性能受随机因素影响,能够通过优化实现性能指标的均值达到理想值并使其方差最小化,从而将随机变量对产品性能的影响控制在许可的范围内。所以,基于6σ稳健优化设计思想对微操作平台进行设计可以满足平台的可靠性和稳健性要求。图2描述了平台的6σ稳健优化设计思想,图中点①表示平台的确定性优化解,确定性优化为不考虑结构参数的随机变化进行优化的结果,优化过程参考文献[7]。但由于平台的加工误差会使其结构参数X在±ΔX范围内随机波动,则平台在点①处的性能指标将会有一个较大波动Δf1。为了减小性能的波动,从图2可看出,点①右边存在一个相对平缓的区域,通过对微操作平台进行稳健优化设计,得到这个区域的点②作为稳健优化解,当结构参数在相同的范围±ΔX随机波动时,此时性能指标的波动量为Δf2,由图可知,Δf2明显小于Δf1,说明点②相对于点①更为稳健,但是,点②处的性能指标的均值比点①处的均值更大。另外,点②右边为更平缓的区域,这个区域的性能指标的波动更小,但是性能指标的均值远离确定性优化解。因此,需要通过优化设计使得平台性能指标的均值最优且波动最小。
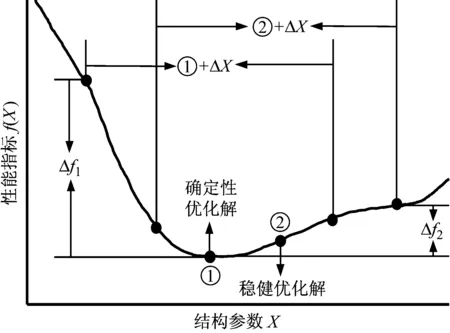
图2 平台的稳健优化设计思想
微操作平台的操作空间和动态响应速度是其性能好坏的两个重要指标,可用位移放大倍数和固有频率表征该两个指标,需要保证平台位移放大倍数和固有频率的稳健性。可靠性稳健优化流程如图3所示,首先,确定对稳健优化目标影响较大的随机波动参数,将其作为优化设计变量。然后,为了防止平台断裂失效,基于最大应力响应面模型得到平台可靠度,获得可靠性设计的指标;采用一次二阶矩法得到平台可靠性灵敏度的均值及方差,基于平台位移放大倍数和固有频率的响应面模型得到其均值及方差,得到满足稳健性的指标;最后,基于6σ稳健设计思想,以平台位移放大倍数、固有频率和可靠性灵敏度的稳健性为目标,平台的可靠度为约束,建立平台可靠性稳健优化模型。采用序列二次规划法求解优化模型,将可靠性稳健优化与确定优化结果的进行比较分析以验证可靠性稳健优化的可行性。
3 确定设计变量
由于微操作平台具有较多的结构参数,如均作为设计变量,会影响所建立的反映平台性能指标与结构参数的响应面模型的精度和优化结果的准确性。因此,需要选取对平台性能指标有较大影响的结构参数作为设计变量。筛选试验设计是一种确定因子对于响应值是否显著的试验设计方法,具有试验次数少、操作简单等优点[12-13],下面采用筛选试验设计方法筛选对平台位移放大倍数和固有频率均有显著影响的结构参数。

图3 平台可靠性稳健优化流程
筛选试验设计是2水平的部分实验设计,通过对每个因子取2水平进行分析,通过比较各个因子2水平之间的差异来确定因子的显著性。根据平台的13个结构参数范围选取2水平,即高水平(+)和低水平(-)如表2所示。根据筛选试验设计规则,对于N次试验至多可分析N-4个因子的显著性,且试验次数N为4的倍数,需3个以上虚拟变量用于估计试验误差,所以,取N为20,虚拟变量为6,试验点如表3所示,采用有限元软件ANSYS分析可得对应于各试验点的平台位移放大倍数和固有频率如表3所示。为了分析平台各结构参数对平台性能指标是否显著,根据表3所示的试验数据进行方差分析,得到各结构参数的偏回归系数、平方和、及反映显著性的概率如表4和表5所示,其中概率可表示为
Ps=P{F≤Fα(r-1,n-r)}
(1)
式中:Fα(r-1,n-r)表示在显著水平α=0.05时F(r-1,n-r)分布的临界值,r=2为水平数,n=19。由方差分析理论可知,根据Ps可确定各因子对响应是否显著性,它们的关系为
(2)
由式(2)可得各结构参数对放大倍数和固有频率的显著性分别如表4和表5所示,由表4和5可知,对平台位移放大倍数的显著因素为tH、r、t、tF、LH、d、L,对固有频率的显著因素为b、tH、r、t、tF、LH、L、LF、R。选择对放大倍数和固有频率影响均较大的结构参数为设计变量X=[x1,x2,x3,x4,x5,x6]=[tH,r,t,tF,LH,L]T,设计变量取值范围如表6所示。

表2 结构参数的2水平

表3 试验点和响应值

表4 结构参数对位移放大倍数的显著性

表5 结构参数对固有频率的显著性
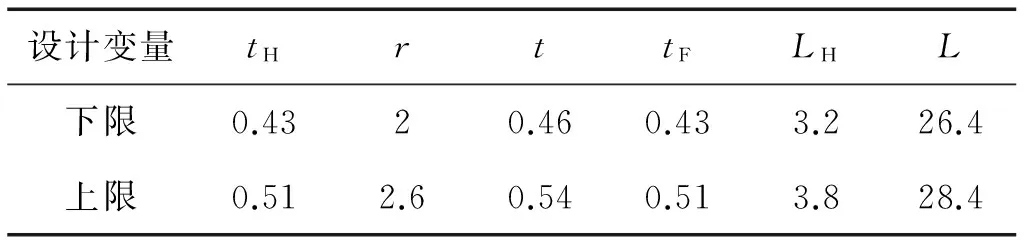
表6 设计变量取值范围
4 建立可靠性稳健优化模型
4.1 建立响应面模型
响应面法是一种采用试验设计方法对指定的设计点集合进行试验,得到目标函数和约束函数的响应面模型,以预测非试验点的响应值的方法。具有k个设计变量的二阶响应面模型为

(3)
为建立反映微操作平台的性能指标与设计变量之间关系的响应面模型,采用中心组合试验设计方法(CCD)产生试验点,由于设计变量数为6,CCD试验设计如果采用全因子试验,析因试验点较多,因此可忽略某些高阶交互效应,采用1/2分式析因设计。同时为使二阶响应面模型中的一阶项系数及交叉项系数可估,试验的分辨度应尽可能高,选用6个设计变量水平全为1的试验点作为析因设计的试验点,分辨度为VI。利用有限元得到各试验点对应的固有频率、位移放大倍数和最大应力的响应值,并根据试验点和响应值进行回归分析建立平台的固有频率、放大倍数和最大应力二阶多项式响应面模型分别为

(4)
A(X)=9.34-3.57tH-0.3r-2.88t-2.16tF+ 3.92×10-3LH+0.14L-0.7r·LH+ 0.25r·L+0.09LH·L-0.87r2-0.02L2
(5)
σmax(X)=562.96-114.97tH+103.39r+891.99t- 622.52tF+19.66LH-42.69L- 336.88r·t+217.79r·tF+ 6.62r·L-38.54r2+0.32L2
(6)
为了评价响应面函数对响应值拟合的程度,可用评价指标复相关系数R2检验,其表达式为
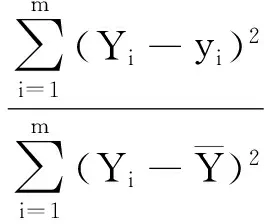
(7)
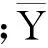
由式可计算得平台的固有频率、放大倍数和最大应力的响应面模型的评价指标如表7所示,由表7可知,3个性能指标的响应面模型评价指标R2值均接近于1,说明所建立平台的固有频率、放大倍数和最大应力的响应面模型拟合度高,能准确反映3个性能指标和设计变量之间的关系。

表7 响应面模型的评价指标
4.2 平台可靠度
由于微操作平台通过厚度小的柔性铰链传递运动和力,主要失效形式为柔性铰链由于应力集中而发生塑性变形甚至断裂。令极限状态函数为
g(X)=σmax-στ
(8)
式中,στ为材料许用应力。平台可靠度可表示为
R=P(g(X)<0)
(9)
由式(6)表示的最大应力响应面模型可得极限状态函数为
g(X)=422.96-114.97tH+103.39r+891.99t- 622.52tF+19.66LH-42.69L-336.88r·t+ 217.79r·tF+6.62r·L-38.54r2+0.32L2
(10)
为了求解平台的可靠度,采用一次二阶矩法确定g(X)的分布,将g(X)进行泰勒展开可得
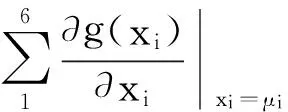
(11)
式中:Rn为余项;μi和σi(i=1,2,…6)分别为各结构参数的均值和方差。
对式(11)取数学期望,可求得极限状态函数的均值和方差的表达式分别为

(12)

(13)
综合式(12)和(13),由可靠性指标定义可得平台的可靠度指标为

(14)
则平台可靠度可表示为[14]
R=Φ(β)
(15)
式中,Φ(·)为标准正态分布函数。
4.3 平台可靠度灵敏度的均值与方差
为了保证平台可靠度的稳健性,将其可靠度对设计变量的灵敏度作为目标,使得平台的可靠度随设计变量的波动变化小。
对式(14)求偏导可得可靠度指标对各设计变量的灵敏度为
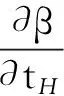
(16)

(17)

(18)

(19)

(20)

(21)
其中,
k=19.66LH-42.69L+103.39r+891.99t- 622.52tF-114.97tH+6.62Lr-336.88rt+ 217.79rtF+0.32L2-38.54r2+422.96
(22)
为了实现平台可靠度波动小,可靠性指标对每个设计变量的灵敏度均要求最小化,因此,定义可靠性灵敏度为
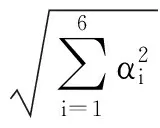
(23)
由式(16)~(23)可知,平台可靠性灵敏度为随机量,可采用均值和方差表达其特征,综合式(12)、(13)和式(23),采用一次二阶矩法可求得可靠性灵敏度的均值和方差分别为
(24)
(25)
4.4 平台性能指标均值及方差
对于微操作平台可靠性稳健设计,在保证平台可靠性稳健的同时,需要考虑结构尺寸波动对于平台性能的影响,因此,需要分别求解出位移放大倍数、固有频率的均值和方差。
对于位移放大倍数,根据式(5)表示的位移放大倍数响应面模型,采用一次二阶矩法可得其均值和方差分别为
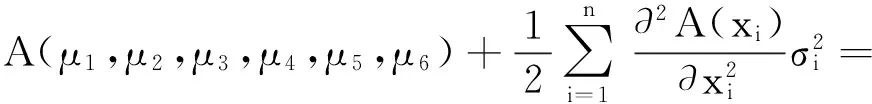
(26)

(27)
同理,可由式(4)可得固有频率的均值和方差为

(28)

(29)
4.5 可靠性稳健优化模型
对于微操作平台,位移放大倍数和固有频率分别反映了平台的操作空间和响应速度,优化目标之一是希望其均值越大越好,波动小,即其方差越小越好,以保证平台性能的稳健性。为了保证平台的可靠度,将可靠度的灵敏度的均值及方差最小作为目标之二。同时,为了满足可靠性要求,将平台可靠度作为约束。由此可知,该优化问题为属于多目标优化,根据各目标的重要性及其数量级的不同,采用目标权重系数和归一化系数将多目标优化问题归一化处理为单目标优化问题,则该可靠性稳健优化模型可表示为
minF(X)=

(30)

微操作平台的可靠性稳健优化问题属于非线性约束优化问题,采用序列二次规划法求解式表示的优化模型,目标值在优化迭代中的变化如图4所示,从该图可知,在迭代过程中,目标值逐渐变小,满足优化设计要求。
为了说明可靠性稳健优化设计的有效性,将稳健优化结果与确定性优化结果进行比较分析。由于平台采用电火花加工,加工精度较高,设平台制造允许误差Δ采用公差等级为T10,且设其结构参数服从正态分布,设计变量的初始均值为[0.51,2.6,0.5,0.52,3.3,29.4],选取各变量标准差σ=Δ/6,由标准公差表可查得在平台制造允差为T10情况下各变量标准差分别为[0.004 2,0.004 2,0.004 2,0.004 2,0.005,0.008 7]。
确定性和稳健优化结果如表8所示,从表8可看出,它们存在差别。首先比较分析平台的稳健性,分别将确定性和稳健优化结果代入式(24)~(29)分别可得位移放大倍数、固有频率和可靠性灵敏度的分布如图5所示,各指标的均值和方差如表9所示。从图5和表9可得出如下结论:① 稳健优化后的位移放大倍数、固有频率和可靠性灵敏度的方差分别减小了40.9 %、49.4 %、33.6 %,说明平台的性能波动更小,提高了其稳健性;② 固有频率均值增加了3.9 %,但位移放大倍数均值减小了7.3 %,说明稳健优化的结果与确定性优化接近,能满足平台的性能要求。然后比较分析可靠性指标,将确定性和稳健优化结果代入式(14),(15)可得平台的可靠度指标与可靠度如表10所示,由该表可知,平台可靠度由61.36 %提高到99.78 %,说明能保证平台的可靠性要求。

图4 优化目标值在优化迭代过程中的变化
Fig.4 Changes of the optimal values in the process of optimization iteration

(a)

(b)

(c)

设计变量tHrttFLHL稳健优化0.552.70.530.473.127.4确定优化0.472.30.450.413.526.2

表9 确定性优化与稳健优化的稳健性指标

表10 确定性优化与稳健优化的可靠性指标
5 结 论
以一种新型的微操作平台为对象,考虑平台结构参数的随机波动,提出一种基于6σ稳健设计思想和响应面法的可靠性稳健优化设计思路,以提高其稳健性和可靠性。建立以平台位移放大倍数、固有频率和可靠度灵敏度的稳健性为目标,以平台可靠度为约束的可靠性稳健优化模型,采用序列二次规划法求解该模型。与确定性优化相比稳健优化后的位移放大倍数、固有频率和可靠性灵敏度的方差均比确定性减小了40.9 %、49.4 %、33.6 %,平台可靠度由61.36 %提高到99.78 %,实现了可靠性稳健优化的设计要求。所提出设计思路和理论模型可用于其他微操作平台的可靠性设计。
[1] SHEN Yiping, CHEN Xuedong, JIANG Wei, et al. Spatial force-based non-prismatic beam element for static and dynamic analyses of circular flexure hinges in compliant mechanisms[J]. Precision Engineering, 2014, 38(2): 311-320.
[2] HOPKINS J B, CULPEPPER M L. A screw theory basis for quantitative and graphical design tools that define layout of actuators to minimize parasitic errors in parallel flexure systems[J]. Precision Engineering, 2010, 34: 767-776.
[3] YUE Yi, GAO Feng, ZHAO Xianchao, et al. Relationship among input-force, payload, stiffness and displacement of a 3-DOF perpendicular parallel micro-manipulator[J]. Mechanism and Machine Theory, 2010, 45: 756-771.
[4] 胡俊峰, 徐贵阳, 郝亚洲. 一种新型空间微操作平台的设计和性能[J]. 机械设计与研究, 2014, 30(1): 42-46.
HU Junfeng, XU Guiyang, HAO Yazhou. Design and characteristics of a novel spatial micro-manipulation stage[J]. Machine Design and Research, 2014, 30(1): 42-46.
[5] 胡俊峰, 徐贵阳, 郝亚洲. 基于动态特性的复合桥式微动平台优化设计[J]. 农业机械学报, 2014,45(1): 306-312.
HU Junfeng, XU Guiyang, HAO Yazhou. Optimization design of a compound bridge-type micro-platform based on dynamic characteristics[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014,45(1): 306-312.
[6] 胡俊峰, 张宪民. 3自由度精密定位平台的运动特性和优化设计[J]. 光学 精密工程, 2012,20(12): 2686-2695.
HU Junfeng, ZHANG Xianmin. Kinematical properties and optimal design of 3-DOF precision positioning stage[J]. Optics and Precision Engineering, 2012, 20(12): 2686-2695.
[7] 胡俊峰, 徐贵阳, 郝亚洲. 基于响应面法的微操作平台多目标优化[J]. 光学 精密工程, 2015,23(4): 1096-1104.
HU Junfeng, XU Guiyang, HAO Yazhou. Multi-objective optimization of micro-manipulation stage based on response surface method[J]. Optics and Precision Engineering, 2015,23(4): 1096-1104.
[8] 李春霞, 赖磊捷, 朱利民. 三自由度θXθYZ柔性机构的柔度分析与计算[J]. 工程力学, 2014, 31(8): 204-208.
LI Chunxia, LAI Leijie, ZHU Limin. Compliance analysis and calculation ofθXθYZcompliant mechanism[J]. Engineering Mechanics, 2014, 31(8): 204-208
[9] 邱丽芳, 韦志鸿, 俞必强 等. LET柔性铰链的等效刚度分析及其参数优化[J]. 工程力学, 2014, 31(1): 188-192.
QIU Lifang, WEI Zhihong, YU Biqiang, et al. Analysis of equivalent stiffness and parameter optimization of LET flexure hinge[J]. Engineering Mechanics, 2014, 31(1): 188-192.
[10] 邱继伟, 张瑞军, 丛东升 等. 机械零件可靠性设计理论与方法研究[J]. 工程设计学报, 2011, 18(6): 401-406.
QIU Jiwei, ZHANG Ruijun, CONG Dongsheng, et al. Theory and method research of mechanical components reliability design[J]. Journal of Engineering Design, 2011, 18(6): 401-406.
[11] 张瑞军, 邱继伟, 王晓伟 等. 基于多目标非耦合优化策略的可靠性稳健优化设计[J]. 中国机械工程, 2014, 25(2): 246-251.
ZHANG Ruijun, QIU Jiwei, WANG Xiaowei, et al. Reliability-based robust optimization design based on strategy of multi-objective optimization uncoupling or decoupling[J]. Chinese Mechanical Engineering, 2014, 25(2): 246-251.
[12] 彭茂林, 杨自春, 曹跃云 等. 基于响应面法的可靠性稳健优化设计[J]. 航空动力学报, 2013, 28(8): 1784-1790.
PENG Maolin, YANG Zichun, CAO Yueyun, et al. Reliability robust design optimization based on response surface method[J]. Journal of Aerospace Power, 2013, 28(8): 1784-1790.
[13] 赵选民. 试验设计方法[M]. 北京: 科学出版社, 2006, 134-137.
[14] 牟致忠. 机械可靠性-理论·方法·应用[M]. 北京: 机械工业出版社, 2011.
Reliability-based robust design of a micro-manipulation Stage with response surface method
HU Junfeng, YANG Zhanhong, XU Guiyang
(School of Mechanical & Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)
A novel micro-manipulation stage was taken as a design object, a reliability-based robust optimization design method was proposed based on the 6σ robust design idea and the response surface method considering random fluctuations of its structural parameters. The design variables were determined with screening tests. The response surface model reflecting the stage’s performance indexes was built with the central composite design. Based on this model, the first-order second moment method was used to obtain performance indexes to reflect the stage’s reliability and robustness, they are probability distributions of the stage’s displacement amplification factor, its natural frequencies and its reliability sensitivity and the stage’s reliability. Based on the 6σ robust design idea, the stage’s reliability-based robust optimization model was established taking robustness of the stage’s displacement magnification factor, its natural frequencies and its reliability sensitivity as the objective, and the stage’s reliability as the constraint. The sequential quadratic programming method was adopted to solve this optimization problem. Comparing the results of this robust optimization with those of the deterministic one, it was shown that the variances of the stage’s displacement magnification factor, its natural frequencies and its reliability sensitivity decrease by 40.9%, 49.4% and 33.6%, respectively; the stage’s reliability increases from 61.36 % to 99.78 %; so the proposed design meets the design requirements of reliability-based robust optimization, the effectiveness of the proposed design idea and theoretical model is verified.
micro-manipulation stage; reliability; robust design; response surface method; test design
国家自然科学基金(51265016; 51565016)
2015-12-30 修改稿收到日期:2016-06-19
胡俊峰 男, 博士,副教授,1978年生
TH122
A
10.13465/j.cnki.jvs.2017.15.037
