空间薄壁CFRP豆荚杆模态试验及分析

康雄建， 陈务军， 邱振宇， 余征跃， 谢 超， 曹争利

(1. 上海交通大学 空间结构研究中心， 上海 200030； 2. 上海交通大学 工程力学系， 上海 200240；3. 上海宇航系统 工程研究所， 上海 201108)

空间薄壁CFRP豆荚杆模态试验及分析

康雄建1， 陈务军1， 邱振宇1， 余征跃2， 谢 超3， 曹争利3

(1. 上海交通大学 空间结构研究中心， 上海 200030； 2. 上海交通大学 工程力学系， 上海 200240；3. 上海宇航系统 工程研究所， 上海 201108)

空间薄壁CFRP豆荚杆工作时处于悬臂状态，为掌握其结构动态响应，对10 m长的超长薄壳豆荚杆在下端刚接约束下进行模态试验，得到了其模态和频率。利用有限元软件ADINA对试验模型在不考虑和考虑空气的情况下进行数值模拟分析，得到其在下端刚接约束下的模态和频率。数值模拟与试验结果对比分析表明：对于该试验研究对象，沿弱轴方向的基频，不考虑和考虑空气的计算结果和试验的误差分别为36.4%和4.7%，因此在地面试验和数值分析的过程中需要考虑空气与结构耦合的影响。进一步对豆荚杆的杆长进行参数化分析，得到了3～10 m豆荚杆的基频在不考虑空气和考虑空气影响下的偏差。对悬臂薄壁CFRP豆荚杆的设计、应用具有重要参考价值。

空间薄壁CFRP豆荚杆； 模态试验； 流固耦合； 数值模拟

可缠绕-伸展的悬臂薄壁CFRP豆荚杆具有轻质、收展原理简单、收纳率高、可重复性强和精度高等特点，常用作太阳帆、空间薄膜天线阵面等可收展的航天器的支撑体系构件[1]。为掌握其结构受力特性等性能，国内外一大批学者进行了相关研究。

在国内，白江波等[2]对可折叠、自动展开复合材料豆荚杆的设计、制备展开研究，并进行了相关验证。房光强等[3]对豆荚杆的结构、材料进行了优化设计，并对多种不同材料的豆荚杆试件进行性能测试与评估。董志强等[4]根据豆荚杆展开和收拢过程中的受力情况，采用变尺寸设计对豆荚杆进行优 化设计。李瑞雄等[5-8]对薄壁CFRP豆荚杆的拉扁、 压扁、缠绕和展开过程进行了较为深入系统地研究，并进行豆荚杆轴压屈曲分析和模态分析。刘锦贤等[9]对豆荚杆在工作状态下的热效应进行了数值模拟分析和试验研究。

在国外，Herbeck等[10]对复合材料薄壁豆荚杆的制造工艺、屈曲模式、面内刚度进行了研究。Sickinger等[11]对复合材料薄壁豆荚杆在轴向压缩、组合弯矩作用下结构的屈曲失效的包络图进行研究。Irwin等[12]对复合材料薄壁豆荚杆的设计、制造、评估进行了研究，并通过四点纯弯试验分析了豆荚杆纯弯结构响应。Chu等[13]对复合材料薄壁豆荚杆的设计理论和展开后的结构动态响应进行了研究。Straubel等[14]在失重条件下对豆荚杆展开过程进行试验研究。

CFRP薄壁豆荚杆在轨处于热交变真空环境，但在地面验证试验和动力学测试中，豆荚杆处于空气环境。长细比较大的豆荚杆，其轻质、刚度小、柔度大，空气对豆荚杆振动影响显著，即常规模态测试辨识(空气环境)和模态分析(无空气作用)结果差异大，这给验证测试方法、技术指标论证、动力分析等带来问题。未见相关研究工作报道。

本文针对细长柔性豆荚杆悬臂模态试验，提出考虑流固耦合的模态分析识别方法，并进行参数分析。

1 薄壁CFRP豆荚杆模态试验

本试验的主要目的是为了得到薄壁CFRP豆荚杆在下端固定状态下沿两个对称轴方向的固有频率和模态。豆荚杆长度为10 000 mm，截面如图1，截面由中间圆弧段、两边圆弧段和两边直线段组成，截面尺寸为240 mm×120 mm，截面面积为200.25 mm2，回转半径ix、iy分别为67.15 mm 和35.90 mm，由上下两肋片两边黏合而成，薄壁对称透镜状。中间段圆弧采用由7层碳纤维增强环氧树脂预浸料铺成，每层厚度为0.060 mm，铺设角度为：[+45/0/-45/0/-45/0/+45]；两边圆弧段和两边直线段采用由5层碳纤维增强环氧树脂预浸料铺成，每层厚度为0.060 mm，铺设角度为：[+45/-45/0/-45/+45]；预浸料力学性能见表1。分别以截面对称轴X轴、Y轴为中性轴进行试验，测定豆荚杆在悬臂固定状态下沿X轴、Y轴的频率、模态。试验仪器如图2，在试验过程中，豆荚杆上分布有多个测位点，在每个测位点上贴上高反射贴片，在激振器稳态激励或脉冲荷载作用下，整个结构会发生振动，当激光照射到被测点时，由于多普勒效应，入射光和反射光的频率会发生变化，控制系统软件通过分析入射光和反射光的频率变化，得到被测点的速度信号，从而得到被测结构的速度频率响应谱。当得到每个测位点的速度响应后，把这些测位点的信号连起来就得到了结构的整体模态。

表1 预浸料力学性能

图1 薄壁豆荚杆横截面(mm)

(a)控制器(b)扫描器(c)激振器

图2 试验仪器

Fig.2 Test instrument

1.1 X轴向模态试验

下端固定状态模态测试试验方案布置如图3所示，薄壁CFRP豆荚杆的下端通过螺栓与法兰连接，法兰通过压块固定在钢结构网格底座上，保证形成刚接的边界条件。法兰、薄壁管的中心应该保持在同一竖直直线上。激振器扫激振的扫描频率为0～50 Hz。

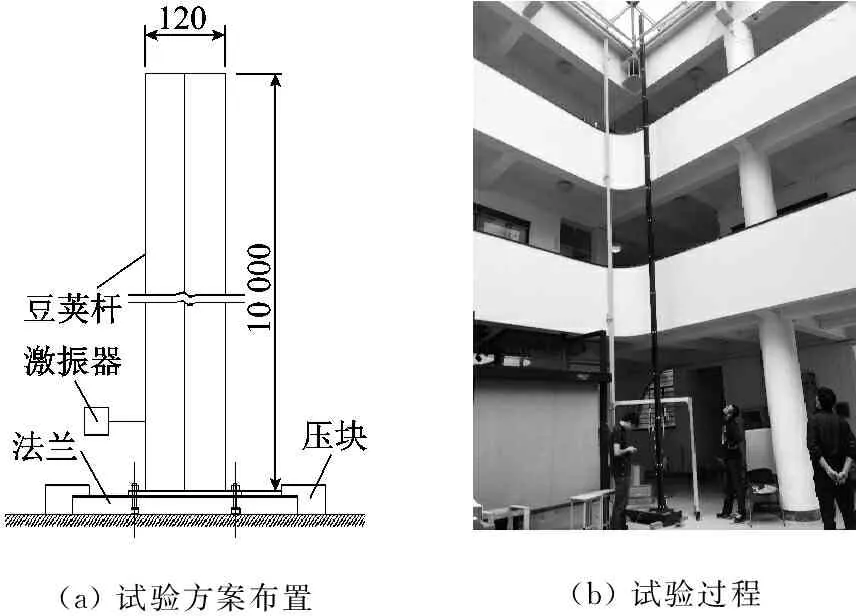
(a)试验方案布置(b)试验过程

(c) 下端刚接约束形式

(d) 激振器安装图

试验过程：

(1) 豆荚杆下端与底部法兰连接，将底部法兰固定于钢结构网格底座上；

(2) 调整扫描器的位置，使豆荚杆整体出现在控制器显示器的中央位置；

(3) 将激振器与豆荚杆靠近根部的位置黏结；

(4) 整根豆荚杆分14个测位点；

(5) 开始试验，记录数据。

(6) 拆除激振器，用手敲击豆荚杆靠近根部位置，再次记录试验数据。

试验结果：

在激振器连续激励下(0～50 Hz)，得到薄壁CFRP豆荚杆的前三阶模态如下图4所示，分别为对应第1,2,3阶弯曲，但端部有一段鞭梢效应，也是柔性的显著标志。

(a)第一阶(b)第二阶(c)第三阶

图4 豆荚杆X轴向前三阶模态

Fig.4 The first three order modal alongXaxis

激振器连续激励(0～50 Hz)以及脉冲荷载激励下(即用手敲击豆荚杆靠近根部位置)，薄壁CFRP豆荚杆沿X轴向振动频率响应曲线,如图5所示。

由图5可知，在激振器扫频激励下，频率响应谱中不仅包含了结构的固有频率，还包含了结构的呼吸模态，扭转模态以及由于结构下端和激振器黏结而引起的其他模态。激振器激励下和脉冲荷载激励下的基频分别为1.75 Hz、1.84 Hz，这是由于在有激振器存在的情况下，激振器和豆荚杆黏结在一起，相当于给了豆荚杆额外约束，因此测得的频率与实际的频率会有稍微的差异。激振器与豆荚杆端部的距离越大，误差越大，因此在试验过程中，应保证激振器尽量靠近豆荚杆端部，同时应该以脉冲荷载激励下的试验结果为准。

图5 豆荚杆X轴向频率响应谱

1.2Y轴向模态试验

Y轴向模态测试只需将豆荚杆截面转90°，激振器沿Y轴激励。试验方案布置、试验过程同1.1节。

试验结果：

在激振器连续激励下(0～50 Hz)，得到薄壁CFRP豆荚杆的前三阶模态如下图6所示，其特征类似X轴振型，但鞭梢效应更显著，第1阶非基本的第1阶弯曲，而是近顶端部1/2内呈局部半周期正弦波，第2，3振型顶端在中性轴反侧有振幅。与经典Bernoulli梁悬臂振型有较大差异。

(a)第一阶(b)第二阶(c)第三阶

图6 豆荚杆Y轴向前三阶模态

Fig.6 The first three order modal alongYaxis

激振器连续激励(0～50 Hz)以及脉冲荷载激励下(即用手敲击豆荚杆靠近根部位置)，薄壁CFRP豆荚杆沿Y轴向振动频率响应曲线，如图7所示。

由图7可知，在激振器扫频激励下，频率响应谱中不仅包含了结构的固有频率，还包含了结构的呼吸模态，扭转模态以及由于结构下端和激振器黏结而引起的其他模态。激振器激励下的基频和脉冲荷载激励下的基频分别为1.03 Hz、1.00 Hz，和X轴向振动试验一样，仍以脉冲荷载激励下的试验结果为准。沿X轴向和Y轴向振动的前三阶频率，如表2所示。

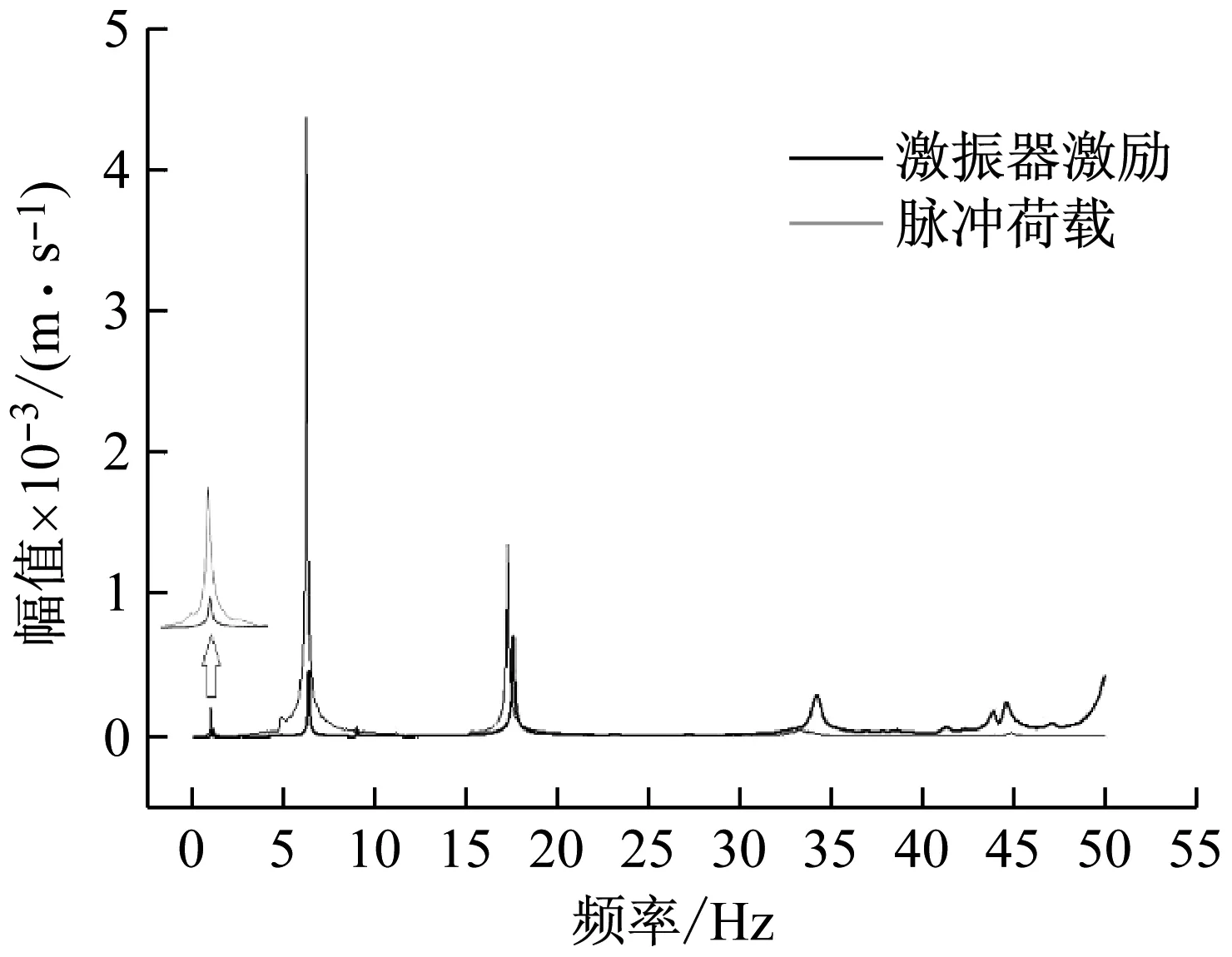
图7 豆荚杆Y轴向激振器激励下频率响应谱

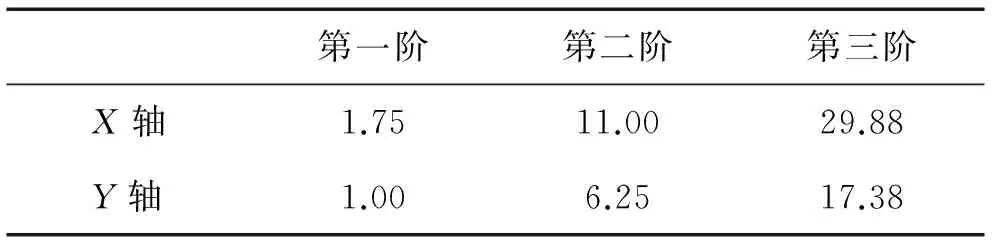
第一阶第二阶第三阶X轴1.7511.0029.88Y轴1.006.2517.38

由表2可知，豆荚杆沿X轴向的振动频率均高于对应的沿Y轴向的振动频率，这是由于豆荚杆沿X轴向的刚度大于沿Y轴向的刚度(回转半径ix、iy分别为67.15 mm 和35.90 mm，ix大于iy)。

2 薄壁CFRP豆荚杆模态数值仿真模拟

2.1 不考虑空气影响的数值仿真模拟

利用有限元软件ADINA建模分析，薄壁豆荚杆采用碳纤维复合材料铺设，尺寸和铺层如图1，在底部施加固支约束，采用四节点Shell单元，碳纤维单层材料参数如表1。有限元模型，如图8所示。

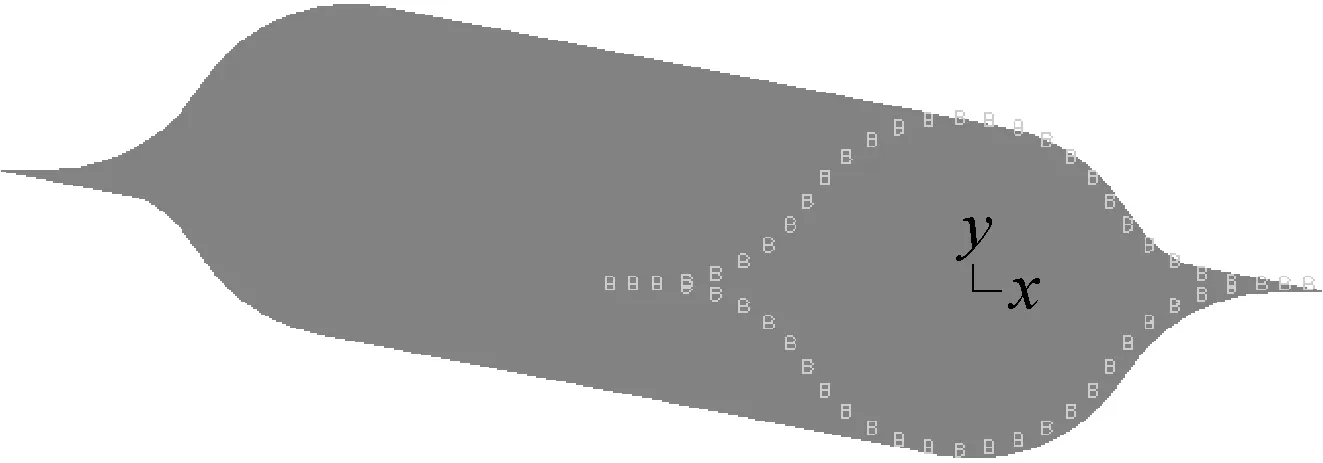
图8 豆荚杆有限元模型

进行Frequencies/Modes分析，求解器选择Lanczos Iteration。薄壁豆荚杆沿X轴、Y轴向振动的前三阶模态计算结果如图9、图10所示，其振型与模态测试辨识结果一致，但未呈现如试验明显的鞭梢效应。

数值仿真计算得到的前三阶频率，如表3所示。

将数值仿真计算结果和试验结果对比,如表4所示。

由表3，4可知，ADINA数值仿真计算与试验在沿X轴向振动的结果吻合较好，最大误差为沿X轴向的第三阶频率的，为6.96%；但在沿Y轴向的振动试验与ADINA的数值仿真有较大的误差，平均有36.53%的误差。初步分析是没有考虑空气影响的原因，将在下一节深入讨论。

(a)第一阶(b)第二阶(c)第三阶

图9 沿X轴向振动的前三阶模态

图10 沿Y轴向振动的前三阶模态

表4 数值计算结果和试验对比

2.2 考虑空气影响的数值仿真模拟

利用ADINA进行结构流固耦合分析。重新建立有限元模型。采用ADINA-M模块进行建模，分别建立薄壁豆荚杆内部流场模型和外部20 m×20 m×12 m的流场模型，流场为势流、无黏性，不可压缩流体。在耦合界面上，流体求解器将流体表面应力传递给结构求解器，作为外力施加到结构方程中；反之，结构求解器将结构边界上的位移和速度传递给流体求解器，作为求解流体方程的必要条件。用Nf和Ns分别表示流固耦合边界上的流体节点和结构节点，定义流固耦合界面上的映射算子如下：

将外部流场的body沿XZ平面切开，在外部流场生成薄壁豆荚杆的两边直线段的印记，并在所有的面上定义Face-Link,以保证相邻的面上节点一一对应。薄壁豆荚杆和内部流场区域网格划分密一些，外部流场网格划分稀疏一些。豆荚杆的材料、铺层、网格参数不变，仍采用四节点Shell单元。在内部流场的环向外表面和外部流场的由印记生成的面上划分网格。选择标况下空气的物理参数，即空气的体积模量为10 100 MPa，密度为1.29 kg/m3。流场的单元类型为8节点3D-Fluid，并选择单元内拟合，使节点不连续。在薄壁豆荚杆的底部施加固支约束，在外部流场的两个外表面上流体的势设为0。整个有限元模型，如图11所示。

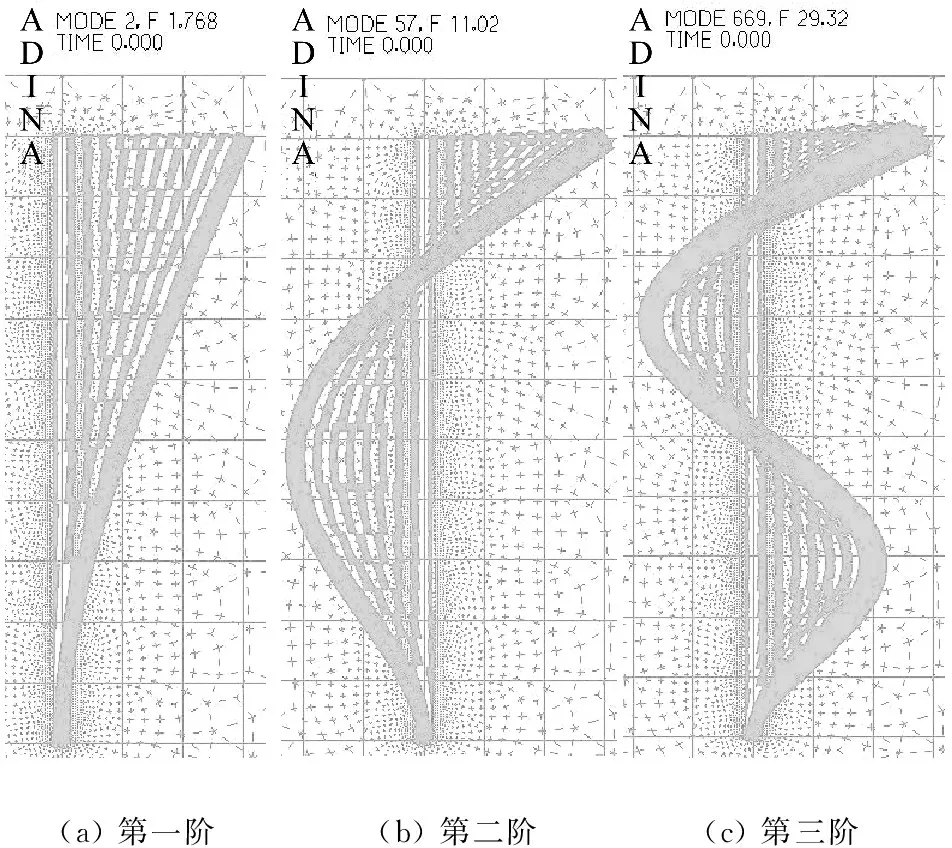
进行Frequencies/Modes分析，求解器选择Lanczos Iteration。薄壁豆荚杆沿X轴、Y轴向振动的前三阶模态计算结果如图12、图13所示，其振型总体与试验更接近，鞭梢效应明显。

考虑空气影响数值仿真计算得到的前三阶频率,如表5所示。

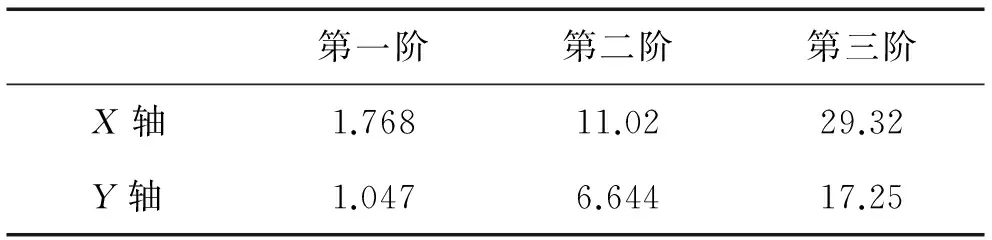
表5 数值仿真结果

图11 流固耦合有限元模型

(a)第一阶(b)第二阶(c)第三阶

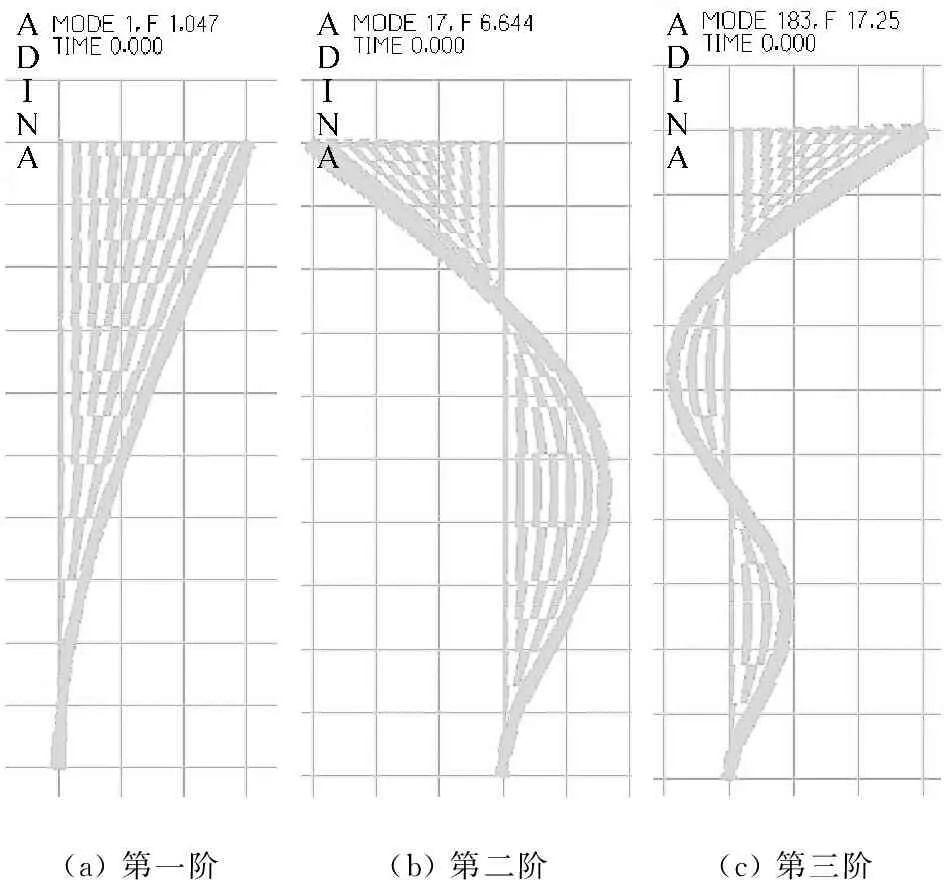
图12 沿X轴向振动的前三阶模态

图13 沿Y轴向振动的前三阶模态

Fig.13 The first three order modal alongYaxis

将试验结果、不考虑空气的数值计算结果以及考虑空气的数值计算结果对比,如表6所示。

表6 不考虑空气、考虑空气仿真结果和试验结果的对比

由表6可知，在考虑了空气影响的情况下，数值计算结果和试验结果在X轴向和Y轴向都吻合的较好。其中沿X轴最大的误差为1.87%，沿Y轴向最大的误差为6.30%；不考虑空气影响的数值计算结果和试验结果以及不考虑空气影响和考虑空气影响的数值计算结果在X轴向的差异较小，最大差异分别为6.96%、9.00%；但在Y轴向的差异较大，最大差异分别为36.77%、37.79%。造成这样结果的原因主要有两点：① 豆荚杆沿X轴向振动的截面为流线型，空气的影响较小。图14给出了豆荚杆在横截面内的压力系数分布，由此可计算出沿X轴向和Y轴向振动的空气阻力系数分别为0.147和0.521，因此空气对X轴向的影响要小于对Y轴向的影响；② 豆荚杆的回转半径ix、iy分别为67.15 mm 和35.90 mm，ix大于iy，豆荚杆沿X轴向的刚度大于沿Y轴向的刚度。因此，对于本文所研究的10 m超长薄壳豆荚杆，在试验和数值分析的过程中，需要考虑空气对结构的影响。

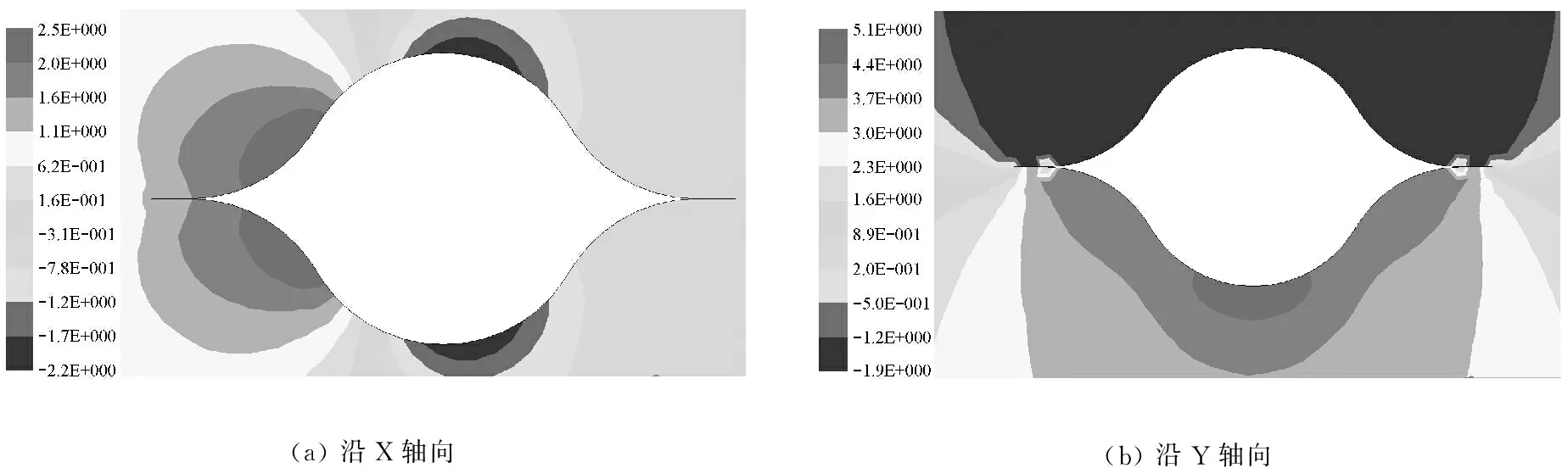
(a)沿X轴向(b)沿Y轴向

图14 沿X轴向和Y轴向振动的压力系数分布

Fig.14 Pressure coefficient distribution alongXaxis andYaxis

3 薄壁CFRP豆荚杆模态参数分析

豆荚杆与空气的接触面积与豆荚杆的长度有关，因此在其余参数不变的情况下，豆荚杆的长度为3～10 m，利用ADINA分别对不考虑空气和考虑空气情况下薄壁豆荚杆的基频进行数值计算分析，得到的结果，如下表7所示。

将不同杆长的豆荚杆在两种不同工况下的基频的偏差值作对比，如图14所示。并对Y轴向的杆长与偏差值的关系作三次多项式拟合：y=-3.68+4.20x+0.14x2-0.02x3，相关系数为0.989 43。

由以上分析可知：在考虑空气影响和不考虑空气影响两种情况下，杆长的变化对X轴的频率的偏差的影响较小，基本维持在4%左右；对于沿Y轴方向，频率的偏差的值大致随着杆长的增加而增加，在杆长为3 m的时候，考虑空气和不考虑空气的频率偏差为9.39%，在杆长为10 m的时候，为30.27%。因此，在试验过程中和实际工程应用中，要根据实际对象的不同，决定是否需要考虑空气对豆荚杆沿Y轴方向频率的影响。

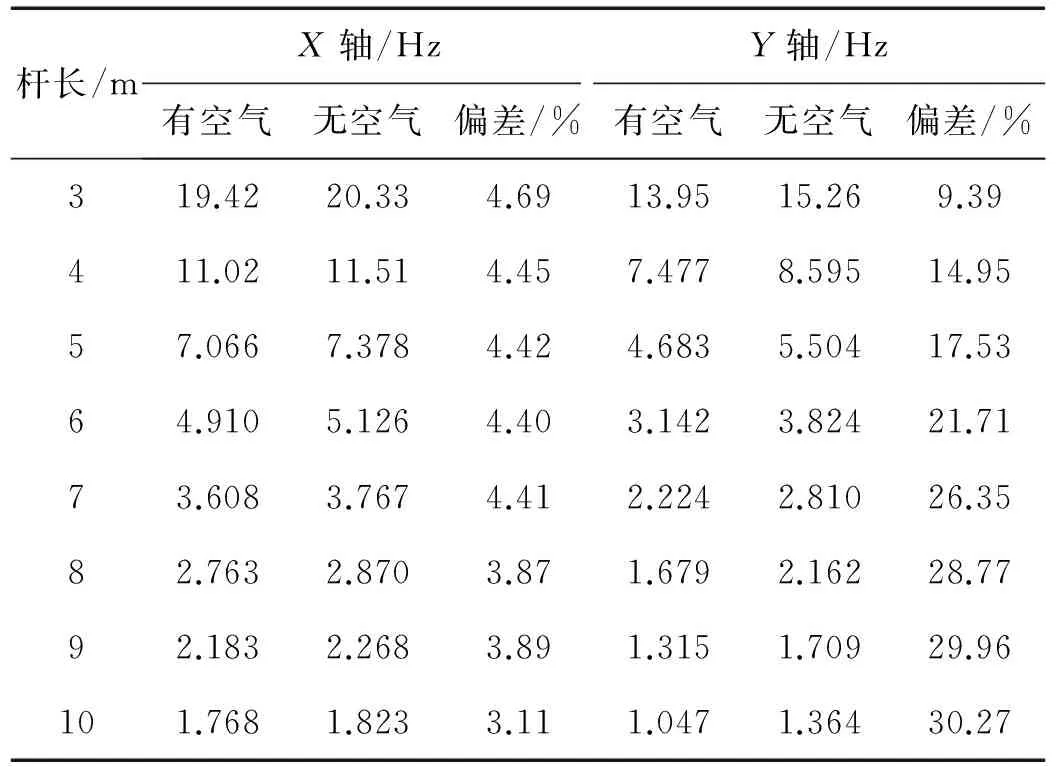
表7 不同杆长的沿X轴、Y轴的一阶频率

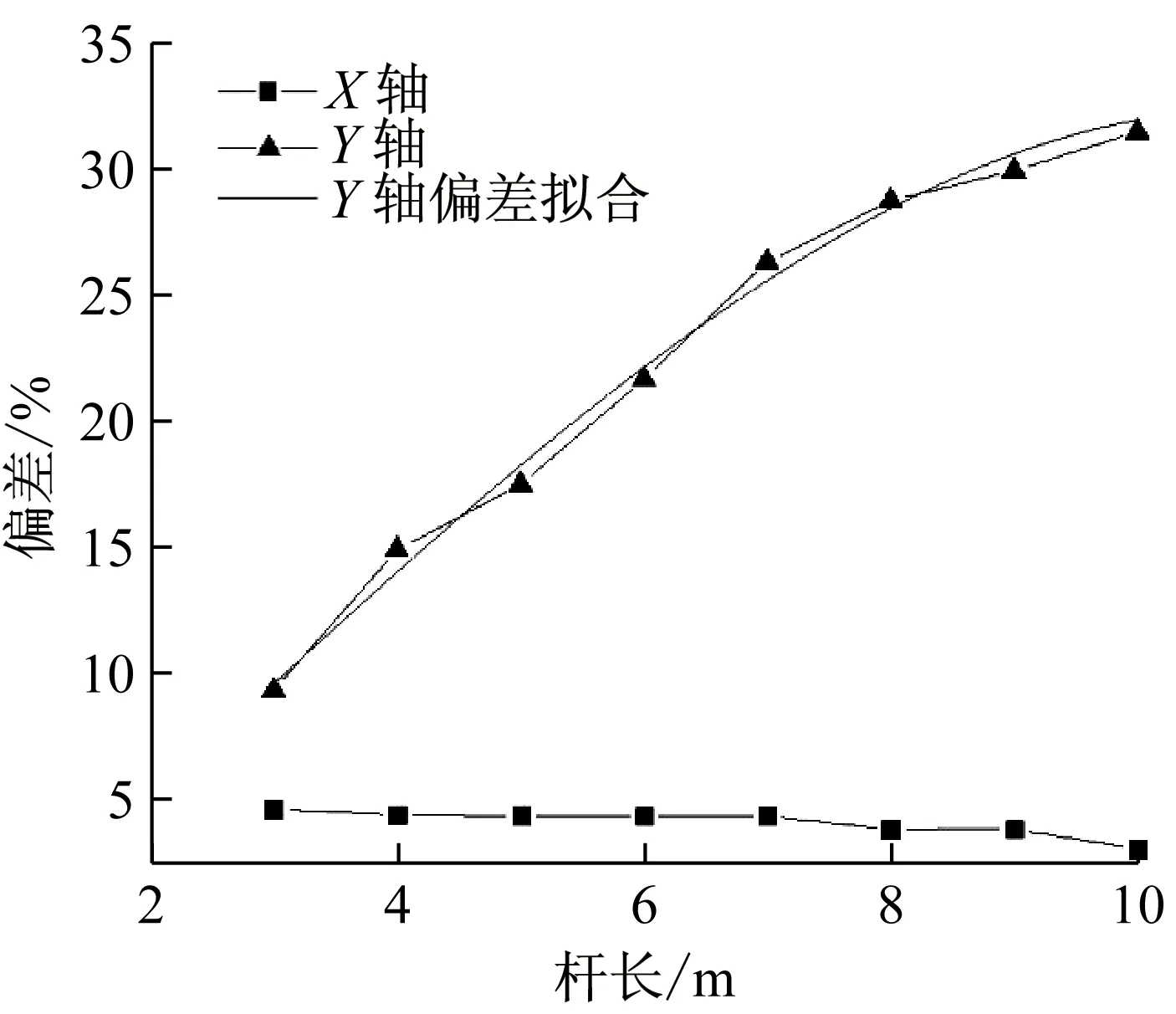
图15 不同杆长沿X轴向、Y轴向偏差值

4 结 论

本文对10 m超长薄壳结构CFRP豆荚杆进行了模态试验，得到了豆荚杆沿X轴向和Y轴向的频率；然后分别在考虑空气和不考虑空气影响的情况下进行了有限元数值计算；最后对豆荚杆的不同长度进行了参数化分析，可以得到以下结论：

(1) 对于本文试验研究对象，需要考虑空气与结构的耦合对结构频率模态的影响。

(2) 考虑豆荚杆独特的截面形状，空气对豆荚杆X轴向的影响较小，但对Y轴向频率的影响较大。

(3) 不同的豆荚杆长度，空气对豆荚杆沿Y轴向的频率影响的程度不一样，在试验过程中和实际工程应用中，要根据实际对象的不同，决定是否需要考虑空气对豆荚杆沿Y轴方向频率的影响。

[1] 陈务军.空间可展结构体系与分析导论[M].北京:中国宇航出版社,2006:1-50.

[2] 白江波,熊峻江,高军鹏,等.可折叠复合材料豆荚杆的制备与验证[J].航空学报,2011,32(7):1217-1223.

BAI Jiangbo, XIONG Junjiang, GAO Junpeng, et al. Fabrication and validation of collapsible composite lenticular tubes[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1217-1223.

[3] 房光强,彭福军.航天器可展开支撑杆的研制及其收拢展开特性研究[J].材料工程,2009(增刊2):157-160.

FANG Guangqiang, PENG Fujun. Fabrication and retraction/deployment testing of space deployable booms[J]. Journal of Material Engineering, 2009(Sup2): 157-160.

[4] 董志强,段宝岩．星载天线缠绕肋条的力学特性研究[J]．西安电子科技大学学报,2001,28(6):755-758.

DONG Zhiqiang, DUAN Baoyan. Study of the behavior mechanics of the extendible satellite antenna with the type of twinning ribs[J]. Journal of Xidian University, 2001, 28(6): 755-758.

[5] 李瑞雄,陈务军,付功义,等.透镜式缠绕肋压扁缠绕过程数值模拟分析[J].宇航学报,2011,32(1): 224-231.

LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation of flattening and wrapping process of lenticular wrapped-rib[J].Journal of Astronautics, 2011, 32(1): 224-231.

[6] 邹涛,陈务军,彭福军，等.透镜式缠绕肋收展过程数值模拟分析[J].哈尔滨工程大学学报,2013,34(2):151-156.

ZOU Tao, CHEN Wujun, PENG Fujun， et al. Numerical simulation of stowing and deploying process of lenticular wrapped-rib[J].Journal of Harbin Engineering University, 2013,34(2):151-156.

[7] 李瑞雄,陈务军,付功义.透镜式薄壁CFRP 管空间伸展臂轴压屈曲分析及试验[J].宇航学报,2012,33(8): 1164-1170.

LI Ruixiong, CHEN Wujun, FU Gongyi. Buckling analysis and experiment of lenticular CFRP thin-walled tube space boom under axial compression[J].Journal of Astronautics, 2012, 33(8):1164-1170.

[8] 李瑞雄,陈务军,付功义，等.透镜式缠绕肋压扁缠绕过程数值模拟及参数研究[J].工程力学,2011,28(11):244-250.

LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation and parametric study on flattening and wrapping process of lenticular wrapped-rib[J]. Engineering of Mechanics, 2011, 28(11):244-250.

[9] 刘锦贤. 空间可展天线支撑结构热-结构分析[D].上海:上海交通大学,2013.

[10] HERBECK L, LEIPOLD M, SICKINGER C, et al. Development and test of deployable ultra-lightweight CFRP-booms for a solar sail[C]//Spacecraft Structures, Materials and Mechanical Testing. 2001, 468: 107.

[11] SICKINGER C, HERBECK L, BREITBACH E. Structural engineering on deployable CFRP booms for a solar propelled sailcraft[J]. Acta Astronautica, 2006, 58(4): 185-196.

[12] IRWIN R J, VEEN J A V, BUCHNER-SANTOS E, et al. Low-mass deployable spacecraft booms[J]. AIAA Paper, 2010, 8926: 2010.

[13] CHU Z Y, LEI Y A. Design theory and dynamic analysis of a deployable boom[J]. Mechanism and Machine Theory, 2014, 71: 126-141.

[14] STRAUBEL M, BLOCK J, SINAPIUS M, et al. Deployable composite booms for various gossamer space structures[C]//52ndAIAA/asme/asce/ahs/asc Structures, Structural Dynamics, and Materials Conference. 2011.

[15] 李华峰. 空间结构数值风洞模拟与流固耦合风致响应[D].上海:上海交通大学,2008.

Modal tests and analysis for space thin-walled CFRP lenticular booms

KANG Xiongjian1, CHEN Wujun1, QIU Zhenyu1, YU Zhengyue2, XIE Chao3, CAO Zhengli3

(1. Space Structures Research Centre, Shanghai Jiao tong University, Shanghai 200030, China;2. Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China;3. Aerospace System Engineering Shanghai, Shanghai 201108, China)

When space thin-walled carbon fiber reinforced plastic (FRP) lenticular booms are working, they are in a cantilever state. In order to know their structural dynamic responses, a 10 m-long thin-walled CFRP lenticular boom with its bottom end fixed was tested to obtain its modal frequencies and modal shapes. The FE model of the boom was built with the FE software ADINA, it was used to perform numerical simulation without air and with air surrounding, respectively to gain its modal frequencies and modal shapes. The numerical simulation results were compared with those of modal tests. It was shown that for the fundamental frequency of the tested boom, the error between the calculation value and the tested one is 38.40% without air and 4.7% with air, so considering the influence of air is necessary; the effects of the boom length on its fundamental frequency is also analyzed; when the boom length is 3-10 m, the deviations between its fundamental frequency value without air and that with air are obtained. The results provided a reference for optimization design of space thin-walled CFRP lenticular booms.

space thin-walled CFRP lenticular boom; modal tests; fluid-structure interaction; numerical simulation

国家自然科学基金(11172180); 航天先进技术联合研究技术创新项目(USCAST2015-24)

2016-01-29 修改稿收到日期：2016-06-06

康雄建 男，硕士生，1991年生

陈务军 男，教授，博士生导师，1969年生

V214

A

10.13465/j.cnki.jvs.2017.15.032