基于Adaboost算法在葡萄酒酒品分类中的实际应用

罗士钧北京师范大学附属实验中学

基于Adaboost算法在葡萄酒酒品分类中的实际应用

罗士钧
北京师范大学附属实验中学

在我们的生活中，常常会把一定数目的物品按一定要求分类的问题。目前，Adaboost算法在分类算法十分成熟，得到广泛应用。本文就Adaboost算法在葡萄酒酒品分类中的实际应用展开研究。

Adaboost算法；朴素贝叶斯算法；Parzen窗估计；分类器

一、背景分析

在我们的生活中，常常会把一定数目的物品按一定要求分类的问题。目前，Adaboost算法在分类算法十分成熟，得到广泛应用。本文就Adaboost算法在葡萄酒酒品分类中的实际应用展开研究。我们依据已有的葡萄酒样本，通过让计算机学习这些样本，在这些样本之间总结规律，学习如何分类。最终使得当我们再次给它一瓶酒后，他可以以较高的准确率判断出这瓶酒更可能属于哪一种品质。

本算法需要的算法及原理：Adaboost算法，朴素贝叶斯算法，核方法，Parzen窗估计，Adaboost算法的弱分类器由朴素贝叶斯分类器组成，而贝叶斯公式用到的概率密度需要Parzen窗估计。下面分别对其分析。

二、Parzen窗估计

Parzen窗估计是一种概率密度估计的非参数方法，即非参数估计。

所谓非参数估计是指，已知样本所属的类别，但未知总体概率密度函数的形式，要求我们直接推断概率密度函数本身。也就是说，Parzen窗估计实际是一个学习过程。它负责由给定的n个样本生成随机变量的分布密度函数。

对于我们的葡萄酒样本来说，每个样本都包括这瓶酒的颜色，各种成分含量，酒精度，以及它的等级。（均由数字表示）

将它们对应于一个高维空间中的向量x。有了这些样本，我们希望在这些样本里找到一定的分布规律。由于我们想知道未知的那瓶酒是哪一类的概率大，也就是希望知道它是每一类的概率分别是多少，即我们要求出样本每一点的概率密度。

基本操作就是：以空间每个点中心，构造一个超立方体小舱，其中超立方体小舱的棱长hn是由样本总数N确定的。采用滑动小舱估计每一点的概率密度。

定义单位方舱函数

此时，小舱内包含的样本数

依据概率密度P（x）的基本公式：

P（x）=（kn/N）/VN

kn代表区域内样本数，N为样本总数，VN代表区域内的体积。可以简单地这样理解，kn/N为概率，再除以“体积”就成了概率密度了。

三、朴素贝叶斯算法

首先来看贝叶斯公式

设A和B是两个事件，根据全概率公式：

我们用具体的例子来解释一下这个贝叶斯公式是怎么用的。对于一瓶测试酒，设事件A为这瓶酒的酒精含量小于20%，事件B为这瓶酒属于6等酒。假设有一个葡萄酒厂，P（A）=1/4表示这个酒厂生产的酒有20%酒精含量小于有1/4。P（B）=1/10表示生产的酒有1/10是属于6等酒。P（A|B）=1/3表示一瓶6等酒的酒精含量小于20%的概率是1/3。有这些数据，并由贝叶斯公式就可以得出P（B|A）=P（A|B）*P（B）*/P（A）=（1/3*1/10）/（1/4）=2/ 15。这表示一瓶酒精含量小于20%的测试酒是属于6等酒的概率是2/15。

由上面这个例子，我们小结一下：

设X表示一个葡萄酒样本，Y是这个样本的类别，分类问题就是在知道X的情况下计算Y

对于葡萄酒来说，如果葡萄酒有9个等级，那么Y有9种Y1, Y2,...,Y9，也就是

公式的原理明白了，那么如何用这个公式求出这瓶测试酒应该属于哪一个类别呢？只需要分别计算贝叶斯公式中每个因子后按公式计算即可：

1、算P（Yi）：计算各个类别出现的概率。

2、算P（X|Yi）：计算每个独立特征在各分类中出现的条件概率。

3、代入贝叶斯公式：对于特定的特征输入，计算其相应属于特定分类的条件概率。

4、选择条件概率最大的类别作为该输入类别进行返回，说明这瓶测试酒最可能是哪一类的。

（由于在计算每个类别时，分母P（X）都是一样的，所以可以不用计算）。

P（Yi）就是样本中Yi这一类出现的概率，是相对好算的。而P（X|Yi）是十分难算的，因为X是一个高维向量，P（X|Yi）是个高维度的条件分布。朴素贝叶斯模型在此大胆假设：各特征相互独立，且地位相等。这样转而计算

P（X|Yi）=P（x1=a1,x2=a2,...,xn=an|Yi）=P（x1=a1|Yi）*P（x1= a1|Yi）*...*P（x1=a1|Yi）

也就是说，朴素贝叶斯算法提前假设特征之间相互独立，且同等重要。虽然这个假设在一些情况下不太适用，强行使用会降低准确率，但是这可以大大简化算法的复杂度这一点还是很诱人的。

四、Adaboost算法

1、初始化所有训练样例的权重，例如有N个样例，每个样例权重就是1/N。

2、for m=1,2,...,M（M事先给定，或者所有样本被正确分类后终止循环）。

对于第m轮训练，训练弱分类器Ym（X），使其最小化权重误差函数。

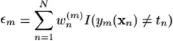
接下来计算该弱分类器的话语权α：

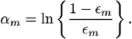
更新权重：

其中Zm是一个

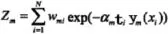
是规范化因子，使所有w的和为1。

3、得到最后的分类器

整个过程可以看出，自适应的具体体现在于：每一个分类器Ym（X）的分完类后会影响这个分类器在总分类器的话语权αm，同时“告诉”下一个分类器Ym+1（X）需要更加注重（通过增加权重）那些被分错的样本，相应地，被正确分类的样本的权重就被降低了。

五、结果分析

经过实际数据处理测试，此算法表现出正确率达到97.98%。数据来自http∶//archive.ics.uci.edu/ml/。

[1]蒋良孝.朴素贝叶斯分类器及其改进算法研究.（Doctoral dissertation,中国地质大学（武汉）），2009

[2]王国才.朴素贝叶斯分类器的研究与应用.（Doctoral disser⁃tation,重庆交通大学），2010

[3]曹莹,苗启广,刘家辰,&高琳.Adaboost算法研究进展与展望.自动化学报,2013，39（6）,745-758.

[4]李亚军,刘晓霞,&陈平.改进的adaboost算法与svm的组合分类器.计算机工程与应用,2008，44（32）,140-142.

[5]摆玉龙,&杨志民.基于parzen窗法的贝叶斯参数估计.计算机工程与应用,2007，43（7）,55-58.

罗士钧，现就读于北京师范大学附属实验中学高三年级。爱好数学，从小喜欢各种数学书籍、科普读物，有时喜欢看一些数学史、有趣的数学问题，与生活密切相关的数学定理等。中学开始学习数学竞赛和信息学竞赛，获得两次全国高中数学联赛二等奖。有时会对平时遇到的数学问题进行推广、思考、延伸。对于某一个数学问题，它常常会让我思考它的深层次的原理，和它的应用价值。