混合运算整理与复习教学研究报告

一、问题

混合运算是人教版数学教材二年级下册的内容，是学生系统掌握简单的整数四则混合运算（两步）的重要单元，其中，确定运算顺序是进行混合运算的关键。在此之前，学生已经会计算连加、连减、加减混合以及乘加、乘减的两步计算题，并且知道了小括号的作用。学生在四年级下册的四则运算单元中将继续学习相关内容。

1.教学实践中的问题

在教学实践中，二年级的老师普遍反映本单元基本计算不难，班上也只有个别学生的掌握情况不佳。而四年级的老师则强调班上仍有部分学生对运算顺序理解有误，计算时频频出错。为了进一步了解学生对混合运算的掌握情况，我们数学组分别对二年级156名、四年级49名学生进行了测试。测试的结果具体如下。

（1）运算顺序错误。

二年级测试卷共14道计算题，其中无小括号的两步混合运算题有8道。参与测试的二年级156名学生中，仅6人在有小括号的混合运算题上出错，但有57人在无小括号的计算题上出错。这57人中，错1～3个的有53人，错4～5个的有4人，错误人数约占测试人数的36.5%。

四年级测试卷共20道计算题，其中无小括号的混合运算题有16道。参与测试的四年级49名学生中，没有人在有小括号的计算题上出错，却有13人在无小括号的计算题上出错。这13人中，错1～4个的有10人，错11～15个的有3人，错误人数约占测试人数的26.5%。

（2）书写格式错误。

该问题主要出现在二年级学生中，错误人数占测试人数的14.22%。四年级学生没有出现该错误。

从以上测试结果来看，无论是二年级还是四年级的学生，对有小括号的混合运算掌握得较好，而受从左往右计算的思维习惯影响，在计算无小括号的二级混合运算题（例如60-40÷5）时出错率高。同时，二年级一部分学生会犯书写格式的错误，而四年级则没有学生再犯这个错误，说明随着学生年龄及认知水平的提高，此类错误将逐步消除。因此，我们认为，教师在教学混合运算整理与复习时，应重点关注运算顺序的落实。

2.教学策略

基于上述对教学内容的调研分析，我们将本节复习课的重点确定为对混合运算顺序，特别是无小括号的二级混合运算顺序的复习巩固。为此，我们将在复习课上做出以下几方面的尝试。

（1）设计分类活动，加深对计算法则的理解。

根据前测结果可知，学生在计算无小括号的两步计算题时，因受从左往右经验的干扰，对混合运算法则理解不透彻、记忆模糊，时常出错。如何有效地解决这个问题呢？我们认为，教师对计算法则进行梳理总结，能促进学生对法则的理解，加深对法则的记忆。为此，复习课上，我们先让学生独立完成一定数量的混合运算题，然后进行集体评议，纠正错误。接着，引导学生根据运算顺序，对完成的计算题进行分类，进而共同归纳总结出两大类（有小括号、无小括号）、三小类（有小括号、无小括号的同级运算、无小括号的不同级运算）的运算类型，加深对法则的理解与记忆。

同时，考虑到仅通过分类活动，学生对法则的掌握程度可能不够，于是，我们另外出示一组脱式计算题，要求学生不计算，将式子进行归类，再次强化对法则的记忆和理解，实现知识的巩固与能力的提升。

（2）提炼运算步骤，实现计算自动化。

对于学生而言，完成一道混合运算题需要经历确定运算顺序、着手计算这两步。基础较好的學生在明晰运算顺序后，的确可以做到准确计算，不易出错。但学困生虽然知道运算顺序，却在计算混合运算题时容易出错，这说明学困生的意识与实际操作之间仍存在一定距离，尚未形成计算自动化的心理机制。所以，将运算步骤进行难点分解，为学生提供一套简洁好记、操作性强的运算步骤就显得尤为必要。因此，我们将以上运算步骤提炼为“一看（看清运算符号）、二画（确定先算什么并画上横线）、三算、四查（查运算顺序、查每步计算）”，并要求学生在做计算题时严格按照标准步骤走，帮助学生形成计算自动化。值得一提的是，有人做过研究表明，用画线这种有运算标记的方式表征运算顺序，对于聚焦学生注意力、帮助学生顺利计算有显著的促进作用。

二、实践

（一）设计分类活动，深化学生对计算法则的理解。

1.设计分类活动，梳理总结运算顺序，复习巩固计算法则。

教师在黑板上出示一组计算题，学生独立练习。

34-17+3 28+21÷7（64-40）÷8 64-40÷8

12÷3×212÷（3×2）18÷3×33+7×4

学生练习完后，师生一起检查，纠错。

师：刚才我们做了这么多题，现在回过头来看看这些题（指黑板），你能根据运算顺序把它们分分类吗？（请学生上台移动计算卡片进行分类）

学生将卡片分成三类，分别为：有小括号、无小括号中同级运算以及不同级运算。

师：（指含有小括号的两道算式）你能说一说为什么先把它们放在一起吗？

生1：因为它们都含有小括号。（师板书）

师：有小括号的怎么计算？

生2：有小括号的就要先计算小括号里面的。

师：那换言之，剩下的就都是无小括号的（板书），（指无小括号的同级运算）这些算式中，你看懂了他为什么这样分吗？

生3：因为它们都只有加减法或者只有乘除法。

生4：我们都按照从左往右的顺序来计算。（师板书：只有加减法或只有乘除法，从左往右算）

师：（指无小括号的不同级运算）这些又为什么放在一块儿？

生5：因为它们既有加减法又有乘除法。

生6：它们需要先算乘除，再算加减。（师板书：既有加减法又有乘除法，先乘除再加减）

师小结：我们刚才对这些算式进行了分类整理，发现有小括号的，要先算小括号里面的；没有小括号的，如果只有加减法或者只有乘除法，就按照从左往右的顺序计算；如果既有加减法又有乘除法，我们就先算乘除再算加减。

2.补充专项练习，巩固对运算顺序的理解，加深对计算法则的记忆。

课件出示题目：帮算式宝宝回家。

师：第一个算式宝宝回谁家？理由是什么？

生1：回第三个家。因为这里有除法也有加法，要先算除法。

师：第二个算式宝宝呢？为什么？

生2：回第一个家。因为它有小括号，要先算小括号里面的。

师：那第三个呢？

生3：回第二个家。只有加减法，要从左往右算。

师：后面的算式宝宝请你直接把它们送回家。

……

（二）将运算步骤进行难点分解，帮助学生实现计算自动化。

师：刚才我们做了不少题，也为算式宝宝们找到了家，你认为要保证混合运算题全部做对，有什么诀窍？

学生讨论后交流。

師小结：一看（看清运算符号）、二画（确定先算什么并画上横线）、三算、四查（查运算顺序、查每步计算）。相信有了这个法宝，你肯定能算得又对又快！有信心再次接受老师的挑战吗？

师：（出示8道脱式计算题）请你根据刚才我们总结的计算法宝，按照一看、二画、三算、四查的步骤，完成下面各题。

43-25+5（6+12）÷66+12÷68÷4×2

40-20÷54×9-84+5×724-4×2

三、讨论

1.复习课到底面向谁？该复习什么？

在混合运算的整理与复习课堂上，我们常看到老师们将如下问题（如图所示）引入课堂，并不惜耗费大量时间进行讲解。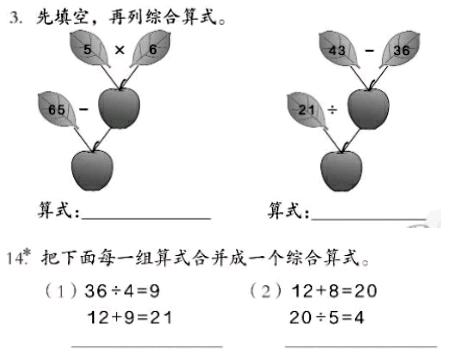

在我们看来，此种做法并不可取。这两道题均出自教材练习当中，综合性强、难度较大且并不重要。首先，它们并不关乎基本计算，对学生后续知识的学习影响不大；其次，在大部分老师看来，这两道题的出题目的是为学生列综合算式解决问题做好铺垫，但从实际学习效果来看并无多大帮助。我们在教学中发现，学生在面对具体情境时更易列出综合算式解决问题，而在这两道题中写出综合算式则表现得尤为困难。所以说，这两道题更多地是对做题者能力的考查、思维的挑战，就算学生此时不会，也不妨碍他们对核心知识的理解及后续学习目标的达成。

既然这两道题难度大且不重要，不应该成为复习课的教学重点，那么本节课的重点是什么呢？我们认为，教学重点应该是本单元的核心问题———混合运算的运算顺序。如果学生在此知识点上认识模糊，就会严重影响后续四年级乃至整个小学数学的学习。从前面的测试也可以看出，即便班上仅有几人没掌握到位，我们仍应自觉重视，力图面向全体学生，特别是学困生，达到人人掌握、个个落实的复习效果。

2.为何学生易在无小括号的二级混合运算顺序上出错？

我们先回顾学生有关混合运算的学习过程。学生一年级开始学习连加连减（如图所示）、加减混合运算（如图所示），知道了小括号的作用；二年级上册在乘法口诀单元接触了乘加、乘减模型（如图所示，均是乘法运算在前、加减法运算在后，如3×3+2、3×4-1，没有2+3×3这类）。从教材的编排顺序上，我们发现学生易在无小括号的二级混合运算顺序上出错的原因有以下几个。首先，由于小括号这一鲜明的符号刺激，学生很快就能接受“要先算小括号里面的”这一计算法则。其次，学生三次学习无小括号的二级混合运算时，皆是按照从左往右的顺序依次计算的，那么，学生就很可能陷入所有无小括号的混合运算都是按照从左往右的顺序进行计算的认知误区。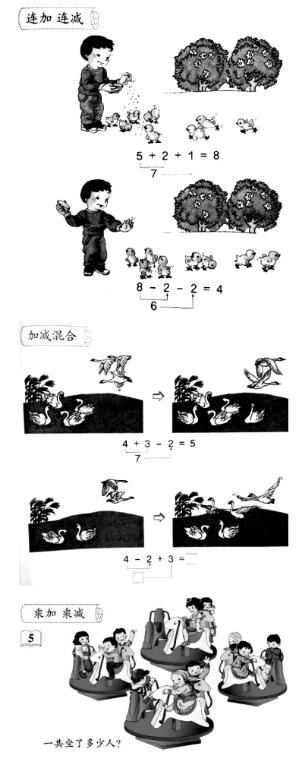

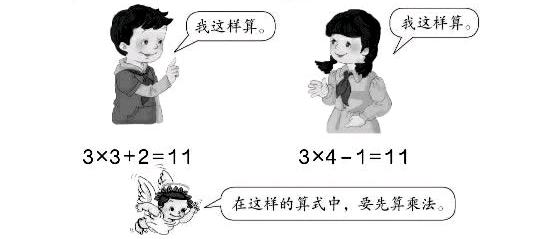
同时，参阅二年级下册第五单元混合运算的教材（如图所示）及教学参考书，我们发现在无小括号、不同级运算的例题教学中，教材试图借助现实情境，引导学生体会运算顺序的规定性，但对为什么这么规定、这么规定的合理性似乎并未给出一个科学的说法。这就导致教师在教学此内容时，很难向学生解释清楚运算顺序规定的合理性。学生也就未能够从意识层面真正理解并认可运算顺序的规定性，仅通过练习强化，难免会记忆模糊甚至遗忘。

因此对于本单元的复习课，我们在未充分给出合理解释的前提下，试图硬性转变学生的错误意识、纠正其错误认知，是有一定难度和挑战的。教师如何更科学有效地帮助学生建立运算顺序的正确观念，还需要进一步的探索和实践。

（执笔：李妍希、刘素芬、刘阳、肖英、朱秋菊、匡巧英、徐旺、李闯）